小学数学思维教学的几个案例（下）

三、“握手问题”的教学

正如人们广泛认识到的，抽象性可以被看成数学最基本的一个特性。例如，以下一些论述事实上都可以被看成关于数学这一特性的不同表述：“数学是模式的科学。”“数学抽象的思想是最基本的一个数学思想。”

从同一角度分析，这显然也可以被看成数学教学的关键，即我们在教学中应当很好地处理具体与抽象、特殊与一般之间的关系。后者不仅是指我们应通过诸多实例的分析帮助学生由特殊上升到一般，从而实现相应的抽象，也是指我们应以已建立的一般性认识为基础，更好地从事新的认识活动，包括已有认识的重构或深化，也就是通常说的由一般到特殊。

还应强调的是，尽管上面的论述似乎具有较强的理论性，但这事实上与我们的日常教学活动密切相关，我们应当联系自己的教学工作进行分析、理解，直至以此作为自觉的指导性原则。例如，通常所谓的“举三反一”与“举一反三”，可被看成关于由特殊到一般，再由一般到特殊的一个很好阐述。这也就如上海南洋模范中学的赵宪初先生所指出的：“数学教学需要‘举三反一，甚至有时需要‘举十反一，能够‘举三反一，孺子可教也。”当然，又如张奠宙先生所指出的，我们应“将‘举一反三和‘举三反一结合起来，使两者相辅相成”。因为，“学习者若能举一而反三、问一而知十，这必定是其熟悉内在道理并能融会贯通的结果。然而‘举一反三是建立在‘举三反一之上的，只有经过深入的三番考察、十方探究，总结得出一种客观规律（即‘举三反一），才能在应用该规律时做到‘举一反三”。（[3]第225页）

以下就依据相关论述对握手问题的教学做出具体分析，我们的论述将集中于这样一个问题：就这一内容的教学而言，有哪些方面直接涉及数学的抽象性，即由特殊向一般的过渡，以及再由一般到特殊？

首先，所说的问题在现实中往往会以多种不同的形式表现出来，如连线问题、单循环比赛场次的计算问题等。因此，这就是相关教学活动应当努力实现的一个目标，即不应满足于各个具体问题的解决，而应当从中抽象出普遍的数学模式。更一般地说，这事实上也就是诸多现实问题的教学中应当特别重视的一点。例如，就植树问题而言，相对于所谓的三种情况（即所谓的两端都种、只种一端和两端都不种）的区分而言，我们应更加重视如何以植树问题为原型抽象出普遍性的数学模式（可称为分隔问题），然后应用所说的模式解决各种类似的问题，如路灯问题、排队问题、锯树问题、爬楼问题等。当然，后者又以清楚地建立起这样一种认识作为必要的前提，即后面这些问题都与植树问题具有相同的数学结构，从而就可归结为同一个数学模式。（对此可见[1]第4.1节）

依据上述分析，相信读者可更好地欣赏以下的教学设计（[1]第一章，[例5]）：

老师：各位同学把桌子和椅子推开，空出中间的地方来，我们来玩握手游戏，每一组先找4个同学。

全班学生一起行动，很快就把桌椅推向两旁，然后很有默契地4个人组成一组，人数不够的，就找旁听者来充数。

老师：每两个人只能握手一次，不能重复。然后看看4个人握手能够握几次，把它记录下来。

每个学生都参与了这个工作。

老师：现在每一组换成5个人握手，看看能握几次。

学生很快换成5个人一组进行握手的活动。

老师：现在每一组6个人。

学生马上转变成6个人一组的形态。

活动结束，老师让学生回到各组，把刚才的记录画成表格，然后老师也在黑板上画出如下的表格，让学生发现其中的规律：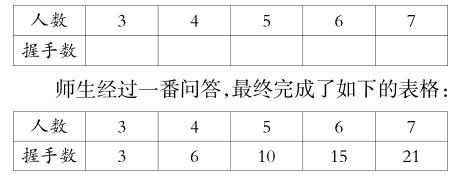

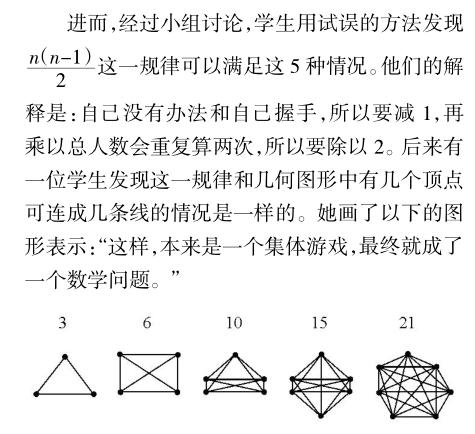
容易看出，这里所说的由课堂游戏向数学问题的转变，事实上也就是数学抽象的过程，即我们如何超越各个具体的事物或现象，揭示出一类具有相同数学结构的事物和现象的共同本质。

再者，在上述问题得到解决以后，我们还应注意引导学生对此做出进一步的推广，即对更一般的情况进行研究。

例如，就握手问题而言，我们不应局限于“每两个人握一次手”这样的情形，还应当就“每3个人组成一个小组”或“每4个人组成一个小组”等情况研究可能的组合数目。容易想到的是，如果采用更抽象的形式进行表述，这也就是所谓的组合问题———尽管后者已经超出了小学数学的范围，但在适当的条件下，我们仍可通过指明所说的发展帮助学生更好地理解数学家是如何进行工作的，包括由特殊到一般对于数学研究的特殊重要性。

另外，也只有从后一角度分析，我们才能更好地理解这样一个事实，即就握手问题而言，尽管我们可以通过综合分析引出相应的结论，即“自己没有办法和自己握手，所以要减1，再乘以总人数会重复算两次，所以要除以2”，但教学中采取以下做法则具有更加普遍的意义，即我们可以首先就总人数是3、4、5的情况分别引出相关的结论，然后通过归纳得出相应的普遍性结论。因为，除了后一做法可能更加适合学生的接受能力之外，显然还具有重要的方法论意义。而这事实上也可被看成数学抽象的又一重要表现：“对于一个特例，之所以要进行这样周密的描述，就是为了从中提出一般的方法或模式。这种模式，在以后类似的情况下，对读者求解问题可以起指引作用。”（[4]第一卷，第3页）

进而，从同一立场出发，相信读者也可更好地理解以下教学设计的意义，即在求解握手问题时，我们不是满足于通过具体实验去发现各种特殊条件下的相关结论，而是注意引导学生通过逐步的递归解决所面临的问题，也即致力于研究人数的增加与总的握手次数之间的关系。因为，这也是数学中经常用到的一个解题策略：“应当充分利用已获得的成果。”“在解题的每一阶段，我们都把關于一个新的分量的知识加到已经得到的知识上去，在每一阶段，我们又都要用已经得到的知识去得出更多的知识。”（[1]第4.1节。这方面的更多实例可参见书中第四章的[例2]和第三章的[例12]）另外，由所说的过程我们也可更好地理解如何实现由特殊向一般过渡这样一个建议：“通过系统的特殊化，为一般化提供直接的基础。”（梅森语）

四、“线段、射线与直线”的教学

这是笔者新近与广东省中山市小学数学教研员刘燕老师进行的一次讨论的直接主题，引发这一讨论的起因是她在一次教研活动中的以下发现。尽管这是关于线段、直线和射线的同课异构，几位执教老师却都是采取的从现实中寻找射线和直线的原型的方法，如用手电筒的光引出射线，用金箍棒引出直线等。尽管教师做出了很大的努力，相关的教学效果却似乎都不理想，如有不少学生认为金箍棒无论怎么延长，它上下总有两个圆圆的面；在将手电筒的光射向远处时，学生往往也会认为最后的结果是“光线看不见了”……

以下则是我们关于为何会出现上述现象的共同看法：这即可被看成十分清楚地表明了直观经验的局限性。具体地说，由于人们的实践活动始终停留于有限的范围，要想通过从现实生活中举例抽象、再返回现实生活寻找实际例子这一常用方法帮助学生理解射线和直线这样具有无限性质的概念是十分困难的。我们更无法通过实际操作对相关结论做出直接的检验。也正因为如此，这一教学活动的关键就在于，我们必须超出直观经验，让学生充分展开想象的翅膀。

刘燕老师依据这一思想做了一个新的教学方案，以下就是相关的部分。

1.认识射线

师：线段在生活中处处可见，它们都是直的，都有两个端点，一个是起点，一个是终点。可是数学家却通过想象创造了一种神奇的线，这种线也是直的，你猜，它有可能神奇在哪？

生：它只有起点，没有终点。

师：猜对了！闭眼想象一下，一条神奇的线，直的，只有起点，却没有终点……告诉我，你想象的这条线是什么样子的？

生1：它很长很长，长得望不到头。

生2：它长到宇宙中去了。

生3：它钻到地底去了，深得见不到底。

师：我们一起闭眼想象、比划一下这条线，想比划什么方向的？

生：横着的。

师：好，我们先来想象一条从左往右的。

师生（齐）：起点，唰……（师生边说边书空：从起点向右延伸）

师：到了终点吗？

生：没有。

师：到了终点吗？

生：没有。

师：找得到终点吗？

生：找不到。

师：让它继续飞，我们回来。

师：我们再一起闭眼想象一条竖着的。

师生（齐）：起点，唰……（师生边说边书空：从起点向上延伸）

师：到了终点吗？

生：没有。

师：找得到终点吗？

生：找不到。

师：你还想和它一起飞下去吗？

生：不想。

师：为什么？

生：没有终点，一直飞下去就回不来了！

师：还想比划一条什么方向的？

生：斜着的。

……

师：我们跟随数学家想象出来的这条线有什么特点？

生1：是直的。

生2：只有起点，没有终点，也就是只有一个端点。

生3：无限长，无法测量。

师：如果给这条线起个名字，你认为叫什么线？

生1：神线，因为没有终点。

生2：无限长线。

生3：射箭线，它像射箭一样射出去。

师：数学家和你想的一样，给它起了一个名字，就叫射线。（板书）

2.认识直线

师：射线已经够神奇了，可是数学家还通过想象创造出了一种更神奇的线，这种线也是直的，你猜，它又神奇在哪？

生：它连起点都没有了，没有起点，也没有终点。

师：猜对了！闭眼想象一下，一条神奇的线，直的，没有起点，也没有终点……告诉我，你想象的这条线是什么样子的？

生1：它很长很长，往上钻到云里面去了，往下钻到地底下了。

生2：我想象的是斜着的，起点和终点都没有，两边望不到头。

生3：我想象的是向左右两边伸展的，彩虹色的。

师：我们一起闭眼想象、比划一下这条线，先想比划什么方向的？

生：横着的。

师：好，我们先闭眼想象一条横着的，唰……向左看看，看到了起点吗？

生：没有。

师：向右看看，看到了终点吗？

生：没有。

师：还想比划什么方向的？

师：我们再一起闭眼想象、比划一条竖着的。唰……向上看看，看到了起点吗？

生：没有。

师：向下看看，看到了终点吗？

生：没有。

师：还想比划什么方向的？

……

师：这条更神奇的线有什么特点？

生1：是直的。

生2：没有起点，也没有终点，一个端点也没有。

生3：无限长，无法测量。

师：如果给这条线起个名字，你认为叫什么线？

生1：长又长线，因为没有起点也没有终点。

生2：双射线，它向两边延伸出去。

师：你们的创造力真强，想得很有道理，不过这次数学家不如你们，数学家给这条神奇的线起了一个非常非常普通的名字———直线。（板书）

在实践中，这一设计取得了较好的教学效果（这方面的又一课例可见[1]：第八章，[例14]）。以下则是笔者在进一步的讨论中所提及的几个建议。

第一，对于数学中所说的直线与生活中所说的直线，我们应当做出更清晰的区分，特别是，它们更可被看成构成了两个不同的范畴：（1）数学中的直线（射线）与线段；（2）生活中的直线（直的线）与曲线。

对于直线（射线）与线段的区分，我们可概括如下：如果说线段同时具有长度和方向这样两个属性，那么，对于直线和射线而言，前一概念已不再适用。这也就是指，方向是它们的唯一属性（显然，按照这一分析，平行线概念的引入也就十分自然了）。另外，我们事实上也可从同一角度对直的线与曲线的区分做出概括：与前者不同，后者仅仅具有长度这样一个属性。

第二，就射線与直线的理解而言，除了以数轴，即以自然数为例进行分析以外，还可提及时间的无限性，特别是后者的以下特点：它既没有终点也没有起点。

更深入地说，这两个例子与其说有助于我们更好地理解直线与射线这样两个概念，不如说正是直线与射线这两个概念为我们理解自然数与时间的无限性提供了必要的形象工具。

第三，也正是从后一角度分析，我们可很好地理解这样一个论述：“如果‘无限的直线这一概念的发明可以归功于某一个人的话，那么这位发明家就可自豪地说，‘我根据能摸、能扔、能摘的许多具体物体完成了这样一个自觉的思维过程。我的后代将因为我想象出了无限的直线而感谢我，因为借助这样的直线去认识世界，将比没有它要方便得多！”（[5]第85页）

更为一般地说，这也就是指，正是数学为人们更好地认识世界和从事实践活动提供了必要的概念工具。

最后，还应强调的是，这一例子事实上也可被看成通过发现问题、解决问题进行教学研究的很好实例。特别是，就只有坚持这样一个立场，我们才能在帮助学生学会数学地思维上取得切实的进展。

（作者单位：南京大学哲学系）

参考文献

[1]郑毓信.小学数学教育的理论与实践———小学数学教学180例[M].上海：华东师范大学出版社，2017.

[2]郑毓信.中国数学教育的问题特色[J].数学教育学报，2018年第1期.

[3]张奠宙.张奠宙数学教育随想录[M].上海：华东师范大学出版社，2013.

[4]波利亚.数学的发现[M].呼和浩特：内蒙古人民出版社，1980.

[5]郑毓信.数学方法论入门[M].杭州：浙江教育出版社，2006.