基于双指数模型的温度补偿系统设计

刘一兵， 李荣宽， 沈泓翔

0 引 言

微机电系统(micro-electro-mechancical systems,MEMS) 加速度计由于元件的内部结构、制造工艺以及工作环境等几方面的原因，存在测量输出误差。其中温度更是影响微机械加速度计可靠性和精度的关键因素。近几年国内外对温度补偿的研究，主要有模拟硬件设计和数字信号处理两种方法。模拟硬件通常采用与绝对温度成正比(proportio-nal to absolute temperature,PTAT)[1]和与绝对温度成正比(CTAT)[2]等技术设计读出电路，不过存在精度不高且需要反复调试的局限性；数字信号处理方法[3～5]大部分仅限于理论研究且不易集成到芯片中。

本文设计了一种易于工程实现的基于双指数模型的温度补偿系统。该系统一方面采用交替迭代法求解双指数模型的系数，另一方面采用硬件描述语言对扩展收敛域的坐标旋转数字计算(coordinate rotation digital computation,CORDIC)算法进行定点化建模，使得硬件实现变得更为方便，易于集成，因此,具有较强的工程实用价值。

1 温度补偿系统设计整体方案

温度补偿系统方案框架如图1所示。首先对含有温度传感器的MEMS加速度计进行零位温循环实验，得到零位电压输出Vout(V)和温度输出Vtemp(V)，通过模/数转换模块得到二者的数字量DigitalVout(V)和DigitalVtemp(V)。微处理器或计算机将数字量进行预处理并将数据点拟合得到双指数模型的系数存于数字补偿电路模块的ROM中。

最后在数字补偿电路中对加速度计的零位输出进行温度补偿。该温度补偿系统有以下优点：1) 采用硬件描述语言设计，易于集成到加速度计中;2) 将拟合系数存于ROM中，加速度计在任何状态工作时只需将温度信号作为数字补偿电路的输入，即可得到该温度下的补偿值，直接补偿加速度计输出信号;3) 指数函数可以通过CORDIC算法实现，使得数字补偿电路的实现变得更为简单方便，大幅提升了工程实用性。

图1 温度补偿系统框架

2 双指数模型交替迭代算法

双指数函数模型[6]为

Vout=α1eβ1Vtemp+α2eβ2Vtemp

(1)

式中Vout为加速度计的零位电压输出，V；Vtemp为加速度计中温度传感器的输出，V，表示温度值；α1和α2为线性拟合系数；β1和β2为非线性拟合系数。由于系数可以分为线性和非线性两类，使用交替迭代法[7]进行系数拟合。假设给点的数据点为{(Vouti,Vtempi)}，i= 1,2,…，n，算法具体步骤如下:

1)给出非线性拟合系数β1和β2的初值，记为β10和β20。

2)利用线性最小二乘法计算线性拟合系数α1和α2，其方程矩阵形式为

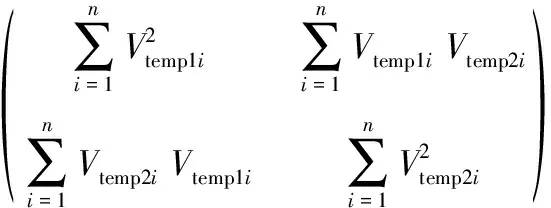
(2)

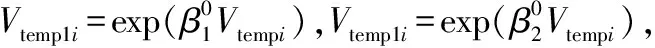
(3)

5)重复步骤(2)～步骤(4)，直到均方误差Δ满足给定的范围为止。

该交替迭代算法在一定程度上降低了初值的选取难度，使得计算效率提升。文献[8]提出的通伦交替迭代法可以进一步改善初值的依赖性问题。

3 扩展的指数函数CORDIC算法的定点化建模

3.1 指数函数CORDIC算法

在双曲坐标系下，指数函数CORDIC算法经过n次迭代后的输出方程为[9]

(4)

若选择初值X1=Y1=1/K，Zin=θ，有

Xn+1=Yn+1=coshZin+sinhZin=eθ

(5)

由于Zin的收敛范围较小，实际应用价值受到限制，所以必须扩大Zin的收敛域。

3.2 区间压缩的Zin收敛域扩张方法

若令Zin=Qln 2+θ0，其中Q∈Z表示Zin除以ln 2的整数部分，θ0表示Zin除以ln 2的余数部分。此时θ0小于ln 2一定在收敛域内，可以直接对其使用CORDIC算法计算

eZin=eQln 2+θ0=2Q×eθ0

(6)

式(6)中，若整数Q能够确定，则2Q可以通过左移或者右移|Q|位实现，从而可以把eZin的计算通过转化为对eθ0的计算，通过压缩区间的方式实现指数函数CORDIC算法的收敛域扩展[10]。

3.3 扩展的Q值和θ0值的定点化求解方法

文献[10]给出了Q值和θ0值的现场可编程门阵列(field programmable gate array,FPGA)求解方法。不过给出方法中输入值的范围为[-26,26)，定点化采用扩大216倍。在本节中，将该方法的输入值Zin范围扩展到[-2N,2N)，定点化扩展到扩大2M倍。因此,输入角度Zin和其整数Q值和小数θ0值定点化关系式为

Zin/ln2×2M=2M×(Q+θ0/ln 2)

(7)

图2为扩展的定点化求解整数部分Q和余数部分θ0的框架。第一个乘法器计算式(8)，integer表示向下取整，即计算出2M+N+3位的A并将后2M位定点化小数部分舍弃后得到整数部分Q值。第二个乘法器计算式(9)，demical_M表示取A的小数部分的前M位(A[2M-1︰M])，与扩大2M倍的ln 2相乘后得到余数部分θ0

integer[(Zin×2M)×(2M/ln2)]=2M×2M×Q

(8)

demical_M[(Zin×2M)×(2M/ln 2)]=2M×θ0/ln 2

(9)

通过上述分析和式(6)～式(9)可知，在采用定点化技术的CORDIC算法的收敛域扩展仅需2个乘法器即可实现输入Zin在任意范围内(-2N,2N)相对于ln 2的整数Q和定点化余数θ0的求解。并且为了满足实际需要，可选择任意定点化精度值。

图2 扩展的Q值和θ值定点化求解框架

4 仿真实验与分析

4.1 双指数函数拟合

对2只MEMS加速度计M1，M2进行实验和分析。为了定量分析双指数函数拟合的有效性，本文采用均方根误差(root mean square error,RMSE)和确定系数(R_square)作为评价指标来对双指数模型进行检验。图3为双指数模型对M1和M2温度曲线拟合的结果。

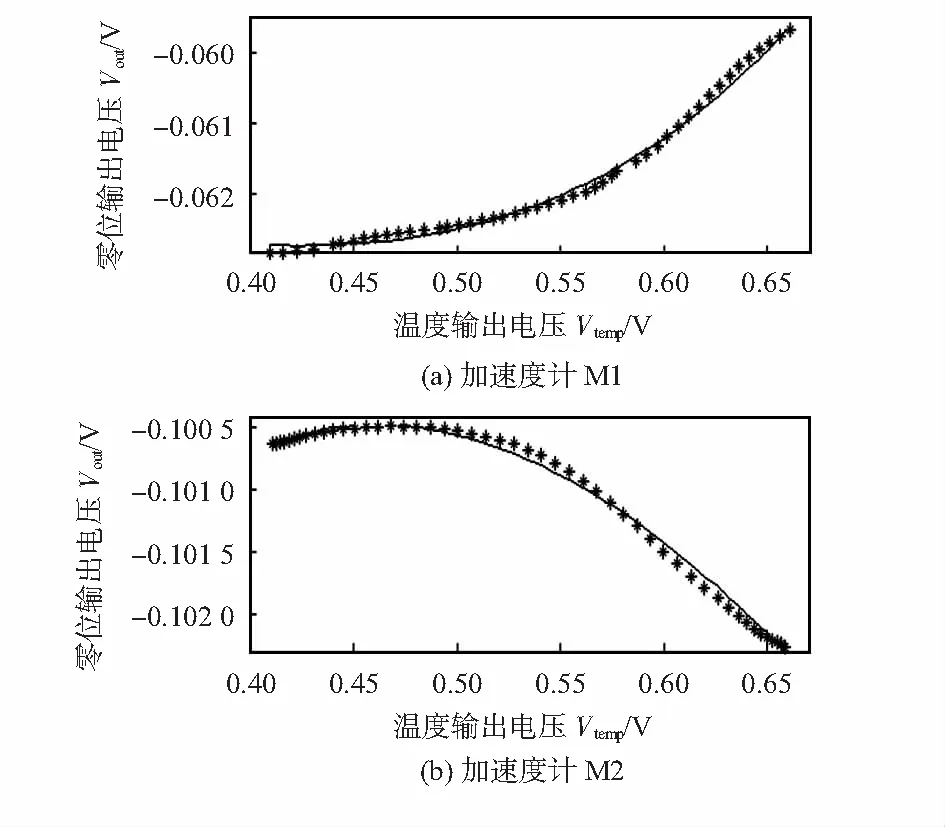
图3 2种加速度计温度曲线拟合效果

表1和表2为不同函数模型的拟合效果，其中序号1，2,3分别代表双指数函数模型、3阶多项式模型、4阶多项式模型。

M1,M2双指数模型表分别为

(10)

表1 M1型加速度计不同函数模型拟合效果

表2 M2型加速度计不同函数模型拟合效果

从图3和表1、表2可以得出，M1,M2型加速度计采用本文的双指数模型可以达到4阶及以上多项式拟合精度。

4.2 数字补偿电路仿真结果

数字补偿电路采用Verilog HDL语言进行建模。表3为采用M2模型的Modelsim仿真结果。其中定点化精度选择扩大了216倍。

表3 M2模型的Modelsim仿真结果

从表中可以看出，相对误差最大为0.019 %，可以满足实际工程上的精度要求，扩大定点化倍数可继续提升精度，因此,具有工程实用价值。

4.3 数字补偿电路补偿结果

图4所示为将2种MEMS加速度计的Modelsim仿真结果导入MATLAB中与原数据点进行补偿，并与补偿前数据进行对比。

图4 零位输出温度补偿结果

M1型温度曲线峰峰值从补偿前的0.003 9 V降到了3.687 1×10-4V；M2型从0.001 9 V降到了1.841 3×10-4V。实现了降低1个数量级的目标，可以看出，温度曲线有了较好的改善。由于双指数函数模型的对称性，整个数字电路模块由3个乘法器和1个流水线CORDIC算法模块组成，顶层计算时仅用实例化2次，并行运行相加即可。因此，在速度和面积上较4阶以上多项式更有优势。

5 结束语

基于现有温度补偿算法较为复杂，大部分仅限于理论研究的局限性，设计了一种基于双指数模型的易集成的温度补偿系统。补偿系统采用交替迭代法计算双指数模型系数，同时为了解决CORDIC算法计算指数函数输入角度收敛域较小的问题，采用区间压缩法扩展收敛域，并提出了一种扩展的定点化求解方法进行硬件模块设计，使得数字电路实现简单，易于集成到芯片中。根据实验可以看出：零位温漂减少了1个数量级，进一步提高了零偏稳定性，因此，具有很强的工程使用价值。

参考文献:

[1] Zhang C,Wu Q,Yin T,et al.A MEMS gyroscope readout circuit with temperature compensation[C]∥The 5th IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS),2010:458-462.

[2] Yin T,Wu H,Wu Q,et al.A TIA-based readout circuit with temperature compensation for MEMS capacitive gyroscope[C]∥IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS),2011:401-405.

[3] Xia D,Chen S,Wang S,et al.Microgyroscope temperature effects and compensation-control methods[J].International Journal of Sensors，2009,9(10):8349-8376.

[4] Ji X,Wang S,Xu Y,et al.Application of the digital signal procession in the MEMS gyroscope de-drift[C]∥The 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems,NEMS’06,2006:218-221.

[5] Wu X,Duan L,Chen W.A Kalman filter approach based on random drift data of fiber-optic gyro[C]∥The 6th IEEE Conference on Industrial Electronics and Applications (ICIEA),2011:1933-1937.

[6] 韩 丹,江 春,付鹏涛,等.探测器信号波形离散序列的多项式与双指数曲线拟合及其在数字化核能谱中的应用[J].核电子学与探测技术,2010,30(8):1075-1078.

[7] 赵林明,习华勇.数据拟合方法程序设计及其应用[M].石家庄:河北科学技术出版社,2000:79-80.

[8] 陈 华,邓少贵,范宜仁.同伦交替迭代法在双指数拟合中的应用[J].计算机工程与应用,2007,43(25):204-205.

[9] 周晓青，李合生，陶荣辉，等.基于 CORDIC 算法的双曲正余弦函数 FPGA实现[J].信息与电子工程,2010,8(2):211-214.

[10] 唐文明,刘桂雄.指数函数 CORDIC 算法的 FPGA 定点化技术[J].华南理工大学学报：自然科学版,2016,44(7):9-14.