超空泡航行体操纵过程流体动力特性数值模拟研究

周景军，赵京丽，项庆睿

（中国船舶重工集团公司第七〇五研究所，西安 710075）

0 引 言

通气超空泡减阻技术是目前唯一一种能够大幅降低水下航行体阻力的减阻手段，“暴风雪”鱼雷的问世证明了该项减阻技术潜在的军事应用价值。超空泡航行体在水中运动过程中，前端空化器与水接触，产生部分升力，航行体尾部与空泡壁面发生相互作用进入滑水状态，航行体重力由前端空化器提供的升力，尾部滑行力以及尾舵提供的升力平衡，前端的空化器以及尾部的十字舵成为其主要控制部件[1-3]。空泡的存在使航行体的流体动力与常规水下航行体相比有了明显区别。从公开发表的文章看，目前有关流体动力的研究工作主要针对攻角、舵角固定条件下的定常及非定常水动力。其中，文献[3]利用水洞试验对不同的超空泡形态下航行体尾部阻力系数、升力系数及俯仰力矩系数的变化规律进行了研究，并对航行体有无攻角情况下的尾部流体特性进行了比较，获得了攻角对尾部流体动力特性的影响规律。文献[4]在重力直流式水洞中对模型进行了一系列的试验，研究了轴对称体在通气空化下从局部空泡发展到超空泡状态过程中对水动力的影响。文献[5-6]在空化水洞中研究了不同攻角下，不同空化数和雷诺数条件下的空泡流特性，并对模型表面压力进行了测量，记录了空泡形态特性，最终获得了不同攻角下的航行体升、阻力系数曲线。文献[7]采用数值模拟方法研究了不同外形空化器在不同偏转角条件下的升力、阻力特性。另外，在超空泡航行体动力学建模方面，有关尾部滑行力的计算，主要采用经验公式进行计算[8-10]，这种方法要求明确给出空泡外形和沾湿区域空泡边界与模型间的夹角，其计算精度目前还未有定论。有关超空泡航行体操舵过程及姿态变化过程中的瞬态流体动力特性目前还未见有研究成果报道。

本文采用数值模拟方法结合动网格技术，基于欧拉两流体模型和SST湍流模型，重点分析了超空泡航行体巡航阶段空化器、尾部水平舵、垂直舵操舵过程以及航行体姿态变化过程的瞬态流体动力特性。对深入研究超空泡航行体巡航阶段的雷体特性具有重要的工程意义。

1 数学模型

多相流模型采用两流体模型。两流体流模型分别求解每相的连续性方程、动量方程和能量方程。两相之间的作用通过相界面进行传递，通过不同的模型来考虑。

（1）连续性方程

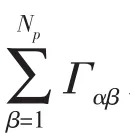
空化时的连续性方程为：

（2） 动量方程

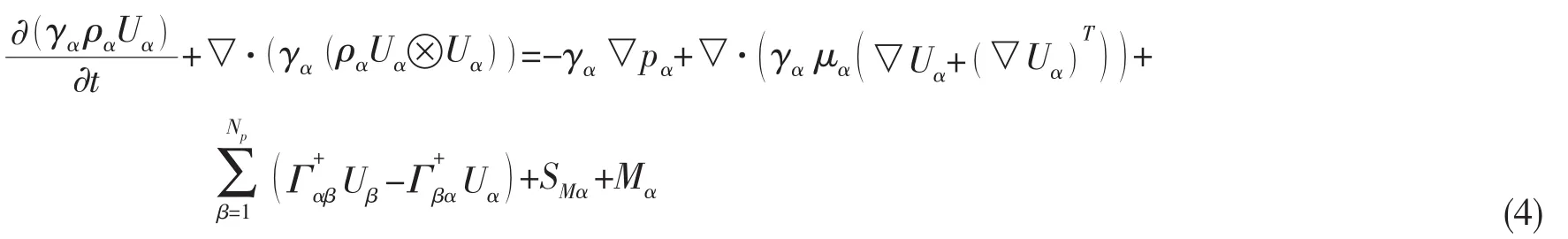
空化时的动量方程为：

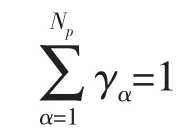
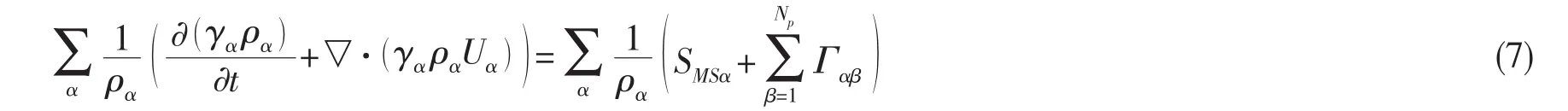
如果不考虑可压缩性以及忽略源相得：

（4） 压力约束

上述方程未知数共 5Np个（Uα，Vα，Wα，γα，pα），方程共 4Np+1，另外设各相压强为 pα=p，α=1，2，3,…，Np共Np-1个，一共5Np个方程，方程组闭合。

2 物理模型及计算条件说明

本文计算的模型如图1所示，具体几何尺寸如表1所示。其中尾舵采用三角翼型。模型长细比为15。其中模型总长2.8 m，直径为200 mm，空化器直径为40 mm。采用的网格如图2所示，全部采用结构化网格，网格单元数量为387万。

图1 航行体模型及网格Fig.1 The vehicle and the meshes

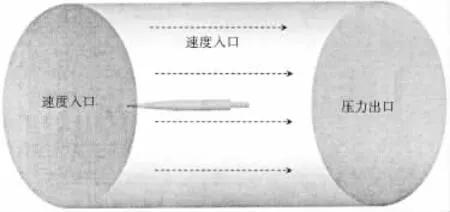
图2 边界条件示意图Fig.2 The sketch map of boundary conditions

2.1 边界条件说明

边界条件示意图如图2所示，其中来流方向前端及侧面均采用统一的速度入口边界，航行体尾部采用压力出口边界。流域直径为模型直径的10倍。流域总长为模型长度的4倍，其中模型前端距离速度入口等于模型总长，后部为模型总长的2倍。

2.2 操舵过程说明

操舵过程中，舵轴如图3所示。空化器舵轴中心位于空化器前端面圆心位置，尾部舵轴位于舵截面三角形心。

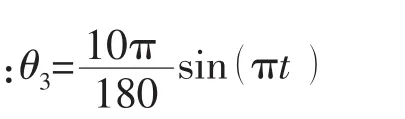
非定常计算时间步长0.001 s，每时间步迭代计算20次。

图3 操舵过程坐标系示意图Fig.3 The sketch map of coordinate frame in the process of steering

3 计算结果及分析

3.1 空化器操舵过程空泡形态及流体动力特性分析

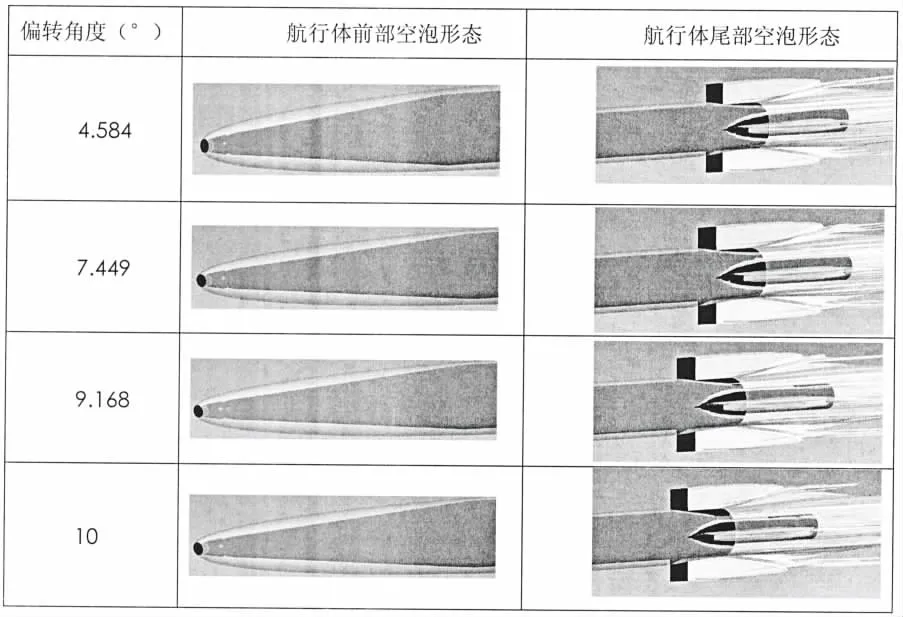
图4 空化器操舵过程空泡形态Fig.4 Cavity shape in the steering process of the cavitator

图5 空化器操舵过程空化器及航行体升力系数变化规律Fig.5 The change law of the lift coefficient for the cavitator sterring and vehicle

图6 空化器操舵过程航行体力矩系数变化规律Fig.6 Change law of torque coefficient during the steering of the cavitator

空化器操舵过程空泡形态如图4所示，空化器按照逆时针操舵过程，空泡形态发生变形，空泡向下变形，航行体尾部上端面沾湿面积变大。空化器操舵过程航行体流体动力特性如图5和图6所示，可以看出，空化器偏转过程，空化器上的流体动力随着空化器偏转角度的增加呈线形规律变化；航行体升力（主要包括航行体尾部和水平舵上的升力）基本上也呈线性规律变化，力矩导数数值大小约为0.000 38。

3.2 水平舵操舵过程空泡形态及流体动力特性分析

图7 水平舵操舵过程空泡形态Fig.7 The cavity shape during the steering of the horizontal rudder

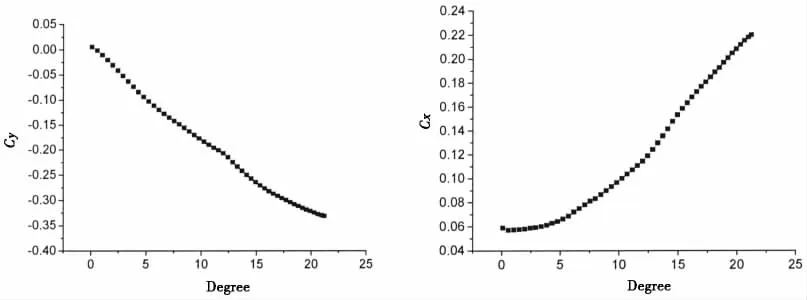
图8 水平舵操舵过程航行体升力及阻力系数变化规律Fig.8 The change law of lift and drag coefficient during the steering of the horizontal rudder

超空泡航行体水平舵操舵过程的空泡形态如图7所示，可以看出随着水平舵角的逐渐增加，航行体尾部沾湿面积发生明显变化，航行体尾部上部沾湿面积逐渐增加，其原因是由于舵角的变化导致航行体尾部流线发生明显弯曲，说明当水平舵面积较大时，水平舵操舵过程不但影响舵本身的流场，对航行体尾部流场影响同样不可忽略。结合图8和图9的流体动力变化规律可以看出，当空泡进入巡航阶段空泡相对稳定后，水平舵上的流体动力相对稳定，操舵过程中的流体动力变化规律基本上呈线形规律变化，对于本文中的航行体线形，水平舵操舵过程升力系数大约为0.015，远远大于空化器操舵过程中的升力系数。

3.3 垂直舵操舵过程空泡形态及流体动力特性分析

图9 水平舵操舵过程航行体力矩系数变化规律Fig.9 The change law of torque coefficient during the steering of the horizontal rudder

图10 垂直舵操舵过程空泡形态Fig.10 The cavity shape during the steering of the vertical rudder

图11 垂直舵操舵过程航行体力矩及侧向力系数变化规律Fig.11 The change rule of torque and lateral force coefficient of vehicle during the steering of the vertical rudder

超空泡航行体的垂直舵主要起横滚控制作用，因此流体动力参数主要体现在横滚力矩系数和侧向力系数。从图10中的空泡形态可以看出，垂直舵操舵时对于空泡形态的影响和垂直舵类似，但是由于重力效应或者航行体姿态角的影响，垂直舵上下舵的沾湿面积不同，垂直舵操舵过程对于航行体表面的沾湿区域影响同样明显。流体动力方面，由图11可以看出，横滚力矩随着差动舵角的增加基本上呈线性规律变化，由于舵沾湿面积的不同以及差动舵对与航行体本身的沾湿区域的影响，差动舵操舵过程，侧向力大小不可忽略，随着差动舵角的增加，侧向力同样呈线性规律变化。

3.4 航行体攻角变化过程空泡形态及流体动力特性分析

图12 航行体攻角变化过程空泡形态Fig.12 The cavity shape for the different attack angle of vehicle

超空泡航行体进入巡航段后，尾部滑行力是其平衡力系中的重要分量。结合图12-14可以看出，随着航行体攻角的逐渐增加，航行体阻力系数、升力系数及力矩系数都发生规律性变化，其中升力系数和力矩系数变化率在攻角0.5度前大约为0.16，远大于由于水平舵和空化器操舵引起的升力系数变化规律，说明航行体攻角对于航行体升力系数的贡献占主导地位，同时在小角度变化范围内，基本上呈线性规律变化。另一方面，随着航行体攻角的变化，升力系数和力矩系数的变化率明显发生变化，升力系数变化率大约为0.33左右。当攻角大于0.7-0.8度时，航行体升力系数和力矩系数开始呈下降趋势。

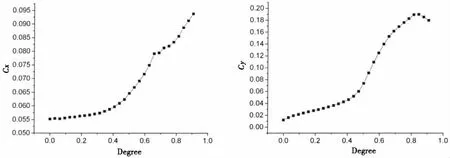
图13 航行体攻角变化过程中阻力系数和圆柱段升力系数变化规律Fig.13 The change rule of drag coefficient and cylinder lift coefficient for the different attack angle of vehicle

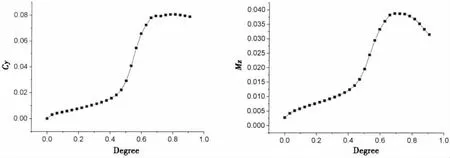
图14 航行体攻角变化过程中水平舵升力系数和航行体力矩系数变化规律Fig.14 The change rule of the lift coefficient of the horizontal rudder and the torque coefficient of vehicle for the different attack angle of vehicle

4 结 论

本文采用数值模拟方法结合动网格技术，基于欧拉两流体多相流动模型以及SST湍流模型，研究了超空泡航行体空化器操舵过程、水平舵、垂直舵操舵过程以及航行体姿态变化过程中的空泡形态和航行体流体动力变化规律。主要成果如下：

空化器操舵过程中，空化器上的流体动力非常稳定，随偏转角度呈线性规律变化，尾部滑行力同样呈线性规律变化；水平舵和差动舵操舵过程，当舵的面积相对较大时，操舵过程将对航行体沾湿面积产生重要影响，进而影响航行体圆柱段上的流体动力；航行体姿态变化过程中对流体动力（主要指升力系数、力矩系数）的影响在航行体整个动作过程中占主导地位，以升力系数为例，与水平舵上的升力相比，相差一个数量级，与空化器偏转对升力系数影响相比相差3个数量级。本文研究成果对于进一步开展超空泡航行体动力学特性分析具有重要意义。

[1]Savchenko Y N.Experimental investigation of supercavitating motion of bodies[C].VKI Special Course on Supercavitating Flows,Brussels:RTO-AVTand VKI,2001.RTO-EN-010(4).

[2]Savchenko Y N.Supercavitation problems and perspectives[C].Fourth International Symposium on Cavitation,California:California Institute of Technology,2001.lecture.003.

[3]佟力永.超空泡航行体楔形舵片流体动力学特性数值模拟[J].船舶力学,2015,19(7):765-773.Tong liyong.Numerical simulation on hydrodynamic characteristics of rudders of supercavitating vehicle on maneuvering condition[J].Journal of Ship Mechanics,2015,19(7):765-773.

[4]蒋增辉,于开平,张 嘉,王 聪,黄文虎.超空泡航行体尾部流体动力特性试验研究[J].工程力学,2008,25(3):26-30.Jiang Zenghui,Yu Kaiping,Zhang Jang,Wang cong,Huang Wenhu.Experimental research on hydrodynamic character of aft section of underwater supercavity bodies[J].Engineering Mechanics,2008,25(3):26-30.

[5]蒋洁明,鲁传敬,胡天群,程 鑫.轴对称体通气空泡的水动力试验研究[J].力学季刊,2004,25(4):450-456.Jiang Jieming,Lu Chuanjing,Hu Tianqun,Cheng Xin.The experimental research on the cavitating flow around an asisymmetric body with ventilation[J].Chinese Quarterly of Mechanics,2004,25(4):450-456.

[6]Ota T,Ueda K,Yoshikawa H.Hysteresis of flow around an elliptic cylinder in critical reynolds number regime[C]//ASME Heat Transfer/Fluids Engineering Summer Conference.Charlotte,North Carolina USA,2004:HT-FED04-56141.

[7]Ota T,Tsubura I,Yoshikawa H.Unsteady cavitating flow around an inclined rectangular cylinder[C]//ASME Heat Transfer/Fluids Engineering Summer Conference.Charlotte,North Carolina USA,2004:HT-FED04-56143.

[8]周景军,于开平.空化器倾斜角对超空泡流影响的三维数值仿真研究[J].船舶力学,2011,15(1):74-80.Zhou Jingjun,Yu Kaiping.Three dimensional numerical simulation on the influence of cavitator inclination angle to supercavity flow[J].Journal of Ship Mechanics,2011,15(1):74-80.

[9]颜 开,褚学森,许 晟,冯 光.超空泡流体动力学研究进展[J].船舶力学,2006,10(4):148-155.Yan Kai,Chu Xuesen,Xu Sheng,Feng Guang.Research progress of supercavitation hydrodynamics[J].Journal of Ship Mechanics,2006,10(4):148-155.

[10]冯 光,颜 开.超空泡航行体水下弹道的数值计算[J].船舶力学,2005,8(2):1-8.Feng Guang,Yan Kai.Numerical calculation of underwater trajectory of supercavitating bodies[J].Journal of Ship Mechanics,2005,8(2):1-8.

[11]Vasin A D,Paryshev E V.Immersion of cylinder in a fluid through a cylindrical free surface[J].Fluid Dynamics,2001,36(2):31-37.