对一道例题的反思
张 冰
(陕西省西安交大附中 陕西西安 710048)
在高中数学实验教材(北师大版)选修2-2《导数的几何意义》中介绍了一道例题,课堂上讲解这道题目之后,又有了很多想法和反思,现将课后对这道题目的反思记录下来,希望对今后的教学有所启发。
1.例:已知曲线
(1)求曲线在点处的切线方程;
(2)求曲线过点处的切线方程。
解:(1由曲线的几何意义,曲线在点处的切线的斜率是

所以曲线在点处的切线方程为:
即:
(2)曲线过点处的切线可能(1)P是切点;(2)P不是切点
当P是切点时,即第(1)小问的情形,曲线在点处的切线方程为:
当P不是切点时,假设切点为

这时曲线的切线方程为:
通过图像可以验证曲线过点P的曲线确实有两条。
课堂的例题分析、讲解是结束了,在课后回顾这道例题的时候,突然想到是否对任意的一条三次曲线,过曲线上任意一点都是有两条切线吗?
对于三次函数过曲线上任意一点作切线,切线的情形如何?
因为以点P为切点的切线一定存在,切点不是点P的切线是否一定存在?
假设切点由点Q在曲线上,
得:
又,点Q在切线上,切线PQ的斜率
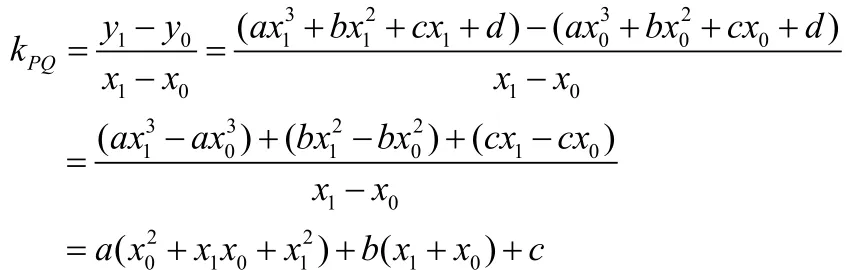
由导数的几何意义可得:
所以,
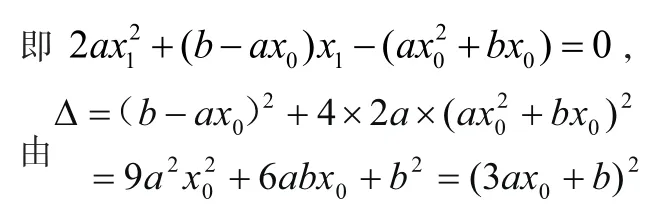
当时,点Q与点P重合,过点P有且只有一条切线;
当∆≠0,即时,过点P的切线有两条,切点分别是点P和点Q。
所以,如果,过点P的切线有且只有一条,否则有两条切线,切点分别是点P和点Q。另一方面,正好也是的对称轴,这样进行判断时就很容易了。
有什么特别的意义吗?
我们知道是以为中心的中心对称图形,也是中心对称图形吗?其对称中心又是什么呢?
设函数的对称中心为
按向量将函数的图像平移,则所得函数是奇函数。
所以
化简得:
上式对恒成立,有
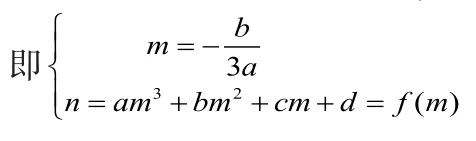
以上证明告诉我们:函数是中心对称图形,其对称中心为:
,该点在其导函数:
的对称轴上。
从对这道例题的反思中让我更加体会到了教学的乐趣,一天的课下来,在无人的时候,翻着自己的教案,重温课上的每一个细节,什么地方精彩,什么地方失败,哪一句话引起了学生的共鸣,什么地方调动了学生的积极性,再对教案进行更进一步的修改,同时记录下课上的一些突发奇想,某个灵感或突然间悟到的一种更好的调控课堂的方法,与学生沟通的方式等。时间一长,就发现自己对这些看似鸡毛蒜皮的课堂细节的总结,在不知不觉中形成了自己独特的教学风格。但细节每堂都有,总结每天进行,收获乐趣多多。

