复杂网络的度分布及其算法

王桂山 任学藻 西南科技大学 许凡 河南理工大学

自然界中存在的大量复杂系统都可以通过形形色色的网络加以描述一个典型的网络是由许多节点与连接两个节点之间的一些边组成的，其中节点用来代表真实系统中不同的个体，而边则用来表示个体之间的关系，通常是当两个节点之间具有某种特定的关系时连一条边，反之则不连边有边相连的两个节点在网络中被看作是相邻的。

一网络的发展大致经历了规则网络、随机网络和复杂网络三个阶段。

第一阶段规则网络的理论：图论的发展始于18世纪伟大的数学家Euler对著名的柯尼斯堡（konigsberg）七桥问题的研究。开创了数学分支图论的研究，研究表明规则网络具有较大的聚类系数和较大的平均最短路径长度，其所有的节点都有相同的度，节点度分布为

第二阶段随机网络阶段理论：如果节点之间不按确定的规则连接，而是以一定的概率随机连接，所得到的网络就是随机网络。20世纪60年代，两个著名的匈牙利数学家Erdo和Renyi提出的ER随机网络模型，开创了随机网络的研究的新局面。随机网络具有较小的聚类系数和较小的平均最短路径长度，节点度分布为泊松分布。

第三阶段复杂网络理论：在世纪之交，随着计算机技术的高度发展、计算机运算能力的不断提高，人们拥有了各种的数据库，因此对大规模的网络进行实证研究有了可能，复杂网络科学取得了突破性的进展。问题的起因可追溯到20世纪60年代，美国心理学家曾做过一个所谓‘六度分割’（six degree of separation）实验。已有的规则网络和ER随机网络都无法解释这种“小世界现象”。

1998年Watts和Strogata提出了小世界网络模型，说明了少量的随机捷径（Random shortcuts）会改变网络的拓扑结构，从而涌现出“小世界效应”，小世界网络模型介于规则网络和随机网络之间，具有较大的聚类系数和短平均路径长度，节点度分布为泊松分布，比规则网络和随机网络更能模拟真实网络的特性。

1999年的Barabasi和Albert在研究万维网时发现，万维网的度分布不像随机网络和小世界网络那种具有对称的泊松分布，而是偏倚的幂律分布，在该网络中，大多数节点仅有少量的连线，而少数节点拥有大量的连线。为此提出了无标度（Scale-free）网络模型，揭示了增长和择优机制在复杂网络自组织演化过程中的普遍性和幂律的重要性。无标度网络中的节点具有很强的异质性，不同度的节点在网络中的重要性不同。例如：在城市交通网络中，度分布表示城市之间的航线的多少和重要程度，度越大的城市，其重要性也越大；在社会网络中，度可以表示个体的作用力和影响度，一个节点的度越大，一般表示在整个网络中的作用和影响越大，反之亦然。

复杂网络可以描述自然界和人类社会中大量的复杂系统，一个典型的网络是有许多节点和一些连接节点间的边组成，其中节点代表真实系统中不同的个体，二边则表示个体之间的关系。例如上面提到的交通网络每个节点代表一个城市，每条边表示两个城市间有一条航线。目前复杂网络的研究主要为：社会网络、信息网络、技术网络、生物网络等。

复杂网络在社会网络中的应用十分广泛，社会网络是指社会个体成员之间因为互动而形成的相对稳定的关系体系，社会网络关注的是人们之间的互动和联系，社会互动影响到人们的社会行为。社会网络研究如个人间的朋友关系，公司商业伙伴关系，电影演员合作网络，性接触网络，科学家合作网络等。目前，复杂网络研究主题主要包括：复杂网络的拓扑性质，复杂网络的生成机制，复杂网络的演化的统计规律，复杂网络的结构稳定性，复杂网络上的传播机理与动力学特性，复杂网络中的搜索，复杂网络中的同步与控制以及把网络拓扑结构与具体系统结合起来。

分析复杂网路在随机和恶意攻击下的鲁棒性。对于随机网络而言网络中的节点是同质的，即网络中所有的节点几乎具有相同的度数。而无标度网络具有很强的异质性，网络中大部分节点具有较小的度只有少量的节点具有较大的度，当随机删除一小部分节点时，随机网络的直径随着删除节点的多少单调增加，而无标度网络的直径几乎不变。

度分布是复杂网络研究的一个重要的统计量，节点度数反映了节点在网络中的重要性，度数越大的节点在网络中有越多的邻居节点，它的变化对网络的影响越大，反之亦然。网络度分布描述了网络中节点度的分布情况，具有指数型度分布的网络中节点是同质的，这样的网络对恶意攻击具有很强的鲁棒性；具有幂律度分布的网路中节点是异质的，网络中大部分节点具有很小的度数，但也存在极少数量的节点度很大，这样的网络对于随机攻击具有强的韧鲁棒性，但对于恶意攻击却很脆弱，下面系统分析网络度分布的方法：

平均场方法：Barabasi等人分析BA模型的度分布提出了平均场方法（mean-fild approach）。具体计算步骤如下：令表示节点i(在第i时刻加入到网络的节点)在时刻 时的度数，对于BA模型，在t时刻网络共增加了m条连线，每条连线连接网络中的两个节点，此时网络中节点的度数之和.根据连续性理论，把看做连续动力学函数，则满足如下的动力学方程

上述方程有如下的解：由于计算网络的度分布需要随机选择一个节点，所以中的i必须看成随机变量，由于节点是随机选择的，因此i在所有节点中服从均匀分布，又初始网络中含有个节点，从而通过

可得：对k求导即可得到表示在时刻t度数为k的节点所占的比例：

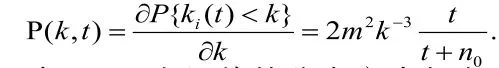
当时，网络的稳态度分布为：其中，为标度指数。

率方程方法：

Krapivsky等人在分析网络度分布的时候提出了率方程方法（rate-equation approach），求解过程：令表示在t时刻网络中度数为k的节点总数，对于BA模型根据连续性理论，现在考虑节点数的变化率，对于原来度数为的节点由于与新节点相连度数变为k，需要算入；对于原来度数为k的节点，由于增加了连线度数变为，需要排除；对于新节点，它的度数度数恰好为m，若k=m,则需要保留。节点i与新加入的节点相连的概率为可得到关于率方程由大数定律得结合上式可表示为：此方程式是一个关于一阶差分方程，解此方程可以得到:通过率方程方法得到BA模型的度分布服从指数为3的幂律分布，这个结果和平均场方法所得结果一致。

主方程方法：

Dorogovtsev等人提出了主方程方法（master-equation approach）.主方程方法求解度分布的步骤如下：对于固定的t,第i时刻加入到网络中的节点i的度数是一个随机变量，现在令对于BA模型，新节点加入到网络时选择旧节点i并与之相连的概率时得到下面的主方程：

这个方程的边界条件:对于BA模型，结合上式可以化简为：这是一个一阶差分方程，解此差分方程：

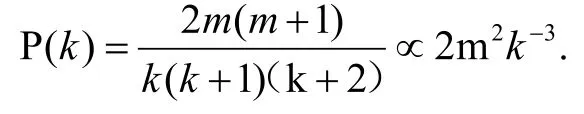
通过主方程方法可得BA模型是度分布服从指数为3的幂律分布的无标度网络。

鞅方法：

Bollobas等人用鞅方法严格证明了LCD模型度分布的存在性并求出了度分布的表达式，对于LCD模型，首先证明了当然后定义一个鞅

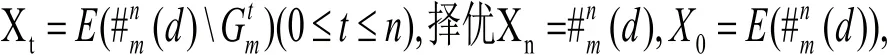
根据Azuma-Hoeffding不等式，对于每个d有:

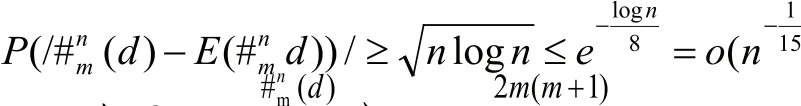
当时,有

BA模型的度分布另外一个求解方法，具体思路如下：首先令然后证明定义得

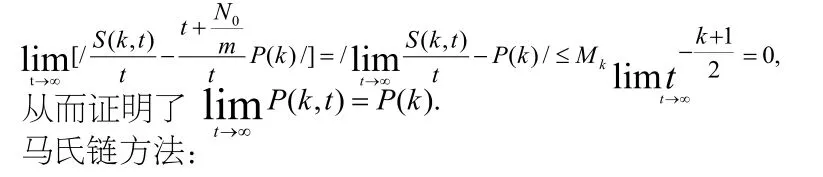
在BA模型中，对于每一个固定的t为一个随机变量，对于变动的t为一非齐次马氏链，马氏链的状态转移概率为

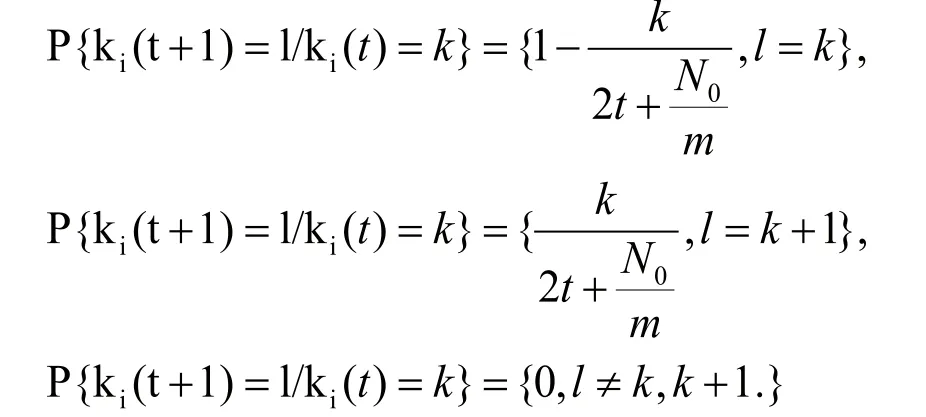
应用马氏链理论的首达概率及其方法和技巧，对节点度分布得出如下

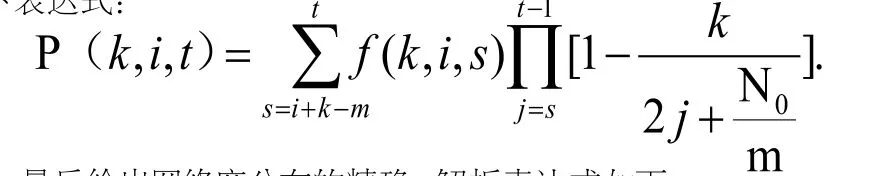
最后给出网络度分布的精确、解析表达式如下：

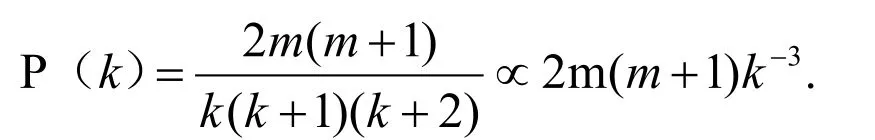
本文章马氏链方法在求解复杂网络度分布中，具有很好的普适性，对增长网络和演化网络的度分布进行了系统的分析，在对增长网络和演化网络的度分布问题给出了较为统一的答案。

[1]李彦.复杂网络研究概述[J].科学与财富,2012(10):35-35.

[2]叶笛.基于复杂网络视角的供应链网络研究[J].现代管理科学,2011(8):111-113.

[3]赵京胜,孙宇航.基于复杂网络理论的校友网络研究[J].信息技术与信息化,2014(2):121-126.

[4]庄天舒.基于复杂网络理论的Internet拓扑节点特征分析[J].长春大学学报,2010, 20(10):30-32.

[5]赵山春.基于复杂网络理论的城市公交网络可靠性研究[J].中国安全科学学报,2013, 23(4):108-112.

[6]胡海波.复杂网络拓扑结构的研究[D]. 西安理工大学, 2006.

[7]姚红光,朱丽萍.基于仿真分析的中国航空网络鲁棒性研究[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(1):42-46.

[8]蒋国平,宋玉蓉,巩永旺.基于复杂网络结构特征的病毒传播研究综述[J]. 南京邮电大学学报(自然科学版), 2012, 32(5):1-6.

[9]黄玮强,姚爽, 庄新田.基于复杂社会网络的创新扩散多智能体仿真研究[J].科学学研究,2013, 31(2):310-320.

[10]王甲生,吴晓平,陈永强，加权无标度网络级联抗毁性研究[J]. 复杂系统与复杂性科学, 2013,10(2):13-19.