基于自适应强跟踪CQKF的目标跟踪算法

刘畅， 杨锁昌,*， 汪连栋， 张宽桥

(1. 军械工程学院 导弹工程系, 石家庄 050000； 2. 电子信息系统复杂电磁环境效应国家重点实验室, 洛阳 471003)

目标跟踪是一类典型的非线性滤波问题，贝叶斯估计理论为非线性滤波提供了严谨的解决框架。对于线性高斯系统，贝叶斯估计的最优解为卡尔曼滤波[1]。但对于非线性高斯系统，很难得到高斯加权积分的解析解，因此科研人员提出了许多次优非线性滤波方法。其中，扩展卡尔曼滤波(Extented Kalman Filter,EKF)[2]由于简单高效得到广泛应用,但EKF采用非线性函数的一阶泰勒展开近似非线性函数，对于强非线性系统会产生较大的近似误差，且其需要计算雅可比矩阵，这既增加了计算复杂度也要求非线性函数连续可微。

为了克服EKF的缺点，随机采样型滤波器和确定采样型滤波器分别被提出，其核心是用一组随机或确定加权采样点逼近状态的后验分布，以采样点的加权和近似“非线性函数×高斯函数”的积分。随机采样型滤波器的主要应用形式——粒子滤波(Particle Filter,PF)[3]，以蒙特卡罗随机采样得到的粒子近似状态后验分布，理论上适用于解决任意非线性滤波问题，但存在权值退化、粒子多样性匮乏、实时性差等严重缺陷。依据采样点选取策略的不同，确定采样型滤波器主要分为中心差分卡尔曼滤波(Central Difference Kalman Filter,CDKF)[4]、无迹卡尔曼滤波(Unscented Kal-man Filter,UKF)[5]和容积卡尔曼滤波(Cubature Kalman Filter,CKF)[6]等。CDKF以多项式插值拟合逼近状态后验分布，计算简单但滤波精度较低且易受参数取值影响。UKF以UT(Unsented Transformation)变换逼近状态后验分布，能够以二阶泰勒精度逼近非线性状态而计算量与EKF同阶，但系统状态维数大于3时，中心采样点权值为负，从而引起协方差矩阵的非正定和滤波发散。CKF以三阶球面-径向容积准则逼近状态后验分布，其采样点权值始终为正，且有严格的数学证明，与UKF相比滤波精度更高而计算量相近，因此，近年来得到了广泛的应用。

为进一步提高CKF的精度，容积积分卡尔曼滤波(Cubature Quadrature Kalman Filter,CQKF)[7]以容积准则和高斯-拉盖尔积分准则近似高斯加权积分，滤波精度与切比雪夫-拉盖尔多项式的阶数m成正相关关系。CQKF是CKF的拓展形式，当m≥2时，其精度高于CKF。但CQKF要求系统模型和噪声精确已知，而现代战场复杂对抗环境使得系统模型具有很大的不确定性，系统状态突变，过程噪声及量测噪声未知时变，从而造成CQKF滤波精度下降甚至发散。为解决噪声统计特性未知情况下的滤波问题，贝叶斯法[8]、相关法[9-11]、协方差匹配法[12]和极大似然估计法[13]等多种噪声估计算法分别被提出。贝叶斯法涉及到多重积分，计算量大且未必能得到最优封闭解，多限于理论研究。相关法主要应用于线性系统，其在非线性系统中的拓展尚未无偏性证明[14]。协方差匹配法是一种有偏估计方法，存在稳态估计误差且估计精度相对较低。极大似然估计法由于能够直接构造含有待估计参数的概率密度函数，且计算量适中而得到广泛关注，其中以基于极大后验估计(Maximum A Posterior, MAP)准则提出的Sage-Husa时变噪声统计估值器[15]应用最为广泛。

基于上述考虑，本文提出了一种自适应强跟踪CQKF(AST-CQKF) 算法。AST-CQKF借鉴强跟踪滤波(Strong Tracking Filter, STF)的思想，引入时变渐消因子对预测协方差矩阵在线调整，同时利用Sage-Husa时变噪声统计估值器对噪声统计特性实时估计，并将估计结果引入滤波迭代过程中，从而增加了CQKF算法的鲁棒性和自适应性。通过仿真实验验证了本文算法的有效性和可行性。

1 容积积分卡尔曼滤波

1.1 贝叶斯滤波框架

考虑如下非线性系统：

(1)

式中：xk∈Rn为k时刻的状态向量；zk∈Rp为k时刻的量测向量；f:Rn→Rn和h:Rn→Rp为已知非线性函数；vk-1∈Rn和ηk∈Rp为不相关的高斯白噪声，且vk-1～N(0,Qk-1)，ηk～N(0,Rk);Qk-1和Rk为噪声协方差矩阵。

假设k-1时刻的后验概率密度函数为高斯分布，即

(2)

(3)

其中状态一步预测及协方差为

(4)

(5)

输出预测、自协方差及互协方差分别为

(6)

(7)

(8)

非线性系统式(1)在最小方差估计准则下的最优高斯滤波器为[16]

(9)

式中：

(10)

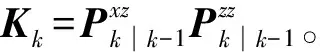
因此，贝叶斯滤波的核心问题转化为计算形式如式(11)的积分表达式：

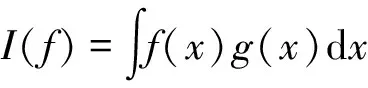
(11)

式中：f(x)为任意非线性函数;g(x)为高斯密度函数。通常式(11)难以得到解析表达式，主要采取一系列采样点ξj及其权值wj的加权和进行数值近似，即

(12)

1.2 容积积分准则

对于任意函数f(x)，X∈Rn，式(11)的一般形式为

(13)

可以在球面坐标系中表示为[7]

μ)ds(Z)]rn-1e-r2/2dr

(14)

式中：X=CrZ+μ，且X～N(μ,Σ)，μ为高斯分布的均值，C为协方差矩阵Σ的Cholesky分解，即Σ=CCT；r和Z为积分变量；Un={Z∈RnZZT=1}为单位超球面；ds(·)为Un上的面积元素。

若μ=0且Σ为单位矩阵，则式(14)中的积分为

(15)

由三阶球面-径向容积准则可以近似为

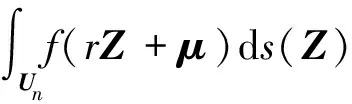
(16)

式中：Γ(·)为伽马函数；[ui](i=1,2,…,2n)为位于单位超球面与坐标轴交点的容积点，即完全对称点集[1]的第i个列向量

[1]=

(17)

将式(16)代入式(14)，令λ=r2/2，则

λ(n/2-1)e-λdλ

(18)

根据高斯-拉盖尔积分准则，积分可以近似为

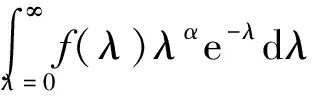
(19)

式中：积分点λj(j=1,2,…,m)为m阶切比雪夫-拉盖尔多项式的m个根，即λj满足

(m+α)(m+α-1)λm-2-…=0

(20)

式中：α=n/2-1。

对应的权值Aj为

(21)

将式(19)～式(21)代入式(18)，则得到容积积分准则为

(22)

由式(22)可知，对于如式(1)所示的n维状态估计问题，需要计算满足

(23)

的2mn个采样点ξl(本文称其为CQ点)及对应权值wl，其计算方式如下：

i=1,2,…,2n；j=1,2,…,m；l=1,2,…,2mn

(24)

(25)

1.3 CQKF算法

步骤1初始化。

1) 令

2) 根据式(24)和式(25)计算CQ点ξl及对应权值wl。

步骤2预测更新。

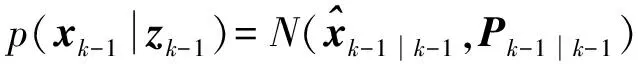
2) 计算CQ点：

3) 更新CQ点随状态方程的转移：

4) 计算一步状态预测及预测误差协方差矩阵：

步骤3量测更新。

1) 分解协方差矩阵:

2) 计算CQ点:

3) 更新CQ点随量测方程的转移:

Zl,kk-1=h(χl,kk-1)

4) 计算量测预测值：

5) 计算自协方差矩阵及互协方差矩阵：

6) 计算卡尔曼增益：

7) 估计状态：

8) 估计状态预测误差协方差矩阵：

2 强跟踪滤波理论

为了提高EKF对于系统模型不确定性及状态突变的鲁棒性，周东华等[17]提出的STF利用衰减记忆滤波思想，在计算预测误差协方差矩阵时引入渐消因子，强迫残差序列正交，从而保证滤波器对系统实际状态的跟踪效果。

非线性系统式(1)的STF方程为[18]

(26)

式中：

In×n为n阶单位矩阵；λk为渐消因子，其计算式为

(27)

式中：

(28)

(29)

(30)

(31)

其中：tr(·)为矩阵求迹运算；β≥1为弱化因子；0<ρ≤1为遗忘因子,通常取ρ=0.95。由于STF是EKF的改进形式，在计算渐消因子时仍需要求解雅可比矩阵，因此不能直接将其引入CQKF，需要研究不利用Hk计算渐消因子的等价表述方式。文献[19]给出了Hk、Nk和Mk的等效表述形式，即

(32)

(33)

(34)

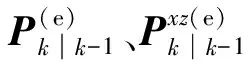
(35)

渐消因子的具体引入方式见第4节。

3 时变噪声统计估值器

考虑噪声的一般形式，即vk-1∈Rn和ηk∈Rp是带时变均值和协方差且线性无关的高斯白噪声，且vk-1～N(qk-1,Qk-1)，ηk～N(rk,Rk)。针对qk、Qk、rk和Rk等噪声参数的估计问题，文献[15]基于MAP准则得到了Sage-Husa噪声统计估值器，并给出了最优MAP估值器、次优MAP估值器、次优无偏MAP估值器和时变噪声统计估值器等多种形式。文献[20]和文献[21]分别将其拓展到UKF和CKF，给出了适用于UKF和CKF的递推算法。由于UKF、CKF和CQKF同属确定采样型滤波器，借鉴UKF和CKF的递推形式，得到如下适用于CQKF的次优无偏MAP常值噪声统计估计器：

(36)

(37)

(38)

(39)

对于时变噪声统计而言，应当强调新近数据的作用，逐渐遗忘陈旧数据。选取加权系数{γi}，使之满足

(40)

于是有

(41)

式中：b为遗忘因子。将次优无偏MAP常值噪声统计估计器中的加权和系数1/k替换为{γi}，即得到适用于CQKF的时变噪声统计估值器：

(42)

(43)

(44)

(45)

4 自适应强跟踪CQKF

将时变渐消因子和时变噪声统计估值器嵌入标准CQKF，并将其拓展到噪声均值非零的情形，即可得到AST-CQKF算法，流程如图1所示。

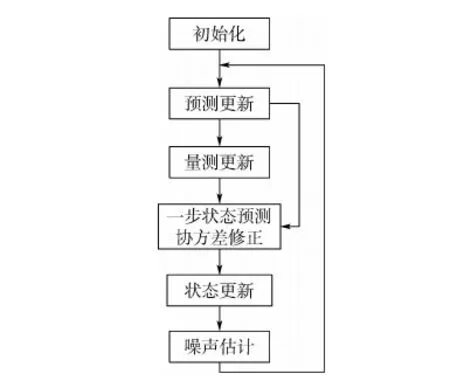
图1 AST-CQKF算法流程图Fig.1 AST-CQKF algorithm flowchart

算法具体流程如下：

步骤1初始化。

1) 令

2) 根据式(24)和式(25)计算CQ点ξl及对应权值wl。

步骤2预测更新。

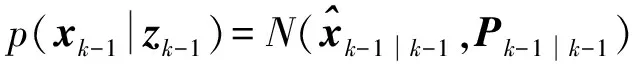
2) 计算CQ点:

3) 计算CQ点随状态方程的转移:

4) 计算一步状态预测及预测误差协方差矩阵：

步骤3量测更新。

1) 分解协方差矩阵:

2) 计算CQ点:

3) 计算CQ点随量测方程的转移:

4) 计算量测预测值:

5) 计算自协方差矩阵和互协方差矩阵：

步骤4一步状态预测协方差修正。

1) 根据式(35)计算渐消因子λk。

2) 利用λk修正一步状态预测协方差矩阵：

3) 分解修正后的协方差矩阵：

4) 计算CQ点：

5) 计算CQ点经量测方程的转移:

6) 计算量测预测值:

7) 计算自协方差矩阵和互协方差矩阵:

步骤5状态更新。

1) 计算卡尔曼增益：

2) 估计状态:

3) 估计状态预测误差协方差矩阵：

步骤6噪声估计。

根据式(42)～式(45)对噪声统计特性递推估计。

5 仿真验证

考虑一个典型的二维平面雷达跟踪问题[7]，目标以固定未知转弯速率Ω做圆周运动,其状态方程为

Xk-1+vk-1

(46)

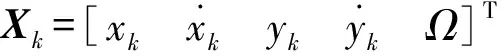
(47)

雷达固定于坐标原点，对目标的距离rk及方位角θk进行测量，则量测方程为

(48)

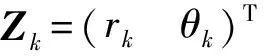
初始状态真实值为

对应的协方差矩阵为

P00= diag[100 m210 m2/s2100 m210 m2/s2

100 m·rad2/s2]T

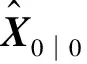
(49)

(50)

(51)

为验证算法在系统状态模型不准确及噪声统计特性不准确下的有效性，设置以下2种仿真情形。

5.1 系统量测噪声的统计特性不准确

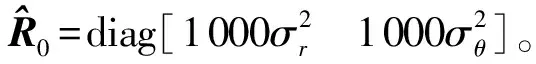
由图2可知，通过AST-CQKF算法得到的位置、速度均方根误差明显小于CQKF算法，而转弯率均方根误差基本相同，可见AST-CQKF算法能够有效减小噪声统计特性不准确带来的估计误差，提高估计精度。此外，噪声统计特性的改变对位置、速度、转弯率的影响程度不同，对位置影响最大，速度次之，转弯率几乎无影响。

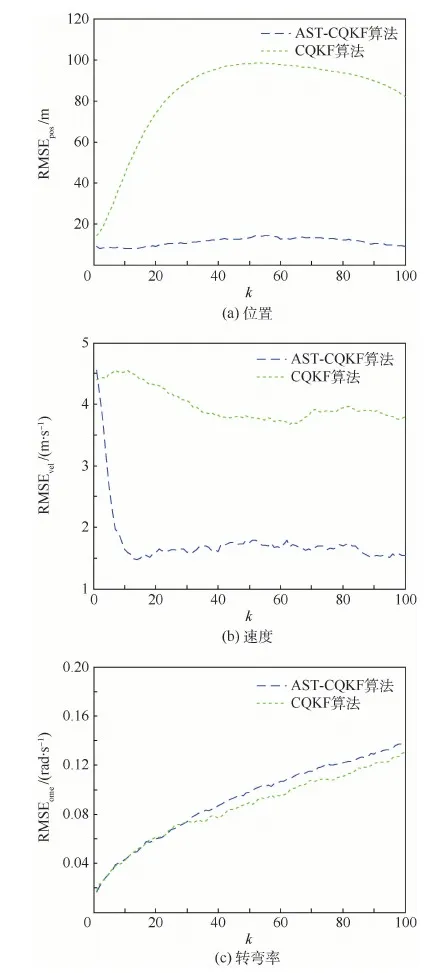
图2 跟踪均方根误差(情形1)Fig.2 RMSE tracking(Case 1)

5.2 系统状态模型不准确

为设置系统模型的不确定性，将式(46)变形得

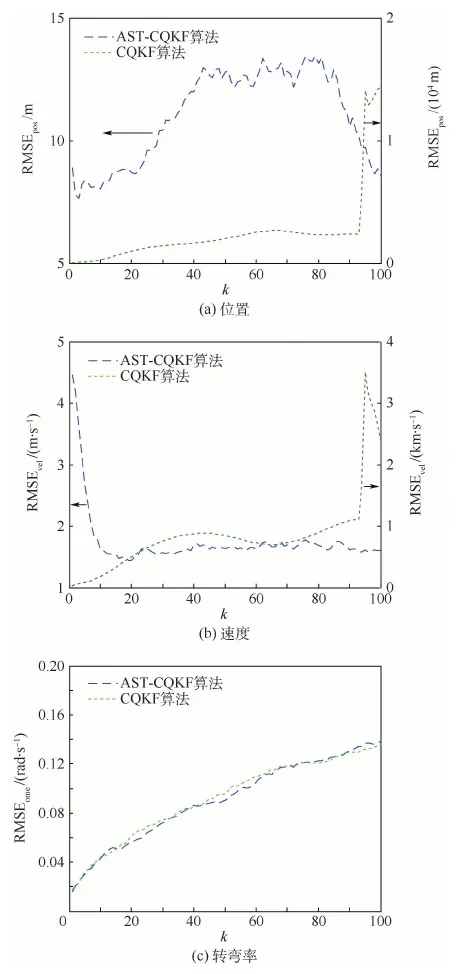
图3 跟踪均方根误差(情形2)Fig.3 RMSE tracking(Case 2)

Xk=

Xk-1+vk-1

(52)

式中：a和c为可调节的参数，模型正常时两者均为1，通过设置不同的系数以模拟系统状态模型的不确定性，本文设定a=1.1，c=1.2。仿真过程中，状态真值由精确的状态方程得到，而滤波器使用不精确的状态方程进行状态估计，以此比较AST-CQKF与CQKF算法在系统状态模型不准确时的滤波精度。经过200次独立的蒙特卡罗仿真，得到位置、速度、转弯率的RMSE结果分别如图3所示(情形2)。

由图3可知，系统状态模型不准确时，CQKF在仿真开始后迅速发散，无法对目标保持跟踪，而AST-CQKF算法虽然不能完全消除模型不确定性的影响，但能够防止滤波发散，保持滤波收敛性，对于模型不确定型具有鲁棒性。

设置不同的仿真步数与仿真次数，得到CQKF算法与AST-CQKF算法的仿真计算时间如表1所示。由表1可以看出，与前者相比，后者的仿真计算时间增加了一倍左右，尤其是仿真次数较多时，计算时间的增加更为明显，这是由于AST-CQKF算法步骤更多、复杂度更高引起的。但单次仿真时，2种算法的时间均小于0.1 s，因此与滤波精度的提高相比，AST-CQKF算法的时间增加处于可接受的范围内。

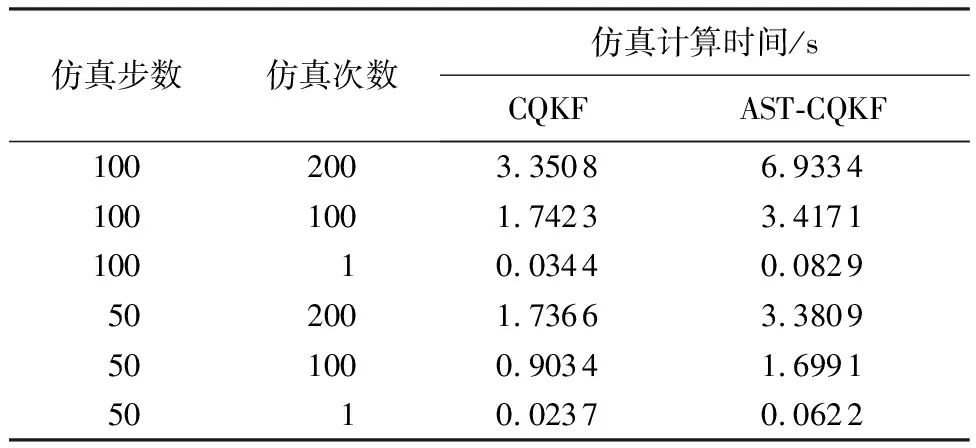
表1 CQKF与AST-CQKF算法蒙特卡罗仿真计算时间Table 1 Calculation time of Monte Carlo simulation in CQKF and AST-CQKF algorithm

6 结 论

CQKF算法在复杂对抗环境下的目标跟踪主要存在2方面问题：①系统状态空间模型发生突变导致滤波发散；②噪声统计特性发生改变或不精确造成滤波精度下降。针对该问题，本文提出了一种新的自适应强跟踪CQKF(AST-CQKF)算法应用到目标跟踪：

1) 将强跟踪滤波器与CQKF相结合，给出了适用于CQKF的渐消因子计算方法，利用渐消因子修正一步状态预测协方差矩阵，进而用于状态估计，克服了模型不准确影响滤波精度和滤波稳定性的问题，改善了CQKF的跟踪性能。

2) 利用Sage-Husa时变噪声统计估值器对噪声实时估计，得到了AST-CQKF算法，增强了滤波器对于噪声统计特性变化的自适应能力，有效地提高了滤波精度。

3) 仿真结果表明，在系统量测噪声统计特性不准确或状态空间模型不准确的情况下，CQKF算法的滤波精度急剧下降甚至滤波发散， AST-CQKF算法则能够实现系统状态的快速准确跟踪，有效地克服了CQKF算法的局限性。

参考文献 (References)

[1] KALMAN R E.A new approach to linear filtering and prediction theory[J].Transactions on ASME Journal of Basic Engineering,1960,82(D):35-46.

[2] JAZWINSKI A H.Stochastic processes and filtering theory[M].New York:Academic Press,1970:235-237.

[3] 李天成,范红旗.孙树栋.粒子滤波理论、方法及其在多目标跟踪中的应用[J].自动化学报,2015,41(12):1981-2002.

LI T C,FAN H Q,SUN S D.Particle filtering:Theory,approach,and application for multitar-get tracking[J].Acta Automatica Sinica,2015,41(12):1981-2002(in Chinese).

[4] 韩萍,干浩亮,何炜琨,等.基于迭代中心差分卡尔曼滤波的飞机姿态估计[J].仪器仪表学报,2015,36(1):187-193.

HAN P,GAN H L,HE W K,et al.Iterated central difference Kalman filter based aircraft attitude estimation[J].Chinese Journal of Scientific Instrument,2015,36(1):187-193(in Chinese).

[5] 王宝宝，吴盘龙. 基于平方根无迹卡尔曼滤波平滑算法的水下纯方位目标跟踪[J].中国惯性技术学报,2016,24(2):180-184.

WANG B B,WU P L.Underwater bearing-only tracking based on square-root unscented Kalman filter smoothing algorithm[J].Journal of Chinese Inertial Technology,2016,24(2):180-184(in Chinese).

[6] 张龙,崔乃刚,杨峰,等.高阶容积卡尔曼滤波及其在目标跟踪中的应用[J].哈尔滨工程大学学报,2016,37(4):573-578.

ZHANG L,CUI N G,YANG F,et al.High-degree cubature Kalman filter and its application in target tracking[J].Journal of Harbin Engineering University,2016,37(4):573-578(in Chinese).

[7] BHAUMIK S,WATI S.Cubature quarature Kalman filter[J]. IET Signal Processing,2013,7(7):533-541.

[8] LAINIOTIS D G.Optimal adaptive estimation:Structure and parameters adaption[J].IEEE Transactions on Automatic Control,1971,16(2):160-170.

[9] MEHRA R K. On the identification of variances and adaptive filtering[J].IEEE Transactions on Automatic Control,1970,15(2):175-184.

[10] ODELSON B J,RAJAMANI M R,RAWLINGS J B.A new autocovariance least-squares method for estimating noise covariances[J].Automatica, 2006,42(2):303-308.

[11] AKESSON B M,JORGENSON J B,POULSEN N K,et al.A generalized autocovariance least-squares method for Kalman filter tuning[J].Journal of Process Control,2008,18(7-8):769-779.

[12] MYERS K A,TAPLEY B D.Adaptive sequential estimation with unknown noise statistics[J].IEEE Transactions on Automatic Control,1976,21(8):520-523.

[13] KASHYAP R L.Maximum likelihood identification of stochastic linear systems[J].IEEE Transactions on Automatic Control,1970,15(1):25-34.

[14] LIMA F V, RAJAMANI M R, SODERSTROM T A,et al.Covariance and state estimation of weakly observable systems:Application to polymerization processes[J].IEEE Transactions on Control Systems Technology,2013,21(4):1249-1257.

[15] 李宁,祝瑞辉,张勇刚.基于Sage-Husa算法的自适应平方根CKF目标跟踪方法[J].系统工程与电子技术,2014,36(10):1899-1905.

LI N,ZHU R H,ZHANG Y G.Adaptive square CKF method for target tracking based on Sage-Husa algorithm[J].Systems Engineering and Electronics,2014,36(10):1899-1905(in Chinese).

[16] 王小旭,潘泉,黄鹤,等.非线性系统确定采样型滤波算法综述[J].控制与决策,2012,27(6):801-812.

WANG X X,PAN Q,HUANG H,et al.Overview of deterministic sampling filtering algorithms for nonlinear system[J].Control and Decision,2012,27(6):801-812(in Chinese).

[17] 周东华，席裕庚，张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6):689-695.

ZHANG D H,XI Y G,ZHANG Z J.A suboptimal multiple fading extended Kalman filter[J].Acta Automatica Sinica, 1991,17(6):689-695(in Chinese).

[18] 方君,戴邵武,许文明,等.基于ST-SRCKF的超高速强机动目标跟踪算法[J].北京航空航天大学学报,2016,42(8):1698-1708.

FANG J,DAI S W,XU W M,et al.Highly maneuvering hypervelocity-target tracking algorithm based on ST-SRCKF[J].Journal of Beijing University of Aeronautics and Astronautics,2016,42(8):1698-1708(in Chinese).

[19] 张龙,崔乃刚,王小刚,等.强跟踪-容积卡尔曼滤波在弹道式再入目标跟踪中的应用[J].中国惯性技术学报,2015,23(2):211-218.

ZHANG L,CUI N G,WANG X G,et al.Strong tracking-cubature Kalman filter for tracking ballistic reentry target[J].Journal of Chinese Inertial Technology,2015,23(2):211-218(in Chinese).

[20] 赵琳,王小旭,孙明,等.基于极大后验估计和指数加权的自适应UKF滤波算法[J].自动化学报,2010,36(7):1007-1019.

ZHAO L,WANG X X,SUN M,et al.Adaptive UKF filteing algorithm based on maximum a posterior estimation and exponential weighting[J].Acta Automatica Sinica,2010,36(7):1007-1019(in Chinese).

[21] 丁家琳,肖建,赵涛.自适应CKF强跟踪滤波器及其应用[J].电机与控制学报,2015,19(11):111-120.

DING J L,XIAO J,ZHAO T.Adaptive CKF strong tracking filter and application[J].Electric Machines and Control,2015,19(11):111-120(in Chinese).