采用FRM的窄过渡带奇型排列结构改进方法
张文旭, 赵文童, 陈涛, 陈亚静
(哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)
在数字信道化系统设计中,数字信道化的过程实质上就是利用滤波器组进行均匀或非均匀设计的过程。滤波器组技术作为信号处理的一种常见方法和手段,其应用范围很广,如通信、图像处理、语音、雷达等[1-3]。其中,具有窄过渡带特点的滤波器组计算复杂度高的问题业已成为该研究方向亟待解决的问题之一[4]。频率响应屏蔽(FRM)技术因其在解决窄过渡带滤波器组设计中具有明显优势而得以推广[5]。
文献[6]运用凸规划算法设计FRM结构中的滤波器,并提出了3种优化算法;文献[7]针对工程应用方面在经典FRM滤波器结构的基础上优化设计二级FRM滤波器,这种优化方法虽然可以消除内插因子的约束条件,但是屏蔽滤波器的设计较为复杂;文献[8-9]利用FRM技术设计任意带宽的FIR数字滤波器,降低了计算的复杂度,但是因为滤波器都在这2种结构的前置位,所以这2种结构都会受到采样率的限制;文献[10]提出了一种基于FRM的DFT滤波器组优化算法,相比于传统的DFT滤波器组在一定程度上降低了计算复杂度。重构滤波器组也是滤波器组研究的重要组成部分,文献[11]通过窗函数设计FRM滤波器,虽然设计的综合滤波器组计算复杂度很高,但是为重构滤波器设计提供了一种新的思路;文献[12]将屏蔽技术应用到非均匀滤波器组的结构构造中,根据多速率理论提出了一种低复杂度的综合滤波器设计方法;文献[13]运用FRM结构设计两通道窄过渡带的完全重构滤波器组,缺点是在实现时计算量比较大。文献[13]提出了一种基于FRM的偶型排列信道化改进结构,缺点是偶型排列结构的第0个信道输出IQ量不正交,需要对输出信号单独进行希尔伯特变换,这样第0个信道的延时会与其他信道不同。
本文将FRM技术在窄过渡带滤波器组设计中的优势推广到分析滤波器组高效结构设计中,由于奇型排列结构所有信道输出特性完全一致,不像偶型排列结构中第0个信道输出IQ量不正交,故而本文主要以奇型排列结构为研究重点。本文提出了一种采用FRM的窄过渡带奇型排列非最大抽取改进结构,该改进结构针对非最大抽取系统进行设计,不受信道数和抽取数的限制,适用性更加广泛。
1 频率响应屏蔽技术
FRM技术适用于窄过渡带滤波器设计,因为其在降低滤波器阶数和减少计算复杂度方面有很好的效果。FRM滤波器的基本框架如图1所示,其传递函数的z变换可表示为[14-15]
H(z)=Ha(zL)HMa(z)+
(z-L(Na-1)/2-Ha(zL))HMc(z)
(1)
式中:Ha(z)为原型滤波器;HMa(z)和HMc(z)为屏蔽滤波器;Na为原型滤波器Ha(z)的长度;L为插值倍数。
滤波器插值过程如图2所示,上图为滤波器插值之前的幅频特性,下图为滤波器插值之后的幅频特性。屏蔽滤波器的作用是对插值所产生的滤波器多余镜像进行屏蔽。
(2)
(3)

图1 FRM滤波器的基本框架Fig.1 Basic framework of FRM filter
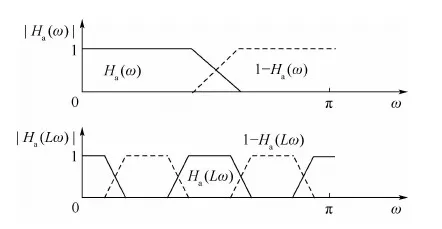
图2 滤波器插值过程(L=4)Fig.2 Process of filter interpolation for L=4

(4)
式中:ha(n)、hMa(n)和hMc(n)的系数具有偶对称性;N1和N2分别为屏蔽滤波器HMa(z)和HMc(z)的长度;M1和M1的取值情况如下:
(5)
将信号延时L(Na-1)/2个点后与Ha(zL)相减可以得到下支路的输出。考虑到插值L的数值不被限制,滤波器Ha(z)长度Na应为奇数。在对2个屏蔽滤波器的输出进行合成时,要求滤波器HMa(z)和HMc(z)长度同为奇数或者同为偶数。
令零相位H(z)的频率响应为
H(ω)=H1(ω)+H2(ω)
(6)
又因为z-L(Na-1)/2-Ha(zL)可看作Ha(z)进行L倍插值后的互补滤波器,则
H1(ω)=Ha(Lω)HMa(ω)
(7)
H2(ω)=(1-Ha(Lω))HMc(ω)
(8)
式中:Ha(ω)、HMa(ω)和HMc(ω)分别为Ha(z)、HMa(z)和HMc(z)的零相位频率响应。
FRM滤波器频带合成过程图[12,16]如图3所示,从上至下第1幅图中实线为原型滤波器Ha(ω)插值后的幅频特性,虚线为屏蔽滤波器HMa(ω)的幅频特性;第2幅图中实线为原型滤波器Ha(ω)的互补滤波器插值后的幅频特性,虚线为屏蔽滤波器HMc(ω)的幅频特性;第3幅图中实线为对插值后的原型滤波器进行屏蔽得到的H1(ω)幅频特性,虚线为对插值后的原型滤波器的互补滤波器进行屏蔽得到的H2(ω)幅频特性;第4幅图为最终得到的FRM滤波器的幅频特性。

图3 采用FRM技术设计低通滤波器[12,16]Fig.3 Design of low-pass filter based on FRM[12,16]
2 调制滤波器组
2.1 滤波器组频带划分
调制滤波器组在调制类型划分方面分为2种类型,分别为余弦调制和复指数调制。余弦调制可以看作复指数调制的特例。调制滤波器组在频带划分结构设计上也分为2种类型,分别为奇型排列和偶型排列。针对实际问题,笔者研究了调制滤波器组的奇型排列方式,并且对滤波器组中的M个滤波器进行均匀调制,滤波器组频带划分方式如图4所示。
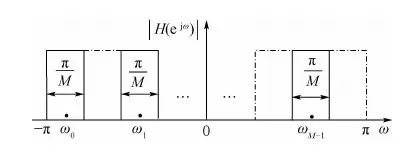
图4 滤波器组频带划分Fig.4 Band division of filter bank
图4所示的奇型排列的划分方式避免了因为实信号造成的信道冗余问题,而且能够实现信号的无盲区无混叠接收。上述排列方式的虚线频带为对应的镜像,第k个信道对应的中心频率ωk满足:
(9)
2.2 高效信道化结构
均匀滤波器组低通实现结构如图5所示。假设信道数为M,抽取倍数为K,令M=FK,令F取正整数(当F=1时为临界抽取情况),输入信号为s(n),复指数调制因子为ejωkn,低通滤波器为g(n),原型滤波器阶数为N,多相滤波器阶数为T=N/M。输入信号经过信道化后的输出信号表示为yk(m),k=0,1,…,M-1,m=0,1,…。
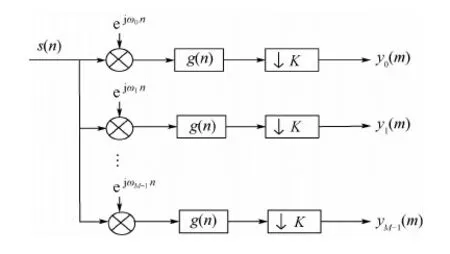
图5 滤波器组低通实现结构Fig.5 Low-pass structure of filter bank
如图5所示,第k个信道的输出信号可以表示为
yk(m)=(s(n)ejωkn)⊗g(n)n=mK=
(10)
式中:⊗表示卷积运算;k=0,1,…,M-1。
令信号K倍抽取后的多相结构表达式为sp(m)=s(mK-p),滤波器多相分量表达式为gp(m)=g(mM+p),令i=iM+p,p=0,1,…,M-1,则式(10)可以表示为
(11)
令l=iF,hp(i)=gp(i/F),则hp(i)是gp(i)的F倍内插,第k个信道的输出信号表示为
(12)
则式(12)的z变换可以表示为
(13)
滤波器组中的M个滤波器通带带宽减少为之前的1/M,所以在对滤波器K(K≤M)倍抽取时不会产生混叠现象。将中心频率ωk代入式(13)中,K倍抽取提前,可得对应的奇型排列信道化高效结构,如图6所示。该高效结构将抽取模块提到信道化结构最前端,使之适应于高速系统中。

图6 滤波器组信道化高效结构Fig.6 Efficient channelization structure of filter bank
3 窄过渡带奇型排列高效结构
3.1 FRM高效结构
设FRM原型滤波器z变换表达式P(z)为
P(z)=Hap(zL)HMap(z)+Hcp(zL)HMcp(z)
(14)
式中:Hap(z)、HMap(z)和HMcp(z)分别为长度为Nao、NMa和NMc的零相位对称滤波器;Hcp(z)=1-Hap(z)。
可以得到滤波器的因果线性相位形式为
Hao(z)=z-L(Nao-1)/2Hap(zL)
(15)
Hco(z)=z-L(Nco-1)/2Hcp(zL)
(16)
HMa(z)=z-(NMac-1)/2HMap(z)
(17)
HMc(z)=z-(NMac-1)/2HMcp(z)
(18)
式中:NMac=max{NMa,NMc}。
将式(15)~式(18)代入式(14),则可以得到FRM滤波器组的各通道传递函数表达式为
(19)
式中:k=0,1,…,M-1;a=(Np-1)/2,Np=L(Nao-1)+NMac;WM=e-j2π/M。
将滤波器的因果线性相位形式进行多相分解,可得如下表达式:
(20)
(21)
(22)
(23)
式中:l=0,1,…,M-1;p=0,1,…,M-1。
将式(20)~ 式(23)代入式(19),即可得到FRM滤波器组各通道传递函数的多相结构表达式为
(24)
在对L倍插值之后的滤波器进行屏蔽时,需要M通道屏蔽滤波器组的正好可以覆盖插值产生的多余镜像,即L=IM,I=1,2,…。原型滤波器和屏蔽滤波器需要满足:
ωmap=ωap/L+π(L/M′-1)/L
(25)
ωmas=π/L+ωap/L+π(L/M′-1)/L
(26)
ωmcp=ωas/L+π(L/M′-1)/L
(27)
ωmcs=π/L+ωas/L+π(L/M′-1)/L
(28)
式中:M′为信道数;ωap和ωas分别为Hap的通带和阻带截止频率;ωmap、ωmas、ωmcp、ωmcs分别为屏蔽滤波器HMap(z)和HMcp(z)的通带截止频率和阻带截止频率。
又由于实信号的频谱应为正值,且关于kπ(k=0,1,…)对称,只需考虑0~π的信道信号,则数值上M′=2M,M表示实际应用信道数数目。
假设上半个支路的屏蔽滤波器为原型屏蔽滤波器,那么对原型屏蔽滤波器进行π/L频移就能够得到下半支路的屏蔽滤波器,然后再把上下2个支路进行合并就能够得到带宽为π/M的子带。FRM滤波器频率响应的合成过程如图7所示,从上至下第1幅图中实线为原型滤波器Ha(ω)的幅频特性,虚线为原型滤波器Ha(ω)的互补滤波器的幅频特性;第2幅图中实线为插值后的原型滤波器Ha(ω)的幅频特性,虚线为插值后的原型滤波器Ha(ω)的互补滤波器的幅频特性;第3幅图为屏蔽滤波器HMa(ω)的幅频特性;第4幅图为屏蔽滤波器HMc(ω)的幅频特性;第5幅图为最终合成的FRM滤波器H(ω)的幅频特性。
将FRM技术引入信道化高效结构中的滤波器设计中。用式(24)中FRM滤波器组的M个滤波器代替式(13)中滤波器组中的M个滤波器,可以得到第k个信道输出信号的表达式为
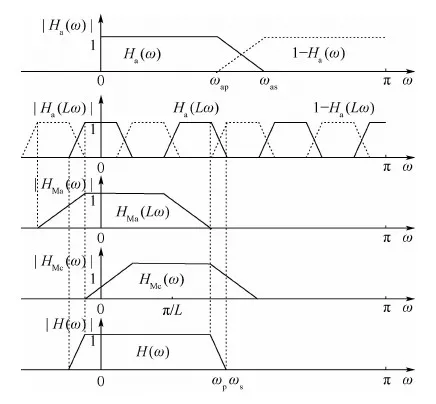
图7 FRM滤波器的频率响应合成过程Fig.7 Frequency response synthesis process of FRM filter

(29)
又因为Hco(z)=z-L(Nao-1)/2-Hao(z),满足:
(30)
式中:q为L(Nao-1)/(2M)的余数,q=0,1,…,M-1。
由式(29)、式(30)结合图6,将K倍抽取提前,可得基于FRM的窄过渡带滤波器组高效结构,如图8所示。

图8 采用FRM的窄过渡带奇型排列高效结构Fig.8 Odd-arrangement efficient structure with narrow transition band based on FRM
3.2 奇型排列高效结构复杂度分析
高效结构的计算复杂度主要受到硬件实现所需的乘法器数量影响,因此复杂度数值用于表征高效结构中的乘法器数量。滤波器中所用的乘法器数目与滤波器长度成反比,即复杂度数值与过渡带宽成反比。令实现滤波器组的代价函数为C。
实现一个均匀滤波器组所需要的乘法器数目为
Cr=Mγ/Δf
(31)
式中:γ为比例系数;M为信道数;Δf为窄过渡带滤波器的归一化过渡带宽。
同理,实现一个滤波器组的多相结构的复杂度为
Cp=γ/Δf+MlbM+2M
(32)
本文设计方法实现的代价函数为
CFRM=γ/ΔHa+2γ/ΔHm+2MlbM+2M
(33)
式中:ΔHa为原型滤波器的归一化过渡带宽;ΔHm为屏蔽滤波器的归一化过渡带宽。
在FRM滤波器中,假设ωp为通带截止频率,ωs为阻带起始频率,其归一化过渡带宽为Δf=ωs-ωp;θ为原型滤波器的通带截止频率,φ为原型滤波器的阻带截止频率;插值倍数为L,则原型滤波器的过渡带宽可以表示为ΔHa=LΔf。通带和阻带纹波对滤波器设计复杂度影响并不敏感,故而暂不考虑纹波的影响。
原型滤波器采用半带滤波器。由图7可知,屏蔽滤波器的过渡带宽为ΔHm=1/L。将所有滤波器的过渡带宽表达式代入式(33)可得到
CFRM=γ/(LΔf)+2γL+2MlbM+2M
(34)
内插因子L数值的选择会影响整个原型滤波器和屏蔽滤波器的设计复杂度。根据复杂度最低准则,可以得到最优L值的表达式为
(35)
因为L为正整数,取
(36)
式中:round(X)表示取距离X最近的整数。当要求L为M的整数倍时,L取值为M′的最小倍数。L值代入式(33)可得
(37)
根据式(31)~式(33)可知,本文FRM改进方法可以降低滤波器组的计算复杂度。在设计原型低通滤波器时采用半带滤波器,因为半带滤波器有近一半的值为零,因此可以进一步有效减少计算量。在设计2个屏蔽滤波器时,可以先设计其中一个屏蔽滤波器,再通过调制这个屏蔽滤波器得到另一个屏蔽滤波器。通过这种设计方法得到的2个屏蔽滤波器的通带宽度和阻带宽度都是相等的,所以可以使设计复杂度再次降低。
4 系统仿真及分析
4.1 FRM滤波器组仿真与复杂度分析
设置滤波器组通道数M=8,内插因子L=16,窄过渡带归一化过渡带宽为0.004。设计原型滤波器时采用半带滤波器,利用MATLAB中的firpm函数进行设计,通带和阻带截止频率分别为0.468和0.532,长度Nao=79,滤波器的幅频响应如图9所示。由式(25)、式(26)可得原型屏蔽滤波器的通带截止频率为0.029,阻带截止频率为0.092,长度NMac=82,幅频响应如图10所示。合成之后的FRM滤波器幅频响应如图11所示。所设计的FRM滤波器组幅频响应如图12所示。
在设计得到的滤波器过渡带相同的情况下,直接实现这样的滤波器组结构需要乘法器数量为1 280×8=10 240,滤波器组的多相实现结构需要乘法器数量为1 280+8lb 8+16=1 307。在采用了79阶数半带滤波器的设计中,实际非零系数为40,则本文提出的窄过渡带滤波器组改进结构所需的乘法器数为40+86×2+2×8lb 8+16=251。而文献[9]需要乘法器数目为125+150+146+2×8lb 8+16=460。通过对比本文提出的窄过渡带滤波器组改进结构,可以发现该改进结构比直接实现结构节省了97.5%的乘法器资源,比多相滤波器组高效结构节省了80.8%的乘法器资源,比文献[9]提出的高效结构节省了45.4%的乘法器资源。因此,本文中所提出的窄过渡带滤波器组改进结构实现了计算复杂度的降低,更加易于工程应用实现。
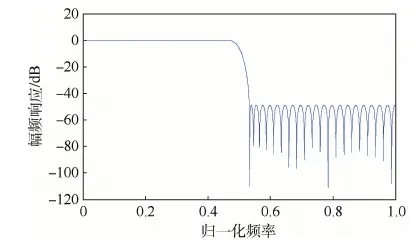
图9 原型滤波器幅频响应Fig.9 Amplitude-frequency response of prototype filter

图10 原型屏蔽滤波器幅频响应Fig.10 Amplitude-frequency response of prototype masking filter

图11 FRM滤波器幅频响应Fig.11 Amplitude-frequency response of FRM filter

图12 FRM滤波器组幅频响应Fig.12 Amplitude-frequency response of FRM filter bank
4.2 FRM高效结构性能仿真与分析
用MATLAB进行仿真时,设置采样频率为960 MHz,信道数为8。同时输入7个信号,信号各项参数设置如表1所示。
图13为FRM高效结构的仿真输出信号频谱, LFM1跨信道3、4输出; AM1在信道5输出; LFM2在信道2输出; DSB1在信道6输出; LFM3在信道1输出; DSB2在信道7输出; AM2在信道0输出。通过将得到的信号频谱图与仿真输入信号进行对比,可以验证出FRM高效结构的正确性。
LFM1的起始频率60 MHz处于3、4信道的中心处,截止频率为80 MHz,故LFM1出现了跨信道的现象。LFM3的起始频率为320 MHz,截止频率为358 MHz,其频谱位于信道1和7的中心附近,由于滤波器组过渡带窄的原因并未出现跨信道现象。采用了FRM窄过渡带设计结构没有产生信号跨信道的现象。所以采用FRM窄过渡带的信道化结构可以减少信号跨信道现象,但是想要完全消除这种现象还是无法做到的。

表1 输入信号参数设置

图13 FRM滤波器组输出频域波形Fig.13 Output frequency domain waveform of FRM filter bank
5 结 论
1) 本文提出的一种采用FRM的窄过渡带奇型排列改进结构以通用性较强的非最大抽取系统为设计出发点,具有广泛的适用性。
2) 结构中下采样模块位于该高效结构的前置位,解决了由于采样率的限制不能应用于高速信号处理系统的问题。
3) 该改进结构相比于多相滤波高效结构具有更低的计算复杂度,为工程化实现奠定了理论与技术基础。
参考文献 (References)
[1] HARRIS F J,DICK C,RICE M.Digital receivers and transmi-tters using polyphase filter banks for wireless communication[J].IEEE Transactions on Microwave Theory and Techniques,2003,51(4):1395-1412.
[2] BARROS A K,RUTKOWSKI T,LTAKURA F.Estimation of speech embedded in a reverberant and noisy environment by independent component analysis and wavelets[J].IEEE Transactions on Neural Networks,2002,13(4):888-893.
[3] DO M N,VETTERLI M.The contourlet transform: An efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing,2005,14(12):2091-2106.
[4] HONG Y,LIAN Y.Continuous-time FIR filters based on frequency-response masking technique[C]∥2015 IEEE International Conference on Digital Signal Processing. Piscataway,NJ:IEEE Press,2015:191-195.
[5] ROMERO D E T.High-speed multiplierless frequency response masking(FRM) FIR filters with reduced usage of hardware resources[C]∥2015 IEEE 58th International Midwest Symposium on Circuits and Systems. Piscataway,NJ:IEEE Press,2015:1-4.
[6] LU W,HINAMOTO T.A unified approach to the design of interpolated and frequency-response-masking FIR filters[J].IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers,2016,63(12):2257-2266.
[7] WEI Y,HUANG S G,MA X J.A novel approach to design low-cost two-stage frequency response masking filters[J].IEEE Transactions on Circuits and Systems,2015,62(10):982-986.
[8] SHEN T,LIM Y C.Low complexity frequency-response masking filters using modified structure based on serial masking[C]∥19th European Signal Processing Conference. Kessariani:EURASIP,2011:1400-1404.
[9] 陈涛,王莹,刘勇.基于频率响应屏蔽的窄过渡带信道化接收机[J].吉林大学学报,2015,45(1):335-340.
CHEN T,WANG Y,LIU Y.Digital channelized receiver with narrow transiton band based on FRM filter[J].Journal of Jilin University,2015,45(1):335-340(in Chinese).
[10] LI N,NOWROUZIAN B.Application of frequency-response masking technique to the design of a novel modified-DFT filter banks[C]∥IEEE ISCAS,2006:3293-3296.
[11] KUMAR A,SUNKARIA R K.Design of prototype filter using windowing and linear optimization technique for the non-uniform filter banks[C]∥2013 International Conference on Recent Trends in Information Technology. Piscataway,NJ:IEEE Press,2014:352-358.
[12] SUMEDH D,SMITHA K G,VINOD A P.A low complexity reconfigurable channel filter based on decimation,interpolation and frequency response masking[C]∥2013 IEEE International Conference on Acoustics,Speech and Signal Processing.Piscataway,NJ:IEEE Press,2013:5583-5587.
[13] 张文旭,陈亚静,陈涛,等.基于FRM的偶型排列信道化改进结构[J].北京邮电大学学报,2016,39(3):27-33.
ZHANG W X,CHEN Y J,CHEN T,et al.Improved structure of even-arrangement channelized based on FRM[J].Journal of Beijing University of Posts and Telecommunications,2016,39(3):27-33(in Chinese).
[14] TSUI K M,CHAN S C,LIM Y C.Design of multiplet perfect reconstruction filter banks using frequency response masking technique[J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers,2008,55(9):2707-2715.
[15] BINDIYA T S,ELIAS E.Metaheuristic algorithms for the design of multiplier-less non-uniform filter banks based on frequency response masking[J].Soft Computing,2014,18(8):1529-1547.
[16] DHABU S,VINOD A P.Design and FPGA implementation of reconfigurable linear phase digital filter with wide cutoff frequency range and narrow transition bandwidth[J].IEEE Tran-sactions on Circuits and Systems Ⅱ:Express Briefs,2016,63(2):181-185.

