航空燃油柱塞泵滑靴副混合润滑特性数值仿真
符江锋, 李华聪, 曾夏青, 刘显为
(西北工业大学 动力与能源学院, 西安 710072)
航空燃油柱塞泵作为发动机喷口油源泵,其工作在发动机机匣外的高温复杂环境中,先进发动机的发展需求使得燃油柱塞泵进一步向高转速、大增压比和强功率负荷的方向发展。滑靴作为柱塞泵的关键摩擦副,长期工作在高速、重载的状态下,其油膜润滑性能是否良好直接制约燃油柱塞泵高压化、高速化并影响柱塞泵性能、寿命及可靠性[1]。
目前,提高摩擦副性能及寿命研究除了发展抗磨材料外,保证其最佳的润滑状态是降低摩擦和减少磨损最普遍、最有效的办法。为此,国内外相关学者针对柱塞泵滑靴副的润滑特性开展了长期而广泛的研究,并取得了显著的理论和试验成果。早期,国外对于轴向柱塞泵滑靴副的相关研究主要集中在滑靴受力、姿态和静压支承润滑特性、滑靴的动力学建模等理论及试验研究方面。近年来,随着数值分析方法和计算机仿真技术的兴起和发展,国外学者越来越多地采取数值计算和软件仿真相结合的方法对柱塞泵关键摩擦副进行研究,典型代表有美国的Purdue大学和德国的亚琛工业大学。Purdue大学的Ivantysynova和Wieczorek等[2-4]基于所设计的CASPAR软件对轴向柱塞泵的配流副、柱塞副和滑靴副3处油膜进行了全面的润滑特性仿真研究;随后又通过CFD软件建立了滑靴副的热弹流动态仿真模型,对高压下的滑靴变形、油膜的温度场进行了数学建模和仿真研究。Ivantysynova和Schenk[5]于2015年在之前研究工作的基础上,建立了滑靴副瞬态热弹性动压润滑模型,该模型涵盖了滑靴的动力学特性、压力场模型、滑靴和斜盘的变形以及滑靴副的热传递模型,是迄今为止最贴近实际情况的一个润滑模型。德国亚琛工业大学IFAS开发了一种可用于建立轴向柱塞泵完整仿真模型的软件DSHplus,该软件可以与多体运动学分析软件ADMAS进行联合仿真来实现滑靴副的动静压仿真。Deeken[6]、Murrenhoff和Wohlers[7]通过ADMAS计算出滑靴副主要部件的动力学参数,与油膜计算模型联合仿真分析滑靴副的瞬态特性。2014年, Deeken等[8]在对滑靴副进行多体运动学仿真的基础上,考虑温度场对滑靴润滑性能的影响并进行了仿真验证。国内对于柱塞泵滑靴副的研究起步较晚,2010—2011年,徐兵和李迎兵等[9-10]用滑靴3点处油膜厚度值对整个滑靴副的油膜厚度场进行了描述,搭建了楔形油膜润滑模型。2011年,刘洪等[11]对轴向柱塞泵滑靴润滑油膜的动态规律进行了数学建模,分析了滑靴润滑油膜与转子转速及柱塞腔压力之间的变化规律。2013年,于思淼[12]重点研究了滑靴副油膜的动压效应和挤压效应,应用MATLAB编制了滑靴副流体动压支承分析软件。2014年,王亚军[13]对求解油膜压力场的有限体积法进行了优化,基于WENO重构计算模型建立了滑靴静压支承自适应分析模型。2013年,魏超等[14]研究了表面微结构对滑靴副油膜承载力和抗倾覆力矩等润滑特性的影响。总体而言,国内对滑靴副的研究还处于初级阶段,在理论研究时对滑靴副做了很多的理想假设,故不能完全真实反映滑靴副的润滑情况。
航空燃油柱塞泵与其他普通轴向柱塞泵相比,其空间结构更加复杂,耦合件精密度要求高,各个组成元件之间的运动和受力关系也要复杂得多。此外,燃油柱塞泵采用低介质黏度的航空3号煤油作为润滑介质,并长期工作在高温度、高压力、高转速恶劣环境中,因此对燃油柱塞泵的摩擦副润滑性能提出了更高的要求,而国内针对航空燃油柱塞泵滑靴仅开展了优化设计和静压支承下的油膜计算分析研究[15-17],尚未开展动静压效应下的滑靴副内部实际润滑分布规律研究。因航空燃油柱塞泵滑靴副多以静压支承原理进行设计,滑靴在斜盘上的运动轨迹是非规则的空间曲线,实际中滑靴将发生倾覆现象,滑靴底面的楔形油膜因为相对运动将产生动压支承力,使滑靴副的压力场分布变得更加复杂。为精确反映滑靴副的内部实际润滑情况,本文在建立航空燃油柱塞泵运动学及动力学模型的基础上,考虑油膜的静压支承及油膜的动压效应,开展了航空燃油柱塞泵滑靴副的润滑特性仿真研究。
1 航空燃油柱塞泵滑靴副动力学与油膜动静压润滑模型
1.1 滑靴副运动学及动力学模型
航空燃油柱塞泵滑靴通常采用阻尼孔型静压支承结构(见图1),即在柱塞腔和滑靴底部油池之间加设一个阻尼小孔(常称进口阻尼)来起调节作用,使滑靴和斜盘在一定的油膜厚度下达到受力平衡。因斜盘工作面为一球面,为保证良好贴合,滑靴底面通常也为一近似球面。由于斜盘表面的曲率半径远大于滑靴副的相关尺寸,为研究方便,后续研究中假设滑靴底面和斜盘表面均为圆形平面。图1中:r1为滑靴底面油池的半径(直径为d1),油池通过直径为d0的阻尼小孔与柱塞腔相通,滑靴工作面外径为d2,h为油膜厚度,FA为沿着轴向方向的正压紧力,p0为中心油池压力,pr为柱塞泵转子腔压力,dz为柱塞直径。
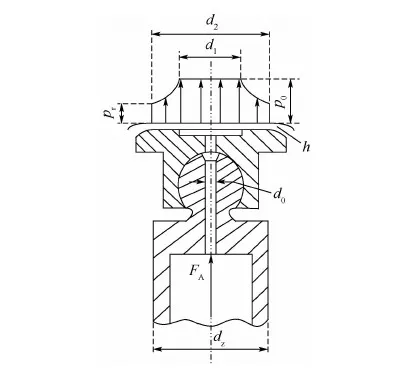
图1 航空燃油柱塞泵滑靴副结构Fig.1 Slipper pair structure of aviation fuel piston pump
航空燃油柱塞泵滑靴通过与柱塞头部形成的球铰副随着柱塞在斜盘表面进行周期运动,其运行轨迹是一复杂的空间曲线。若将滑靴看成一个质点,且同时忽略滑靴运动过程中自身的旋转,则滑靴与柱塞球头中心C的运动情况完全相同。故可以通过分析柱塞的运动来体现滑靴的运动情况,本文中只给出结果,中间详细推导过程略过。滑靴的速度及加速度模型分别如下:
(1)
(2)
式中:A=cosθsinτ;B=-cosτsinθ;θ为柱塞锥顶角;λ=R0/L,R0为斜盘球面中心O1至柱塞锥顶点O的距离;α为转子转角;τ为R0与负X坐标轴的夹角;L为斜盘球面中心O1至柱塞球头中心C的距离;ω为角速度。
柱塞泵高速运转过程中,滑靴受力可从柱塞对滑靴的合力、油膜承载力以及滑靴所受离心力3个方面进行分析,本文中只给出结果,中间详细推导过程略过。柱塞诸多力中沿柱塞轴线和沿滑靴轴线的力将柱塞压向滑靴,使滑靴受到一个沿轴线方向的正压紧力FA,故有
(3)
式中:FL1为柱塞腔内的油压力;Fs1为柱塞弹簧力;Fi为相对运动惯性力;Fcz为离心力沿柱塞轴线的分量;FL2为转子腔内的油压力;Fs2i为保持架弹簧力;ψ为柱塞轴线与滑靴轴线的夹角。
由式(3)可知,由于FA表达式中的各个分量都是转子转角α的函数,故FA也随α作周期变化。
滑靴随柱塞一起绕转子旋转,在斜盘表面的运动轨迹是一条复杂的空间曲线,和柱塞一样,滑靴也受到离心力的作用,若近似认为滑靴离心力作用在滑靴重心Cs上,滑靴在旋转过程中受到的离心力Fcs为
Fcs=msω2(ρ+lGcosψ)sinθ
(4)
(5)
式中:Ff为滑靴副间油膜的黏性摩擦力,也是转子转角α的单变量函数,Ff垂直于柱塞平面,与滑靴在斜盘上的运动方向相反;ms为滑靴质量;lG为滑靴重心到球窝球心C(即柱塞球头中心)的距离;Rs为滑靴的旋转半径;ρ和ψ为转子转角α的函数;μ0为油液动力黏度;r1为中心油池半径;r2为滑靴底面工作半径。
滑靴离心力Fcs随着角度α而变化,其作用在柱塞平面W上,其向垂直于转子轴线向外。
以典型RZB-3型航空燃油柱塞泵为对象,该泵的最大转速n=4 620 r/min,柱塞个数Z=9,柱塞直径dz=16 mm,柱塞锥顶角θ=14°,斜盘角度φ=15.5°,其他结构参数略。通过上述方法对滑靴一个周期内(α从 0°到360°)各个受力进行仿真分析,如图2所示。
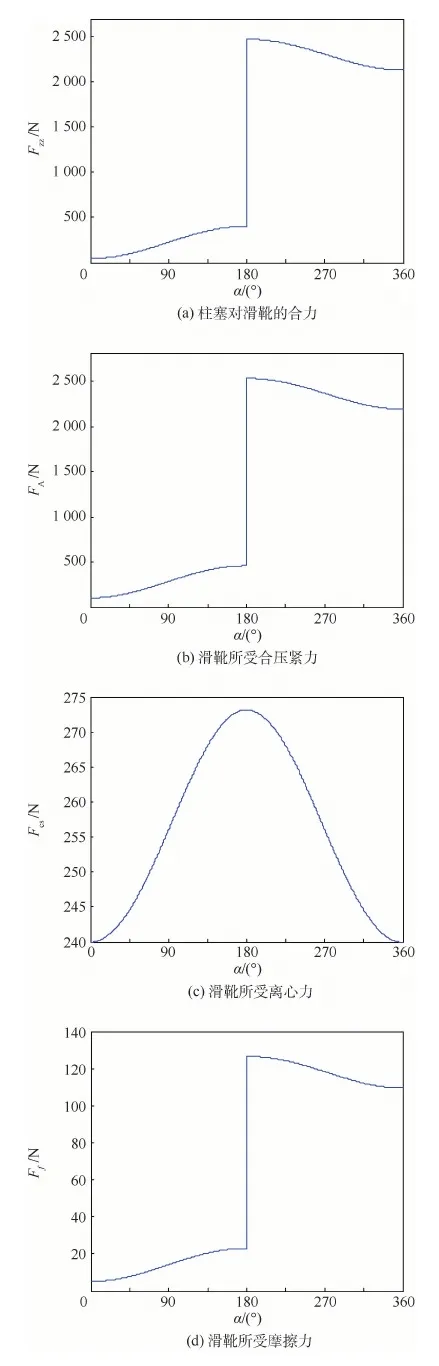
图2 滑靴副受力仿真Fig.2 Force simulation of slipper pair
图2(a)、(b)分别为柱塞对滑靴的合力Fzz以及滑靴所受合压紧力FA,可知滑靴在吸油区受到的合压紧力较小,而在排油区受到的合压紧力可达2 000 N以上。在柱塞泵吸排油切换点(α=180°),柱塞对滑靴的合力和滑靴所受的合压紧力将发生巨变,且在切换点滑靴所受合压紧力最大值为2 532 N。
图2(c)、(d)分别为滑靴所受离心力Fcs和摩擦力Ff的仿真结果,可知滑靴受到的离心力和摩擦力相对于其他力而言较大,对滑靴的运动产生重要影响,在研究滑靴副的润滑特性时需要予以考虑。
滑靴底面的油膜支承力可以分为2个部分。第1部分为中心油池压力p0(0≤r≤r1)产生的支承力,其值为
(6)
第2部分为环形密封带内压力ph(r1≤r≤r2)产生的支承力,通过对密封带内的压力积分可得
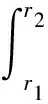
(7)
整个滑靴底面的油膜支承力为
(8)
1.2 油膜动静压润滑模型
通过滑靴副的力平衡和流量守恒建立相应的平衡方程,分别计算滑靴副间油膜的压力分布、滑靴底面环形密封带的燃油泄漏量、滑靴底面油膜支承力和滑靴底面中心油池压力,得出静压支承下的油膜厚度计算模型如下:
(9)
式中:μ为小孔流量系数;ρR为燃油的密度。
由流体力学动压润滑理论[18]可知,滑靴与斜盘之间形成的楔形油膜由于相对运动会产生附加压力场,这是因为流体通过收敛间隙速度增大,产生额外的动压力,从而改变滑靴副油膜静压支承下的压力场分布,并使整个滑靴副的润滑情况变得更为复杂。由于滑靴副油膜的厚度非常小,设定滑靴副油膜为层流,流体黏性和压力在厚度方向保持不变等假设是合理的。在层流状态下,选取柱坐标系为润滑油膜参考坐标系,由于滑靴倾斜方向与运动速度方向并不一致,所以在滑靴径向和周向都有动压产生。根据Navier-Stokes方程和连续性方程,可推导得出柱坐标系下的适合油膜描述的控制方程为
(10)
式中:r为滑靴半径;p为油膜压力;θ*为滑靴坐标系中的角度;η为燃油黏度;vr和vθ分别为滑靴与斜盘相对滑动速度的径向和周向分量;ht和hb分别为滑靴顶部和斜盘底部壁面的厚度。
式(10)即为滑靴副油膜等温不可压黏性定常Reynolds方程。式(10)右边前2项表示油膜在滑靴与斜盘楔形间隙下运动产生的动压效应;中间2项表示由滑靴表面的边界速度梯度引起的变化;后2项表示由滑靴和斜盘的弹性变形引起的油液挤压效应。
2 滑靴副动静压混合润滑特性计算
2.1 基本假设
动压效应的存在使得滑靴副油膜的润滑状况变得错综复杂,其压力场和厚度场的求解也变得更加困难。由于滑靴副间的流动是错综复杂的空间流动,基于滑靴副基本润滑性质分析,研究中对润滑油膜作如下假设:
1) 与黏性力相比,忽略油膜受到的体积力和惯性力,如重力和离心力。
2) 燃油为Newton流体,流动为层流,不考虑油膜中的湍流和涡流。
3) 油液在滑靴副壁面无滑移,即油膜在滑靴底面和斜盘表面的油层速度与壁面速度相同。
4) 在润滑油膜厚度方向上,流体黏性和压力保持不变。
5) 与油膜厚度相比,固体表面的曲率半径很大,因而忽略油膜曲率引起的速度方向的变化。
6) 滑靴副属于窄面密封,假设油膜温度场均匀分布。
2.2 边界条件
边界条件是进行数值求解的重要前提,为求解滑靴副油膜压力分布情况,首先需明确油膜的压力边界条件和速度边界条件。
滑靴副工作时,燃油从中心油池流到柱塞泵转子腔在密封带内形成润滑油膜,故滑靴油膜的内压力边界p1为中心油池压力,外压力边界p2为转子腔压力,即
(11)
又由于油液在滑靴副壁面无滑移,故可知油膜在厚度方向的速度边界条件为
(12)
式中:u为油膜速度的径向分量;v为油膜速度的周向分量。
滑靴副油膜的控制方程为椭圆型偏微分方程,对于这一类方程的求解在现今阶段主要采用有限差分法和有限体积法进行离散,这2种方法在本质上都是基于流体的流量守恒。由相关研究可知,后者在收敛性和求解精度上优于前者,故选取有限体积法求解油膜压力场。有限体积法求解滑靴副油膜压力场的基本过程是由简化的Navier-Stokes方程积分得到油膜的流速方程,沿油膜厚度方向对流速方程进行积分得到单位宽度的截面流量,乘以控制体积的宽度得到整个体积流量,代入流量守恒方程进行求解。具体过程如下:
(13)
式(13)即为不可压缩流体的简化Navier-Stokes方程,将其转化成圆柱坐标形式并在平面上积分可得油膜的流速为
(14)
将式(14)沿油膜厚度方向积分则可得到单位宽度截面上通过的体积流量为
(15)
式中:qr为体积流量的径向分量;qθ为体积流量的周向分量。
通过对滑靴副求解域进行径向和周向网格划分,即将滑靴副润滑区域划分成有限个控制体积,并使每一个体积单元充分得微小以保证后续求解过程中的迭代精度。以每一个网格节点为中心,选取半网格范围空间区域作为离散控制体积。根据流量守恒原理,从各边界流入和流出的流量相等,整个体积内的流量增量为零,即
(16)
利用式(15)即可求出式(16)中的各项流量,如下:
(17)
(18)
(19)
(20)
将式(17)~式(20)代入式(16),并对方程中压力p的偏微分项进行向后差分处理,由此可得到各个节点p(i,j)的数值计算表达式。各网格节点处的离散差分表达式构成了一个非线性方程组,而方程组中的系数都是各个节点待求油膜厚度或油膜压力的函数。本文中采取数值迭代的方法求解上述非线性方程组,从而得到整个油膜的压力分布。
实际求解过程中,先给定初始的中心油膜厚度hc和滑靴最大倾斜角βmax,采用Gauss-Seidel超松弛迭代算法进行求解,并设定数值收敛条件为
(21)
式中:m和n分别为径向和周向网格节点数;ε为从k次迭代到k+1次的相对误差,取[ε]=1×10-6。若迭代误差满足要求,油膜压力场求解完毕,通过积分可求得滑靴副油膜支承力、动压力矩和泄漏量等润滑特性参数。
3 数值仿真分析
3.1 中心油膜厚度和最大倾斜角
基于动静压混合润滑特性求解方法,通过MATLAB编程对滑靴副的非线性动力学模型进行数值求解,可以得到滑靴副一个周期内的中心油膜厚度和滑靴最大倾斜角,其中最大倾斜角取的是绝对值,没有考虑其与坐标系位置的关系,结果如图3和图4所示。
图3中,在考虑油膜动压效应的情况下,滑靴副油膜厚度的变化趋势与静压润滑下的变化趋势大致吻合,但油膜厚度整体上是减小的,且吸排油区切换时油膜厚度不再发生跳变,这正是动压效应的作用,同时也说明只考虑静压支承力求得的油膜厚度是不符合实际的。
由图4可知,滑靴将在吸排油区切换点(α=180°)发生最大倾斜,由动压润滑原理可推出,滑靴在该点将产生最大动压支承力。
若已知滑靴运动周期中某一点的中心油膜厚度和最大倾斜角,在α=180°条件下得到该状况下整个滑靴副的油膜厚度分布,如图5所示。
由图5可知,α=180°时油膜厚度最大值为16.9 μm,最小值为3.1 μm。通过这种求解方式,可得到滑靴旋转周期内任意位置的油膜厚度分布,以及这一位置滑靴底面任意点上的油膜厚度值。

图3 滑靴副中心油膜厚度Fig.3 Central oil film thickness of slipper pair
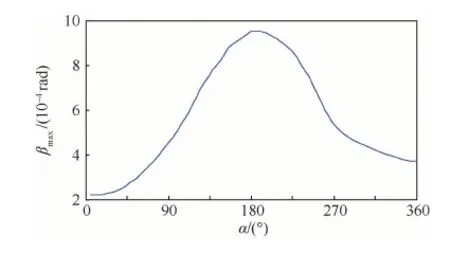
图4 滑靴最大倾斜角Fig.4 Maximum inclination angle of slipper
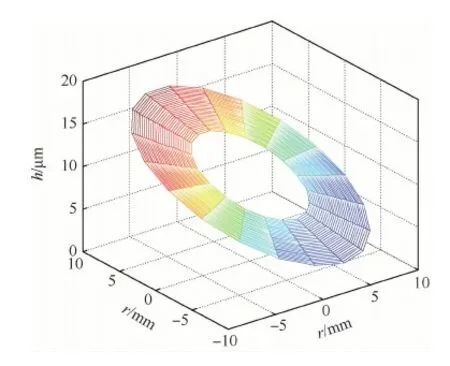
图5 α=180°时的油膜厚度分布Fig.5 Distribution of oil film thickness with α=180°
3.2 影响油膜压力分布的因素
1) 动压效应的仿真验证
取α=180°即吸排油区切换点进行数值模拟,由图3和图4可知此时中心油膜厚度为10.6 μm,最大倾斜角为9.5×10-4rad。按此条件数值模拟得到的结果如图6所示。

图6 实际情况下的油膜压力分布Fig.6 Distribution of oil film pressure in actual situation
为分析该条件下油膜动静压混合支承力中油膜静压支承力和动压支承力的大小,对该情况下的油膜动静压混合支承力进行积分求解,混合支承力为
(22)
其中,油膜的静压支承力为
(23)
油膜的动压支承力为
Fd=Fhd-Fj
(24)
通过式(22)~式(24),得到该时刻的油膜动静压混合支承力即全部承载力为2 509.5 N,其中静压支承力为1 790 N,动压支承力为719.5 N。
为验证动静压混合支承数值模拟计算结果的准确性,将数值计算结果与在滑靴受力计算结果(见图2(b))进行对比。可知在同等条件下,滑靴所受合压紧力为2 532.5 N,动静压混合支承力为2 509.5 N,动静压混合支承仿真计算的支承力较滑靴压紧力相比,相对误差仅为0.9%,表明燃油柱塞泵滑靴副动静压混合润滑分析方法是正确的,且所建立的动静压混合数学模型具有高的计算精度。此外还可以发现,燃油柱塞泵滑靴副动静压混合润滑机理中,油膜的承载力主要由静压支承力提供,但动压支承力同样不可忽略。
2) 中心油膜厚度
滑靴副油膜形状主要由中心油膜厚度和滑靴最大倾斜角确定。在滑靴最大倾斜角下对不同中心油膜厚度的滑靴副油膜压力分布进行了数值模拟。取βmax=7.5×10-4rad,hc=10、11、12 μm,其他仿真参数保持不变,仿真结果如图7所示。

图7 不同中心油膜厚度下的油膜压力分布Fig.7 Oil film pressure distribution under different central oil film thickness
由图7(a)、(b)、(c)对比可知,当滑靴最大倾斜角保持不变时,不同的中心油膜厚度下,滑靴油膜的静压作用区域压力分布几乎不发生改变,动压力峰值随着中心油膜厚度的增加而减小。通过计算可知,油膜整体的静压支承力保持不变,动压支承力则是减小的,但静压力分布随着中心油膜厚度的增加其压力梯度向边缘发散。同时可以直观地发现,油膜的动压效应对于中心油膜厚度的变化十分敏感,在最大倾斜半径上,10 μm中心油膜厚度下的最大压力可达40 MPa以上,1 μm的中心油膜厚度变化可能造成数十兆帕的动压力差值。
3) 滑靴最大倾斜角
取滑靴中心油膜厚度hc为固定值11 μm,滑靴最大倾斜角βmax分别取为6.0×10-4、7.5×10-4rad,其他工作参数保持不变,仿真结果如图8所示。
由图8可知,滑靴中心油膜厚度固定时,随着滑靴最大倾斜角的增加,楔形油膜的收敛性增强,从而促进动压力的产生,使收敛间隙的动压效应更为显著。通过计算动压支承力可知,相比于中心油膜厚度,动压效应对于最大倾斜角的变化更为敏感。同时可以发现,在这一过程中,油膜的静压作用区域压力分布几乎没有发生变化。
对图7和图8分析可知,滑靴副油膜的动压力和静压力是相对独立的,它们之间相互影响较小,且静压作用在滑靴工作过程中更为稳定,在油膜承载力中占主导地位;动压作用虽然贡献更小,但对于滑靴抗倾覆的作用更大。
4) 转子转速
柱塞泵工作时,滑靴随着转子在斜盘表面进行旋转运动,现改变转子转速进行数值模拟。取hc=11 μm,βmax=7.5×10-4rad,转子转速分别为3 000、4 000、5 000 r/min,其他仿真参数保持不变,计算结果如图9所示。
由图9的仿真结果可知,在滑靴相关参数保持不变的情况下,随着柱塞泵转子转速的增加,滑靴在斜盘表面的相对运动速度相应增大,根据动压润滑原理,在相同的收敛间隙下,流体相对于收敛间隙的流速越大,动压效应越明显,产生的动压力也越大。观察各转子转速下油膜的静压作用区域可知,油膜的静压力几乎维持不变。由图9(d)可知,燃油柱塞泵滑靴副在高转子转速下的油膜总承载力大于低转子转速下总承载力,具有更好的润滑效果。
5) 供油压力
滑靴副流体计算域的出口压力即为柱塞泵的供油压力,其在柱塞泵工作时并不是保持恒定的,故有必要对不同供油压力下的滑靴油膜压力分布进行分析。仿真参数为hc=11 μm,βmax=7.5×10-4rad,供油压力分别取10、20、30 MPa,仿真结果如图10所示。
由图10(a)、(b)、(c)可以直观发现,供油压力的增加使滑靴副油膜压力得到了整体提升,无论是体现静压作用的中心压力还是体现动压效应的峰值压力都是随之增大的,但静压支承力随供油压力的增加效果更为显著,油膜的整体承载力随供油压力的增大而提高。由图10(d)中最大倾斜半径为4处即滑靴油池中心的压力值可知,随着供油压力的增加,中心油池压力增加十分明显,且几乎与供油压力大小一致。对上述3种供油压力下的油膜动静压支承力进行计算,结果如图11所示。

图8 不同最大倾斜角下的油膜厚度及压力分布Fig.8 Oil film thickness and pressure distribution under different maximum inclination angles

图9 不同转子转速下的油膜压力分布Fig.9 Distribution of oil film pressure under different rotor speeds
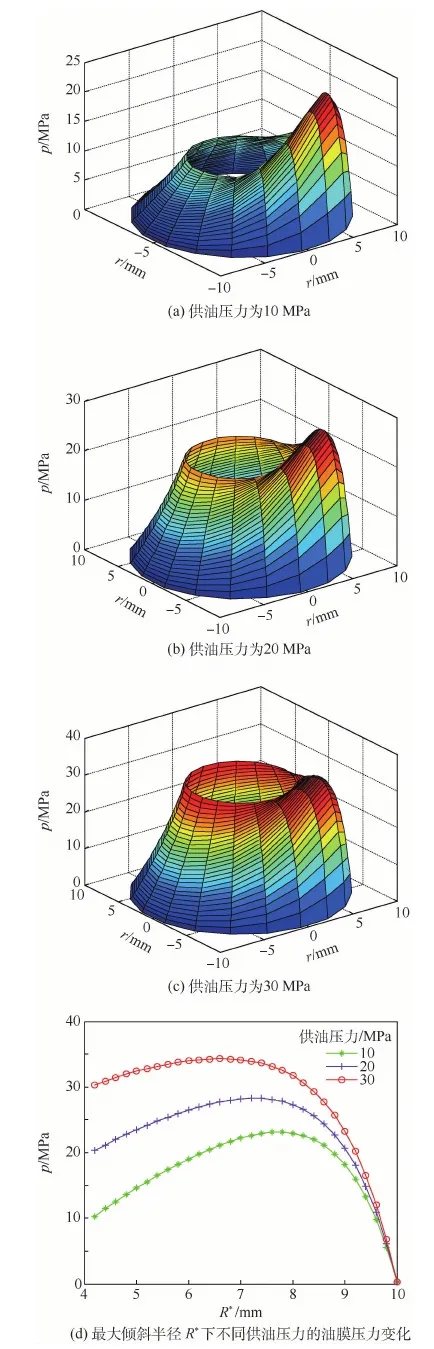
图10 不同供油压力下的油膜压力分布Fig.10 Distribution of oil film pressure under different oil supply pressure
图11中,供油压力的变化对滑靴副油膜的总承载力影响显著,其中主要是对油膜的静压作用影响较大,而动压效应相对比较稳定,动压支承力变化较小。

图11 不同供油压力下的油膜动静压支承力Fig.11 Dynamic and static bearing force of oil film under different oil supply pressure
3.3 结构参数对抗倾覆能力的影响
数值模拟取滑靴底面工作半径r2分别为9、10、11 mm,其他仿真参数与RZB-3型燃油柱塞泵滑靴副仿真时的参数保持一致,取hc=11 μm,βmax=7.5×10-4rad,出口压力为10.29 MPa,进口压力为0.3 MPa,转子转速为4 620 r/min,中心油池半径固定为5 mm,仿真结果如图12所示。
由图12可知,滑靴底面工作半径对滑靴副油膜的压力分布影响很大,随着滑靴底面工作半径的增大,油膜的静压作用区和动压效应区的压力梯度都随之增大,整个油膜的承载力有了很大的提升。通过计算得到不同滑靴底面工作半径下的动静压支承力,如图13所示。
图13可知,静压作用随着滑靴底面工作半径的增大其增强趋势比较缓慢,而动压效应对于滑靴底面工作半径的变化则十分敏感,这一点也可以从图12的最大压力峰值变化得到验证。故可以得到以下结论:通过增大滑靴底面工作半径可以增强油膜的动压效应,从而提高滑靴的抗倾覆能力。
取滑靴底面工作半径为固定值10 mm,中心油池半径r1分别取4、5、6 mm,其他参数不变,数值模拟计算结果如图14所示。
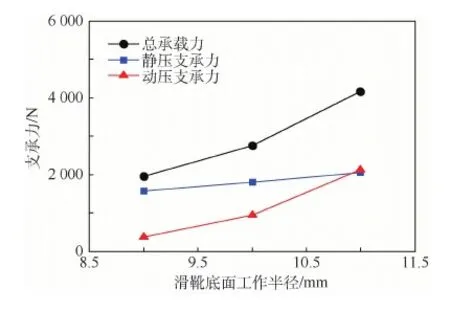
图13 不同滑靴底面工作半径下的油膜动静压支承力Fig.13 Dynamic and static bearing force of oil film under different working radiuses of slipper bottom
从图14的仿真结果可知,中心油池半径对滑靴副油膜压力分布的影响与滑靴底面工作半径类似,不同中心油池半径下油膜的静压作用和动压作用都会发生改变,且动压作用变化更为敏感。同样对该情况下的动静压支承力进行计算,结果如图15所示。
由图15可知,随着中心油池半径的增大,油膜总的承载力有缓慢减小的趋势,这是因为虽然油膜的静压支承力增大了,但动压支承力快速减小,这说明中心油池半径越小,油膜的动压效应越强。

图14 不同中心油池半径下的油膜压力分布Fig.14 Distribution of oil film pressure under different central oil pool radius

图15 不同中心油池半径下的油膜动静压支承力Fig.15 Dynamic and static bearing forces of oil film under different central oil pool radiuses
4 结 论
本文考虑动静压效应对航空燃油柱塞泵滑靴副润滑特性进行了仿真研究,得到以下结论:
1) 滑靴合力的变化对于滑靴副油膜的润滑至关重要,建立滑靴副混合润滑模型时必须考虑滑靴在旋转运动过程中所受到的离心力和摩擦力;对比分析静压润滑和混合润滑机理下的油膜厚度仿真结果可知,动压效应在整个支承力中占28%,因此不可忽略,因动压效应的产生使得动静压混合支承所得到的油膜厚度整体偏小。对比滑靴在α=180°时所受合压紧力与动静压混合支承力计算结果,动静压混合支承力较滑靴合压紧力的计算误差仅为0.9%,表明动静压混合润滑现象应更符合滑靴副实际的润滑状态,且所建立的动静压混合润滑数学模型是可信的。
2) 中心油膜厚度、滑靴最大倾斜角和转子转速是动压效应的主要影响因素,其产生的动压的主要作用在于保障滑靴抗倾覆能力;而滑靴副进口压力即柱塞泵供油压力是油膜的静压作用的主要影响因素,对油膜的静压作用影响占比为62%~85%,但进口压力对动压效应的变化影响甚微。滑靴底面工作半径和中心油池半径对油膜的动压效应影响非常大,其中滑靴底面工作半径增加2 mm,动压效应可增加5.59倍,中心油池半径减小2 mm,动压效应可增加2.67倍。若要提升滑靴的抗倾覆能力,可通过优化以上参数保障滑靴的抗倾覆能力。
参考文献 (References)
[1] 陈永琴.航空燃油柱塞泵运动学与动力学特性分析研究[D].西安:西安电子科技大学,2012.
CHEN Y Q.Analysis of kinematics and dynamics characteristics of aviation fuel piston pump[D].Xi’an:Xi’an Electronic and Science University,2012(in Chinese).
[2] IVANTYSYNOVA M.A new approach to the design of sealing and bearing gaps of displacement machines[C]∥Proceedings of the 4th JFPS International Symposium on Fluid Power.Tokyo:JFPS,1999:45-50.
[3] WIECZOREK U,IVANTYSYNOVA M.Computer aided optimization of bearing and sealing gaps in hydrostatic machine—The simulation tool CASPAR[J].International Journal of Fluid Power,2002,3(1):7-20.
[4] PELOSI M,IVANTYSYNOVA M.Heat transfer and thermal elastic deformation analysis on the piston/cylinder interface of axial piston machines[J].Journal of Tribology,2012,134(4):119-128.
[5] SCHENK A,IVANTYSYNOVA M.A transient thermoelastohydrodynamic lubrication model for the slipper/swashplate in axial piston machines[J].Journal of Tribology,2015,137(3):031701.
[6] DEEKEN M.Simulation of the tribological contacts in an axial piston machine[C]∥ASME 2004 International Mechanical Engineering Congress and Exposition.New York:ASME,2004:71-75.
[7] WOHLERS A,MURRENHOFF H.Tribological simulation of hydrostatic swash plate bearing in an axial piston pump[C]∥Power Transmission and Motion Control Symposium,2007:129-144.
[8] SCHLEIHS C,VIENNET E,DEEKEN M.3D-CFD simulation of an axial piston displacement unit[C]∥9th International Fluid Power Conference,2014:332-343.
[9] 徐兵,李迎兵,张斌,等.轴向柱塞泵滑靴副倾覆现象数值分析[J].机械工程学报,2010,46(20):161-168.
XU B,LI Y B,ZHANG B,et al.Numerical analysis of the phenomenon of sliding pair of axial piston pump[J].Journal of Mechanical Engineering,2010,46(20):161-168(in Chinese).
[10] 李迎兵.轴向柱塞泵滑靴副油膜特性研究[D].杭州:浙江大学,2011.
LI Y B.Axial piston pump slipper oil film characteristics of slide[D].Hangzhou:Zhejiang University,2011(in Chinese).
[11] 刘洪,苑士华,彭增雄.轴向柱塞泵滑靴油膜动态仿真[J].北京理工大学学报,2011,31(11):1282-1286.
LIU H,YUAN S H,PENG Z X.Dynamic simulation of oil film in sliding piston pump[J].Journal of Beijing Institute of Technology,2011,31(11):1282-1286(in Chinese).
[12] 于思淼.轴向柱塞泵用滑靴流体静动压支撑的特性分析及结构优选[D].哈尔滨:哈尔滨工业大学,2013.
YU S M.Characteristics analysis and structure optimization of Slipper with static and dynamic pressure support used in the axial piston pump[D].Harbin:Harbin Institute of Technology,2013(in Chinese).
[13] 王亚军.高压高速轴向柱塞泵滑靴性能研究[D].北京:北京理工大学,2014.
WANG Y J.Research on the performance of high speed axial piston pump slipper[D].Beijing:Beijing Institute of Technology,2014(in Chinese).
[14] 魏超,胡纪滨,薛冰,等.表面微结构对轴向柱塞泵滑靴润滑特性的影响[C]∥第十一届全国摩擦学大会, 2013:1-7.
WEI C,HU J B,XUE B,et al.Effect of surface microstructure on lubrication characteristics of sliding shoe of axial piston pump[C]∥The 11th of Tribology Conference,2013:1-7(in Chinese).
[15] 何必海,孙健国,叶志锋.航空燃油柱塞泵滑靴静压润滑油膜计算分析[J].航空动力学报,2009,24(12):191-197.
HE B H,SUN J G,YE Z F.Calculation and analysis of lubricating oil film of sliding piston for aviation fuel piston pump[J].Journal of Aerospace Power,2009,24(12):191-197(in Chinese).
[16] 何必海,孙健国,叶志锋.燃油柱塞泵滑靴副和配流副油膜计算研究[J].航空动力学报,2010,25(6):1437-1442.
HE B H,SUN J G,YE Z F.Study on the oil film of the slipper pair and the oil distribution pair of fuel injection pump[J].Journal of Aerospace Power,2010,25(6):1437-1442(in Chinese).
[17] 徐佩佩,叶志锋,王彬.航空燃油柱塞泵滑靴油膜的多目标优化设计[J].航空动力学报,2014,29(8):1981-1986.
XU P P,YE Z F,WANG B.Multi objective optimization design of oil film for sliding piston oil pump[J].Journal of Aerospace Power,2014,29(8):1981-1986(in Chinese).
[18] 林硕,苑士华,刘洪.考虑油膜非均匀性的滑靴润滑特性研究[J].北京理工大学学报,2014,34(4):358-362.
LIN S,YUAN S H,LIU H.Study on the lubrication characteristics of sliding shoes considering the heterogeneity of oil film[J].Journal of Beijing Institute of Technology,2014,34(4):358-362(in Chinese).

