一道高考选择题压轴题的多维度解法
李凤迎
(河北省武邑县职教中心 053400 )

A.0 B.mC.2mD.4m
分析本题是全国高考试题选择题最后一道题,作为一道压轴试题,它具有明显的选拔性功能,有很强的区分度.在惜时如金的考场上,能否顺利解出该题,可以说关系着考生个人的前途和命运.因考生的理解能力和解决问题能力的不同,使得对该题的解决方法也会呈现出多种精彩纷呈的思维亮点.充分发掘和利用题目中已知或隐藏的“对称性”,将其作为解决复杂问题的重要突破口,实现解题途径的最佳化.下面我们介绍几种学生比较好理解又便于接受的方法,以供参考.
解法1 特殊函数法

点评根据我们平时所积累的数学经验,我们可以通过将已知抽象函数f(-x)=2-f(x)(x∈R)赋予为我们熟悉的具体函数f(x)=1+x,从而使得较为复杂的问题变得简单化,这正是一种解决问题的快捷有效方法.该种方法简洁明快,易于理解.
解法2 图象平移法
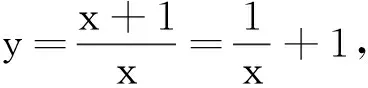
点评这种方法的解题依据是利用函数图象的平移规律.我们知道,图象平移不改变图象的形状.将具有对称性的奇偶函数的图象通过平移就可以获得轴对称型函数图象解题关键是找出平移之前的函数解析式并判断它们的奇偶性,进而判断平移之后的函数图象的交点的横坐标之和和纵坐标之和相对于平移之前的变化情况,进而使得问题得以解决.解题难点是对原函数的分离和对于函数的平移规律的理解.
解法3 中心对称法
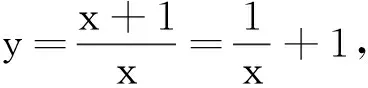
点评这种方法的解题依据是利用函数图象的对称性.解题关键是通过对函数结构的认真观察和思考,找出函数y=f(x)图象的对称中心,进而根据中点坐标公式解决.解题难点是利用f(-x)=2-f(x)对原函数图象的对称中心的寻找和判定.
综上,对函数奇偶性和图象对称特点的考查永远为高考核心考查知识,数形结合和转化思想永远为高考核心思想方法,思维能力和计算能力永远为高考核心解题手段.加强这种方法的练习成为当务之急.
参考文献:
[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心. 普通高中课程标准实验教科书( 必修) 数学4(A 版)[M]. 北京:人民教育出版社,2014.

