一道高三月考试题的解法探究及推广

吴 军

(重庆市武隆中学 408500)

一、问题再现

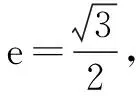
(1)求椭圆C的方程；

(2)直线x=my+1与椭圆C交于P、Q两点，直线A1P与A2Q交于点S,试问：当m变化时，点S是否恒在一条定直线上？若是，请写出这条直线方程，并证明你的结论；若不是，请说明理由.

问题(1)的解答省略.

二、问题(2)的常规解法

解法1 设P(x1,y1),Q(x2,y2),联立

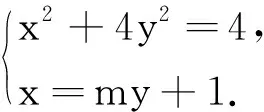
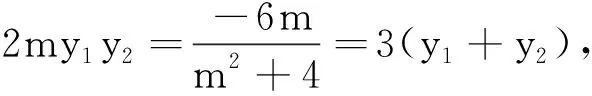
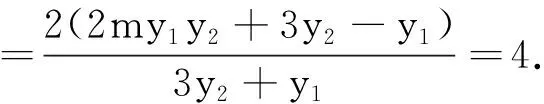
从结果来看，直线x=4=a2这种情形对一般的椭圆方程是否成立，是偶然还是必然？笔者通过探究发现，在一般的椭圆中也有类似性质，进而发现在有心圆锥曲线中也有这一性质.

三、在椭圆中的探究

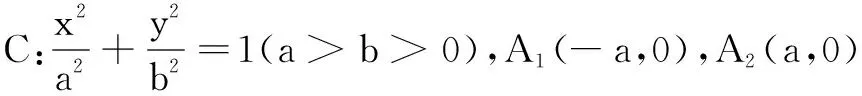
证明设P(x1,y1),Q(x2,y2),联立

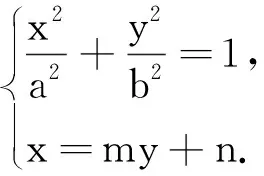
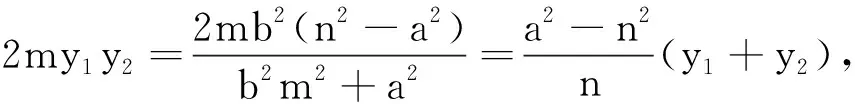
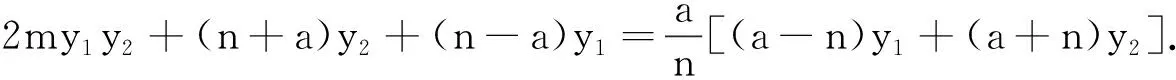
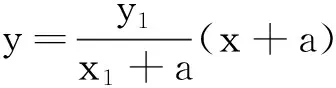
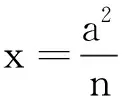
四、有心圆锥曲线的一个优美性质

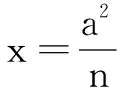
上述优美性质的逆命题是否成立？经过探究发现仍然成立.限于篇幅，不再赘述.

总之，解析几何中像这样可以引申，推广探究的规律有很多，只要经常总结，归纳同类问题的解题方法，并注意探究和发掘变化中所蕴含的一般规律，就会有更多惊喜的收获.

参考文献：

[1]彭朴.对一道高三数学试题的探究[J].上海中学数学，2012(5)：22.

[2]沈辉.对一道高三联考试题的深层次的研究[J].数学教育研究，2013(4)：62.