例谈数学思维的变通性

徐 敏

(江苏省南京行知实验中学 210000)

一、善于运算

运算是数学学习最根本的环节，缺失了运算环节，再简单的问题都无从入手．从当下学生解题的情形来看，教师对于学生运算能力的培养是足够加强的，这从一定程度上简化了学生需要大量思维的时间，可以这么说善于运算是提升思维变通性的第一层次．

例1 已知向量a,b满足|a|=|b|=a·b=2,且(a-c)·(b-2c)=0,求|b-c|的最小值．

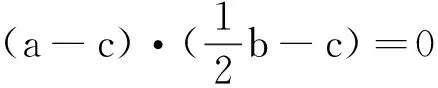
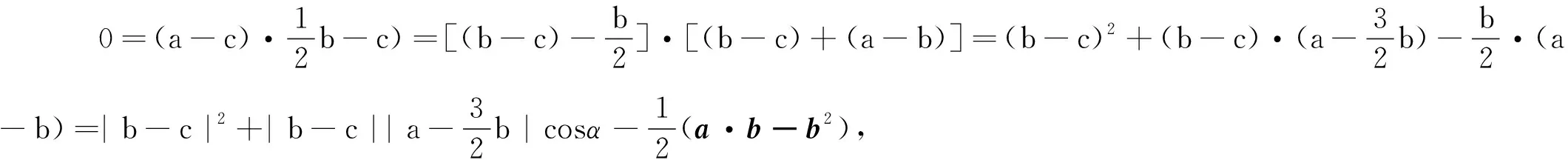
从学生的思维角度来说，任何向量问题的自由性处理，一定是尊崇了向量的本质，但是自由向量难点在于学生较难掌握其运算，这一点对于思维而言并不是太难的点，因此教师要极力从向量数量积自由化的角度引导学生运算，突破这一自由向量的运算还需要整体思想的介入，如|b-c|=x(x≥0)的整体化代换处理．考虑到学生思维可能更为直接，因此正交分解下的坐标代数运算才是最为可能的直接思维.

二、善于转化

学生数学问题不能解决的另一个重要原因，是学生在遇到困难时转化能力的不足，也就是思维不能及时变通．这一困扰一直是中学数学的难点，从解题泰斗罗增儒先生的五十年解题经验来看，其也是这样自我评述的：解题要有积累，要多看多学，这与写文章是一个道理，我解了近五十年的数学题，还要不断学习，初等数学的技巧比较多，陌生问题的解决就是将其不断转化为所学知识，这里需要思维的及时变通，因此多练、多看、多向想是必不可少的．

例2 设实数a,b使方程x4+ax3+bx2+ax+1=0有实根，求a2+b2的最小值．

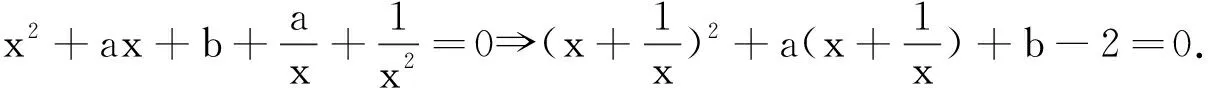
进一步思考，第二层次的转化是什么？自然是如何解决上述转化后方程实根的问题，有比较显著的两个思维视角：

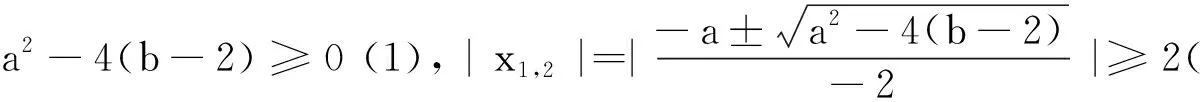
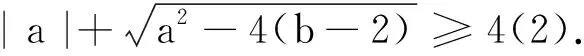
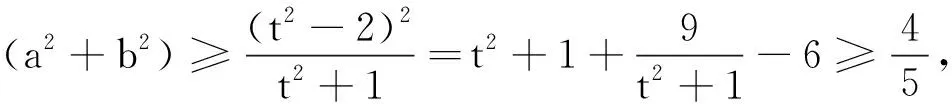
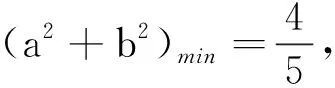
参考文献：

[1]李萍.思维变式教学的尝试[J].数学通讯,2015(11).

[2]金秀青.变式思考——让数学课题更精彩[J].中学数学,2014(6).

[3]邹生书.例谈解题中的思维跳跃[J].数学教学通讯,2015(7).