利用Taylor级数巧妙证明不等式

张铭哲

(山东省日照第一中学 276825)

首先在前面我们将Taylor公式和涉及到的某些不等式列到前面.

1.Taylor定理

若函数f(x)在点a的邻域内有n+1阶导数，则对邻域内一点x存在ξ∈(a,x)或(x,a)使得

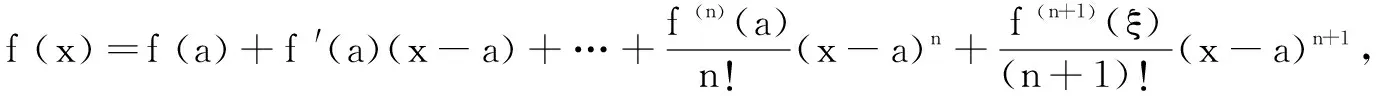
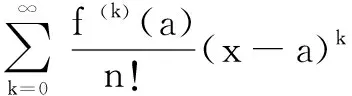
2.Cauchy不等式

ai,bi∈R(i=1,2,…,n)则有

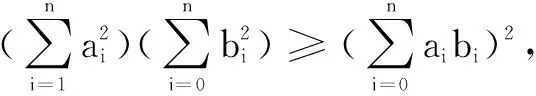
等号在ai,bi成比例时取得.

3.Schur不等式

x,y,z>0,r∈R则

xr(x-y)(x-z)+yr(y-z)(y-x)+zr(z-x)(z-y)≥0.

下面举例说明Taylor级数在不等式证明中的威力.

例1 已知a,b,c∈R+，且a4+b4+c4=3.求证：

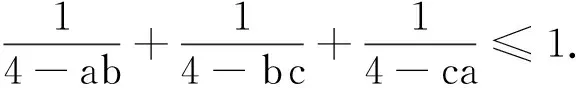
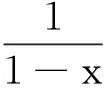
ab+bc+ca≤a2+b2+c2.

故可以将每项都展成 Taylor 级数来证明.

证明易知ab,bc,ca<4.

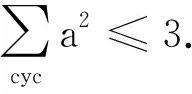
例2 已知a,b,c∈(0,1)，求证:

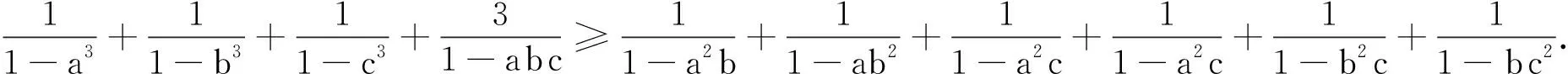
分析两边作差后有明显的 Schur 不等式的形式，但变量都在分母上，难以直接应用 Schur 不等式.可以考虑用 Taylor 展开将每项都化成幂级数，巧妙地去掉分母，然后再用 Schur 不等式完成证明.

证明因a,b,c∈(0,1) 故原不等式等价于

又原不等式两边均收敛，故此级数亦收敛.由 Schur 不等式知此级数每项均非负，故总和非负.进而原不等式成立.

例3 当正实数a,b,c满足a+b+c=1.求证：

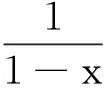
故只需证：

由 Muirhead 定理：

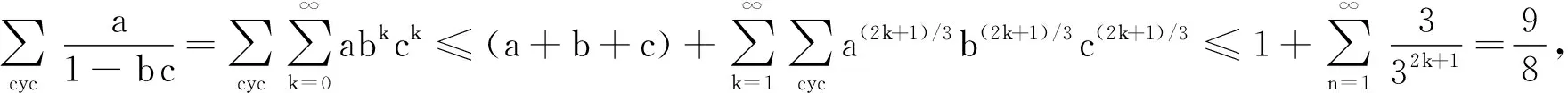
例4 设a,b,c是正实数，且满足abc=1.求证:

分析本题没有明显的可以运用 Taylor 展开的特征，但利用abc=1升次之后得

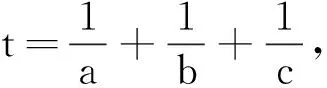
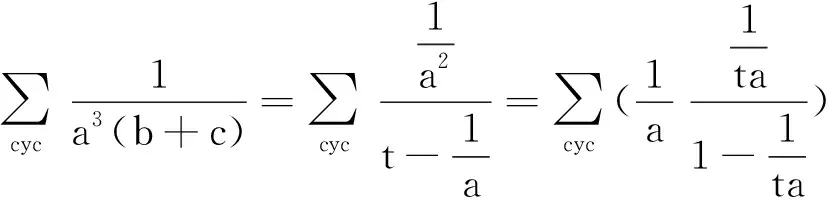
例5 已知x,y,z是正实数，求证：

coshx2+coshy2+ coshz2≥coshxy+coshyz+coshzx

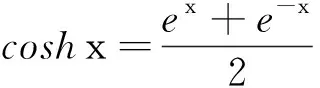
分析本题涉及超越函数，除 Jensen 不等式外的常见不等式很难处理这种类型的题.但稍做尝试便知道 Jensen 不等式做此题也是不够的，但利用 Taylor 展开可以给一个相当漂亮的证明.

证明由题意得：

注用相同的方法，对双曲正弦也可以得到类似的不等式：已知x,y,z是正实数，

则sinhx2+sinhy2+sinhz2≥sinhxy+sinyz+sinhzx.

由上面几例可以看出，可以运用 Taylor 级数解决的不等式问题往往有比较明显的特征，易于发现.而且运用 Taylor 级数最明显的一个特点就是该方法能在不放缩的情况下将分式不等式、超越不等式转化为有关多项式的不等式，方便利用幂平均不等式、Cauchy 不等式等不等式，这在一定程度上降低了直接利用这些不等式导致放缩放过的可能性.

对某些分式不等式，虽然看起来并不适用于这种方法，但往往稍作代换就可以整理成比较好的形式，进而可以利用 Taylor 级数给出一个简单而美妙的证明.

参考文献：

[1]陈计,季潮丞.数学奥林匹克命题人讲座:代数不等式[M].上海：上海科技教育出版社,2009.

[2]陈天权.数学分析讲义:第一册[M].北京：北京大学出版社,2009.

[3]刘初喜,施洪亮.华东师范大学第二附属中学数学教材:下册[M].上海：上海教育出版社,2012.