基于伪四维投射坐标的多基链标量乘法

徐明，史量

（1. 上海海事大学信息工程学院，上海 201306；2. 同济大学电子与信息工程学院，上海 201804）

1 引言

公钥密码体制是密码学的重要组成部分。目前基于公钥密码体制的密码系统主要有 RSA密码系统[1]和椭圆曲线密码系统[2,3]（ECC, elliptic curve cryptosystem）。近年来，随着分布式计算以及量子技术的日趋成熟，对密码系统的安全性要求也急剧提升，导致 RSA密钥长度随着保密性提高而迅速增长的缺点被不断放大。这使密钥长度较短的椭圆曲线密码系统的应用领域越来越广，在无线传感器网络[4]、智能芯片卡[5]以及虚拟货币[6]的加密中都有比较成熟的应用。美国国家安全局建议，384位椭圆曲线密码系统足以保护美国军方最高机密[7]。

然而，椭圆曲线密码系统的高安全性是建立在“黑盒攻击”[8]的基础上的，即攻击者只知道算法的输入和输出，而对算法的内部构造一无所知。实际上，加密设备在运行过程中不可避免地会泄露一些侧信道信息[9]。Kocher[10]在1996年提出可以通过侧信道泄露的信息，如运算过程中各部分所用时间、电磁辐射量和消耗能量不同等信息，分析出保密信息的攻击方法，使一些在数学理论上安全的加密手段也有被破解的可能。对于通过椭圆曲线密码系统加密的单片机系统，由于其加密系统在运行时功耗噪声较小以及椭圆曲线密码系统在标量乘运算中的相关特性，特别容易受到能量分析攻击的威胁[11]。能量分析攻击可以分为简单能量分析（SPA, simple power analysis）攻击[12]和差分能量分析（DPA, differential power analysis）攻击[13]。

为了提高椭圆曲线密码系统的整体效率和安全性，目前，主流方法从多个结构层次对其进行优化。文献[14]指出，在传统雅可比坐标下，倍点运算开销为4M+6S，其中，M为乘法运算，S为平方运算，三倍点运算开销为 6M+10S，五倍点运算开销为15M+10S；文献[15]使用侧信道原子法，在群运算层抵御SPA，并且通过引入第四变量W简化群运算，使倍点运算的开销降低到6M+4S。文献[16]在标量乘运算层采用经过随机基点坐标处理的蒙哥马利阶梯法，可以抵御SPA和DPA，并根据蒙哥马利阶梯法的特点设计了复合群运算，将点加和倍点的整体开销降低到6M+5S。文献[17]在使用NIST曲线的基础上，将倍点运算的开销降低到4M+4S，并且在标量乘运算层上改进了D&A（double and add）方法，使其系统可以抵御SPA和DPA。文献[18]的方法与文献[16]类似，使用MoTE曲线并改进了投射坐标，将点加和倍点的整体开销降低到5M+4S。文献[19]在标量乘运算层采用以2、3为基的双基链法，在群运算层通过完全平方变换将倍点运算和三倍点运算的开销分别降低到1M+8S和5M+10S。文献[20]在标量乘运算层采用以 2、3、5为基的多基链法，并且引入最小值系数c1、c2、c3缩短基链长度，在群运算层加入变量U去除Y3的冗余运算，与完全平方变换相结合，使五倍点运算的开销降低到12M+13S。文献[21]利用二元域下域运算层求逆运算消耗较小的特点，在群运算层中使用仿射坐标系，同时在标量乘运算层中加入半点进行多基运算，使系统整体效率相比其他通用算法提高了3.91%～45.16%。由于椭圆曲线密码系统经常应用到一些计算能力较低的系统中，并且许多应用场景无法被开销较低的对称加密所代替（如信用卡身份验证）。因此，提高椭圆曲线密码系统的运算效率显得非常重要。运算效率的提高意味着单片机系统可以运行的密钥长度更长，即安全性更高。此外，由于文献[17,18]使用了特殊椭圆曲线，文献[16,21]仅适用于二元域，因此应用场景具有局限性。

针对上述问题，本文在保证安全性的前提下，通过对椭圆曲线密码系统进行分层优化来提高椭圆曲线密码系统的整体效率。该方案兼容二元域和素数域，适用于任意椭圆曲线。针对群运算层，本文提出基于伪四维坐标的群运算，通过在标准雅可比坐标上引入新参数aZ4，使坐标由(X,Y,Z)变为(X,Y,Z,aZ4)，实现对群运算的优化，并推导出基于伪四维投射坐标的倍点运算、三倍点运算、五倍点运算的计算式和算法。针对标量乘运算层，本文对多基链生成算法中的贪心策略进行优化，提出最短链存在定理，并由最短链存在定理推导出最短链表，得出160、192、256和384位密钥中最小值系数c1、c2、c3的最优值。在安全性方面，本文通过平衡能量法与Masking方法相结合的方式，可以成功抵御SPA和DPA等常见能量分析攻击。

2 基础知识与相关工作

2.1 有限域中的椭圆曲线

椭圆曲线密码系统基于椭圆曲线的离散对数问题，通常使用有限域内的曲线。一般最常用的有限域是素数域GF(p)和二元域GF(2m)。素数域兼容性较高，几乎适用于所有椭圆曲线密码系统的应用，而在FPGA等单片机环境中，二元域有着较高的运算效率。

在运算效率方面，素数域和二元域最大的区别在于域运算中求逆运算的效率。素数域求逆运算消耗大约相当于 80～100次乘法运算[18]，所以通常采用雅可比投射坐标消除求逆运算。而二元域求逆运算效率相比素数域有很大提高，消耗仅为 8～10次乘法运算[21]，所以通常在群运算层采用仿射坐标，并且在标量乘运算层采用连续相同群运算的方法（如双基链或多基链法）以减少求逆运算。

2.2 椭圆曲线密码系统的层次结构

椭圆曲线密码系统可分为5层：物理层、域运算层、群运算层、标量乘运算层和应用层，如图 1所示，其中，上层运算依赖于下层运算，而下层运算为上层运算提供服务。

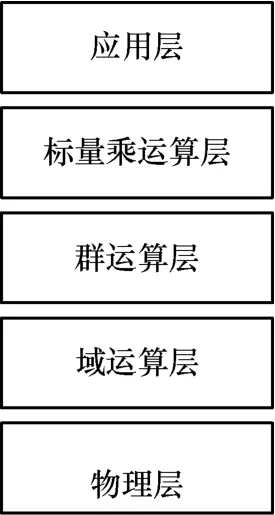
图1 椭圆曲线密码系统层次结构

2.2.1 域运算层

域运算又称原子运算，是有限域上最基本的运算，即模运算。椭圆曲线密码系统会用到5种基本的域运算——加法、取负、平方、乘法、求逆。文献[22]中指出在分析算法效率时，加法、取负运算因为运算消耗相较其余3种运算微乎其微，基本可以忽略，所以在分析效率时只需讨论平方、乘法、求逆的运算次数。

2.2.2 群运算层

椭圆曲线在素数域上的点可以组成一个循环群。对于椭圆曲线上的任意两点，一定存在该椭圆曲线上的第三点为两点之和。图2描绘了椭圆曲线群运算的几何意义。

定义 1 如果椭圆曲线上三点共线，则它们的和为O，其几何意义是无穷远点[22]。

由定义1可以推导出椭圆曲线上的加法定律。1)O为加法单位元，即P+O=O+P=P。

2) 设R1=(x,y)是椭圆曲线上的点，根据x轴对称性可知，R2=(x,−y)也是椭圆曲线上的点，可以看作R1、R2与无穷远点三点共线，所以R1+R2+O=O，即R1=−R2。

3) 通过1)和2)可以看出，若椭圆曲线上P、Q、R三点共线，则椭圆曲线上相异两点P、Q之和为−R，即P+Q=−R，几何意义如图2(a)所示。

4) 将3)中的Q无限逼近P，当P、Q重合时，直线PR为椭圆曲线上的切线，即2P=−R，几何意义如图2(b)所示。

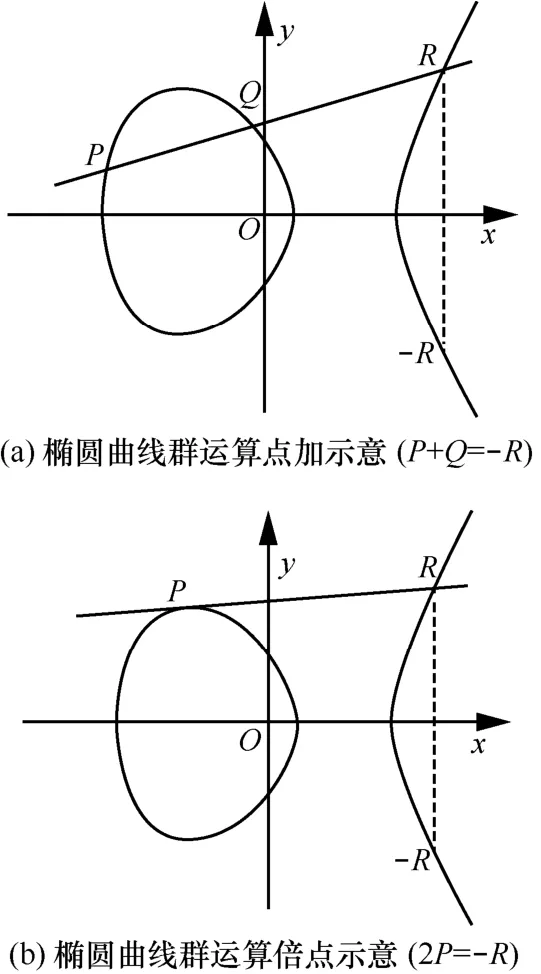
图2 椭圆曲线群运算几何意义示意

上述3)和4)构成了椭圆曲线群上的2个基本运算：点加和倍点。

2.2.3 标量乘运算层

标量乘运算是椭圆曲线密码系统最主要且消耗能量最大的运算。椭圆曲线的基本群运算只有点加和倍点。如果要实现乘法运算，必须将乘法运算转换为点加和倍点的组合。椭圆曲线密码系统常见的标量乘法有D&A法[17]、NAF法[23]、蒙哥马利阶梯法[16,18]、双基链标量乘法[19]和多基链标量乘法[14,20]。多基链标量乘法的原理如式(1)所示。

其中，为基的个数，n为链长，{bj}为单调递减数列。

从式(1)可以看出，在椭圆曲线标量乘法中，使用多基链法计算kP，只需依次进行bj次aj倍点运算，然后再进行n次点加，即可求出点Q。由此可知，多基链标量乘法的优化原则为：

1) 尽可能提高aj倍点的运算效率；2)b1尽可能小；

3) 链长n尽可能短。

针对上述原则，本文通过基于伪四维投射坐标的快速群运算和基于伪四维投射坐标的多基链标量乘法，对椭圆曲线密码系统进行分层优化。

2.2.4 应用层

应用层搭载着基于椭圆曲线密码系统的众多应用，如基于椭圆曲线的密钥交换和基于椭圆曲线的数字签名等，这些都是椭圆曲线密码系统的经典应用。

3 基于伪四维投射坐标的快速群运算

3.1 伪四维投射坐标的建立

在2.1节中，群运算的优化原则是去除求逆运算，尽量减少乘法运算，平方运算可以适当增加。雅可比投射坐标相比仿射坐标增加了一个维度，将二维变为三维，从而达到优化运算的目的。由于雅可比坐标下的倍点、三倍点和五倍点计算式中有多个aZ4，若可以将aZ4通过变换获得，则可以进一步优化倍点的效率。伪四维投射坐标正是利用该原理，在雅可比投射坐标上加一个维度参数aZ4，由(X,Y,Z)变为(X,Y,Z,aZ4)。由于坐标中第三个和第四个参数并不独立，因此它不是真正的四维坐标，本文将其称为“伪四维”。

文献[15]在改进雅可比坐标的基础上提出了一种基于侧信道原子法的群运算。该方法通过将群运算拆分为若干个拥有相同的运算顺序和结构的运算单元，达到抵御SPA的目的。而本文在标量乘运算层中使用平衡能量法和Masking方法抵御SPA和DPA，因此在群运算层不需要考虑侧信道攻击，使群运算效率得到进一步提升。此外，基于伪四维投射坐标的群运算并没有用到特殊曲线（如NIST曲线[17]、MoTE曲线[18]和Edwards曲线[19]）的性质，所以适用于所有的椭圆曲线。5.1节群运算效率分析实验表明，伪四维投射坐标在素数域和二元域下的性能均高于对照算法，所以适用于二元域和素数域，具有良好的兼容性。

3.2 基于伪四维坐标的倍点运算

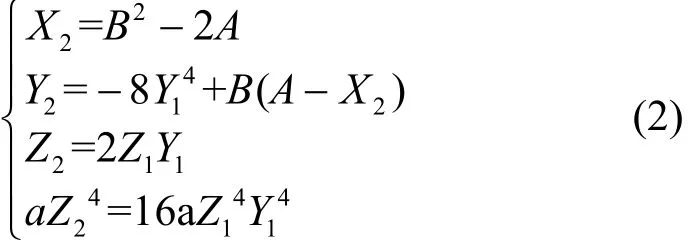
其中，

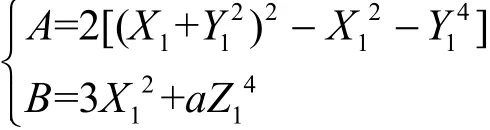
算法1 基于伪四维坐标的倍点运算

输入

输出

初始化

1)

返回由算法1可以得出，基于伪四维坐标的倍点运算需要的域操作数为3M+5S。

3.3 基于伪四维坐标的三倍点运算

其中，

算法2 基于伪四维坐标的三倍点运算

输入

输出

初始化

1)

2)

3)

4)

返回

由算法2可以得出，基于伪四维坐标的三倍点运算需要的域操作数为7M+7S。

3.4 基于伪四维坐标的五倍点运算

其中，

根据式(4)，可以得出如图3所示的伪四维投射坐标五倍点运算的域运算示意。其中，表示加法，表示自取负表示平方，表示乘法。图 3从输入最 后 从输 出由图3可以计算出基于伪四维

投射坐标的五倍点运算需要的域操作数为11M+12S。

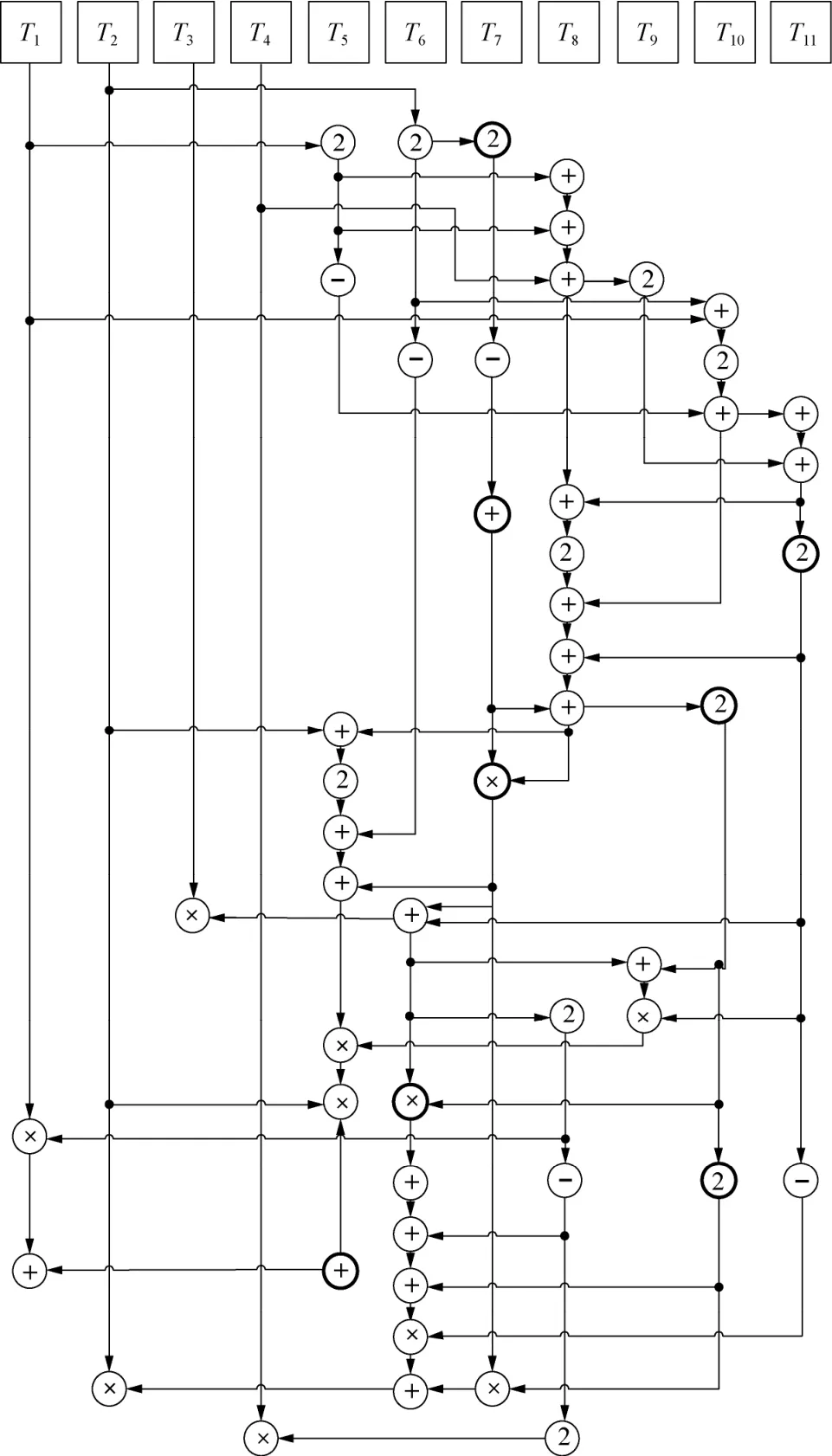
图3 伪四维投射坐标五倍点运算的域运算示意

4 基于伪四维投射坐标的多基链标量乘法

4.1 多基链生成算法的优化策略

文献[20] 提出了一种以2、3、5为基的多基链生成算法，将大整数k化为以2、3、5为基的和，即。若保证{bin}、{tri}和{pen}为单调递减数列，则可以提取公因式，简化计算。具体实现过程如算法3多基链生成算法[20]所示。

算法3 多基链生成算法

输入 大整数k，倍点最大值maxb，三倍点最大值maxt，五倍点最大值maxq，最小值系数c1,c2,c3

输出

1) if maxb=0&&maxt=0&&maxq=0then

2) returnk

3) end if

4)bin= maxb×c1

5)tri= maxt×c2

6)pen= maxq×c3

7) 通过贪心算法找到最合适的整数| |k−num和bin、tri、pen

8) ifk＞numthen

9)si=1

10) else

11)si=−1

12) end if

13) ifnum＞0 then

14)多基链生成算法(|k−num|,bin,tri,pen,c1,c2,c3)

15) end if

16) returnk

算法3中设置了倍点、三倍点和五倍点的最大值，并且每一次都将求出来的倍点、三倍点和五倍点个数代入下一次递归，保证多基链是递减的，方便接下来的标量乘运算。此外，为了防止基链过于冗长，算法 3引入了最小值系数c1、c2、c3来限制倍点、三倍点和五倍点个数的最小值来提高标量乘算法的运算效率。其数学模型如式(5)所示。

已知

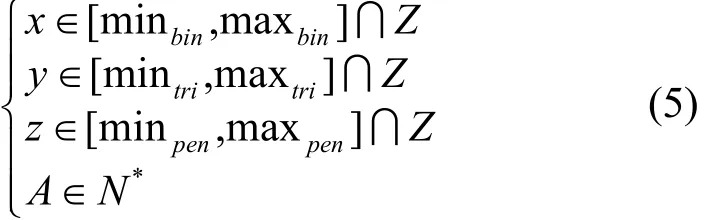
求min(|A−axbycz|)以及此时满足条件x、y、z的取值。其中，a,b,c∈N*为基，minbin,mintri,minpen,maxbin,maxtri,maxpen为已知常数。

可以看出，该策略保证了在文献[20]的约束条件下，其多基链的链头最大。然而，由于倍点、三倍点以及五倍点的群运算开销不同，所以链头最大并不能保证整个系统的开销最小。同时，若要实现算法3，关键在于如何求得min(|A−axbycz|)以及x、y、z的值，但文献[20,21]均没有提及相应方法。如果采用枚举法实现该算法，则时间复杂度为O(n× maxbin× maxtri× maxpen)，且大整数乘方运算相当复杂，所以该运算会消耗大量的运算资源。文献[24]提出使用图结构解决双基链的贪心算法问题。为了在双基链中找到最合适的|k−num|，对应算法3第7行的时间复杂度为O((logn)2)。如果应用到多基链中，则算法3的时间复杂度为O(n(logn)3)。虽然该方法比枚举法的时间复杂度明显降低，但由于大整数运算非常复杂，所以该时间复杂度仍然不够理想。

针对以上问题，本文使用拉格朗日乘数法建立数学模型并对算法3中的贪心算法进行优化，找到最合适的倍点、三倍点和五倍点个数。首先，给出数学模型如下。

已知

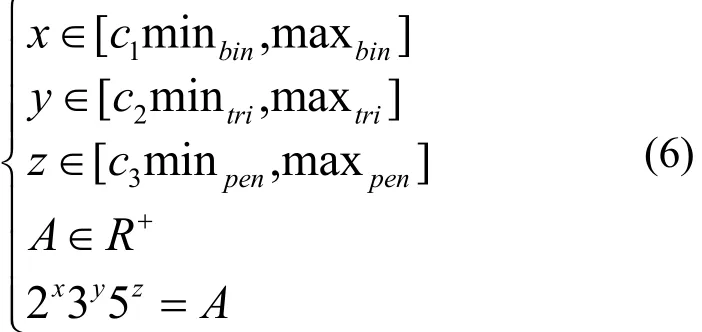
求min

其 中 ，c1、c2、c3为 (0,1)的 已 知 常 数 ，minbin,mintri, minpen,maxbin,maxtri, maxpen也为已知常数。根据拉格朗日乘数法，得到拉格朗日方程组为

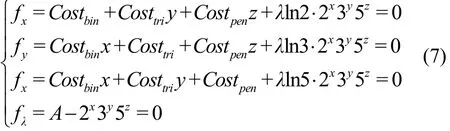
将相关约束条件加上，若l、m、n超出取值范围，则取其范围内的最值；若l、m、n在取值范围内，则分别将l、m、n进行上下取整，最多可以得到=20种组合，并选择min(Costbinx+Costtriy+Costpenz)为最终取值。

上述优化将原本以链头大小为优先的贪心策略变为以开销为优先的贪心策略，使系统整体开销减小。理论上，通过建立基于拉格朗日乘数法的优化策略，可以将多基链生成算法的时间复杂度降为O(n)，提高了系统的整体效率。

4.2 最短链存在定理和最短链表

在本文提出的多基链生成算法的优化策略中，用到了最小值系数c1、c2、c3。本节将通过最短链存在定理证明调整最小值系数c1、c2、c3可以使链长最短。此外，通过运算给出常见密钥位数的最短链长以及最小值系数c1、c2、c3的取值，在实际应用中可以通过该表快速获取最适合的最小值系数c1、c2、c3。

4.2.1 最短链存在定理

定理 1 以 2、3、5为底的多基链，∃c1,c2,c3∈ (0,1)，使多基链的链长最短。

证明 根据算法3，可以将定理1抽象为函数

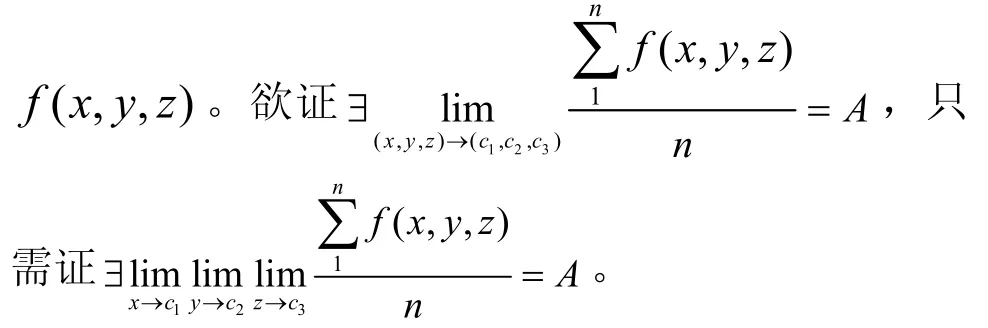
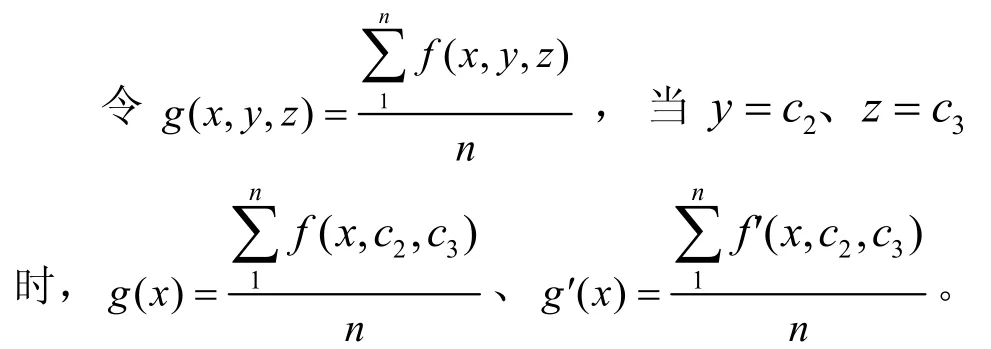
由于通过算法3的贪心算法可以找到最适合的bin、tri、pen，所以一定∃x=c，使g'(x) = 0；根据对称性，y、z同理。所以，多元函数g(x,y,z)一定存在驻点，即证毕。

4.2.2 最短链表

定理1证明了最短链的存在，并且证明了最短链的三重极限可化为累次极限，所以可以通过计算机进行无限逼近求得当链长达到最短极限的c1、c2、c3，得到如表1所示的最短链表。

表1 最短链表

4.3 基于伪四维投射坐标的多基链标量乘法

算法4详细描述了本文提出的基于伪四维投射坐标的多基链标量乘法。

算法4 基于伪四维投射坐标的多基链标量乘法

输入 整数bin1≥bin2≥…≥binm≥0，tri1≥tri2≥…≥trim≥0，pen1≥pen2≥ …≥penm≥ 0；基点P∈E(Fp)。

输出Q=kP∈E(Fp)

1)R←random()//生成E(Fp)上的随机点

2)Q←基于雅克比坐标点加(P,R)

3)Q'←Q

4)u←binm

5)v←trim

6)w←penm

7) fori=m−1 to 1 do

8) forj=1 towdo

9)Q'←基于伪四维坐标五倍点(Q')

10) end for

11) fork=1 tovdo

12)Q'←基于伪四维坐标三倍点(Q')

13) end for

14) forl=1 toudo

15)Q'←基于伪四维坐标倍点(Q')

16) end for

17)Q''← 求逆(Q')

18) ifsm−i+1= 1 then

19)Q←基于雅克比坐标点加(Q,Q')

20) else

21)Q←基于雅克比坐标点加(Q,Q'')

22) end if

23)u←bini−bini−1

24)v←trii−trii−1

25)w←peni−peni−1

26) end for

27)R← 求逆(R)

28)P←基于雅克比坐标点加(Q,R)

29) returnP

在算法4中，由于多基链中每一个节点的次数都是单调递减的，所以可以保证整个算法的倍点、三倍点和五倍点个数为bin1、tri1和pen1。此外，倍点、三倍点和五倍点运算采用伪四维投射坐标，点加运算采用雅可比坐标。为了抵御DPA攻击，算法4对基点P采用Masking方法进行了处理：在算法的第1行和第2行将基点P加上随机点R，然后在算法 4的第 27行和第 28行将结果还原，即kP= (kP+R)−R。由于这里的R是随机的，每次运行的能量分析曲线也是随机的，无法进行DPA攻击。为了抵御SPA攻击，算法4的第17行先计算Q''，从而在第 18～第 22行中，无论sk= 1或sk=−1，都进行一次点加，使能量平衡，攻击者无法通过波形获取si的取值，从而达到抵御SPA攻击的目的。

5 系统效率分析与实验

5.1 群运算效率分析

椭圆曲线群运算作为标量乘运算的底层，对系统效率起到了决定性作用。本节将基于伪四维投射坐标的群运算效率与其他算法进行对比，结果如表2所示。其中，N/A表示文献中没有涉及，I表示求逆运算。

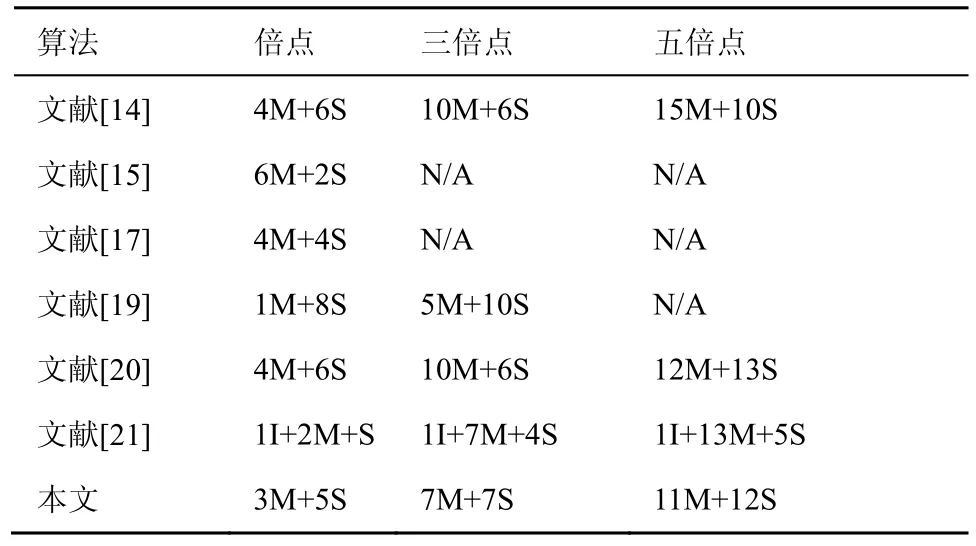
表2 群运算效率比较

5.1.1 离散群运算效率比较

文献[18]指出，素数域中求逆运算的消耗非常大，当密钥长度为 160位时，其运算开销为11M+158S。所以使用雅可比投射坐标消除求逆运算是基于素数域的椭圆曲线密码系统的主流做法。文献[17, 19, 20]以及伪四维投射坐标均为雅可比投射坐标的进一步优化。

文献[14]指出，素数域中的平方运算与乘法运算开销的比值S/M为0.8，由表2可以看出，对比标准雅可比投射坐标，伪四维投射坐标倍点运算的开销降低了 26.67%，三倍点运算的开销降低了21.43%，五倍点运算的开销降低了15.38%。

相比其他算法，对于倍点和三倍点运算，对照表2中开销最小的文献[19]，伪四维投射坐标比文献[19]倍点运算开销降低了 5.71%，三倍点运算开销降低了3.17%；对于五倍点运算，对比表2中开销最小的文献[20]，伪四维投射坐标比文献[20]五倍点运算开销降低了8.74%。

5.1.2 连续群运算效率比较

二元域中的求逆运算较素数域的求逆运算有较大优势，其求逆运算的开销从素数域中80～100次乘法减少为 8～10次乘法，开销降低了10倍[21]，并且在文献[21]的多基链运算中，连续的倍点、三倍点和五倍点运算较多，群运算可以进一步简化，所以文献[21]使用了仿射坐标而非雅可比坐标。从表2中不难看出，k越大，文献[21]的群运算效率越高。图 4刻画了随着k增大文献[21]的仿射坐标和本文伪四维投射坐标群运算效率的对比效果。

如图4(a)所示，在三倍点运算中，伪四维投射坐标的运算开销均低于仿射坐标，并且当k增大时，优势更为明显。当密钥长度为160位时，根据实验样本统计，k的数学期望= 15.771，所以根据表2，在仿射坐标下的期望开销= 240.794，而在伪四维投射坐标下的期望开销= 176.635。由此可得，在二元域中伪四维投射坐标下的三倍点运算比仿射坐标下的三倍点运算开销降低了36.32%。同理，如图4(b)所示，在五倍点运算中，虽然从图4中伪四维投射坐标看似优势并不明显，但密钥长度为160位时，k的数学期望= 5.738，根据表2中文献[21]的连续五倍点式，在仿射坐标下的期望开销= 122.622，而在伪四维投射坐标下的期望开销= 104.432。由此可得，在二元域中伪四维投射坐标下的五倍点运算比仿射坐标下的五倍点运算开销降低了17.42%。

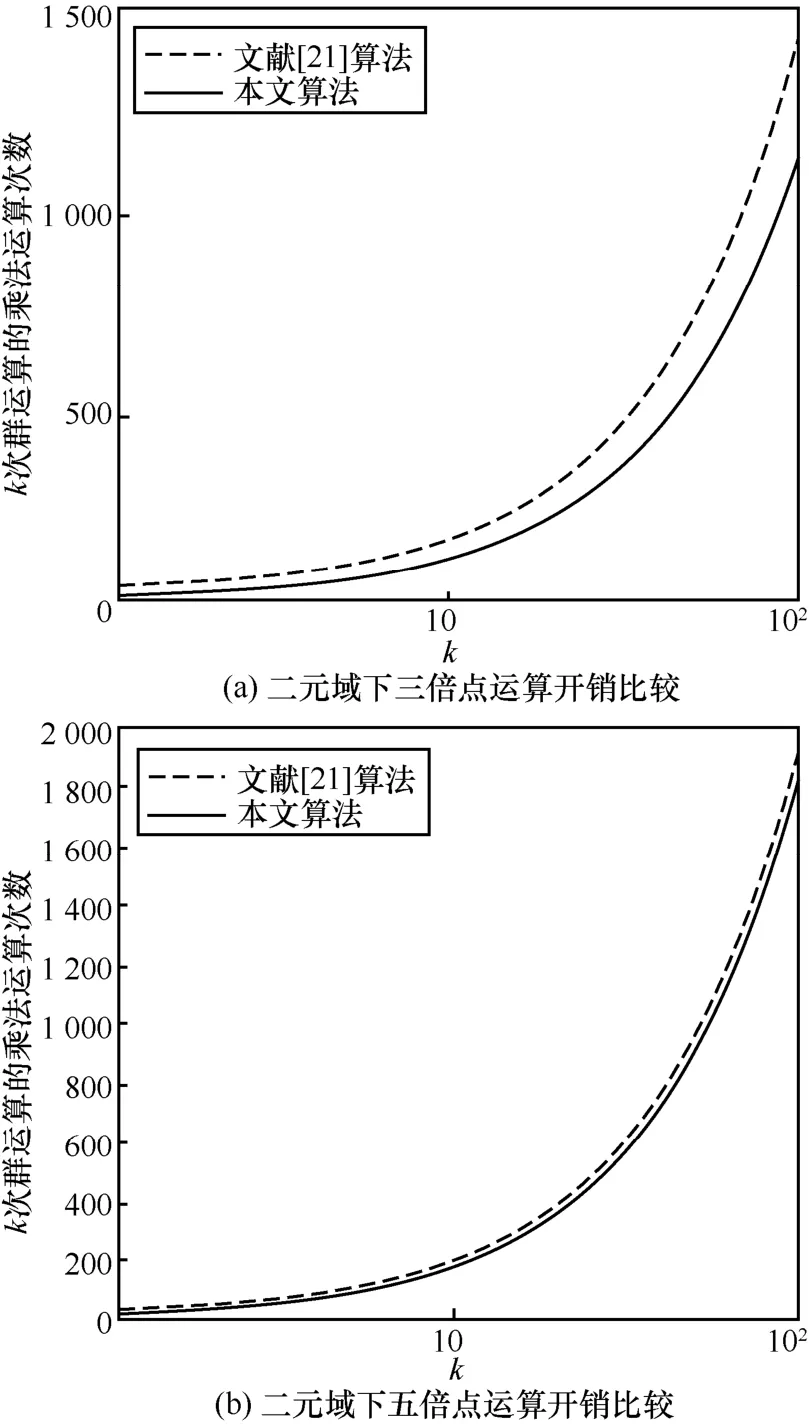
图4 二元域群运算开销比较

5.2 系统总开销分析

通过对椭圆曲线密码系统层次结构的分析，本文优化了群运算层和标量乘运算层，实现了系统整体效率的提升。表3就本文算法的系统总开销（换算为乘法运算次数）与对照算法的系统总开销进行了对比。由于本文所提的伪四维投射坐标向下兼容雅可比坐标（将aZ4舍去即可），可以计算出本文算法中一次点加运算的开销为7M+4S。此外，为了让对比更为公正客观，所有算法均未使用任何预计算。

表3 系统总开销比较

由表3可知，当密钥长度为160位时，本文算法的总开销比文献[14]降低了 57.79%，比文献[13]降低了36.09%，比文献[17]降低了26.82%，比文献[16]降低了23.32%，比文献[15]降低了12.94%，比文献[18]降低了8.70%。此外，文献[18]的算法只能运用于二元域，其余算法既可以运用于二元域，也可以运用于素数域。

5.3 能量分析攻击实验

5.3.1 实验环境搭建

本实验采用NewAE公司的Chipwhisperer-Lite实验平台[25]。该实验平台由2个部分组成：一部分为XMEGA开发板，供开发者编程；另一部分为采样器，可以采样开发板运行时的能量消耗波形。通过该实验工具能清楚分析出算法遭受能量分析攻击的情况。图5为Chipwhisperer-Lite实验平台的体系结构示意。5.3.2 抵御SPA攻击

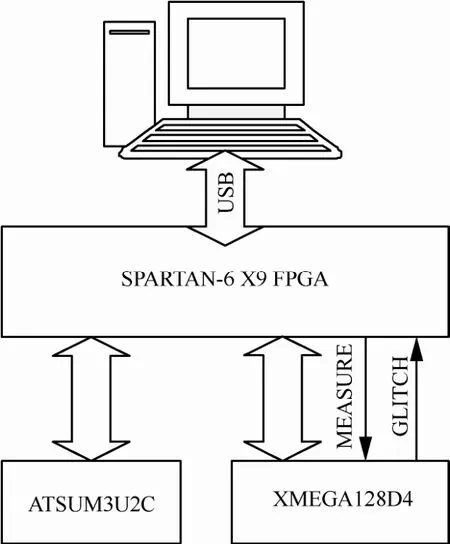
图5 Chipwhisperer-Lite实验平台的体系结构示意

由于不同的操作，处理器在不同时序上的能量消耗会体现出差异性。攻击者通过观察设备在进行加密运算的能量功耗曲线，对能量功耗曲线进行直观分析，找到能量功耗与操作的关系，达到获取密钥的目的。从算法4可以看出，标量乘运算每一次大循环都会经过连续五倍点运算、连续三倍点运算，再连续倍点运算，然后经过点加及相关其他域操作进入下一次大循环。为了检测算法4是否可以抵御SPA攻击，本文首先输入160位的私钥为

根据式(8)的输入，在标量乘运算的过程中，采样器会采集运算时的能量消耗曲线。图6描绘了采用平衡能量法前后能量波形对比。由于Chipwhisperer-Lite采样范围为26 000个时钟周期，本文截取第一次循环结束至第二次循环开始的能量波形，如图6(a)所示。其中，左边虚线框为倍点操作，中间点线框为点加及相关域操作，右边实线框为五倍点操作。

图6 采用平衡能量法前后能量波形对比

从图6(a)可以看出，相同的域操作虽然会由于操作数不同及噪声干扰，其振幅会有少许区别，但高低电位基本以周期的形式出现，从虚线框和实线框部分很容易看出倍点和五倍点操作的界限。将图6(a)中点线框部分放大得到图6(b)，由于在算法4中si∈ {1,− 1}，所以当sk=−1时，则会进行一次求逆运算。由于求逆操作开销极小（此处的求逆为2.2.2节中的群运算求逆，不是2.2.1节中开销极大的域运算求逆），几乎可以忽略不计，在图6(b)中也不明显。再将图6(b)放大得到图6(c)，图 6(c)中实线框标出的波形即一次求逆操作。而根据算法 3，上述k得到的sk=1，并不需要求逆运算。所以如果没有采用平衡能量法，其波形如图6(d)所示，攻击者即可通过波形差异获得si的取值。而使用平衡能量法，则每一次点加之前都会出现一次求逆操作，使攻击者无法通过能量波形获取si的取值，即无法从能量曲线直观地获取私钥信息。

5.3.3 抵御DPA攻击

DPA攻击的原理与SPA攻击的原理类似，不同的是它采用大量样本经过纠错技术和统计方法，通过样本之间的细微差别获取密钥信息。与SPA不同的是，DPA攻击并不需要了解密码系统实现的具体细节，并且对信噪比的要求比 SPA低。所以 DPA是目前能量分析攻击中最强大的一种。抵御差分能量分析攻击旨在利用随机策略，使攻击者无法通过多次运行获得统计数据。

本文采用Masking方法抵御DPA攻击。采用Masking方法与未采用Masking方法的能量波形对比如图7所示。

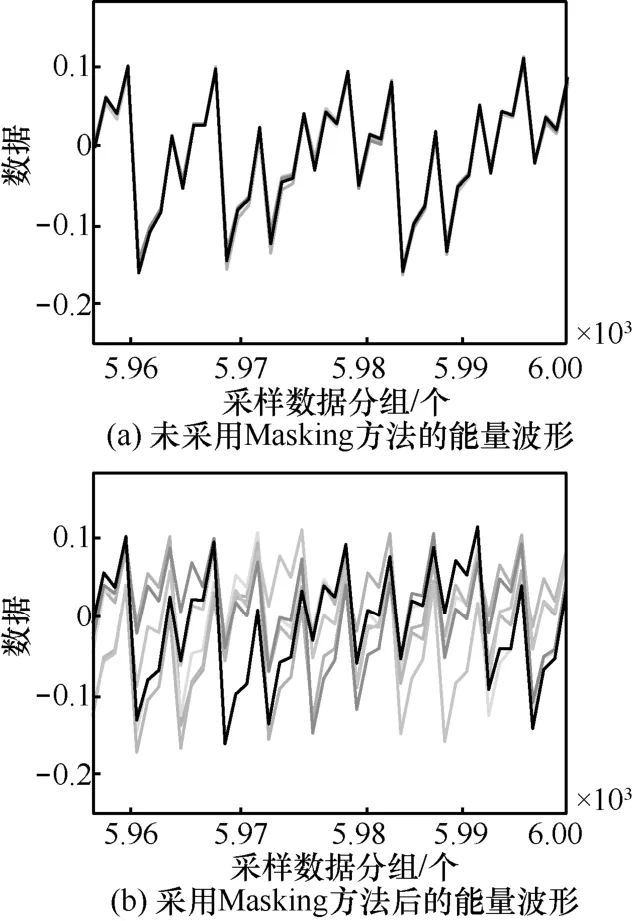
图7 采用Masking方法前后能量波形对比

图 7(a)描绘了未采用Masking方法的多次运行能量波形。可以看出，每一次运行的波形差别微乎其微，曲线重合度很高，给DPA攻击提供了条件。采用 Masking方法之后，其多次运行的能量波形如图 7(b)所示。由于每次标量乘运算之前基点都加上了一个随机点，其能量波形无论在幅度和相位上都有差异，攻击者无法通过DPA攻击来获取密钥信息。

6 结束语

本文建立了基于伪四维投射坐标的快速群运算并推导出基于伪四维投射坐标的多基链标量乘法，在群运算层和标量乘运算层对椭圆曲线密码系统进行了优化。为了对多基链生成算法进行优化，建立了基于拉格朗日乘数法的贪心策略，提出最短链存在定理并推导出最短链表。能量分析攻击实验表明，本文提出的分层优化策略可以有效地提高椭圆曲线密码系统的整体性能，并可抵御常见的能量分析攻击。

[1] RIVEST R, SHAMIR A, ADLEMAN L. A method for obtaining digital signatures and public-key cryptosystems[J]. Communications of the ACM, 1983, 26(1)∶ 96-99.

[2] KOBLITZ N. Elliptic curve cryptosystems[J]. Mathematics of Computation, 1987, 48(48)∶ 203-209.

[3] MILLER V. Use of elliptic curves in cryptography[J]. Lecture Notes in Computer Science, 1985, 218(1)∶ 417-426.

[4] SAQIB N. Key exchange protocol for WSN resilient against man in the middle attack[C]//IEEE International Conference on Advances in Computer Applications. 2017∶ 265-269.

[5] YEH H L, CHEN T H, SHIH W K. Robust smart card secured authentication scheme on SIP using elliptic curve cryptography[J]. Computer Standards &Interfaces, 2014, 36(2)∶ 397-402.

[6] SHENTU Q C, YU J P. A blind-mixing scheme for bitcoin based on an elliptic curve cryptography blind digital signature algorithm[J]. Computer Science, 2015∶ 1-17.

[7] GUERON S, KRASNOV V. Fast prime field elliptic-curve cryptography with 256-bit primes[J]. Journal of Cryptographic Engineering,2015, 5(2)∶ 141-151.

[8] IZU T, TAKAGI T. Exceptional procedure attack on elliptic curve cryptosystems[C]//International Workshop on Public Key Cryptography-pkc.2003∶ 224-239.

[9] MATHER L, OSWALD E. Pinpointing side-channel information leaks in Web applications[J]. Journal of Cryptographic Engineering, 2012,2(3)∶ 161-177.

[10] KOCHER P. Timing attacks on implementations of Diffie-Hellman,RSA, DSS, and other system[C]//International Cryptology Conference on Advances in Cryptology.1996∶ 104-113.

[11] MESSERGES T. Using second-order power analysis to attack DPA resistant software[J]. Springer Berlin Heidelberg, 2000, 1965∶238-251.

[12] 王敏, 吴震. 抗SPA攻击的椭圆曲线NAF标量乘实现算法[J]. 通信学报, 2012, 33(S1)∶ 228-232.WANG M, WU Z. Algorithm of NAF scalar multiplication on ECC against SPA[J]. Journal on Communications, 2012, 33(S1)∶ 228-232.

[13] MAMIYA H, MIYAJI A, MORIMOTO H. Efficient countermeasures against RPA, DPA, and SPA[J]. Springer Berlin Heidelberg, 2014,3156∶ 343-356.

[14] MISHRA P, DIMITROV V. Efficient quintuple formulas for elliptic curves and efficient scalar multiplication using multibase number representation[C]//International Conference on Information Security.2007∶390-406.

[15] DANGER J, GUILLEY S, HOOGVORST P, et al. Improving the big mac attack on elliptic curve cryptography[J]. Springer Berlin Heidelberg, 2016∶ 374-386.

[16] LI L, LI S. High-performance pipelined architecture of elliptic curve scalar multiplication over GF(2m)[J]. IEEE Transactions on Very Large Scale Integration Systems, 2016, 24(4)∶ 1223-1232.

[17] DUBEUF J, HELY D, BEROULLE V. ECDSA passive attacks, leakage sources, and common design mistakes[J]. ACM Transactions on Design Automation of Electronic Systems, 2016, 21(2)∶ 1-24.

[18] LIU Z, HUANG X, HU Z, et al. On emerging family of elliptic curves to secure Internet of Things∶ ECC comes of age[J]. IEEE Transactions on Dependable & Secure Computing, 2017, 14(3)∶ 237-248.

[19] MELONI N, HASAN M. Efficient double bases for scalar multiplication[J]. IEEE Transactions on Computers, 2015, 64 (8)∶ 2204-2212.

[20] CHO S, GWAL S, CHANG H K, et al. Faster elliptic curve arithmetic for triple-base chain by reordering sequences of field operations[J].Multimedia Tools &Applications, 2016∶ 1-13.

[21] PUROHIT G, RAWAT A. Elliptic curve point multiplication using MBNR and point halving[J]. International Journal of Advanced Networking & Applications, 2012∶ 1329-1337.

[22] PAAR C, PELZL J. Understanding cryptography[J]. Springer Berlin Heidelberg, 2010∶ 519-551.

[23] HASAN AE, REYHANIMASOLEH A. New regular radix-8 scheme for elliptic curve scalar multiplication without pre-computation[J].IEEE Transactions on Computers, 2013, 64(2)∶ 438-451.

[24] BERNSTEIN D, CHUENGSATIANSUP C, LANGE T. Double-base scalar multiplication revisited[R]. IACR Cryptology ePrint Archive,2017∶ 1-38.

[25] O’FLYNN C, CHEN Z. ChipWhisperer∶ an open-source platform for hardware embedded security research[C]// International Workshop on Constructive Side-Channel Analysis and Secure Design. 2014∶243-260.