基于不确定理论的能量收集可靠性建模及规划

王哲，李陶深，叶进，葛志辉，吴敏

（1. 广西大学电气工程学院，广西 南宁 530004；2. 广西大学计算机与电子信息学院，广西 南宁 530004；3. 广西电网有限责任公司，广西 南宁 530023）

1 引言

能量收集网络是一种新型的计算机网络形式，它融合了新能源技术的优势，通过搜寻各类环境能源，将其转化成可用的电能，从而作为主要或辅助的电源方式供给电子设备进行网络通信，完成某些特殊任务[1,2]，可以为网络设备的节能减排、植入型医疗设备、穿戴式设备、环境监测等提供新型的网络解决方案。

目前，该领域的相关研究成果主要集中在能量收集网络信道容量、离线/在线能量管理策略、能量与信息联合传输这3个方面。在基于信息论的能量收集网络研究方面，Ozel等[3]分别对配备无限容量电池、有限容量电池[4]以及无电池[5]的情况做了分析研究并得出相应结论及实现方法。离线能量管理策略的制订分为单用户通道和多用户通道。文献[6]提出一种多中继选择方案，根据当前时隙中继节点的能量收集状况，使用马尔可夫链（MC, Markov chain）模拟节点电池充放电过程，继而解决中继节点操作问题。文献[7]针对认知能量收集网络，提出一种系统吞吐量最大化的功率分配算法，在满足次用户节点能量因果性约束和主用户干扰限制的前提下，将节点的功率和能量协作联合优化问题解耦为分离的功率分配问题和逐个时隙的协作能量问题求解。在线能量管理策略主要使用马尔可夫决策过程（MDP, Markov decision process），根据是否能够获取完美的电量数据[8]、单/多用户[9]、电池损耗特性[10]、不同的感知/传输特性[11]等实际情景，分别建立相应的模型并求取最优解。

分析现有的研究成果可以看出，与传统网络相比，能量收集网络的难点在于有限能量的合理规划和使用，如何对能量收集网络的可靠性做出评估并实现网络的可靠运行成为新的挑战。目前，使用较为广泛的可靠性模拟方法有可靠性框图（RBD,reliability block diagram）、故障树（FT, fault tree）、马尔可夫链及形式化方法。文献[12]研究了网络服务系统中使用 RBD预测系统性能减弱退化效应所需的可靠性等级，包括不可靠数据传输、服务不可用、应用组件依赖和数据吞吐量异常等。文献[13]使用 RBD研究了通信协议的可靠性，提出节点和系统之间能够高效可靠通信的一系列规则；提出使用 RBD评价新协议的方法，例如，如能量高效聚类可靠性协议（REECP）和WSN的路由协议。文献[14]指出在通信控制系统（CCS, communication control system）中，可用基于FT的模糊逻辑表征运行状态随时间变化所引入的随机和不确定故障，从而分析并优化系统可靠性。文献[15]基于固有的双向推理技术，利用贝叶斯网络，简化大型智能电站需求分析FT模型，识别模型中的薄弱环节，继而提高底层通信网络的可靠性。文献[16]提出一种开源的概率模型检测器——PRISM，为系统构建并分析多类型概率模型提供支持。文献[17]提出了完整的基于Petri网的可靠性分析的网络架构。文献[18]提出了FT门的高阶逻辑形式化，使用完整的高阶逻辑定理证明作为核心进行FT分析。然而，上述工作尚未应用于能量收集网络的形式化可靠性分析中，且对能量收集网络中元件不确定性、网络动态特性、能量约束性的模拟尚未实现。

由于能量收集网络的可靠性应包含能量收集可靠性、数据感知可靠性和数据传输可靠性，因此，上述工作并不能直接应用于能量收集网络。文献[19]基于MDP，考虑能量收集传感器网络的数据感知与传输联合优化特性，建立可靠性模型，进而实现低复杂度的网络控制策略。文献[20]以电池耗尽概率和分组丢失率建立节点能量收集可靠性模型，提出在有限容量电池和有限容量数据堆栈情景下，实现可靠程度最大化的能量管理策略。文献[21]针对数据传输可靠性，设定可充电电池容量，假设在时隙开始时刻有数据分组到达且在下一时隙内没有传输即分组丢失的条件下，提出一种理论学习方法以最大化期望传输的总数据量。同时，作为能量收集网络运行的首要步骤，能量收集对能量收集过程的可靠性及收集量的评估直接影响了系统运行策略的制定和系统运行可靠性。文献[22]为能量收集过程建立了二阶马尔可夫链模型，并使用线性规划算法求解，但模型建立过程含有能量获取概率、能量消耗概率、数据产生概率和数据发送概率这4个参数，而文中假设这4个参数服从伯努利分布，并不合理。文献[23]使用排队论模型G/G/1/N和G/G/1/∞分别模拟有限容量电池和无限容量电池下的能量收集过程，并分别计算了节点的耗尽概率，但模型中的G/G部分需要已知概率分布，文中假设其以概率{0.3,0.3,0.2,0.2}取值于{1,2,3,4}，过于主观。同时，基于当前电池电量状态（SOC, state of charge）[4]的能量收集评估，由于电路元件的不确定性使其误差大于30%[24]。

与此同时，能量收集网络由于能量有限，难以采样足够的原始数据用以获得系统概率分布函数；而环境能量的诸多不确定性，也使先验知识的指导意义不大。因此，本文考虑能量收集环节能量是否到达以及能量收集量的多少等不确定情景，基于不确定理论，对可能发生的情景的置信程度给出评价，对网络节点能量收集的可靠性进行评估分析，提出基于模糊理论的节点可靠性建模方法，并分别建立节点无电池和配备无限容量电池情况下的可靠性模型；在此基础上，提出能量收集可靠性多层不确定规划模型，对模型求解，提出 EAA算法，并从理论上证明了算法竞争比的上界。最后，通过实际风功率数据的对比实验，验证本文所提方法在可靠性分析及系统优化中的可行性和有效性。

2 基于不确定理论的能量收集可靠性模型

环境能量的多样性与不确定性使收集功率难以预测，继而难以评估当前能量收集状态。本节使用模糊理论建立节点能量收集可靠性的数学模型，分别分析节点不配备电池和配备无限容量电池情况下的可靠性。电池均为可充电电池。

2.1 节点能量收集可靠性

考虑能量收集网络中节点配备能量收集装置，即通过收集周围环境能量（如风能、太阳能、电磁辐射等），将其转化为电能，供给节点完成数据传输。因此，能量收集网络可靠性的分析主要针对节点能量收集可靠性来展开，能量收集过程的不确定性和波动性均可能导致节点死亡。

定义 1 设定系统时间是连续分段且时段为单位长度，则节点在单位时段[t,t+1]内的能量收集可靠性Re(t,t+1)定义为节点在该时段内能够正常运行的程度，即

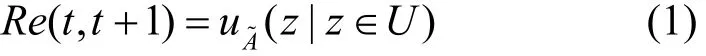
其中，U为论域，A为系统的特征函数，A~为特征函数的模糊集且为U的模糊子集。

2.2 无电池节点能量收集可靠性

考虑节点不配备电池的情况，即节点在当前时刻的运行状态依赖于当前能量收集状态，做如下假设。

假设 1 能量相对于数据进行了单位化处理，即一个单位的能量可以发送一个单位的数据。

假设 2 不考虑节点内部的时间成本，即当前收集的能量可以直接用于当前的数据发送。

假设 3 系统收集的能量全部用于数据发送，不考虑节点中如传感器采集及电路自身运算等能耗；换言之，数据的发送速率即节点的能量消耗速率。

在单一时段内，构建能量收集网络模糊排队论模型F/F/1，其中，能量消耗速率与能量收集速率分别用模糊集D~={(x,uD~(x))|x∈X}、C~= {(y,uC~(y))|y∈Y}表示。相应的隶属函数分别为uD~(x)、uC~(y)。这里，模型F/F/1中的数据发送速率即能量需求速率，也即传统排队论中的顾客到达速率；相应地，能量收集速率即服务速率。当数据发送任务到达而能量短缺时，数据分组则进入队列等待收集能量继续发送。此时，单位时段中数据分组发送等待概率即系统能量耗尽概率。

假设N(t)表示在t时刻系统中等待发送的数据分组数量，且令

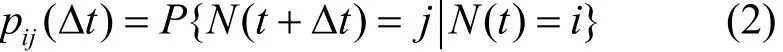
其中，pij(△t)表示t时刻等待发送的数据分组数量为i、t+△t时刻等待发送的数据分组数量为j的概率。于是，{N(t),t≥0}为{0,1,2,…}上的生灭过程。

定理 1 定义j=1,2,…。当ρ＜1以可信性1成立时，有{pj,j≥0}存在，且与数据分组队列的初始状态无关，其中，

定理1的证明如下。

令则有

于是，此生灭过程的绝对分布pj(t)=P{N(t)=j}，j≥0的福克—普朗克方程组，即满足如下方程组。

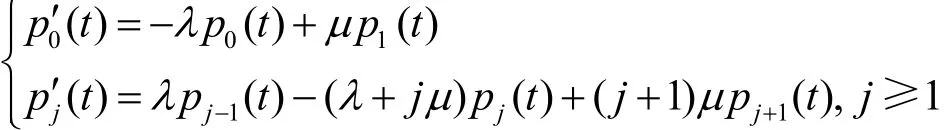
解之得

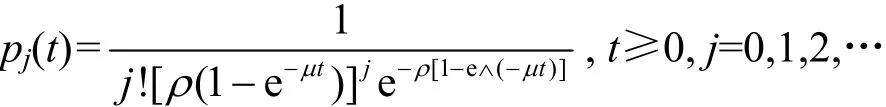
求极限得

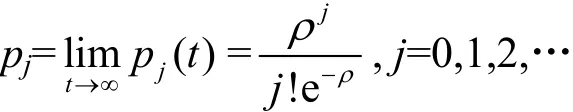
由于

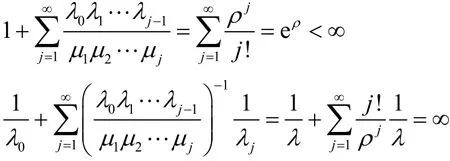
因此，平稳分布{pj,j≥0}存在，且与初始条件无关。证毕。

于是，节点正常运行的概率为

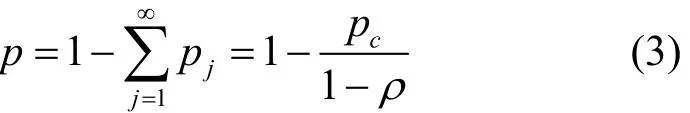
其中，

由于模糊排队论模型F/F/1中的能量消耗速率与能量收集速率均为模糊数，因此节点正常运行概率作为系统特征值，也是一个模糊数。根据 Zadeh扩展原理，的隶属函数为

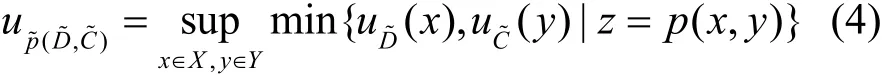
按照α-截集的定义，可以求出D(α)和C(α)的上下界，分别为[xαL,xαU]和[yαL,yαU]，其中，D(α)和C(α)分别为D~和C~的α-截集。设能量消耗速率与能量收集速率分别用梯形模糊变量[x1,x2,x3,x4]和[y1,y2,y3,y4]表示，其中，{x1,x2,x3,x4,y1,y2,y3,y4}≥0，则有

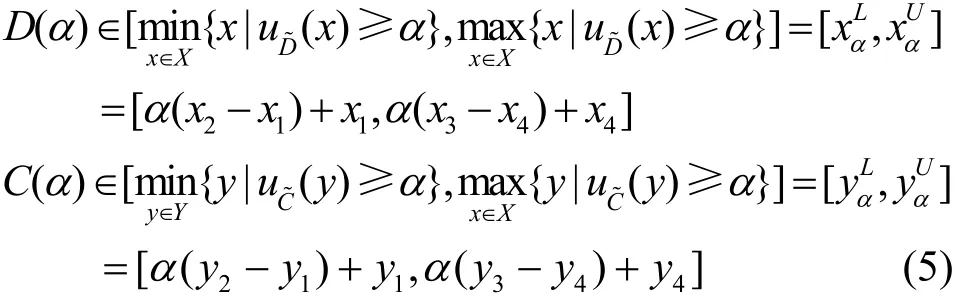
依据D(α)和C(α)的上下界，可求得的上下界[(p)αL, (p)αU]，分别对α求反函数，继而得到的隶属函数为

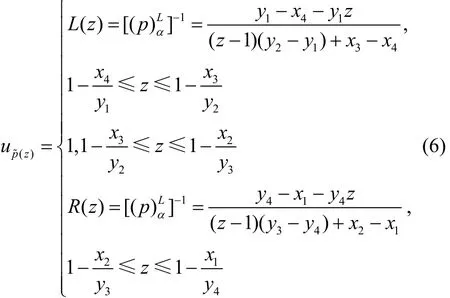
由此即可得到无电池情况下，网络节点在该时段内能量收集的可靠性。式(6)的物理意义在于：当节点耗尽概率趋于0时，其左边界和右边界即L(z)与R(z)均与量值{y1,y2,y3,y4}无关，节点可靠性仅与量值{x1,x2,x3,x4}有关，即与系统当前的能量收集状态无关；节点正常运行的可信性测度Cr{A}只与系统当前的数据发送速率有关。因此，基于节点可靠性所设计的节点运行规划，应依据节点当前能量收集状态，合理规划数据发送速率，从而实现节点的可靠运行。

2.3 无限容量电池节点能量收集可靠性

当节点配备较大容量的可充电电池且电池容量远大于节点能量收集装置的容量时，可认为节点配备无限容量电池。此时节点的运行状态依赖于电池中的剩余电量。类似于2.2节中的假设，且当前收集的能量在完成数据发送任务后将剩余能量存入电池。

此时，能量存储队列可模拟为F/F/1/∞队列。但应注意，不同于2.2节无电池情况，此时能量存储过程为传统排队论中顾客到达过程，能量存储队列的消耗过程为顾客服务过程。设能量存储队列的能量进入与离开速率分别为x、y，则剩余电量R(t)作为离散队列的长度，可用连续过程r(t)近似，该连续过程即单位时段△t内的电量增加量。

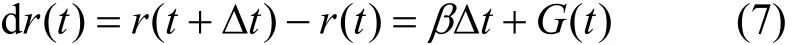
其中，β=x−y为漂移系数，G(t)为均值为0、方差为1的高斯白噪声。

给定电池的初始电量r(t=0)=r0，则通过求解r(t)的条件概率密度，就可得到模糊系统的特征值。能量存储队列在t时刻的条件概率密度函数为

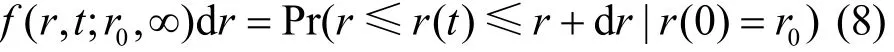
式(8)满足边界条件r(t)≥0下的前向扩散方程

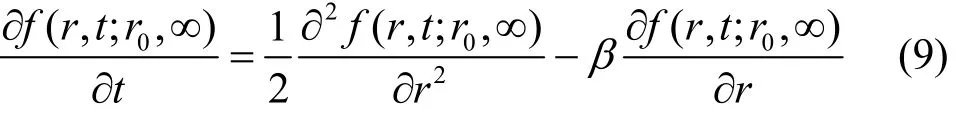
利用文献[25]中图论的方法，式(9)可以转化为

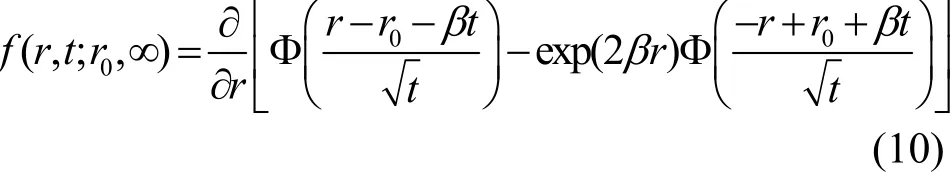
其中，Φ(·)为标准正态积分。

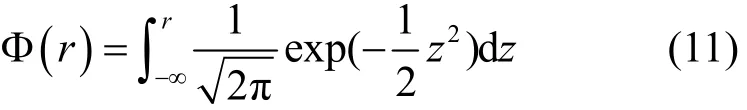
定义E(r0)为初始电量r0时的能量耗尽时长，则有

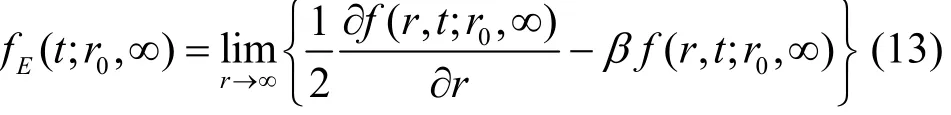
通过原点吸收壁的扩散方程，可以求得E的密度函数为求解式(13)的偏微分方程，得出E的条件概率密度函数为

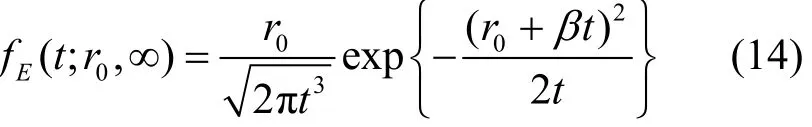
继而得出E的矩母函数为

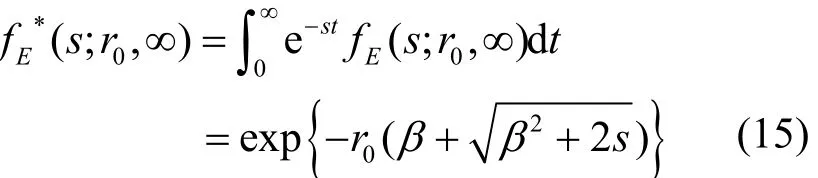
当s趋近于0时，式(14)从r0出发到达吸收壁的概率为Pr(0;r0,∞)。因此，节点正常运行的特征函数为

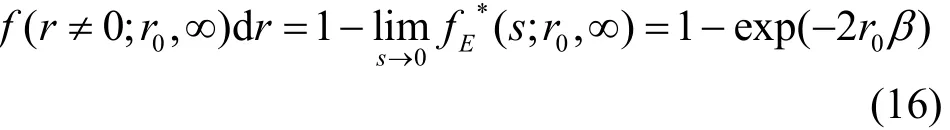
其中，exp(−2r0β)应是不大于1的实数，也即当β≥0时，节点正常运行的特征值是非 0的。类似于2.2节，设能量存储队列补充与消耗速率分别用梯形模糊变量={(x,uD~(x))|x∈X} =[x1,x2,x3,x4]和={(y,uC~(y))|y∈Y}=[y1,y2,y3,y4]表示，其中，{x1,x2,x3,x4,y1,y2,y3,y4}≥0，根据Zadeh扩展原理与α-截集的定义，可以求出D(α)和C(α)的上下界，分别为[xαL,xαU]和[yαL,yαU]，即

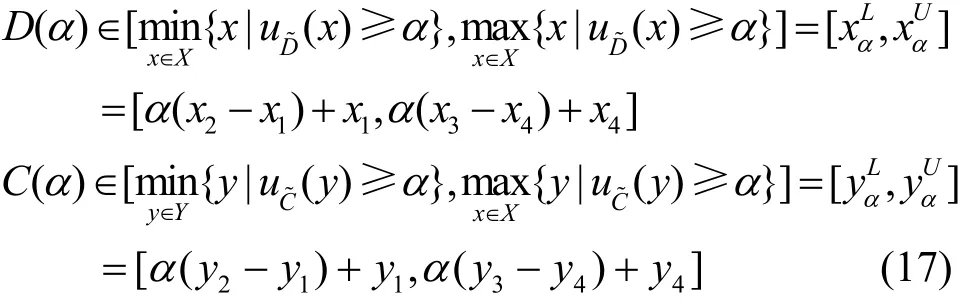
依据D(α)和C(α)的上下界，可求得特征函数的上下界[(f)αL,(f)αU]，分别对α求反函数，继而得到的隶属函数为

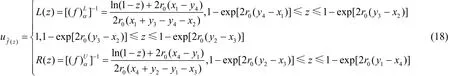
由此可得无限容量电池情况下，能量收集网络节点在当前时段内的能量收集可靠性。由式(18)可以看出，当特征函数趋于1时，节点可靠性与电池的初始电量r0无关。该结论也可以通过使用定理1中数据队列的证明方法得出。

3 基于能量收集可靠性的能量收集网络系统规划方法

基于第2节建立的能量收集可靠性模型，本节建立能量收集网络多层不确定规划模型，将其转化为等效清晰模型，提出满足能量收集可靠性前提下的系统规划方法。然后，提出基于不确定理论的能量平均分配算法（EAA），并从理论上证明算法竞争比上界。

3.1 竞争比

令P是依赖于请求变量序列σ={σi|i=1,2,3,…}的最优化问题。一个求解P的在线算法A，其请求序列为σ={σi|i=1,2,3,…}，且其服务于当前请求时对未来请求未知，则其目标函数为PA(σ)。一个求解P的最优离线算法O已知所有请求队列，其可实现最大目标函数PO(σ)。

定义2 令A是求解最优化问题P的任一在线算法。A是cA-竞争的或具有竞争比cA，当且仅当对于所有输入序列σ，有，则最优竞争比定义为

3.2 系统模型

考虑在源点与目标节点之间的无线通信信道，则t时刻目标的接收信号为

yt=Ptht xt+nt(19)

其中，xt为源点传输信号，Pt为源点传输功率，ht为衰减系数，nt为均值为0、方差为1的加性高斯白噪声信号且时间独立。假设衰减过程为黑箱模型[26]，即衰减系数ht在w个时段中连续且恒定。该w个时段组成一个时间间隔，间隔长度为w。因此，在第n个时段中，衰减系数可记作hn，n=1,2,3,…,N。假设源点使用环境能源供电，配备无限容量电池，且在第n个时段开始时电池剩余电量为En。

考虑任意能量收集过程的衰减信道，即时段n中对未来时段衰减系数和能量收集过程未知。假设在每个时段的起始，源点得知该时段内的衰减系数hn和剩余电量En。源点在时段n中利用衰减系数和能量的相关信息制定传输策略，实现其效益最大化。

本文考虑最大化源点可实现速率。假设源点在时段n中共用掉能量为BEn，同时由于能量有限性约束，即B≤1。则时段n中的可实现速率为

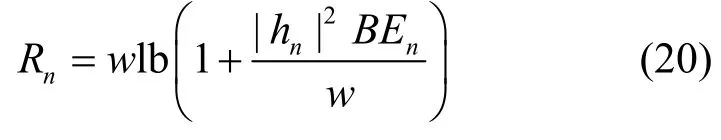
于是，N个时段中的累积速率为

由于能量收集过程是模糊的，最优化问题的价值函数R不能直接最大化，因此，考虑最大化其期望值。假设gi(x,y)为不确定约束，由于该约束未能定义清晰可行集，因此通常写成置信水平形式，αi为其置信水平。于是，最优化问题R可写为

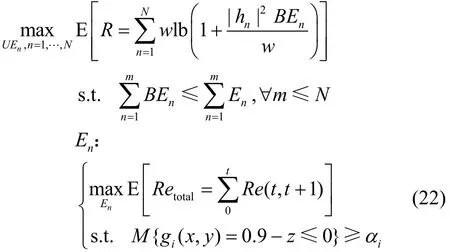
因此，寻找最优在线算法A*，实现最优竞争比为

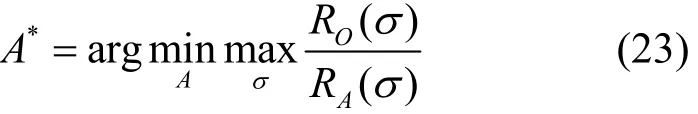
其中，σ=((|h1|2,E1),(|h2|2,E2),…,(|hN|2,EN))为N个时段中衰减系数即能量收集值。则最优竞争比为

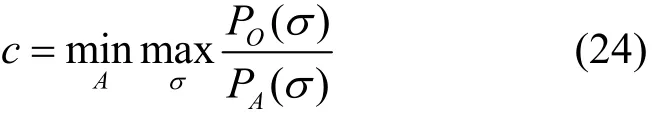
对于式(22)表述的最优化问题，文献[27]给出了最优离线算法，限于篇幅，这里不再介绍该算法。

3.3 等效清晰模型

由于式(22)表述的优化问题为多层不确定规划形式，无法直接求解，需转化为等效清晰模型。

令ξ1,ξ2,…,ξn为独立的不确定变量，具有不确定分布ψ1,ψ2,…,ψn。不失一般性，假设f为一实函数，且随ξ1,ξ2,…,ξk单调上升，随ξk+1,ξk+2,…,ξn单调下降，则不确定目标函数的期望值形式可转化为

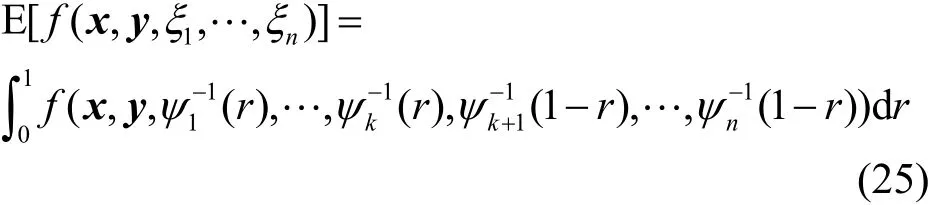
其中，x、y为决策向量。

假设g为一实函数，且随ξ1,ξ2,…,ξk单调上升，随ξk+1,ξk+2,…,ξn单调下降，则不确定约束函数的置信水平M{g(x,y,ξ)≤0}≥α可转化为

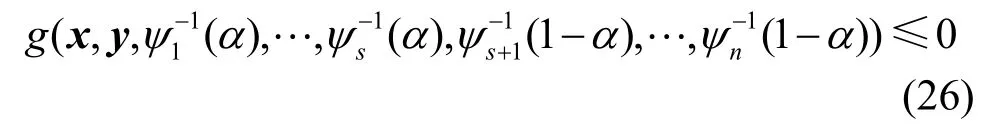
依据上述方法，式(22)的优化问题的等效清晰模型为

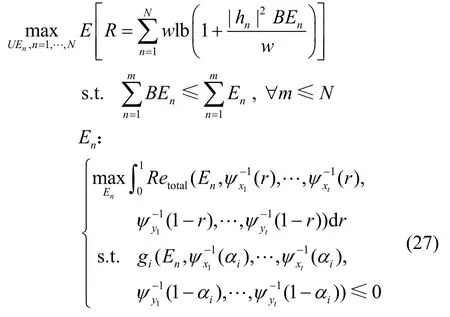
可见，为了求解式(22)的不确定规划问题，需要找到合适的数值方法求解其等效清晰模型。目前，求解多层规划模型的方法有极值点算法、k-th最优算法、分支界定算法、下降法以及遗传算法等。本文采用遗传算法求解该问题，求解过程采用了文献[28]给出的Nash均衡和Stackelberg-Nash均衡的求解方法。算法的具体步骤如下。

Step1 定义参数：种群规模、交叉概率、变异概率。

Step2 从可行域中随机初始化染色体。

Step3 通过交叉和变异，更新染色体。

Step4 对于每个染色体，利用遗传算法求解第二层规划问题的Nash均衡解。

Step5 依据Stackelberg-Nash均衡求解头层规划目标函数值。

Step6 计算每个染色体对应的适应度函数值。

Step7 使用轮盘赌选择（roulette wheel selection）算法选择新的染色体。

Step8 给定循环上限，重复Step3～Step7。

Step9 输出最优染色体即为最优解。

由于遗传算法受到实际应用中系统资源与时限的约束，仅以一定概率趋于最优解，因此，3.4节给出最优在线算法与竞争比上界，并证明该算法求出的解为最优解。

3.4 竞争比上界

基于不确定规划的能量收集可靠性模型，为了确保节点运行可靠性，使用在线算法不需要对未来能量收集状态进行预测；而使用遗传算法等优化算法，会占用过多的节点资源，增加处理器的能耗和时延。为此，本文设计了一种基于不确定理论的能量平均分配算法。使用 EAA算法，如果在时段n中电池可用电量为En*，则在剩余时段中算法将均匀分配当前可用能量，即在新的能量到达之前，每个时段消耗能量为，如图1所示。由图1可知，EAA算法是在线算法且并不依赖未来时段信息，同时也满足能量有限性约束。

定理2 EAA算法求解式(22)的优化问题是N-竞争的。同时，EAA是最优算法。

证明过程如下。

证明 在式(22)的优化问题中考虑松弛二级优化目标，即假设一级优化目标具有任意输入序列σ=((|h1|2,E1),(|h2|2,E2),…,(|hN|2,EN))。考虑时间间隔n且En≠0，记作k1,…,kp，其中，p≤N。不失一般性，假设k1=1，即时段1中可用能量非0。该假设是合理的，否则，可以从第k1时间间隔开始并移除前（N−k1−1）个时间间隔。令i表示介于时间间隔ki+1和ki之间的时段。第p个时间间隔表明kp间的时段数量，即该时间间隔结束时有新能量到达，且最后时段为N。为了便于阐述，令第i个时段中输入序 列 为

令为时段i=1,…,p中衰减系数的最大值，即。那么，第i个时段的输入序列可增强为

可见，的可实现速率优于σ，因此RO(σ)。由于能量有限性约束，在任意时间间隔i中，可消耗的最大能量为。因此，任意时间间隔i中的最大可实现速率可通过消耗时间间隔i之前的全部能量来实现。

进一步地，由可得，每一个时间间隔中的衰减系数均已知，因此任意时间间隔中最优离线算法的能量消耗在该时间间隔中的每一时段中是相等的，因此有

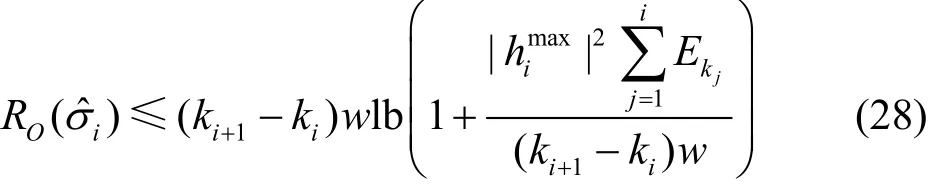
其中，(ki+1−ki)w是第i个时间间隔的长度。为了获得上界，需要对能量约束进行松弛，允许在时间间隔1中消耗E1的能量，在时间间隔2中消耗E1+E2的能量，然后时间间隔p中消耗的能量为如图1所示。于是有

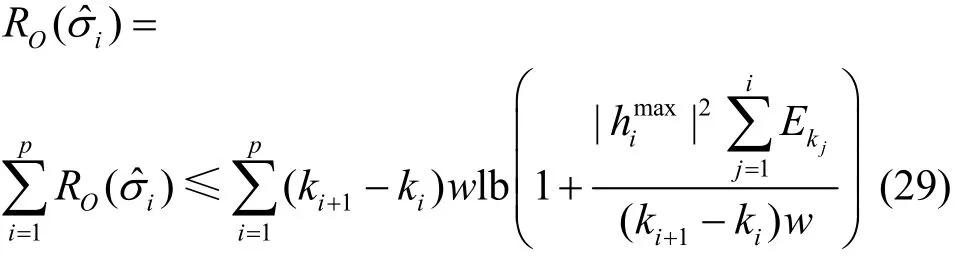
式(29)可视为的上界，EAA算法的竞争比上界。

下面，分析 EAA算法的速率的下界。考虑原始输入序列σ，使用EAA算法，令时间间隔i中任意时段n的消耗能量为BEni。那么，，且。简单的代数转化可得。于是，使用EAA算法，对于每一个时间间隔i=1,2,…,p，仅考虑在σi中实现最大衰减系数|himax|2的一个时段为

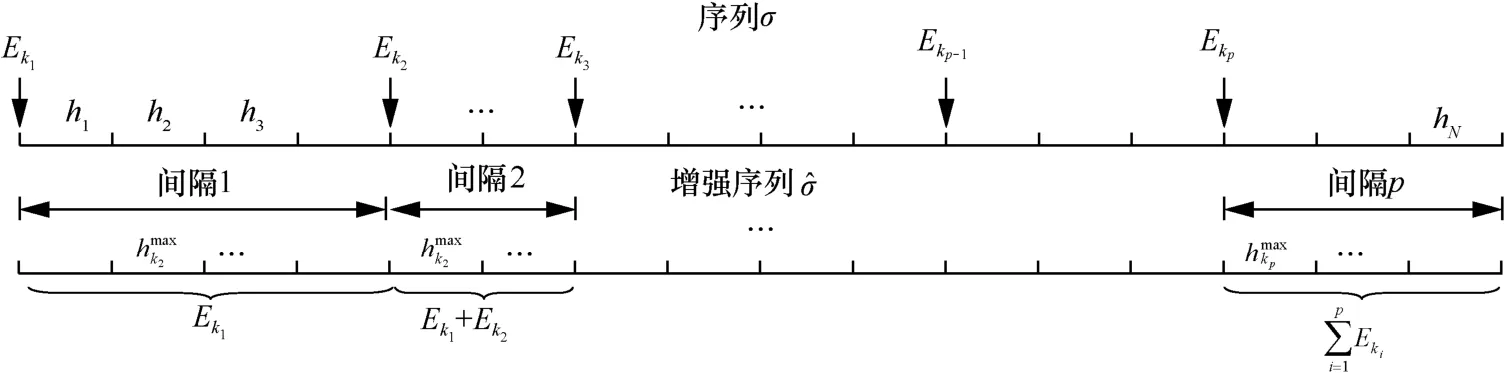
图1 EAA算法

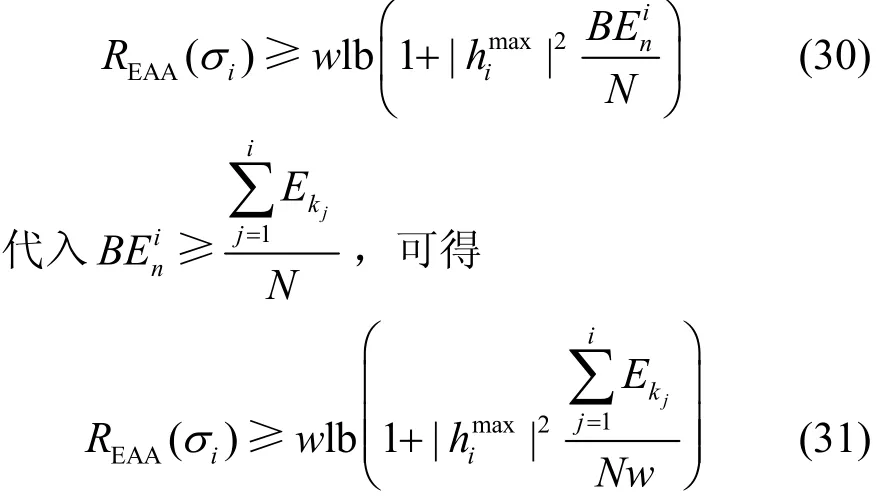
总的可实现速率为

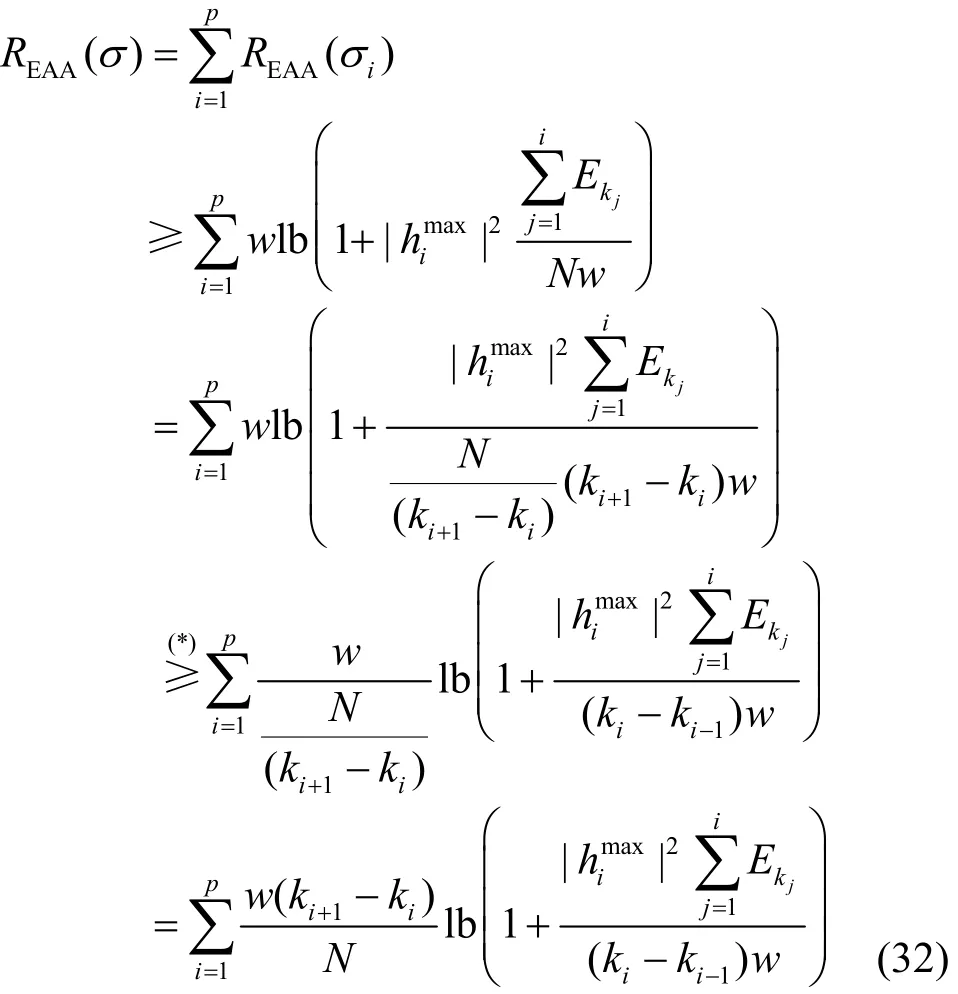
其中，(*)是基于推导出来的，x,y≥1。因此，通过式(29)和式(31)可得，EAA算法的竞争比为

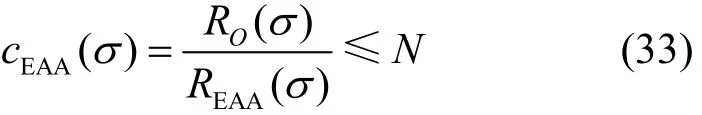
由此，依据前文竞争比定义可得，EAA算法求解式(22)的优化问题是N-竞争的；使用EAA算法所得的上界值，即系统所能实现的最大可实现速率，继而EAA算法为求解优化问题式(22)的最优算法。

4 仿真分析

以实际的风电数据为例，通过可靠性验证、遗传算法求解问题的效率、竞争比这3个仿真实验，说明本文所提能量收集可靠性模型及基于不确定理论的能量平均分配算法（EAA）的可行性和有效性。

4.1 实验数据准备

由于风能较太阳能在数据上而言具有更大的不确定性，作为模型的输入更能测试模型的顽健性。因此，在验证仿真实验中模型的输入数据采用了国内某电网公司2017年4月1日～30日共30天的风功率实际值，数据采样间隔为15 min，故日内时段为96个。为了保证能量收集与能量消耗环节数据的匹配性，风电数据与系统能耗数据均相对于自身的装机容量进行了标幺化处理（采用标幺单位制，单位为pu），即最大值均为单位量值；同时在时间尺度上，仿真实验遵循原数据的序列特性并假设具体的时隙长度由系统处理频率决定。仿真实验中数据的特征如图2所示，风功率收集速率在0至满额装机容量之间均有数据分布且日间数据差异较大；负载能耗需求则呈现一定的日内及日间规律性。

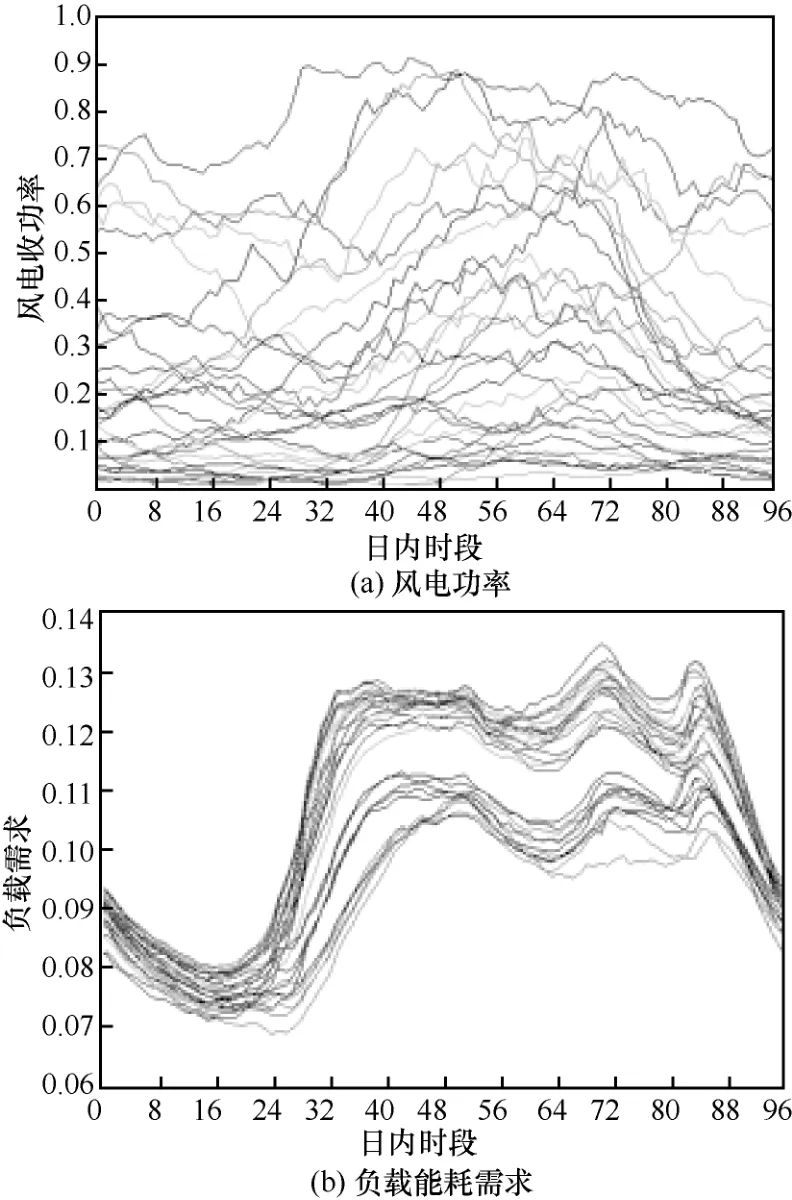
图2 仿真实验中数据的特征

4.2 可靠性验证

可靠性验证和对比分析主要是对以下4种方法进行的：1) 无能量规划，即当前时段所收集的能量仅用于当前时段的数据任务；2) 文献[29]中基于场景生成的能量规划方法，其中节点配备无限容量电池，生成日风电功率序列个数为 500，单时段内功率计划值为其平均值；3) 基于本文可靠性最大化的能量规划方法，其中置信水平为0.95，节点配备无限容量电池；4) 文献[23]中基于排队论G/G/1/∞的建模方法，优化节点的耗尽概率，评估每一时段的节点能量收集可靠性。

4种方法能够实现的节点能量收集可靠性的实验结果如图3所示，数据统计结果如表1所示。从表1可以看出，本文所提方法的可靠性为1的时段数量最多，且系统在2 880个连续时段内无0可靠性时段，即能够稳定运行。值得指出的是，文献[23]提出的基于排队论的方法的可靠性1时段数虽然少于文献[29]提出的基于场景生成的能量规划方法，但其可靠性曲线更为稳定，这是因为基于排队论的方法的模型是在保障节点最低耗尽概率的前提下计算得出的。

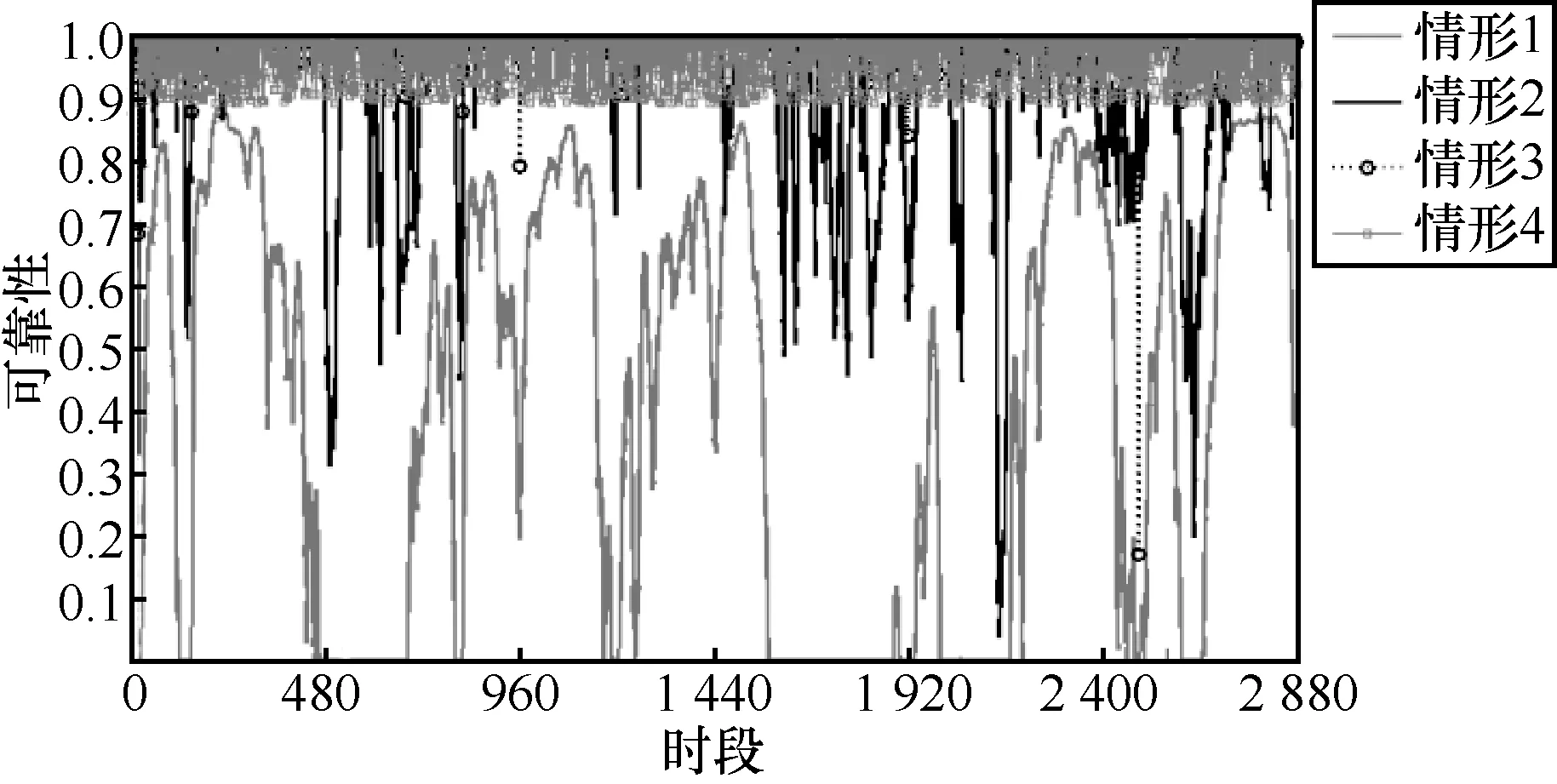
图3 4种方法能够实现的节点能量收集可靠性的实验结果

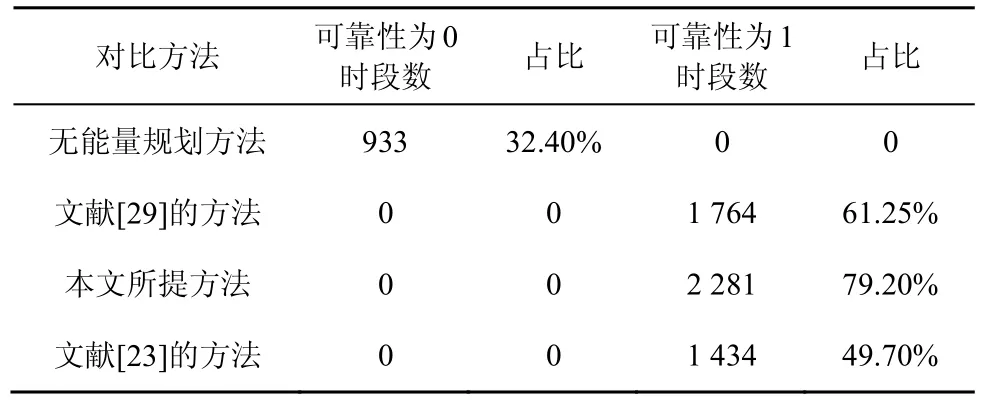
表1 数据统计结果

4.3 遗传算法求解

本节通过遗传算法求解等效清晰模型，以验证EAA算法在求解优化问题(22)时的顽健性。实验中分别设置了不同的种群规模、交叉概率、变异概率，算法最大的演化次数为 200。基于遗传算法求解式(22)表述的多层不确定规划问题的结果如表2所示。其中，Stackelberg-Nash均衡解并不唯一，表2中给出的目标函数值为6次实验结果。为了验证遗传算法求解该多层不确定规划问题的顽健性，算法使用了不同的种群规模、交叉概率和变异概率，从而得到 6次实验中目标函数的最大百分比误差为即EAA算法在求解该优化问题中，不同参数所求得的目标函数的最大百分比误差为 7.9%。该值越小，说明所述 EAA算法的顽健性越好。

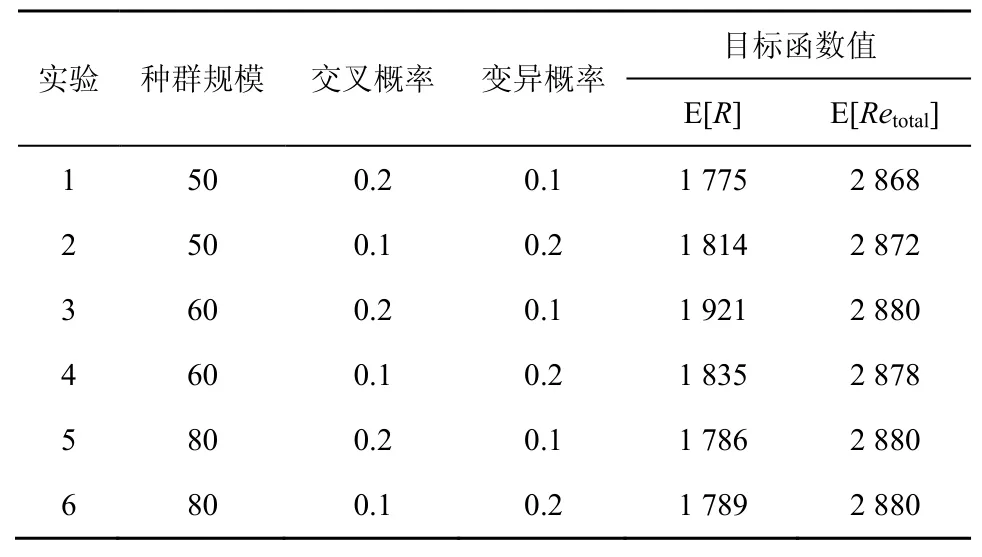
表2 遗传算法求解结果

4.4 竞争比

竞争比方面的仿真实验主要是验证本文所提能量平均分配算法（EAA）的性能。假设时间间隔长度为10个时段，即N=10。图4给出了基于历史数据的场景生成算法和基于模糊集的 EAA算法的竞争比柱状图。

从图4可以看出，本文所提EAA算法能够对目标函数值进行更有效的优化，同时由于系统资源有限，优化结果以一定的概率趋于最优，因此，图 4中部分数据竞争比大于 2。该结论也可通过文献[26]中针对AWGN信道、固定字节的最小化传输时间优化问题进行验证，当信道衰减系数退化为常量时，存在最优在线算法使竞争比小于 2。本文所提的基于不确定理论的规划方法不需要进行大量历史数据的训练，较场景生成方法更节省系统资源，同时能够实现更好的系统规划效果。

5 结束语

针对能量收集网络，本文提出了能量收集不确定环境下的可靠性模型。首先基于能量收集模糊集，定义网络节点能量收集可靠性，分别建立节点无电池和无限容量电池下的可靠性模型；进而提出基于可靠性的能量不确定多层规划模型，转化为等效清晰模型求解，然后提出基于不确定理论的EAA

算法，并在理论上证明了算法竞争比上界。仿真验证结果表明，基于不确定理论的能量收集网络方法能够有效评估分析节点能量收集可靠性，并实现更好的系统规划效果。

[1] ULUKUS S, YENER A, ERKIP E, et al. Energy harvesting wireless communications∶ a review of recent advances[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3)∶ 360-381.

[2] LU X, WANG P, NIYATO D, et al. Wireless networks with RF energy harvesting∶ a contemporary survey[J]. IEEE Communications Surveys& Tutorials, 2014, 17(2)∶ 757-789.

[3] OZEL O, ULUKUS S. Achieving AWGN capacity under stochastic energy harvesting[J]. IEEE Transactions on Information Theory, 2012,58(10)∶ 6471-6483.

[4] OZEL O, ULUKUS S. AWGN channel under time-varying amplitude constraints with causal information at the transmitter[C]//Asilomar Conference on Signals. 2011∶ 373-377.

[5] TUTUNCUOGLU K, OZEL O, YENER A, et al. Binary energy harvesting channel with finite energy storage[C]//IEEE International Symposium on Information Theory Proceedings. 2013∶ 1591-1595.

[6] 田贤忠, 郭敏, 何佳存, 等. 能量捕获协作中继网络多中继节点选择策略[J]. 通信学报, 2017, 38(Z2)∶ 1-7.TIAN X Z, GUO M, HE J C, et al. Multi relay node selection strategy for energy capture collaborative relay network[J]. Journal on Communications, 2017, 38(Z2)∶ 1-7.

[7] 谢振威, 朱琦. 基于能量协作的认知能量采集网络功率分配算法[J].通信学报, 2017, 38(9)∶ 176-184.XIE Z W, ZHU Q. Power allocation algorithm for cognitive radio energy harvesting networks based on energy cooperation [J]. Journal on Communications, 2017, 38(9)∶ 176-184.

[8] MICHELUSI N, STAMATIOU K, BADIA L, et al. Operation policies for energy harvesting devices with imperfect state-of-charge knowledge[C]//IEEE International Conference on Communications.2012, 11(18)∶ 5782-5787.

[9] TESTA D D, MICHELUSI N, ZORZI M. On optimal transmission policies for energy harvesting devices∶ the case of two users[C]//Tenth International Symposium on Wireless Communication Systems. 2013∶1-5.

[10] MICHELUSI N, BADIA L, CARLI R, et al. Energy management policies for harvesting-based wireless sensor devices with battery degradation[J]. IEEE Transactions on Communications, 2013, 61(12)∶4934-4947.

[11] JAGGI N, KAR K, KRISHNAMURTHY A. Rechargeable sensor activation under temporally correlated events[J]. Wireless Networks,2009, 15(5)∶ 619-635.

[12] XIN J, GUO L, HUANG N, et al. Network service reliability analysis model[C]//IEEE Conference on Prognostics and System Health Management. 2013∶ 511-516.

[13] DÂMASO A, ROSA N, MACIEL P. Reliability of wireless sensor networks[J]. Sensors, 2014, 14(9)∶ 15760-15785.

[14] PENG Z, MU X, YIN Z, et al. An approach of fault diagnosis for system based on fuzzy fault tree[C]//International Conference on Multimedia and Information Technology. 2008∶ 697-700.

[15] WANG Z, YAN X, GE W, et al. Analysis of network reliability on intelligent substation[C]//International Conference on Intelligent Networks and Intelligent Systems. 2014∶ 147-150.

[16] NORMAN G, PARKER D, ZOU X. Verification and control of partially observable probabilistic real-time systems[C]//International Conference on Formal Modeling and Analysis of Timed Systems.2015∶ 240-255.

[17] LIMA M A D Q V, MACIEL P R M, SILVA B, et al. Performability evaluation of emergency call center[J]. Performance Evaluation, 2014,80(C)∶ 27-42.

[18] AHMED W, HASAN O. Formal availability analysis using theorem proving[M]// Formal Methods and Software Engineering. Springer International Publishing, 2016∶ 226-242.

[19] KUANG Y, SHEN X S, YANG K, et al. Optimal reliability in energy harvesting industrial wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2016, 15(8)∶ 5399-5413.

[20] SRIVASTAVA R, KOKSAL C E. Basic performance limits and tradeoffs in energy-harvesting sensor nodes with finite data and energy storage[J]. IEEE/ACM Transactions on Networking, 2013, 21(4)∶1049-1062.

[21] BLASCO P, GUNDUZ D, DOHLER M. A learning theoretic approach to energy harvesting communication system optimization[J]. IEEE Transactions on Wireless Communications, 2013, 12(4)∶ 1872-1882.

[22] LIU J, DAI H, CHEN W. Delay optimal scheduling for energy harvesting based communications[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3)∶ 452-466.

[23] CAI L X, LIU Y, LUAN T H, et al. Sustainability analysis and resource management for wireless mesh networks with renewable ener-gy supplies[J]. IEEE Journal on Selected Areas in Communications,2014, 32(2)∶ 345-355.

[24] CHIASSON J, VAIRAMOHAN B. Estimating the state of charge of a battery[J]. IEEE Transactions on Control Systems Technology, 2005,4(3)∶ 465-470.

[25] KOBAYASHI H. Application of the diffusion approximation to queuing networks∶ part i equilibrium queue distributions[C]//ACM Sigme Symposium. 1973∶ 54-62.

[26] VAZE R. Competitive ratio analysis of online algorithms to minimize packet transmission time in energy harvesting communication system[C]//INFOCOM. 2013∶ 115-1123.

[27] JING Y, ULUKUS S. Optimal packet scheduling in an energy harvesting communication system[J]. IEEE Transactions on Communications, 2012, 60(1)∶ 220-230.

[28] LIU B. Stackelberg-Nash equilibrium for multilevel programming with multiple followers using genetic algorithms[J]. Computers &Mathematics with Applications, 1998, 36(7)∶ 79-89.

[29] 黎静华, 孙海顺, 文劲宇, 等. 生成风电功率时间序列场景的双向优化技术[J]. 中国电机工程学报, 2014, 34(16)∶ 2544-2551.LI J H, SUN H S, WEN J Y, et al. A two-dimensional optimal technology for constructing wind power time series scenarios[J]. Proceeding of the CSEE, 2014, 34(16)∶ 2544-2551.