ARX结构分组密码积分区分器的自动化搜索

韩亚，王明生

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2. 中国科学院大学网络空间安全学院，北京 100049）

1 引言

2015年，Todo[1]在欧密会首次提出积分可分性质，并利用该性质搜索分组密码积分区分器。同年，Todo[2]在美密会提出了分组密码算法MISTY1的6轮积分区分器，并对全轮MISTY1实施了理论的积分分析。根据可分性质积分传播规则，Todo给出10轮SIMON32的积分区分器，比实际搜索结果少了5轮。Wang等[3]提出了SIMON在原积分区分器的基础上增加一轮而不增加数据复杂度的方法。随后，Todo等[4]根据类 SIMON簇分组密码的结构特征，提出基于比特的可分性质，并搜索得到14轮SIMON32积分区分器。同时，他们通过改进基于比特的可分性质，提出利用三子集描述积分传播过程。利用三子集积分传播特征，他们搜索得到15轮SIMON32积分区分器。针对其他 SIMON簇分组密码算法[5]SIMON48/64/96/128，Todo等仅给出理论的积分区分器上界。

2016年，Xiang等[6]在亚密会上通过学习基于比特的可分性质，提出了一种基于混合线性规划（MILP, mixed integer linear programming）方法的积分区分器自动化搜索算法。该算法可用于搜索类SIMON簇及基于S盒的分组密码算法的积分区分器。针对 SIMON簇分组密码算法 SIMON32/48/64/96/128，他们分别给出了14、16、18、22和26轮积分区分器。但是他们无法给出与实际相符的15轮SIMON32积分区分器。随后，Sun等[7]通过改进Xiang等[6]的方法，提出搜索ARX结构分组密码积分区分器算法。基于比特可分性质，Sun等[7]通过建立积分传播模型并利用混合线性规划求解得到18轮HIGHT[8]积分区分器以及7轮LEA[9]积分区分器。同时，Sun等[7]还第一次给出了TEA[10]、XTEA、KATAN和KTANTAN等ARX结构分组密码算法的积分区分器。

针对一些小状态ARX结构分组密码，混合线性规划方法能有效地搜索积分区分器。但是对于大状态ARX结构分组密码算法如SPECK128，混合线性规划方法并不能给出有效的解决方案。通过学习基于比特的可分性质，利用三子集传播方程，本文提出一种基于SAT/SMT求解器自动化搜索ARX结构分组密码积分区分器的方法。SAT/SMT求解器可通过刻画比特向量可分性质，等价描述比特可分性质传播过程，并简化积分模型建立，加速模型求解过程。

2 比特可分性质传播模型

2.1 可分性质

积分可分性质由 Todo[1]首次提出并用于搜索分组密码积分区分器。集合空间的可分性质可通过点积运算描述。取输入变量，点积运算满足

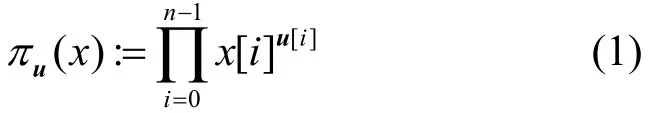
任意输入变量x= (x0,x1,… ,xm−1)，点积运算满足

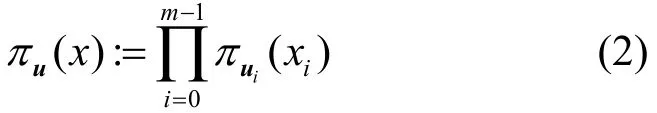
对于集合X，任意x∈X属于有限域空间，如果集合X满足可分性质，其中，k∈K为m维向量且第i个元素满足 0 ≤ki≤ni−1，对所有x∈X满足

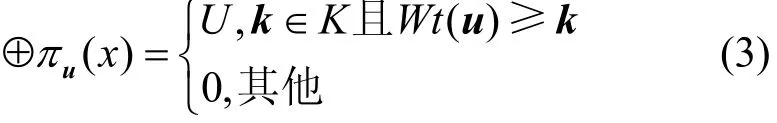
其中，U表示不确定取值，Wt(a)表示向量a的向量汉明重量，且Wt(a)=(wt(a0),wt(a1),… ,wt(am−1))。向量a、b的所有分量ai、bi均满足bi≤ai，则b≤a。

2.2 比特三子集积分可分性质

Todo等[4]将基于字的积分可分性质转换为比特状态，给出比特状态下的可分性质传播规则，并利用三子集更精确地描述积分可分性质的传播过程。

对于任意集合X，其元素属于(2)mF，如果集合X满足三子集积分可分性质，其中，k∈K为m维比特向量且第i个元素取值为 0或1，所有x∈X满足

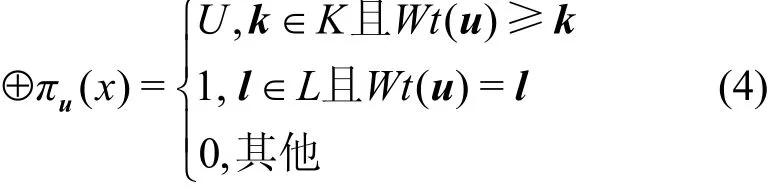
三子集积分可分性质比传统积分可分性质在传播过程中多了L集传播，能更加精确地描述积分可分性质的传播过程。

2.3 比特三子集传播规则

基于比特的积分可分性质，K集和L集在经过ARX结构分组密码轮函数中“分支”“异或”“与”操作时相互独立。

定义1F为分支操作，其输入 (x0,x1,… ,xm−1)∈(F2)m。任意比特xi,0 ≤i≤m−1经过分支操作F的K集传播kxi→(kyi,kzi)满足

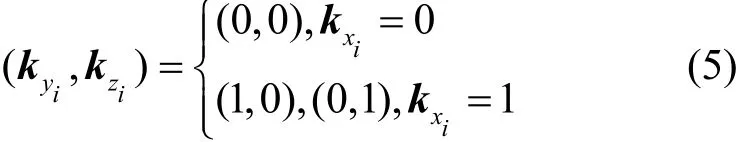
L集传播满足

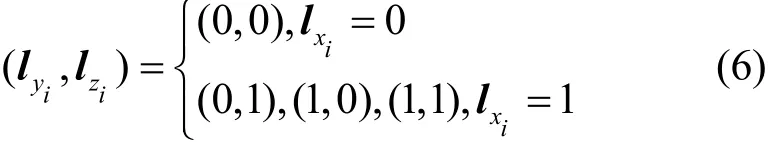
定义2F为异或操作，其输入 (x0,x1,…,xm−1)∈(F2)m。任意比特xi,xj,0 ≤i≠j≤m−1经过异或操作F的K集传播(kxi,kxj)→kyi满足

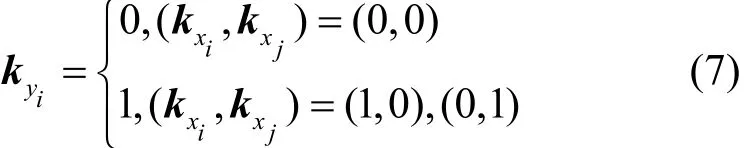
L集传播满足

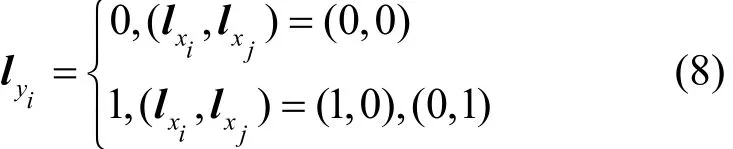
定义3F为与操作，其输入。任意比特经过与操作F的K集传播满足

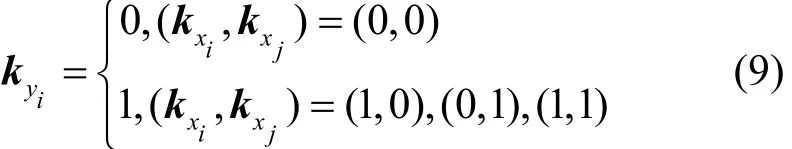
L集传播满足

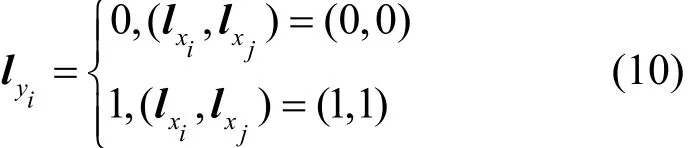
定义 4F为异或轮密钥操作，其输入(x0,任意L集向量经过异或轮密钥操作F后，如果满足lxi=0，需向K集中添加向量

例如，取m=4，异或轮密钥操作输入L集向量集合为((0,0,0,1),(1,0,0,0),(1,1,0,0))。其中，向量(0,0,0,1)经过异或轮密钥操作后K集增加3个额外向量((1,0,0,1),(0,1,0,1),(0,0,1,1))；(1,0,0,0)经过异或轮密钥操作后K集增加 3个额外向量((1,1,0,0),(1,0,1,0),(1,0,0,1))；(1,1,0,0)经过异或轮密钥操作后K集增加 2个额外向量((1,1,1,0),(1,1,0,1))，其中，(1,1,1,0)≥ (1,1,0,0)，(1,1,0,1)≥(1,1,0,0)被筛除。K集共增加 5个向量((1,0,0,1),(0,1,0,1),(0,0,1,1),(1,1,0,0),(1,0,1,0))。

定义5Fr为分组密码轮函数，假设初始三子集积分可分性质为。经过第i轮函数的输出，三子集积分可分性质满足，则r轮三子集积分可分性质传播路径表示为

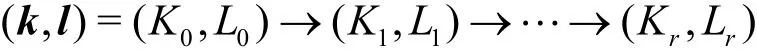
2.4 向量三子集传播规则

基于向量的积分可分性质，K集和L集在经过ARX结构分组密码轮函数“分支”“异或”“与”操作时相互独立。

定义 6 二分支操作输入。经过二分支操作的K集传播满足L集传播满足

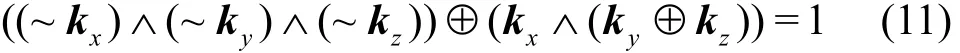
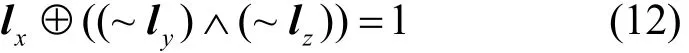
定义7 三分支操作，输入x=(x0,经过三分支操作的K集传播满足L集传播满足

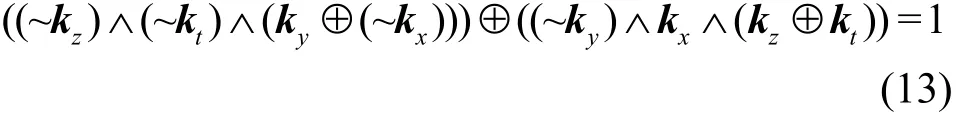
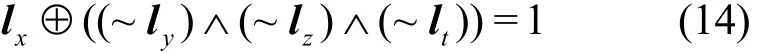
定义 8 二异或操作x⊕y=z，输入x=(x0,x1,… ,xm−1),y =(y0,y1,… ,ym−1)∈ (F2)m。经过二异或操作的K集传播 kp2xor((kx, ky) →kz)满足

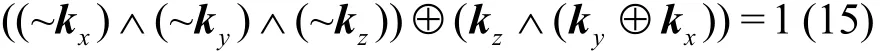
L集传播lp2xor((lx,ly) →lz)满足

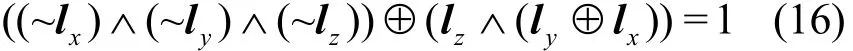
定义 9 三异或操作x⊕y⊕z=t，输入x,y,z∈(F2)m。经过三异或操作的K集传播kp3xor((kx,ky,kz) →kt)满足

L集传播lp3xor((lx,ly,lz) →lt)满足

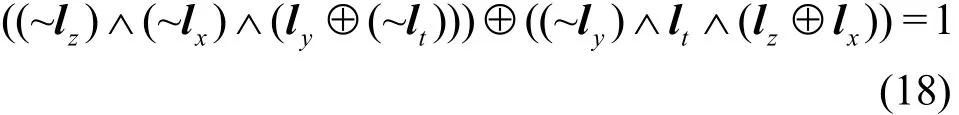
定义10 与操作x∧y=z，输入x=(x0,x1,… ,xm−1),y=(y0,y1,… ,ym−1)∈ (F2)m。经过与操作的K集传播kpand((kx,ky) →kz)满足

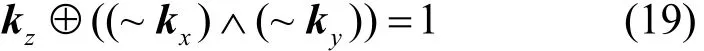
L集传播lpand((lx,ly) →lz)满足

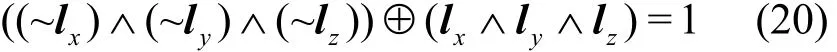
3 ARX结构可分性质模型

模加运算是ARX结构分组密码算法中唯一的非线性部件。常规模加运算输入x,y∈ (F2)m，模加运算输出z∈(F2)m，满足z=(x+y) mod2m。在某些ARX结构分组密码算法（HIGHT、TEA、XTEA等）中，存在一种常数模加运算，其输入变量y为常数（轮密钥），满足z= (x+rk)mod2m。

3.1 常规模加运算模型

常规模加运算输入x,y∈(F2)m，输出z∈(F2)m满足

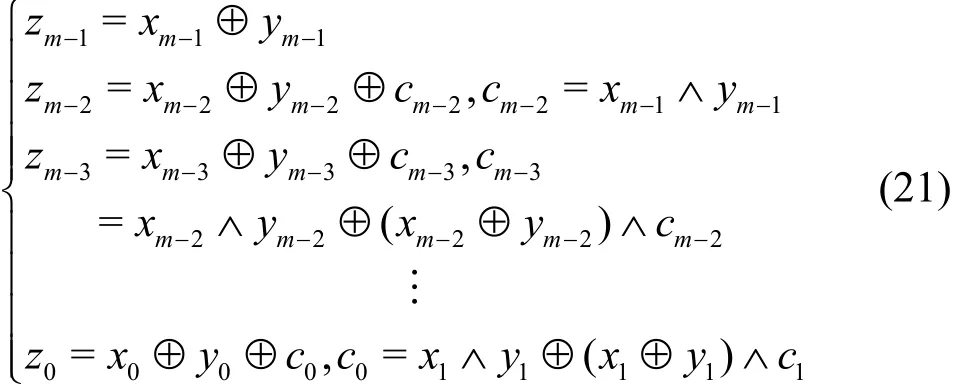
其中，是模加运算的进位。常规模加运算K集传播过程如表1所示。

增加 12个变量辅助表示模加运算K集传播，满足

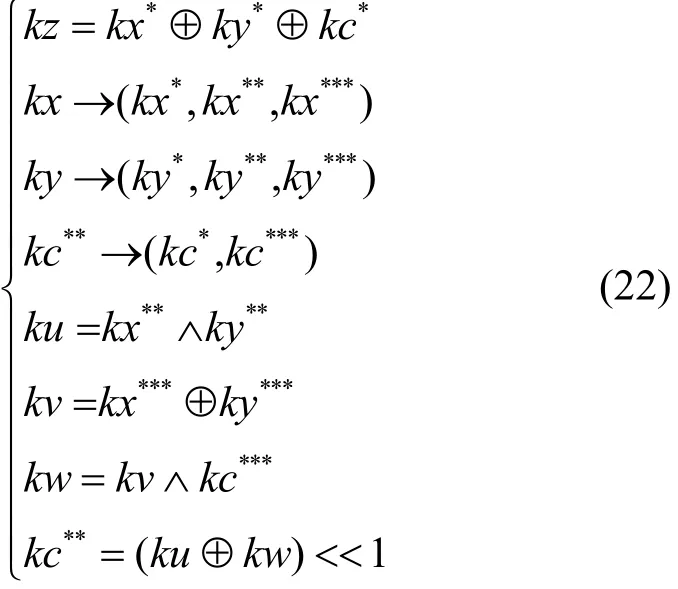
其中，8个比特为0的分支状态。因此，在K集传播过程中该8 bit限制为0。常规模加运算K集传播系统Sk+((kx,ky)→kz满足

根据K集传播过程，可得到常规模加运算L集传播系满足

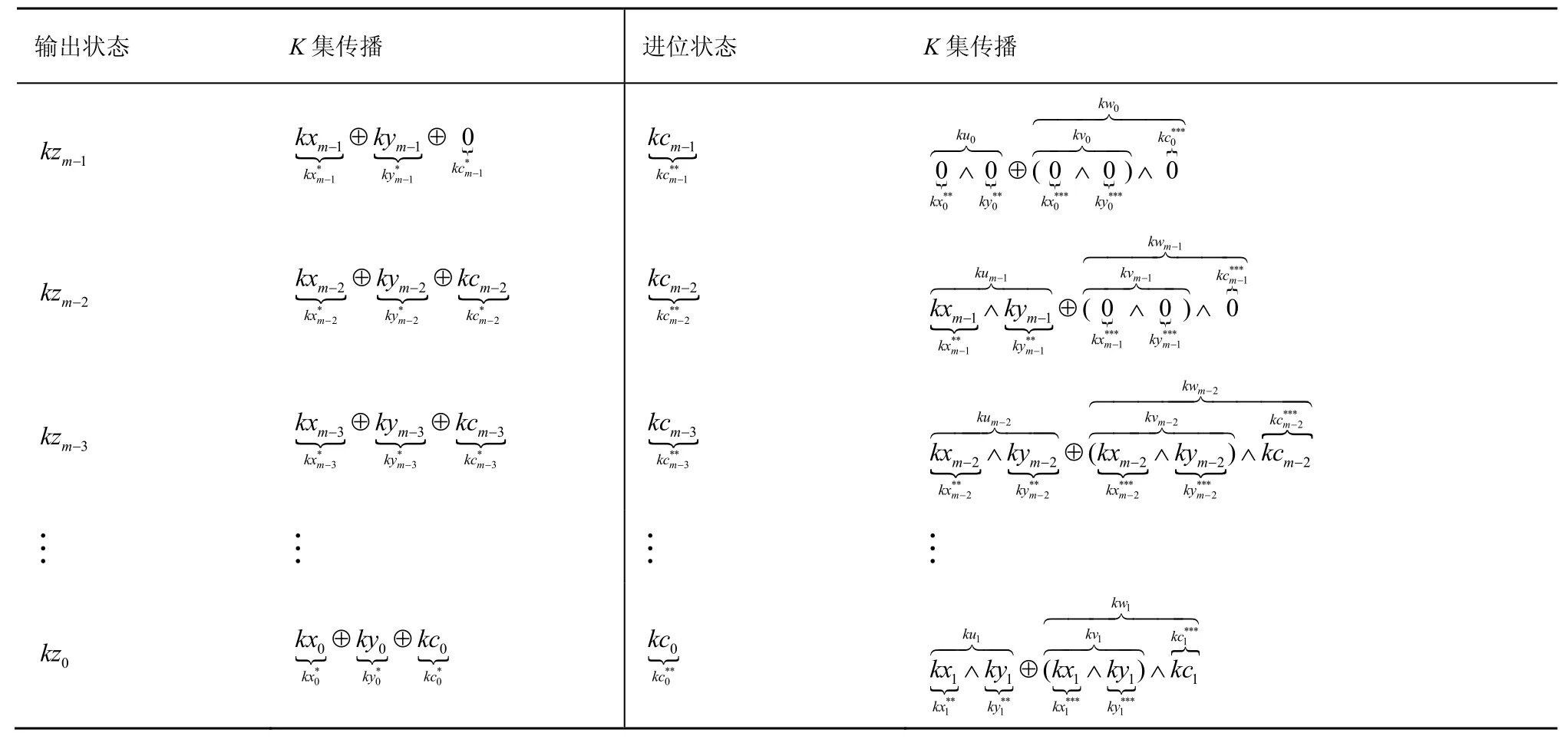
表1 常规模加运算K集传播

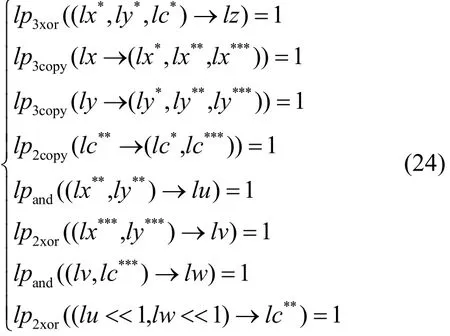
3.2 常数模加运算模型

常数模加运算输入x,rk∈ (F2)m，输出z∈(F2)m满足

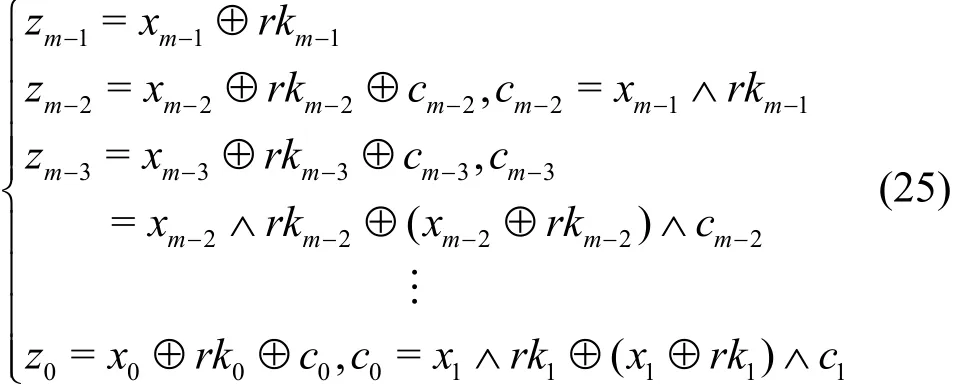
其中，c=(c0,c1,… ,cm−1)∈ (F2)m是模加运算的进位。由于轮密钥为常数，则轮密钥的三子集积分可分性质满足= (0,0)。常数模加运算K集传播过程如表2所示。

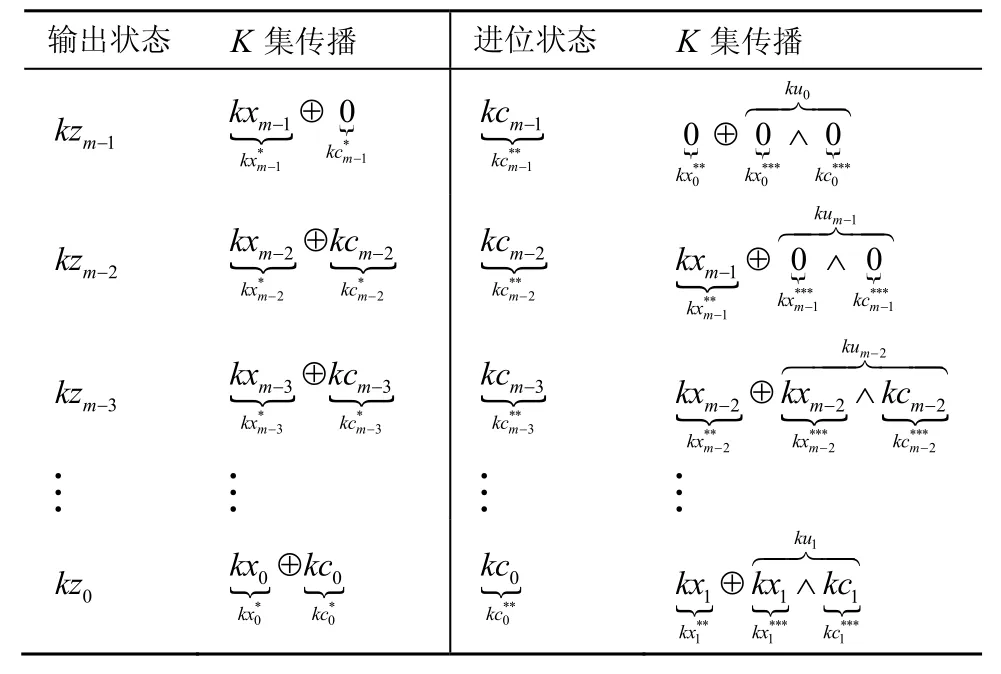
表2 常数模加运算K集传播

增加7个变辅助表示常数模加运算K集传播，满足

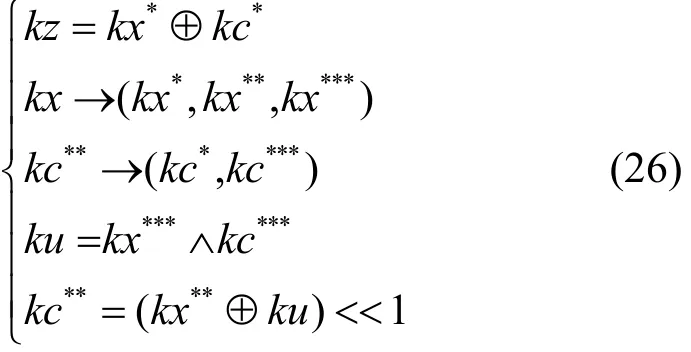
其中，5个比特为0的分支状态。因此，在K集传播过程中该5 bit限制为0。常数模加运算K集传播系统Sk+c((kx,krk)→kz满足

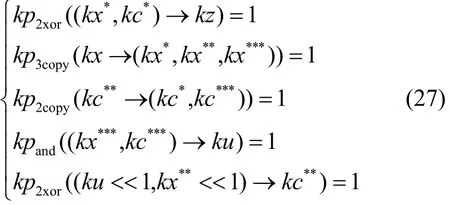
根据K集传播过程，可得到常数模加运算L集传播系统Sl+c((lx,lrk)→lz满足

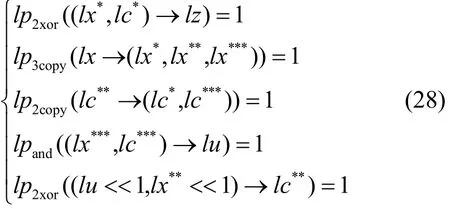
3.3 搜索算法

根据三子集可分性质经过“分支”“异或”“与”及“模加”操作的传播规则，SAT/SMT求解器可以建立 ARX结构分组密码轮函数的积分传播模型。由三子集可分性质经过ARX结构轮函数传播路径，可建立r轮积分传播系统。K集和L集传播过程中满足一定传播条件，可通过L集过滤算法减少L集中的冗余向量从而降低搜索时间复杂度。给定输入集合X满足三子集积分 (k,l) =(K0,L0)，对于r轮输出集合Y满足三子集可分性质，如果Kr集中包含m个相异的单位向量，则不存在以(k,l)积分特征为输入的r轮积分区分器。如果Kr集中不存在某单位向量ei，对任意k∈Kr满足 ⊕y∈Yπei(y)=0，则r轮输出的第ibit为平衡比特。积分自动化搜索算法的具体描述如下。

1) 初始化参数。给定三子集输入积分，初始化平衡集合Bset为空集，不确定集合Uset为空集。

2) 建立模型。根据三子集可分性质，通过 ARX结构分组密码轮函数Fr传播规则，利用SAT/SMT求解器建立满足积分传播路径的r轮积分传播系统。

3) 求解。利用SAT/SMT求解器求解r轮积分传播系统。如果存在一组解满足步骤2)的传播条件，添加集合{i|i∈ [0,m− 1]}到Uset，并判定不存在以(k,l)积分特征为输入的r轮积分区分器。否则对所有i∈ [0,m− 1]测试ei是否满足ei∈Kr，如果满足则添加i到Uset中并继续测试，否则，添加i到Bset中并继续测试。最后添加到积分区分器集合ID中。

4) 搜索所有可能的积分区分器。遍历所有可能的 三 子 集 输 入积分(k,l)， 满 足wt(l) =m−1,wt(k)=m，执行步骤1)～步骤3)，最终输出积分区分器集合ID。

在建立模型的过程中，会有大量的冗余L集向量产生，但冗余L集向量并不会影响K集向量传播，因此，冗余的L集向量可通过筛除算法筛除或不做任何处理。经过模加轮密钥操作时，L集所有向量均影响K集的向量传播，利用L集扩展算法扩展L集向量并添加到K集中。该算法的时间复杂度为O(m2)，数据复杂度O(1)，空间复杂度为O(1)。其中，L集向量筛除算法SieveL的具体描述如下。

1) 初始化参数：三子集积分变量(K,L)，积分向量元素长度m。

2)L集向量筛除。SAT/SMT限制语言描述如下。

①初始化空命令字串

②向空字串添加否定断言

③foriin (0,m)

④ ifi==m−1

⑤ 向命令字串添加命令“BVGE(L[i∶i],L[i∶i])”

⑥ 返回

⑦ else

⑧ 向命令字串添加命令“BVGE(L[i∶i],L[i∶i]) AND”

L集扩展算法ExtendL的具体描述如下。

1) 初始化参数：L集积分变量，临时变量k，积分向量元素长度m。

2)L集扩展。SAT/SMT限制语言描述如下。①初始化空命令字串

②向空字串添加赋值断言

③foriin (0,m−1)

④向命令字串添加命令“(ifL[i∶i] == 0b1 then 0 else BVXOR(L,1＜＜i) end if) ork=”

⑤向命令字串添加命令“(ifL[m−1∶m−1] == 0b1 then 0 else BVXOR(L,1＜＜(m−1)) end if) )”

4 应用

本文基于 STP[11]求解器实现积分区分器自动化搜索，平台搭载 Intel(R) Core(TM) CPU i5-4210M (2.6 GHz, 1 GB RAM, Ubuntu14.04.1)。

4.1 SIMON

SIMON簇分组密码算法是由NSA提出的一种轻量级分组密码算法。SIMON采用类Feistel结构，分组长度为2n，表示为 SIMON-2n，字节长度n∈ {16,24,32,48,64}。SIMON分组密码轮函数表示为

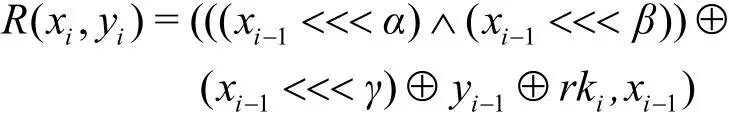
其中，循环移位常数α=8、β=1、γ=2。SIMON簇分组密码算法轮函数如图1所示。

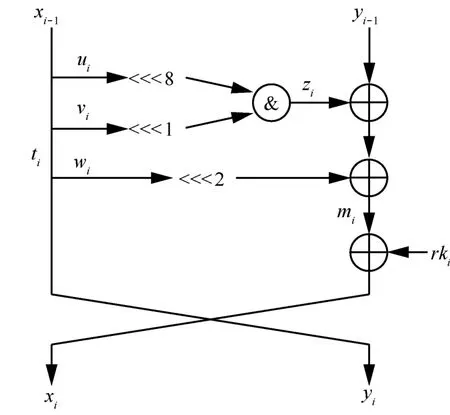
图1 SIMON簇分组密码算法轮函数

SIMON轮函数，输入集合X满足三子集可分性质。根据三子集传播规则，K集传播满足

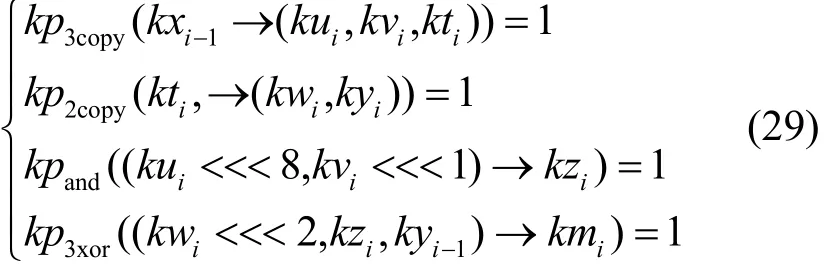
L集传播满足

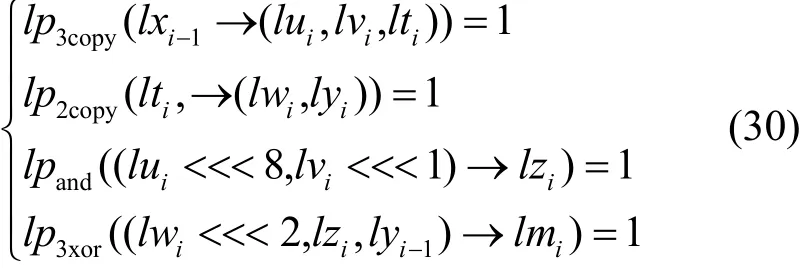
经过异或轮密钥操作时，对L集变量lxi扩展为辅助变量ktempi，并将变量和赋值给。轮函数输出三字集满足利用该搜索算法，SIMON分组密码积分区分器如表3所示。

表3 SIMON分组密码积分区分器

4.2 HIGHT

HIGHT分组密码算法是由 Deukio等[8]在CHES2006中提出的一种轻量级分组密码算法。HIGHT分组密码长度为64 bit，密钥长度为128 bit。HIGHT分组密码算法轮函数如图2所示。

图2中的Ft,t∈ [0,1]函数定义为

HIGHT轮函数K集传播变量mi,j,j∈ [0,3]传播经 过 函 数Ft到ni,j,j∈ [0,3]， 当t=0时 满 足(α,β,γ) = (1,2,7)，当t=1时满足(α,β,γ) = (3,4,6)。需要增加额外的 6个变量

来描述K集传播，满足传播系统SFt(km→kn)

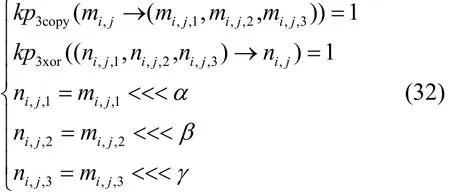
由于模加运算输入变量ni,j,j∈ [0,3]需要额外增加3个变量描述模加积分传播，且满足则K集传播时可以省略3个额外变量以降低搜索时间复杂度，HIGHT轮函数K集传播满足传播方程

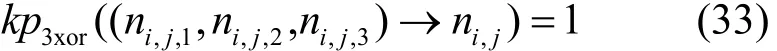
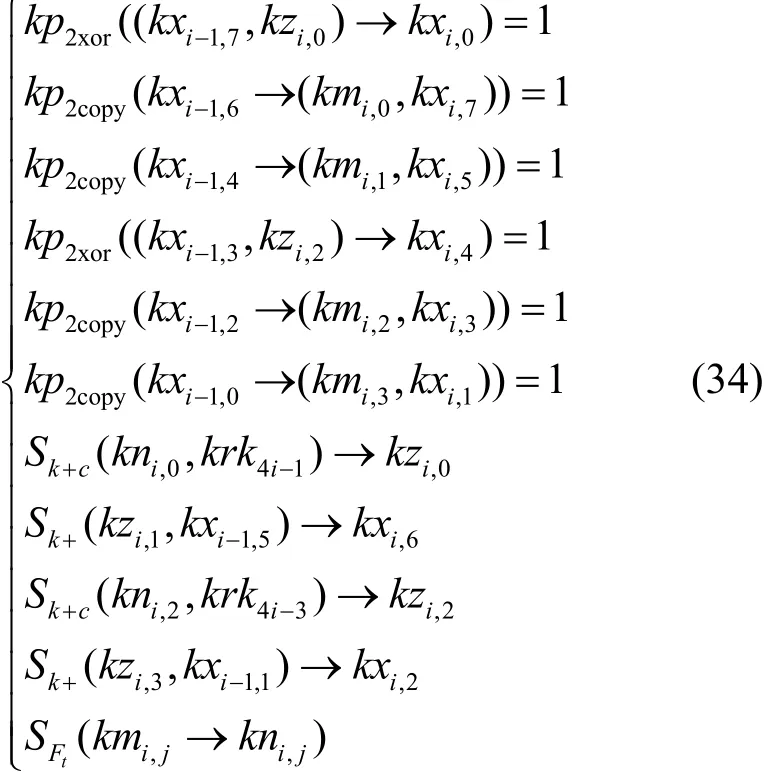
L集传播过程中3xor与3copy操作时不等价，经过Ft函数后3个额外变量不能省略。HIGHT轮函数L集传播同K集传播方程。经过异或轮密钥操作时，对L集变量lni,1、lni,3扩展为辅助变量ktempi,1、ktempi,3，并将辅助变量ktempi,1、ktempi,3分别赋值给kni,1、kni,3。轮函数输出三字集满足L集向量筛除规则。利用该搜索算法，HIGHT积分区分器如表4所示。

表4 HIGHT积分区分器

4.3 其他算法

利用该算法搜索得到，SIMECK簇分组密码算法[12]SIMECK32/48/64分别存在14、17和20轮积分区分器；SPECK簇分组密码算法SPECK32/48/64/96/128存在6轮积分区分器；LEA分组密码算法存在8轮积分区分器。

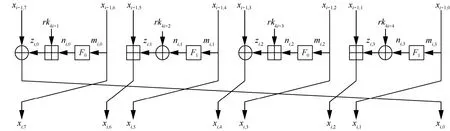
图2 HIGHT分组密码算法轮函数

5 结束语

本文提出一种基于 SAT/SMT求解器自动化搜索 ARX结构分组密码积分区分器的方法。利用三子集积分可分技术，通过建立缩减轮数的ARX结构分组密码算法积分传播系统，求解得到缩减轮数的积分区分器，并对所有版本的 SIMON32/48/64/96/128算法进行三子集积分区分器搜索，分别得到14、15、17、21和25轮积分区分器，进一步精确了Todo提出的SIMON积分界。利用该算法，搜索得到8条18轮HIGHT积分区分器。

SAT/SMT求解器同样能够应用到SPN结构及Feistel结构分组密码算法中，但不能有效完整地描述大状态S盒积分传播规则。如何自动化搜索大状态S盒积分传播，是未来需要研究的工作。

[1] TODO Y. Structural evaluation by generalized integral property[C]//EUROCRYPT. 2015∶ 287-314.

[2] TODO Y. Integral cryptanalysis on full MISTY1[C]//CRYPTO. 2015∶413-432.

[3] WANG Q J, LIU Z Q, KEREM V, et al. Cryptanalysis of reduced-round SIMON32 and SIMON48[C]//INDOCRYPT. 2014∶143-160.

[4] TODO Y, MORII M. Bit-based division property and application to simon family[C]//Fast Software Encryption. 2016∶ 357-377.

[5] ALEX B, ARNAB R, VESSELIN V. Differential analysis of block ciphers SIMON and SPECK[C]//Fast Software Encryption. 2014∶546-570.

[6] XIANG Z J, ZHANG W T, BAO Z Z, et al. Applying MILP method to searching integral distinguishers based on division property for 6 lightweight block ciphers[C]// ASIACRYPT. 2016∶ 648-678.

[7] SUN L, WANG W, LIU R, et al. Milp-aided bit-based division property for arx-based block cipher[M]. IACR Cryptology ePrint Archive,2016.

[8] DEUKIO H, JAECHUL S, SEOKHIE H, et al. HIGHT∶ a new block cipher suitablefor low-resource device[C]//Cryptographic Hardware and Embedded Systems. 2006∶ 46-59.

[9] DEUKIO H, JUNG K L, DONG C K, et al. LEA∶ a 128-bit block cipher for fast encryption on common processors[C]//WISA. 2013∶ 3-27.

[10] DAVID J, WHEELER, ROGER M. Tea, a tiny encryption algorithm[C]//Fast Software Encryption. 1994∶ 363-366.

[11] YAO J T, LIU W N. The STP model for solving imprecise problems[C]//GrC. 2006∶ 683-687.

[12] YANG G Q, ZHU B, VALENTIN S, et al. The simeck family of lightweight block ciphers[C]//Cryptographic Hardware and Embedded Systems. 2015∶ 307-329.