基于紧框架的二阶总广义变分图像修复模型

董卫东，彭宏京

DONG Weidong,PENG Hongjing

南京工业大学 计算机科学与技术学院，南京 211816

Computer Science and Technology,Nanjing University of Technology,Nanjing 211816,China

1 引言

图像是现实生活传递信息的重要媒介，对获取的图像信息进一步处理是人类正确认识客观世界的必要途径。图像修复是图像处理和分析领域的一个重要应用，其目的在于提高图像获取和传输过程中受到破损的图像质量。该类问题在数学意义下为典型的反问题，需要通过建立合适的数学模型，并设计求解优化算法得到最终的修复结果。Chan等人提出著名的TV修复模型[1]，比传统各向同性扩散方法更加有效地保持图像的边缘结构，且模型数值计算简单，并具备严格的收敛性。但TV模型在修复过程中将图像建模为分片光滑的，会出现明显的“阶梯效应”。 小波及其多分辨分析理论的兴起，很大程度上推动了图像表示方式的发展。Chan等人[2]研究了基于变分的小波修复方法，在修复图像的同时，一定程度上改善了图像边缘信息模糊且平坦区域过光滑的现象，但模型仍采用基于时间迭代的处理算法，收敛较慢，导致模型运算效率较低。Chan R等[3]提出一种利用交替迭代的小波域修复优化算法，大大提升了图像处理效率。然而这类方法仍是基于有界变差函数空间的正则化模型，“阶梯效应”现象无法避免。 2010年，Bredies等提出了一种新的数学变分模型[4]，即总广义变分（TGV），其是传统有界变分的继承与发展。不同于传统TV模型将图像建模为分片常数函数，TGV能够有效地逼近任意阶的多项式函数，并具有凸性和旋转不变等优良特性，能够很好地对图像进行建模分析。许建楼等在TV小波修复模型的基础上，采用TGV对图像正则化项进行约束，建立基于TGV的小波修复模型[5]。该模型能够有效减轻传统TV模型易产生阶梯效应的不足，但对于细节信息较多且含有纹理成分的图像修复效果并不理想。近年来紧框架系统理论及其优化算法的快速发展[6]使其在图像处理领域的应用获得重视，Cai等[7]利用紧框架变换的冗余特性建立图像去卷积正则化模型，并采用分裂算法对模型求解，有效改善了图像恢复过程细节信息易产生模糊的现象。Rosemin等[8]对小波变换和紧框架变换在CT与MRI图像融合中的应用进行了对比分析，尽管小波变换是图像信号处理分析方面的重要工具，但其冗余和平移不变等特性的缺失，大大限制了其在图像稀疏表示中的作用。与经典小波变换不同，紧框架系统由一组对称或反对称的小框架函数共同构成，当应用到图像变换中时，其能够根据不同图像或同一图像不同区域的具体结构特征来获得图像最佳的稀疏表达方式，从而准确地描述图像信息。

鉴于紧框架系统具备的优良特性，本文提出一种新的基于紧框架变换的TGV图像修复模型，并给出了结合分裂技术和原始-对偶方法的优化求解算法。一方面该模型兼具了TGV模型的优点，克服了有界变差空间不满足人眼“连通性原则”的缺陷，避免了图像平坦区域过光滑的现象。另一方面，通过紧框架下图像的稀疏表示，降低了图像数据处理的规模，提高了模型计算效率。多层紧框架分解后，图像不同尺度多个方向的特征信息使得原图像不同区域的结构信息都能得到完备表达，进而图像修复过程中一些微小纹理及细节信息能够获得有效保护。实验结果显示，本文模型的修复效果、峰值信噪比、平均绝对误差和结构相似测度的计算结果与TV小波修复模型[9]及二阶TGV小波修复模型[10]相比均有提升。

2 紧框架变换

对于一个可数集合X⊂L2(R)，被称为L2(R)上的紧框架[11]，当且仅当：

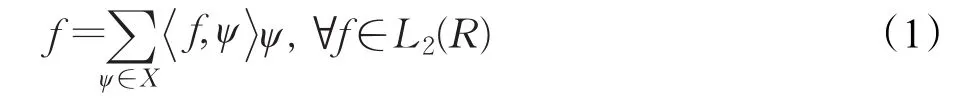
且，称为小框架函数。紧框架系统X(ψ)由多个ψi通过伸缩平移得到，即：

不同于小波变换只有唯一的小波函数，紧框架系统具有一组小框架函数。

紧框架变换可以根据UEP原则通过多分辨分析获得[12]，由多分辨率分析的理论可知，要构造一个紧支撑的框架系统，首先需要一个紧支撑的尺度函数φ∈L2(R)，对应于一个尺度模板函数（即低通滤波器组）ζφ，并且满足二尺度方程：（傅里叶变换），ζφ是一个三角多项式，且ζφ(0)=1。紧支撑的小框架函数，对应于一个高通滤波器组，满足为三角多项式。由UEP可以得到，生成框架系统所需要的尺度函数和小框架函数应当满足：

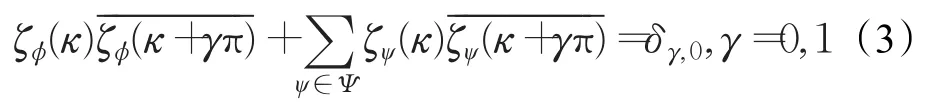
若尺度函数对称，则生成的框架系统也是对称的，且具有线性相位，该特性十分重要[13]。在图像数据分析中，当尺度函数和小波函数作为滤波函数，且滤波器具有线性相位时，能有效避免图像信号在分解与重构中的失真，最终保证图像修复效果的改善。

对离散图像序列进行处理时，W∈ℝm×n,m≥n代表分解算子，即紧框架变换，WT代表重构算子，根据UEP原则，有WTW=I，但WWT≠I，对应的图像重构过程：u=WTWu。为更完备地描述图像的细节信息，需对图像进行多层框架分解，得到图像不同尺度多个方向的特征信息。记图像序列u的L层框架分解为：

其中Γ代表每一层框架分解所包含的不同方向，Wl,ju代表第l层分解的第 j个方向的子带图像小波框架系数。

传统的TV模型对图像像素的处理只是基于垂直方向和水平方向，而小波变换后则能得到图像小波域中水平、垂直及对角线三个方向的子带图像；当采用本文的紧框架对图像进行变换时，则可获得八个不同方向的子带图像。如图1和图2，分别对图像做四层双正交小波分解与紧框架分解的对比实验。相比于传统双正交小波变换，本文的四层紧框架变换能够获取图像每一层八个不同方向上的特征信息来对图像进行约束，可更好地完备表达图像特征，从而实现对图像细节及一些纹理信息的保护。

3 基于TGV的小波图像修复

利用TV作为正则化项，建立能量泛函进行图像修复时，易在图像平滑区域产生虚假边缘，这是TV在对图像建模时的不足。Bredies等人发现了一种新的变分数学形式，即总广义变分（TGV）。TGV的定义形式如下：

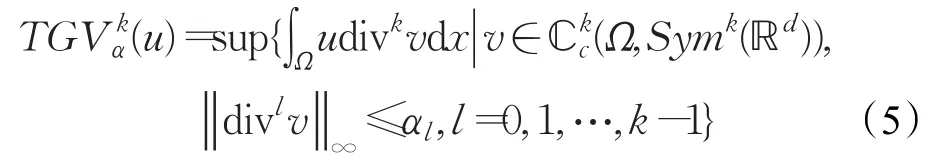
其中Symk(ℝd)代表ℝd上的k阶对称张量积，αl为固定的正常数，为紧支撑的向量空间。对于div1v，div2v散度分别定义为：

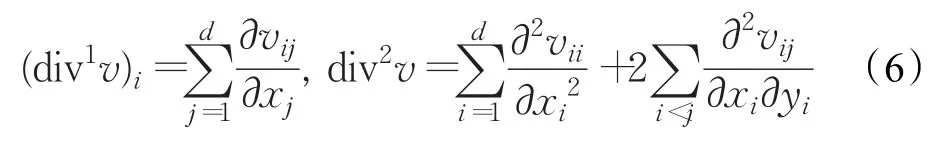
v的∞范数定义为：

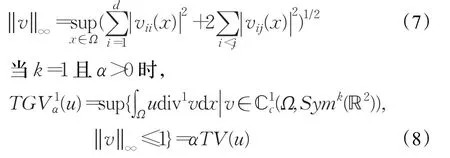
因此TGV可以看作TV模型的一般化。Bredies等通过理论推导得到式（5）的另一种表达形式[12]：

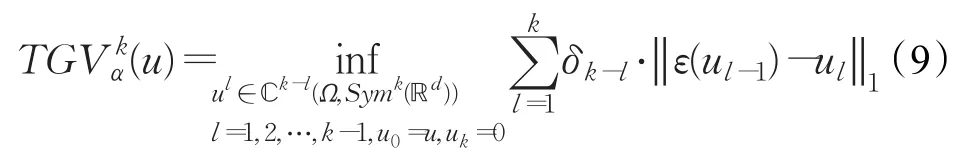
图1 四层双正交小波分解

其中ε(ul-1)为对称梯度算子，且

许建楼等提出了一种基于二阶总广义变分的小波修复模型：λ为调整参数，χi,j代表正交小波基，αi,j为待修复图像的小波系数，βi,j为恢复图像的小波系数。

与传统TV小波修复模型相比，它不仅兼具TV模型的优点，而且能够在修复过程中有效减轻“阶梯效应”。但其模型中选择的都是单一的小波基变换，无法实现对图像中不同区域结构信息的完备稀疏表达，因此极易造成图像中一些重要的细节信息无法得到有效修复。

4 本文模型及算法

4.1 本文模型

传统小波修复模型中只采用单一小波变换，由于自然图像特征的多样性，不同图像之间或同一图像不同区域间的结构特征也不尽相同，因此很难利用一种单一的小波基变换对所有图像进行完备描述。另外不同小波表达图像特征的方式各异，很难保证对传统小波修复模型中所选择的小波进行简单的替换而不影响模型算法的收敛性和稳定性，进而对图像修复效果产生影响。针对TGV小波修复模型存在的不足，提出了一种紧框架域下的二阶TGV图像修复模型，令，则：

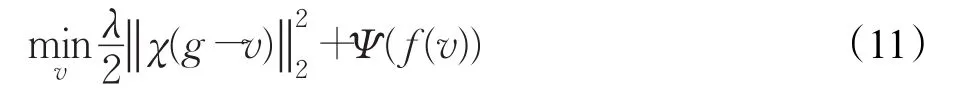
图2 四层紧框架分解

其中为紧框架变换，λ为调节参数，gl,j，vl,j为原始图像与观测图像的框架系数。模型中第一项为紧框架域下的拟合项，能够反映修复图像与原始图像之间的逼近程度。第二项为紧框架域下的二阶TGV正则化项，一方面紧框架变换后框架系数的低阶导数和高阶导数项得到有效平衡，另一方面紧框架的冗余性保证了其完备稀疏表达图像特征的能力。该模型不仅能够有效去除传统有界变差空间引入的不连通现象，保持边缘，而且对于一些重要纹理及细节信息的保护也比传统小波修复模型更为理想。

4.2 模型算法——PDSBA

由于模型（11）中的拟合项与正则化项都是非光滑函数，很难直接对目标函数进行最小化求解。模型通过引入辅助变量ξ，将式（11）转换为约束优化问题，即：

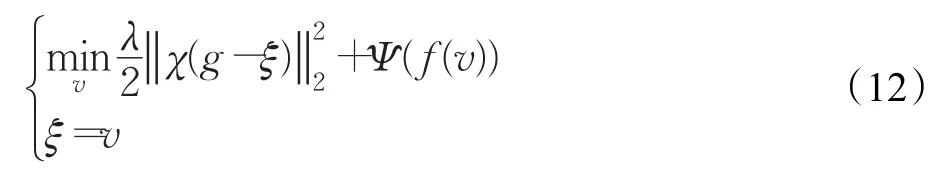
由简单罚函数方法将式（12）转化为易于处理的无条件约束最优化问题，即：

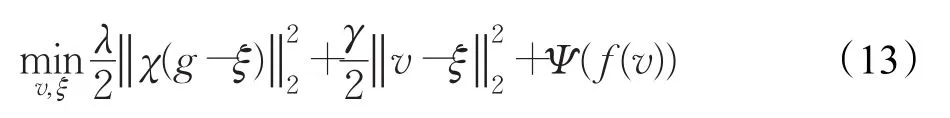
其中γ为大于0的参数。当γ→∞时，式（12）与式（13）等价。

对目标能量泛函表达式（13）的求解，近几年发展较快的基于变量分裂交替迭代的算法十分有效[14]。该算法的主要思想是将目标函数分裂为两个或多个易于处理的子问题，然后再进行交替迭代求解。

采用分裂技术将式（13）分裂为两个子问题：

式（14）的求解，通过得到对应的欧拉-拉格朗日方程：

令，W 为紧框架变换，将式（15）转换到图像域进行求解：

因此求解式（15），即可等价为求解：

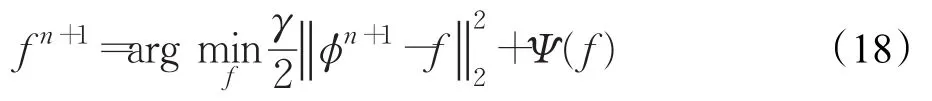
根据Legendre-Fenchel对偶变换理论[15]，给出式（18）的对偶形式：

表示一阶向后差分算子。

综上所述，可以得到模型式（11）的PDSBA算法：

（1）初始化参数 δ0,δ1,ω0,ωˉ0=0,p0,q0=0,τ,γ ，迭代次数MaxIt，迭代误差err；

（2）通过式（16）计算 ξk+1；

（3）式（20）计算 (pk+1,qk+1,fk+1,ωk+1,fˉk+1,ωˉk+1)，从而得到 fk+1；

（4）vk+1=Wfk+1；

（5）n=n+1；

（6）直到满足终止条件。

5 数值实验

实验中采用“Lena”和“Cameraman256”等图像进行测试。为比较不同算法图像恢复的能力，将本文算法与文献[9]基于TV的小波修复算法与文献[10]基于TGV的小波修复算法进行比较。为确保算法比较的有效性，对不同算法恢复质量的评价，本文不仅采用峰值信噪比（PSNR）、平均绝对误差（MAE）及结构相似测度（SSIM）的大小进行定量评价，也对图像修复结果中一些纹理与细节信息的复原情况进行定性分析。PSNR、SSIM值越大，MAE的值越小，则说明图像失真越小。

对于小波修复中的小波均选取Db7-9双正交小波，本文则采用紧框架变换。本文算法中的紧框架系统采用分段三次B样条的形式进行构造，得到一组低通与高通滤波器：

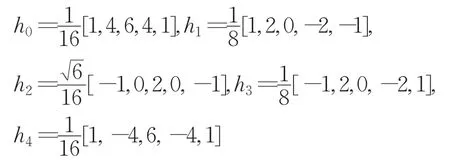
遵循UEP原则得到对应的尺度函数与小框架函数，如图3。

图3 基于分段三次B样条的紧框架系统尺度函数与小框架函数

双正交小波变换与紧框架变换的分解层数L=4，实验迭代终止条件设为，迭代次数100。将图像中随机丢失像素的比例记为PR，即图像破损率。实验评价指标PSNR、MSE、SSIM分别定义为：

m，n代表图像长和宽，μX,μY为图像均值，σX,σY为图像方差，σXY为图像协方差。

5.1 实验1

Cameraman256图像修复实验。图4（a）为原始图像，边缘以及细节信息较多，图4（b）为待修复图像，原始图像随机丢失40%的像素，噪声标准差为20。实验参数设置 γ=0.1，δ0=1，δ1=2，δ=0.1，τ=0.1。图4（c）为文献[9]基于TV的小波修复模型的结果，图4（d）为文献[10]基于TGV的小波修复模型，图4（e）为本文模型的修复结果。图5（a）到（e）分别为图4（a）到（e）的边缘信息。

图4 不同模型对Cameraman256图像的恢复性能比较

图5 不同模型对Cameraman256图像恢复结果的边缘信息对比

从图4的恢复结果中可以看出，图4（c）的恢复结果在相机支架及人衣服的边缘有明显的“阶梯效应”，而且对于地上的草地恢复十分模糊，大量信息丢失。图4（d）的恢复效果“阶梯效应”现象已基本消失，边缘信息也得到了很好的保护，但是对于一些明显细节信息，例如草地信息的修复较为模糊。而本文的修复结果图4（e）不仅可以有效去除“阶梯效应”，而且对于细节信息的恢复效果也较好。从图5的边缘恢复信息来看，图5（c）和图5（d）与原始边缘信息图5（a）相比，丢失了较多细节信息，而本文算法恢复的效果则与图5（a）比较接近。从定量方面分析，由表1可以得出，本文模型较文献[9]和文献[10]的模型都能获得较大的PSNR和SSIM以及较小的MAE，从而能够说明本文算法的优势。

表1 不同模型对图Cameraman256的修复效果对比

5.2 实验2

Lena图像修复实验。图6（a）为原始图像，边缘以及纹理信息较多，图6（b）为待修复图像，即原始图像随机丢失40%的像素，噪声标准差为20。实验参数设置γ=0.1,δ0=1,δ1=2，δ=0.1，τ=0.1 。图 6（c）为基于TV的小波修复模型[10]的结果，图6（d）为基于TGV的修复模型[11]，图6（e）为本文模型的修复结果。图7（a）到（e）分别对应于图6（a）到（e）的边缘信息。

图6 不同模型对Lena图像的恢复性能比较

从图6的恢复结果中分析，图6（c）的恢复结果在左侧较粗的竖条、人肩膀处及镜子的边缘均出现“阶梯效应”。图6（d）的恢复效果“阶梯效应”现象已基本消失，边缘信息也得到了保持，但对于一些细节信息，例如帽子上的一些细小纹理的恢复效果不够好。而本文的恢复结果图6（e）不仅有效去除了“阶梯效应”，而且对于像帽子上的细微纹理等细节信息的修复效果也很好。从图7的边缘恢复信息分析，文献[9]的方法和文献[10]的方法和本文模型对比，一定程度上都会丢失较多的细节信息。由表2可以得到，本文模型与文献[9]和文献[10]模型相比，都能获得较优的评价指标值，从而验证本文算法在边缘及细节信息恢复性能上的优势。

图7 不同模型对Lena图像恢复结果的边缘信息对比

表2 不同算法对图Lena修复效果的性能比较

5.3 实验3

为更好地说明本文算法的有效性和稳定性，原始图像丢失不同比例的像素值，即采用不同PR值时（30%～50%），将本文算法与文献[9]和文献[10]算法进行对比，实验结果如表3。从表3中可以看出，一方面当取不同PR值时，本文算法获得的PSNR和SSIM值都高于文献[9]和文献[10]的结果，MAE值则较小；另一方面通过比较发现当PR值提高时，本文算法受影响程度要比文献[9]和文献[10]算法小，从而验证了本文算法的有效性与稳定性。

算法复杂性分析：TGV模型的数值实现中采用的是图像的二阶微分，相比于传统TV模型的一阶微分运算稍微复杂一些。但一方面本文紧框架域下的图像稀疏表示，大大降低了图像数据的处理规模，一定程度上降低了算法处理的复杂性；另一方面通过采用基于分裂技术的快速算法，也能够有效提高算法的运行效率。如表4为本文算法与文献[9]和文献[10]算法对不同图像进行修复所需时间的对比。

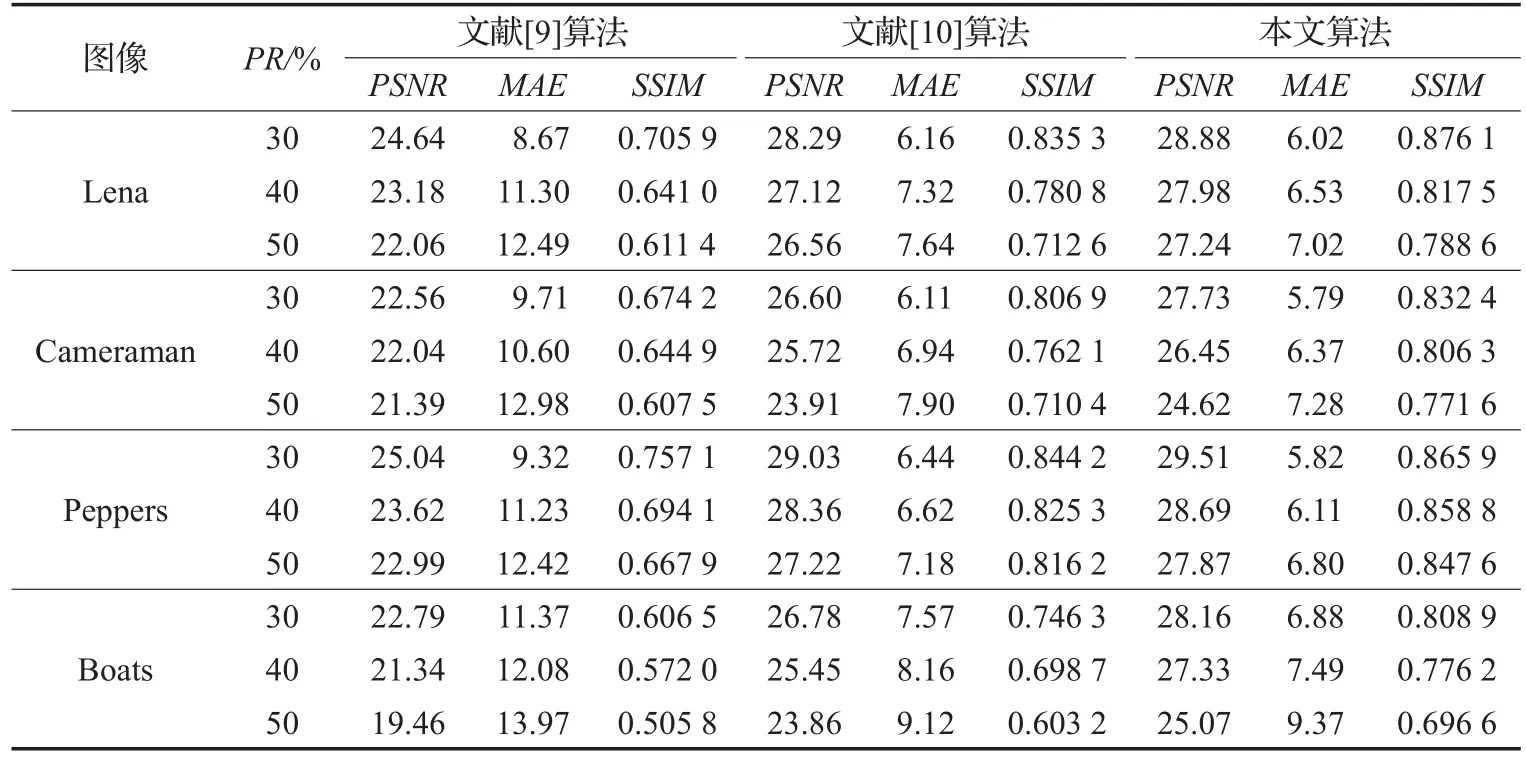
表3 不同PR时不同模型图像修复性能的比较

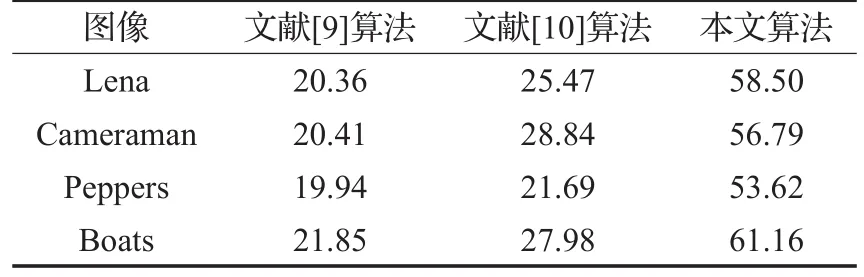
表4 不同模型图像修复的消耗时间对比s

由表4可以看出，本文算法消耗时间最长，主要由于四层紧框架分解后，每一层有8幅不同方向的子带图像，相比于四层小波分解后处理的12幅子带图像，本文算法实现时总共需对32幅图像进行处理，因此算法消耗时间相对较长。但时间的消耗得到了更加理想的图像修复效果，而且相比其他模型的消耗时间仍在可接受范围内，最终本文模型重在对于图像修复效果的提升。

6 结束语

由于自然图像特征的多样性，单一的小波基变换已经很难满足对图像信息的完备稀疏表达，从而导致修复过程中图像一些重要结构信息的丢失。具备冗余、平移不变等优良特性的紧框架系统的引入，有效地解决了这一问题，通过对图像的多层紧框架分解，得到图像不同尺度多个方向的特征信息，进而使得原图像不同区域的结构信息得到完备表达，最终建立合适的正则化模型。为有效求解该模型，采用分裂技术与原始-对偶方法相结合的算法，交替迭代求解两个易于处理的子问题，大大降低了算法的复杂度。实验结果表明，新模型不仅保边性能好，稳定性高，而且对于图像中一些重要的纹理和细节信息也能较好地修复。

参考文献：

[1]Chan T F，Shen J，Vese L.Variational PDE models in image processing[J].Notice of the AMS，2003，50（1）：14-26.

[2]Chan T F，Shen J，Zhou H.Total variation wavelet inpainting[J].Journal of Mathematical Imaging and Vision，2006，25（1）：107-125.

[3]Chan R，Wen Y W，Yip A.A fast optimization transfer algorithm for image inpainting in wavelet domains[J].IEEE Transactions on Image Processing，2009，18（7）：1467-1476.

[4]Bredies K，Kunisch K，Pock T.Total genneralized variation[J].SIAM Journal on Image Sciences，2010，3（3）：492-526.

[5]许建楼，冯象初，郝岩，等.二阶总广义变分图像修复模型及其算法[J].西安电子科技大学学报：自然科学版，2012，39（5）：18-23.

[6]Cai J，Chan R，Shen L，et al.Convergence analysis of tight framelet approach for missing data recovery[J].Advances in Computational Mathematics，2009，31（1）：87-113.

[7]Cai Jianfeng，Shen Zuowei.Framelet based deconvolution[J].Journal of Computational Methematics，2010，28（3）：289-308.

[8]Rosemin T J R，Priyadharshini A.A comparative analysis of CT and MRI image fusion using wavelet and framelet transform[J].International Journal of Engineering Research&Technology，2013，2（2）.

[9]Wen Y W，Chan R H，Yip A M.A primal-dual method for total variation-based wavelet domain inpainting[J].IEEE Transactions on Image Processing，2012，21（1）：106-114.

[10]许建楼，郝岩，张冀.二阶总广义变分小波修复模型[J].中国图象图形学报，2015，20（10）：1297-1303.

[11]Daubechies I，Han B，Ron A，et al.Framelets：MRA-based constructions of wavelet frames[J].Applied and Computational Harmonic Analysis，2003，14：1-46.

[12]Chan R，Riemenschneider S，Shen L，et al.Tight frame：An efficient way for high-resolution image reconstruction[J].Applied and Computational Harmonic Analysis，2004，17（1）：91-115.

[13]Chui C，He W.Compactly supported tight frames associted with refinable function[J].Appl Comput Harmon Anal，2000，8（3）：293-319.

[14]Goldstein T，Osher S.The split bregman algorithm for L1 regularized problems[J].SIAM Journal on Imaging Science，2009，2（2）：323-343.

[15]Chambolle A，Pock T.A first-order primal-dual algorithm for convex problems with applications to imaging[J].Journal of Mathematical Imaging and Vision，2011，40（1）：120-145.