结合半监督与主动学习的时间序列PU问题分类

陈 娟，朱福喜，2

CHEN Juan1,ZHU Fuxi1，2

1.武汉大学 计算机学院，武汉 430072

2.汉口学院 计算机科学与技术学院，武汉 430212

1.Computer School,Wuhan University,Wuhan 430072,China

2.School of Computer Science and Technology,Hankou University,Wuhan 430212,China

1 引言

时间序列是一系列按时间点取得的观测值，产生于许多自然或经济生产过程，如股票市场、医学、科学和自然观测[1-2]，一般可表示为序列T=t[1],…,t[j],…,t[n]。其中n表示其长度，t[j]表示时刻 j得到的观测值，T表示按时间顺序得到的观测值序列。

近年来，时间序列分类引起了国内外学者的研究兴趣。时间序列分类是指，基于已经标注的时间序列数据样本，构建数学模型，用于预测未知类别时间序列的类别，如在医学诊断中，通过患者与正常人的心率变化观测值（时间序列数据）作为训练集，构建数学模型，针对检查者的时间序列数据样本，通过数学模型判断其是否为患者。

一般分类模型总是通过足够的目标类(P)标注数据以及非目标类(N)标注数据进行有监督学习并构建分类器[1-2]，然而由于很多领域（比如医疗、工业应用中）对数据的标注代价过大，数据量的骤增进一步加大了标注数据的难度[3]。因此，出现了基于PU问题的分类，即通过少量标注的目标类(P)数据以及大量未标注(U)的数据，进行训练，从而得到一个分类模型。这种方法大大降低了人工标注数据量，从而有效减少了获取完整标注训练集的代价[4]。

在PU问题的分类中，由于训练集中仅包含目标类(P)的标注数据，不存在非目标类(N)的标注数据，导致通过有监督学习构建分类器的方式难以适用于其中。因此，有学者提出先采用半监督学习，获取足够的标注数据作为分类器的训练数据，再进行分类器的构建。其过程为：首先，以半监督学习对未标注数据集U中的数据进行自动标注；然后，以自动标注得到的数据集作为训练集，构建分类器[4-7]。然而，半监督学习对于分类平面附近的数据难以准确地自动标注，而恰恰这些数据对于分类平面的确立又至关重要。

针对上述问题，本文拟采用主动学习对PU问题中未标注数据集进行数据选择，选出边界数据样本并人工标注，以得到准确的标注训练集，从而以标注数据集进行分类器构建。本文的主要工作如下：

（1）将主动学习技术应用于基于PU问题的时间序列分类中，选择少量边界数据，通过人工标注，得到可靠标注训练集，继而构建分类器，实现精准分类。

（2）提出一种基于QBC（Query By Committee）度量数据样本不确定性的方法，作为主动学习的数据选择策略。

（3）提出一种结合主动学习与半监督学习的方法SAL，以获取足够多的标注训练数据。

（4）以主动学习选择得到的人工标注数据以及半监督学习得到的自动标注数据作为标注训练集，构建基于PU数据集的分类器，用于对未知类别数据进行类别的预测。

2 相关工作

Li Wei等[5]提出一种半监督学习框架用于对PU数据集构建分类器，从未标注数据集DU中选择与P类数据集最近邻的未标注数据样本u，标注为P类，迭代标注直至达到停止条件，其中停止条件根据P类数据集中最近邻数据对的相似性距离的变化趋势确定。

Ratanamahatana C A等[6]在Li Wei的文献[5]的基础上，进一步对停止条件进行研究，其停止条件通过后验式的方法进行确定。首先，将未标注数据集U中所有数据样本，根据与P类标注数据集中数据样本的相似性距离，依次加入P类标注数据集，并计算每个数据样本加入后的停止标准置信度，最后基于此置信度确定上述迭代过程的停止条件。

Nguyen M N等在文献[7-8]中，提出了LCLC（Learning from Common Local Clusters）的方法，即基于共同局部簇学习的方法，将未标注数据集划分为LP（Likely Positive）、LN（Likely Negative）、RN（Reliable Negative），与P一起作为训练集构建1NN分类器；文献[8]是在LCLC方法[7]上进行深入研究，针对LCLC方法中假设每个簇中数据样本的类别一致的问题进行了改进，提出了通过多次采用LCLC对未标注数据进行类别置信度计算，根据置信度将类别倾向不明确的数据样本从未标注数据集U中删除，最后以剩余的数据样本作为训练数据集，构建KNN分类器。

针对时间序列数据的PU学习问题，有学者利用Markov性质和“完全随机假设”设计出了正例未标Markov（Positive Unlabeled Markov，PU Markov）时间序列分类器。实验证明其算法能提高满足Markov性质的时间序列分类的效率。但该算法适用范围有限，且对最优分类方法的选择方式难以确定[9]。

张影提出利用已经标记的正类点、负类点以及基于所有点构造的Universum数据集，采用U-SVM进行训练。采用训练得到的模型，来标记可靠的正类点以及可靠的负类点，以生成新的训练集。通过迭代的方法来重复上述过程，直到满足某种迭代终止条件[10]。

主动学习关键在于数据的选择策略[3]。基于数据样本的不确定性，选择根据当前训练集最难以确定其类别的数据样本用于人工标注；基于数据样本对训练集构建分类模型的期望值，选择标注之后能够对当前训练集所构建的分类模型产生最大改变的数据样本，用于人工标注；基于数据样本对训练集构建分类模型的期望错误率，选择标注后能够对当前训练集所构建的分类模型产生最小期望错误率的数据样本；基于投票委员会QBC，根据训练集数据构建多个不同的分类模型，作为委员会（Committee），并对未标注数据集U中数据样本进行投票，以投票结果不一致性作为数据选择策略。

赵建华等在文献[11]中，提出了一种结合主动学习到半监督学习中的方法，通过主动学习选择信息量高的数据样本进行自动标注，主要是对问题规模进行了缩减，从其实验结果中可以得出，其准确率相对于该文中选择的半监督方法几乎没有提升，因为文中并没有通过人工标注信息量高的数据样本来保证正确性。

鉴于半监督学习方法在PU问题的应用过程中，自动标注难以确保对训练集中数据样本标注的正确性，从而影响所构建分类器的准确率，主动学习通过人工标注训练集中部分高信息量的边界数据样本[12]，能够更加精准地确立分类平面，从而提高分类器准确率，藉此本文对如何应用主动学习于PU问题进行研究，并提出了一种结合主动学习以及半监督学习[13]的方法。

3OAL算法

基于PU问题的分类方法关键在于如何正确标注未标注数据集DU中的P类、N类数据样本，而分类边界附近数据样本的正确标注则更具挑战性。半监督学习，作为一种常用于PU问题中标注数据样本的方法，在一定程度上能够实现对未标注数据样本的自动标注，但是其对分类边界附近的数据样本仍难以准确标注。因此，本文提出一种方法OAL（Only Active Learning），在时间序列的PU问题分类中，采用主动学习对未标注数据集中数据样本进行有选择性的标注，即选择分类边界附近的数据样本，进行人工标注，以解决数据样本标注不准确的问题。

3.1OAL算法流程

在基于PU问题的时间序列分类中，初始训练集仅含有少量标注的P类数据集DP，以及大量未标注的数据集DU，其中并没有N类的标注数据，因此本文主动学习选择数据过程分为两个步骤，即初始N类数据样本的获取与边界数据样本的获取。

本文算法模型如算法1所示。其主要步骤是：第一，获取准确标注的初始N类数据集DN，采用与文献[5]中找P类数据相类似的方法，即将未标注集DU中与P类数据最不相似的数据样本u选出，迭代进行人工标注，直至u的类别为N ，则DN={u}；第二，以DP、DN的并集L作为训练集，构建数据选择模型M；第三，根据M从未标注数据集DU中选择数据样本u，判断是否满足主动学习停止准则，若是，则停止主动学习过程；若不是，则人工标注u，加入L。迭代上述第二、三步，直到满足主动学习停止准则；第四，根据主动学习过程得到的标注训练集，构建分类器。

算法1

输入：输入初始DP、DU

输出：分类器

1.获取N类数据DN，得L=DP∪DN

2.基于L，构建数据选择模型M

3.根据M，选择数据样本u

4.while未达到停止准则

5. 人工标注u，加入L

6. 基于L，构建数据选择模型M

7. 根据M，选择数据样本u

8.end while

9. 根据L，构建分类器

3.2 构建数据选择模型M

针对基于投票委员会（QBC）方法[14]，根据时间序列的特点，构建多个不同的分类器C1,C2,…,CK，作为数据选择模型M，分别对未标注数据集U中数据样本进行类别概率预测，以不同分类器的预测结果计算数据样本的不一致性，结合数据样本的区域密度，作为主动学习的数据选择策略。本文方法与传统QBC方法有所区别的是，并没有直接根据多个不同分类器的投票结果进行计数从而分类，而是采用QBC的思想结合多个不同分类器对未标注数据样本的类别进行预测，并以此为据计算未标注数据样本属于每个不同类别的概率。

3.2.1 时间序列多分类器构建

针对时间序列是由一组随着时间变化的序列值，由于数据本身的误差，或者数据获取过程中的误差，将会导致每个时间点的数据采样会有误差波动。本文通过均值化，将原始时间序列作2-均值、3-均值等多均值转换，构建多个训练数据集，其中原始训练集中时间序列看作为1-均值转换，本文中均值指算术平均数。K-均值是指对时间序列的每个点，以当前点开始的K个时间序列采样点的算术平均数作为当前时间点的值。如K取2，原始时间序列 Torigin=[1.2，2.2，3.2，4.2]，则2-均值时间序列：

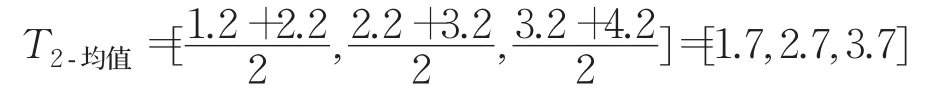
时间序如图1～3所示，分别表示数据集ECG[5]某个数据样本的1-均值、2-均值、3均值序列示意图，（a）图所示为两个P类数据样本，（b）图所示为一个P类数据样本、一个N 类数据样本，从图1～3中的（a）图可发现，随着均值的增加两个P类数据样本之间的距离在减小，尤其是波动较明显部分，如序列的最后几个数据采样；从图1～3中的（b）图可知，数据样本作多均值转换，并不会降低异类数据样本之间的距离，图中有差异的区域部分在图1～3均值序列下都保持着类似的距离差。

图1 ECG数据1-均值示例图

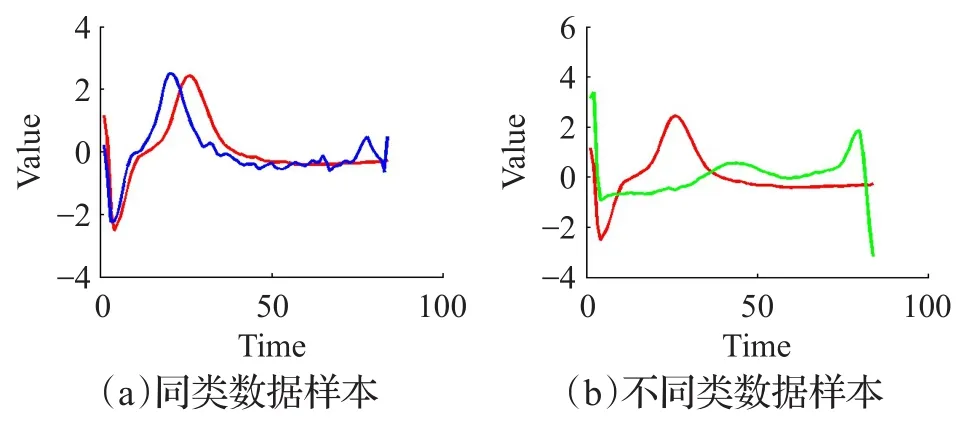
图2 ECG数据2-均值示例图

图3 ECG数据3-均值示例图

综上所述，时间序列的K-均值变换能够使得同类数据样本相似性距离更加小，同时不同类别数据样本之间相似性距离基本不变，其中相似性距离采用欧式距离度量[15]。因此，本文对原训练集进行1-均值、2-均值、…、K-均值变换，则可得到K个训练数据集，分别构建分类器得到K个分类器C1、C2、…、CK。

3.2.2 数据样本的不一致性Diff

对于i-均值变换得到的训练集Li，其中i的取值范围为[1,K]，对U中数据样本u作i-均值变换得ui，计算ui到Li中P类、N类的相似性距离：

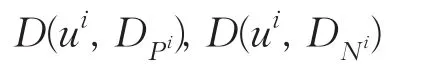
其中

ui与某类别的相似性距离越小，则ui是此类别的可能性越大。因此，定义ui属于P类、N类概率如下：

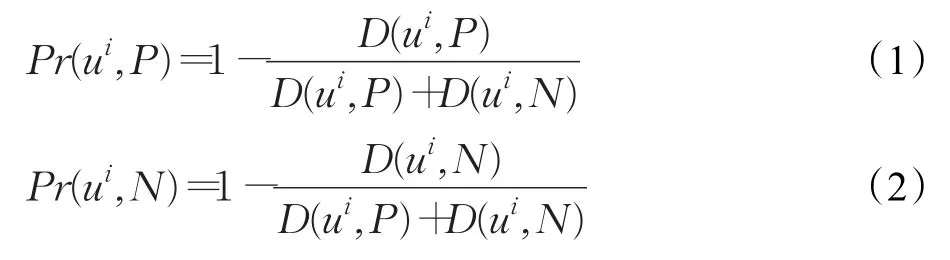
其中，

根据K个训练集的计算结果，采用QBC方法思路，通过多个分类器计算u属于不同类别的概率，定义数据样本u属于P类、N类的概率Pr(u,P)、Pr(u,N)如下：

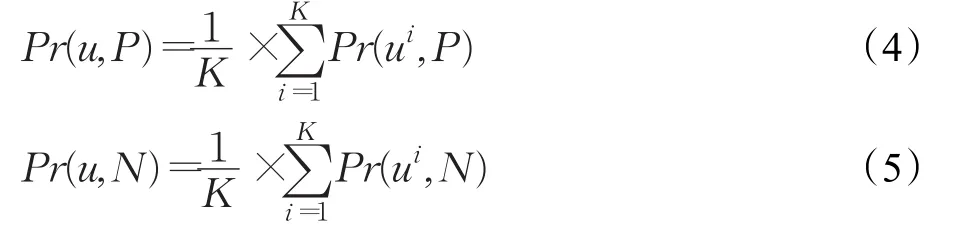
根据公式（4）、（5）定义数据样本u的不一致性，有：

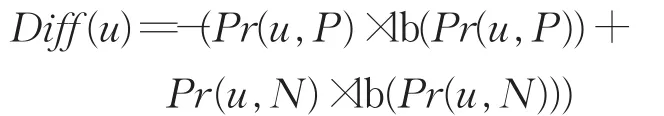
由式（3）可知 Pr(u,P)+Pr(u,N)=1，则 Diff(u)的取值范围为[0，1]，Diff(u)越大，u的一致性越差，则数据样本越应该被选择用于人工标注。

3.2.3 数据样本的区域密度Den

为了避免选择离异点数据，本文在考虑数据样本的类别不一致前提下，分析数据样本的密度，选择区域密度大的数据样本用于人工标注。本文仅在原始训练集中计算未标注数据样本的区域密度。数据样本u的区域密度通过其与近邻数据的相似性距离均值进行计算，定义如下：

其中，NNi表示数据样本u的第i个近邻数据样本，M表示取数据样本u的M个近邻数据样本进行区域密度的计算，本文中M 取值5。Den(u)越小说明其近邻数据样本与u越紧凑，从而表示u附近数据样本分布密度越高，标注数据样本u之后能够提供更多的有效信息。

3.2.4 数据选择参数Info

本文综合考虑上述两个因素，作为未标注数据样本的选择策略，定义如下：

Info(u)值越大，表现为数据样本u的分类结果一致性差，且所在区域分布密度高。因此，本文在主动学习过程中，选择Info值最大的数据样本用于人工标注。

3.3 停止准则

在完成上述3.2节的数据选择过程之后，计算被选择用于人工标注的数据样本u，是否能够提供有效的信息量。通过以u和标注数据集作为训练集，对训练集中剩余未标注数据样本进行最近邻分类，如果没有以u为最近邻的未标注数据样本，则停止主动学习，因为即使标注了u也不能对分类器的下一步构建提供有效信息量。

由于样本的选择是通过未标注数据样本不一致性和区域密度进行计算的，因此选择的未标注数据样本会逐渐趋向于P、N类的分类边界，在最坏的情况下，分类边界处的数据样本全部标注之后，上述停止准则也能满足。本文实验也证明了，在人工标注数据量占数据集比例25%以下停止准则就已经达到。

3.4 SAL算法

PU问题存在大量的未标注数据样本，仅通过主动学习选择数据样本用于人工标注，将会导致人工标注数据量过多，而且通过学习得到的标注数据量并不充足，因此，本文提出一种将主动学习与半监督学习相结合的SAL（Semi-supervised Active Learning）算法，进行数据标注。在主动学习过程中，结合半监督学习对部分数据样本进行自动标注，有效降低主动学习人工标注数据量的同时，增加最终训练分类器的标注数据量。

具体实现为，根据3.2.2节计算得到未标注数据集DU中所有数据样本的Diff值，选取最小的NUM个数据样本u1,…,ui,…,uNUM，根据Pr(ui,P)、Pr(ui,N)进行自动标注，前者大(Pr(ui,P)＞Pr(ui,N))则标注ui为P类，否则标注ui为N类，NUM为实验参数，具体由实验确定。

4 实验

4.1 分类器构建

基于PU问题的分类，其最终目的在于构建一个高准确率的分类器。通过本文提出的OAL或者SAL方法，或者半监督学习方法从未标注数据集U中获取足够多的标注数据，以获取的标注数据进行有监督学习，构建分类器，用于对未知类别数据样本进行类别预测。

对于通过学习得到的标注训练集，其中包括目标类(P)以及非目标类(N)的标注数据，本文构建分类器采用1NN方法，用于对未知数据样本进行类别预测，以测试本文方法的有效性。1NN分类方法作为一种经典的分类方法，被证明是高效的、易于实现的。很多研究表明，时间序列分类的最好分类结果来源于简单的最近邻分类（1NN）方法[15]。

4.2 数据集

实验数据分别采用 ECG、Word Spotting、Wafer、Yoga数据集[5]。实验数据如表1所示，其中，Training Set、Testing Set分别表示训练集、测试集；P、N 分别表示目标类、非目标类；如ECG数据训练集中含目标类数据样本208个，非目标类数据样本602个。

表1 实验数据集说明

4.3 实验说明

本文在实验中模拟人工标注过程，即将训练集分为标注集和未标注集，通过主动学习选择的数据样本，则加入标注集，并使用真实标注信息，而U中数据样本视为没有标注。通过主动学习得到标注数据集，再构建分类器，以分类器对测试集的分类效果检测本文方法的有效性。具体实现过程如下。

首先，训练集（Training Set）包括标注的正类数据集DP、未标注数据集U、负类数据集DN为空；其次，通过主动学习（OAL、SAL），将U 中部分数据进行标注，并根据标注的类别加入DP或DN。然后，以学习得到的DP以及DN，作为训练集，构建1NN分类器。最后，在对未知类别数据样本u进行预测类别时，计算u到{DPU DN}中所有数据样本的距离，以u最近邻数据样本的类别作为u的预测类别。

最终，分类效果则通过分类器对测试集（Testing Set）中数据样本进行类别预测，即以单个数据样本是否能够被正确分类为依据，进而根据测试集中所有样本是否被正确分类进行统计，以计算通过本文算法得到的标注训练数据集所构建的1NN分类器的分类效果F-measure。

4.4 结果分析

4.4.1 对比实验

首先，通过将本文方法OAL、SAL与2006、2008、2011、2012、2015年五篇针对时间序列PU问题进行研究的国际学术论文结果作对比，分析本文方法有效性，效果图如图4所示。其次，由于本文方法中需要人工参考标注过程，因此需要对人工标注量进行分析，OAL、SAL的人工标注比例如表2所示。

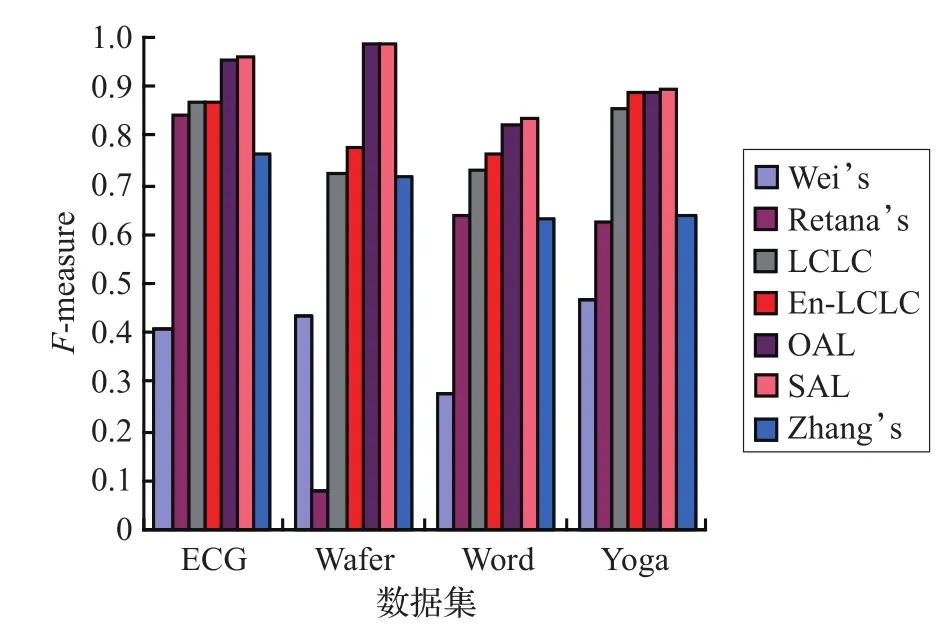
图4 不同方法的分类效果对比

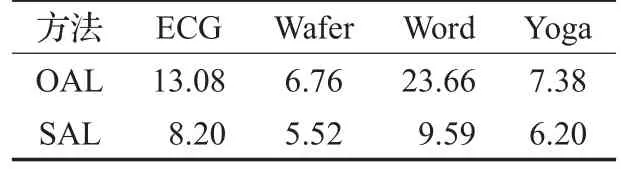
表2 人工标注量分析%

从图4中可知，OAL、SAL相对于上述五篇国际学术论文中提出的半监督学习方法，在数据集ECG、Wafer、Word的表现上，优势非常明显，且差异显著。在数据集Yoga上，相对于2006、2008、2015年的方法优势同样非常明显，而相比于2011、2012年基于聚类的半监督方法，分类效果也好。说明，本文方法OAL、SAL，由于人工标注了通过主动学习选择的边界数据样本，因此能够更加准确标注未标注数据集U中的数据样本，从而构建分类效果更好的分类器。

从图4可知，SAL方法在分类效果F-measure上与OAL不相上下，再从表2中所需人工标注量分析，本文SAL算法能够有效降低人工标注数据样本量。显然，由于SAL自动标注的数据样本不断加入，训练集中标注数据量更加充足，所能提供的信息量更多，从而需要的人工标注量减少，而边界附近的数据样本同样是以人工进行标注，因此也能保证未标注数据样本的标注正确性。从表2也可得出，本文方法SAL在提高分类效果的同时，能够将人工标注量有效控制在10%以内。

4.4.2 SAL方法参数实验

在SAL方法中，每次迭代都自动标注部分不一致性最小的数据样本，由于自动标注难以保证百分之百的准确性，过多地自动标注可能导致错误标注的出现，但是过少的自动标注又显得毫无意义。因此本文通过实验分析每次主动学习迭代过程中自动标注的样本数量。实验结果如图5所示。

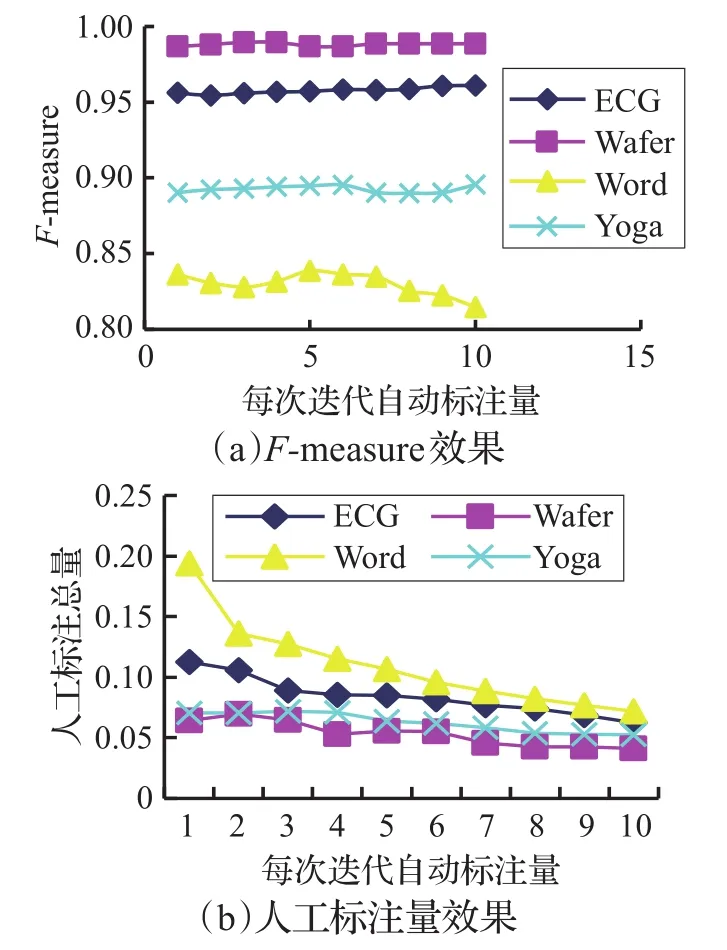
图5 SAL参数分析

从图5（a）中可知，随着自动标注量的增多，ECG、Wafer数据集的F-measure值基本保持不变。Yoga数据集呈现出略微的波动，但是整体上来说，并没有大的变化。而Word数据集随着自动标注量的增加F-measure有下降的趋势，自动标注量取值为5、6、7之后，F-measure呈下降明显。综上所述，说明不同数据集的数据分布不一样，从而使得自动标注的数据准确率不相同，即指ECG、Wafer与Yoga数据集不同类别数据样本分布区域离分类平面较远，因此自动标注数据样本的准确率高，从而即使增多自动标注数据样本也不会导致最终F-measure的下降，而Word数据集不同类别数据样本分布区域较分类平面近，从而自动标注过程更加容易出现误标注，随着自动标注量的增加而导致F-measure值下降。

从图5（b）可知，自动标注量的增加，人工标注量在减少。显然，自动标注的增加使得标注数据集的信息量加大，从而更早停止主动学习过程。自动标注量取值为5、6、7时，人工标注量开始趋于稳定。

综上所述，SAL方法中自动标注量参数取值为6，能够在降低人工标注量的同时，保持标注训练集的分类效果。

5 结束语

本文针对时间序列的PU问题分类，提出了基于主动学习的方法，通过少量的人工标注，得到正确标注的边界数据，从而训练出更加精准有效的分类器。由于人工标注的数据量有限，本文结合半监督学习与主动学习的方法，在进行人工标注的同时对数据样本自动标注，有效降低了在主动学习过程中人工标注量，并增加了标注训练数据量。

本文采用最近邻算法作为分类器的构建方法，应用主动学习于PU问题中相比半监督学习能够得到更好的分类效果，将继续研究如何将本文方法有效结合于某些复杂模型构建分类器如SVM，以使得分类效果更加突出。

参考文献：

[1]Xing Zhengzheng，Pei Jian，Yu Philip S，et al.Extracting interpretable features for early classification on time series[J].Knowledge&Information Systems，2012，31（1）：105-127.

[2]Arathi M，Govardhan A.Accurate time series classification using shapelets[J].International Journal of Data Mining&Knowledge Management，2014：39-47.

[3]Settles B.Active learning literature survey[R].University of Wisconsin-Madison，2010：127-131.

[4]刘露，彭涛，左万利，等.一种基于聚类的PU主动文本分类方法[J].软件学报，2013，24（11）：2571-2583.

[5]Li Wei，Eamonn K.Semi-supervised time series classification[C]//ACM Sigkdd International Conference on Knowledge Discovery&Data Mining，2006：748-753.

[6]Ratanamahatana C A，Wanichsan D.Stopping criterion selection for efficient semi-supervised time series classification[M]//Software Engineering，Artificial Intelligence，Networking&Parallel/Distributed Computing.Berlin Heidelberg：Springer-Verlag，2008：1-14.

[7]Nguyen M N，Li X L，Ng S K.Positive unlabeled learning for time series classification[C]//International Joint Conference on Artificial Intelligence，2011：1421-1426.

[8]Nguyen M N，Li X L，Ng S K.Ensemble based positive unlabeled learning for time series classification[C]//Database Systems for Advanced Applications，2012：243-257.

[9]张道坤.针对文本和时间序列数据的正例未标注学习算法研究[D].陕西咸阳：西北农林科技大学，2015.

[10]张影.基于SVM的PU问题与半监督问题研究[D].北京：中国科学院大学，2015.

[11]赵建华，刘宁.结合主动学习策略的半监督分类算法[J].计算机应用与研究，2015，32（8）：2295-2298.

[12]刘康，钱旭，王自强，等.主动学习算法综述[J].计算机工程与应用，2012，48（34）：1-4.

[13]陈荣，曹永锋，孙洪.基于主动学习和半监督学习的多类图像分类[J].自动化学报，2011，37（8）：954-962.

[14]陈念，唐振民.QBC主动采样学习在垃圾邮件在线过滤中的应用[J].计算机工程与应用，2014，50（22）：170-174.

[15]Serrà J，Arcos J L.An empirical evaluation of similarity measures for time series classification[J].Knowledge-Based Systems，2014，67（3）：305-314.