分时隙的比特转换RFID标签防碰撞算法

史长琼，夏广伟，严利辉

SHI Changqiong1，2,XIAGuangwei1，2,YAN Lihui1，2

1.长沙理工大学 智能交通大数据处理湖南省重点实验室，长沙 410114

2.长沙理工大学 计算机与通信工程学院，长沙 410114

1.Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation,Changsha University of Science and Technology,Changsha 410114,China

2.SchoolofComputerandCommunicationEngineering,ChangshaUniversityofScienceandTechnology,Changsha410114,China

1 引言

RFID射频识别技术（Radio Frequency Identification，RFID），是利用射频信号通过空间耦合实现无接触信息传递并通过所传递的信息达到识别目的，具有快速、实时准确的采集与处理信息的特点。RFID系统主要包括标签（Tag）和读写器（Reader）两部分，标签用于对象的身份识别，每个标签具有唯一的ID。阅读器用于接收标签信息，通过无线信号在可读范围内识别所有标签，广泛应用于自动识别系统，比传统的条形码更加方便、快速并且无需直接接触被识别物体[1-3]。在射频识别系统中，若有多个标签在同一时间响应阅读器将会发生标签碰撞，此时，阅读器无法快速识别出标签，标签必须在阅读器的查询指令下重新发送ID直到标签被识别，导致识别时间过长，严重影响识别效率[4]。

结合比特转换和分时隙的思想，本文提出一种基于比特转换的时隙二叉树RFID标签防碰撞算法（Bit-Conversion anti-collision algorithm based on Slotted Binary Tree，BC-SBT），通过将标签的原始比特进行转换，根据转换后比特碰撞位的不同，结合转换后比特的特点，分时隙响应阅读器的查询请求，阅读器收到标签发送的数据，直接还原出ID信息，从而减少查询次数并降低通信量。

2 相关工作

按照标签响应方式，防碰撞算法通常分为不确定算法和确定性算法两种[5]。不确定性算法大都基于Aloha机制，标签利用随机时间响应阅读器，如时隙Aloha、Frame-slotted Aloha算法等；确定性算法根据标签的惟一性选择标签进行通信，最常见的算法是树型搜索算法，包括二叉树算法、动态二叉树算法、查询树算法等。

2.1 Aloha算法

Aloha算法的基本原理是在识别过程中，阅读器检测标签的响应是否存在碰撞，如果存在，则阅读器发送终止命令，并且每个标签等待随机延迟时间来响应阅读器。根据不同的情况，基于Aloha的算法可以分为Slot-Aloha（SA）算法、帧时隙Aloha（FSA）算法和动态帧时隙Aloha（DFSA）算法[6]。由于Aloha算法识别标签的时隙比较简单，在少量标签的情况下性能良好。然而，时隙是随机生成的，所以存在一定的时间延迟，导致标签不可识别或不正确识别，即标签饿死情况[7]。而且，随着标签数量的增加，算法的性能也会下降。

2.2 二叉树搜索算法（BS算法）

树型搜索算法是一种确定性标签防碰撞算法[8-9]。该算法将阅读器查询范围内的多个标签ID进行逐位比较，直到成功读取该标签信息。文献[10]中，Wang Xue等提出二叉树搜索算法（BS算法），根据标签ID的信息所建的N叉查找树，并令N=2。标签根据碰撞信号的译码结果发出寻呼，每识别出一个标签就返回到起始点，是树型算法中的经典算法。其在识别过程中，将标签ID按照响应建立搜索树，以树的路径搜索叶节点来完成对标签的识别。同时，规定标签拥有唯一的ID，且电子标签需要准确同步，标签的序列号必须采用曼彻斯特编码。如图1所示，阅读器根据接收到的标签的应答，找到碰撞位，并据此向它们发送请求，采用二叉树查找的方法，可以根据每个标签ID号的不同将它们逐一区分开来。与基于Aloha的算法相比，树遍历算法不遭受标签饥饿，但是在面对长标签ID时仍然产生许多冲突时隙。并且不管是否存在树的碰撞节点，该算法会遍历整个二叉树，这将导致RFID系统的效率降低。

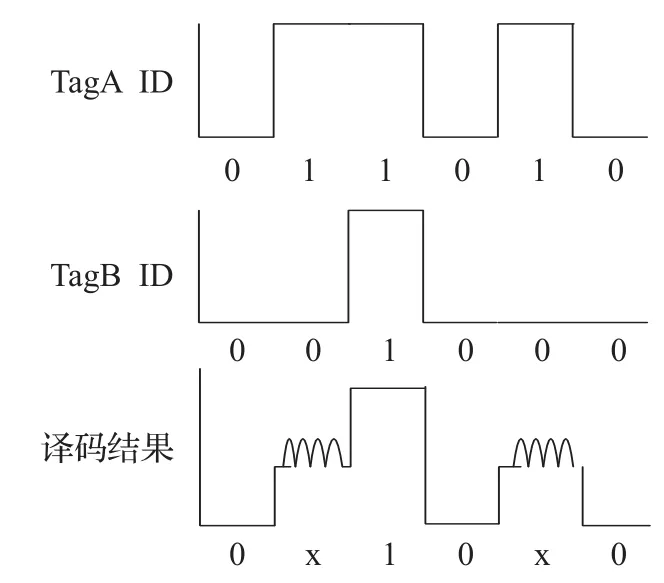
图1 编码碰撞识别示例图

2.3 4-ary询问树算法（4-ary QT算法）

文献[11]提出了4-ary QT算法，是一种基于询问树算法（QT算法）的改进算法。QT算法在识别过程中引入“终止”命令，一旦发生碰撞，则终止标签继续发送ID，阅读器以初始“0”或“1”开始查询，若以“0”开始，则阅读器以前缀“01”开始向范围内的标签询问，如果响应的标签碰撞，阅读器将串“01”增长为“010”继续询问，直到完全识别标签。当识别完所有以“010”为前缀的标签后，开始识别以“011”为前缀的标签。因此，查询树的内部节点为碰撞周期，叶子节点为空闲周期或成功周期。为了减少碰撞和查询次数，改进的4-ary QT算法结合了QT算法和时隙补偿机制，通过减少标签碰撞周期和空闲周期，来减少平均标签识别延时，并使用四叉查询树代替传统的二叉询问树。如果响应的标签发生碰撞，下次阅读器的询问串不像传统的QT算法那样增加1个二进制位，而是增加2位再进行询问。因此增加了询问树的宽度，减少了碰撞周期。在4-ary QT算法中，节点编码具有四种组合：“00，01，10和11”，并将记录分组到标签的原始编码，该算法改进了生成树的结构且消除了空槽。

基于树型的标签防碰撞算法不存在标签饿死情况，但此类算法查询次数多，识别时间过长，通信量大仍是限制系统效率的主要因素。因此，本文提出一种基于比特转换的时隙二叉树RFID标签防碰撞算法，结合了树型算法，并使标签分时隙响应阅读器的查询请求，通过设计一种新的反向编码转换规则，使得识别碰撞的过程更加高效。

3 BC-SBT（Bit-Conversion anti-collision algorithm based on Slotted Binary Tree）算法

改进的树型算法和Aloha算法虽然在一定程度上提升了识别效率，但仍然存在查询次数多，消耗时间长和冗余数据量大等局限性，致使系统的吞吐率和识别效率无法达到最优。本文融合分时隙思想和树型算法的优点，提出一种基于比特转码的时隙二叉树算法，该算法的原理是：首先设计转码规则，将标签ID识别码进行转换，响应阅读器查询请求，如果产生碰撞，则根据曼彻斯特编码规则，判断出碰撞位置，然后分时隙响应阅读器；最后，进行编码还原，最终达到识别标签信息的目的。

3.1 算法描述

在BC-SBT算法中，标签内部设有转码器，可以将标签的ID信息经过编码后发送给阅读器，例如：标签信息中分别含有“00，01，10，11”等编码，则经过反向编码转换后，其编码变为“1000，0100，0010，0001”，转码流程如图2所示。

图2 两位比特一组转换格式示例图

3.1.1 算法核心

根据以上转码规则，可将标签信息进行每2位比特一转，且经过转码后的每4位比特有且只有1个“1”，基于此特点，设置碰撞位第1位为“1”的标签在第1时隙响应，碰撞位第1位为“0”的标签在第2时隙响应。

基于比特转换的时隙二叉树防碰撞算法主要在以下方面进行改进：

（1）减少了查询次数和查询时间

阅读器发送寻呼指令之后，范围内的所有电子标签对此寻呼做出应答，本算法经转码后采用4位比特为一组的方式来进行识别，每组识别后，只需返回上次的碰撞节点并根据每4位比特有且只有1个“1”的规则判断下一组碰撞位置，进行下一组的识别过程，并不需要像BS算法和返回到根节点去发送寻呼识别其他电子标签；而4-ary QT算法虽然在BS算法的基础上，将二叉树改进为四叉树来进行识别，但是同样需要返回根节点重新进行寻呼，这样与本文的算法相比就大大增加了查询的次数和查询时间。

（2）减少了数据冗余

在标签的识别过程中，按本文算法规则对标签进行分组，阅读器收到译码后比特并得到n个冲突位，只需发送代表冲突位的指令即可进行识别，例如：阅读器收到的信息为101000XX10XX，则只需发送Request（A2，3）即可，并不需要重新发送前面的比特序列。而BS算法和4-ary QT算法中，阅读器和电子标签每次发出的寻呼是整个序列号，含有的冗余信息太大，BC-SBT算法就是在此基础上继续减除寻呼中信息冗余位，以减少传输时延和能耗。

（3）提高了识别效率和系统吞吐量

由于Aloha算法在RFID的防碰撞过程中有着很好的效果，使其广泛地被引入到标签的防碰撞的应用中，但是当标签数稍多时，该算法的效率很低，如果将信道划分为固定时隙，使得标签只能在某一时隙内应答，可将系统的效率提高1倍。本文根据该优点，在树型算法中引入了时隙的思想，使标签分时隙对阅读器进行应答，以图3所示为例：假如阅读器收到的碰撞信息为XX0XXXXXXXXXXXXX，则根据转码特点，可判断出前4位可能为“1000，0100或0001”，令所有以“1000”开始的ID在第1个时隙进行响应，以“0100，0001”开始的在第2个时隙响应。和BS算法和4-ary QT算法相比，这样即可有效地减少重复循环所发送的比特数，从而提高识别效率，大大增加了系统的吞吐率。

图3 时隙响应示例图

3.1.2 算法约定

根据标签碰撞位个数分为如下不同的形式：

（1）如果阅读器收到的编码中只有1个碰撞位，则根据标签ID的唯一性，可以直接识别出标签ID信息，并且可以判断出只有2个标签响应。

（2）如果阅读器收到的编码中有2位发生碰撞，按照本文中转码规则进行转换。例如：当阅读器收到的信息为XXX0时，则可以判断出标签发送信息经过转码后变为“1000，0100，0010”，由于转换之后的4位比特中只有一个1，可直接识别出标签中转码为“1000，0100，0010”的标签，将其按照比特转码规则还原后为“00，01，10”，并且可以直接判断出标签数为3个。

（3）如果是其他的碰撞的情况，首先将所有碰撞位按照本文的转换规则进行编码转换（如果标签长度为n，则转换之后的长度为2n），在阅读器发送查询命令后，将经过转码后的ID信息发送给阅读器，从第1位碰撞位开始，转码后首位为“1”的标签在第1时隙响应，为“0”的标签在第2时隙响应，由于转码后每4位比特中有且只有1个“1”存在，所以可以按照这个特点将每4位设定为1组，分别另碰撞位为“1”，其他3位为“0”进行识别。按照以上算法规则分组后，每组的碰撞情况可以重新转化为上述的只有1位碰撞和只有2位碰撞的方式进行识别。

3.2 算法流程

本文结合了树型搜索算法和标签分时隙响应的阅读器思想，设计基于比特转码的时隙二叉树算法，使阅读器能够准确识别出碰撞位置[12]，然后对转码后的比特信息进行分组并分配时隙。采用曼彻斯特编码[13]规则，该编码约定逻辑“1”对应信号含下降沿跳变，而逻辑“0”对应信号含上升沿跳变，若无状态跳变，则视为错误被识别。标签ID序列码根据比特转换规则进行出厂设置，转换规则按照图4所示，并以n位比特为例。阅读器内置比特转换还原模块，标签内置响应时隙计数器，时隙数根据标签转换后的位数确定。

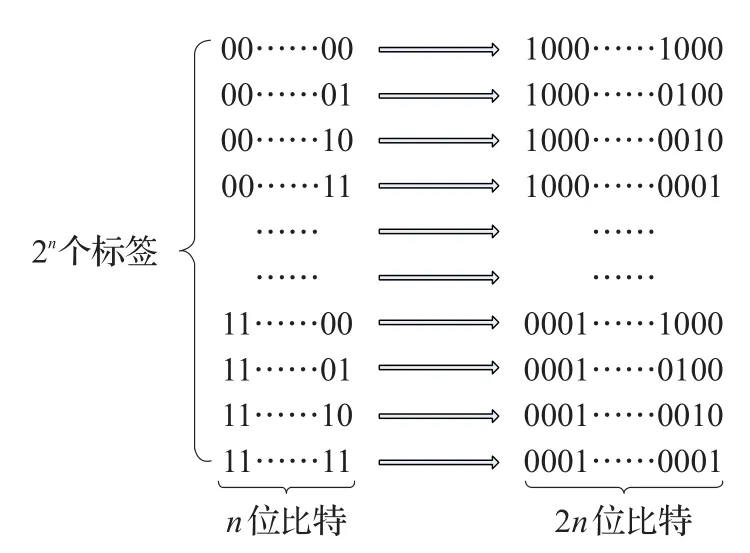
图4 n位比特一组比特转换格式示例图

（1）查询命令Request（），本文中转换规则是将每2位比特转码为4位比特，使得转换后每4位编码中有且只有1个“1”存在，基于此设置参数 Ax、Bx、Cx…（其中A，B，C…为分组序号，且 x=2，3，4）作为编码定位。例如编码转换后阅读器收到的信息为：0XXXXXX0，则可以分为A组和B组，同时另0100XXX0在第1时隙响应，0010XXX0，0001XXX0在第2时隙响应，然后阅读器发送Request（A3，1）查询命令，即可识别出符合条件的标签的ID信息。

（2）退出选择命令unselect，当标签完全被识别后，则阅读器取消对此标签的选中，使标签进入到“无声”状态。在此状态下，标签处于“非激活”状态，对于以后收到的Request命令不做回应。

BC-SBT算法流程如图5所示，步骤如下：

步骤1阅读器发送查询命令Request（）。

步骤2进行编码反向转码，经转码后所有与查询命令匹配的标签进行响应，阅读器根据曼彻斯特编码规则识别标签信息，如果没有发生碰撞，则进入到步骤4；如果发生碰撞，则进入到步骤3。

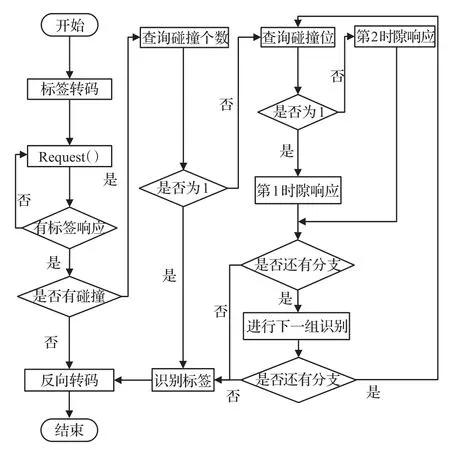
图5 BC-SBT算法流程图

步骤3判断碰撞个数和碰撞位信息，如果只有1位碰撞，根据标签ID的唯一性，可以直接识别出标签；如果有2位及以上碰撞，则根据转码规则，每4位比特中有且只有1个“1”，阅读器发送对应Request命令，使得符合条件的标签响应，最终识别后进入到步骤4。

步骤4阅读器成功识别标签后，执行unselect命令，使标签进入到“无声”状态。

3.3 算法举例

下面举例说明BC-SBT算法识别标签的步骤，假设有6个待识别标签的ID分别为a：00110010，b：10101101，c：01001010，d：11011011，e：10000110，f：01110100。经过标签内转码后变为a：1000000110000010，b：0010001 000010100，c：0100100000100010，d：0001010000100001，e：0010000101000010，f：0100000101001000。当阅读器发送查询命令后，所有标签响应阅读器，此时阅读器收到的信息为XXXXXXXXXXXXXXXX，此时共有16位发生碰撞。阅读器根据收到的信息发送查询命令，按每4位一组进行识别，首先使第1位碰撞位为“1”（同时令其他3位为“0”）的标签在第1时隙响应，阅读器发送Request（A1，1）命令，即令第一组首个碰撞位为“1”的标签进行响应，此时响应的标签只有a：1000000110000010，通过编码还原后可以直接识别出a标签。在第2个时隙中，阅读器发送request（A2，1）命令，即令第二组首个碰撞位为“1”的标签进行响应，此时，分别有c：0100100000100010，f：0100000101001000两个标签对其响应，阅读器接收的信息为0100X00X0XX0X0X0，然后将c、f标签信息压栈，继续判断碰撞位信息，同时分配下个响应时隙。在此次查询中的第1个时隙中，可以根据上述过程直接识别出标签c，进而根据算法约定规则判断出标签f，对其进行编码还原后可以识别出标签ID信息。然后，阅读器发送Request（A3，1）命令，即令第三组首个碰撞位为“1”的标签进行响应，响应的标签有两个，分别是b：0010001000010100，e：0010000101000010，此时阅读器收到的信息为001000XX0X0X0XX0，将b，e标签信息压栈，同时判断碰撞位信息，并分配响应时隙，此次查询中的第1个时隙，可以直接识别出标签b，进而识别出标签e，对其进行编码还原识别出标签ID信息。最后阅读器发送request（A4，1）命令，标签d响应，此时识别出全部标签。全部识别过程如表1所示，表中φ表示空集。

4 算法性能分析

采用叉树算法（BS）来识别n个标签时，标签之间碰撞位的位置和ID的编码值均会影响阅读器的查询次数，最好的状况下查询次数为2n-1，最坏情况下的查询次数为，通过计算，可得出BS算法完成所有标签识别的查询次数为：

表1 算法举例识别过程

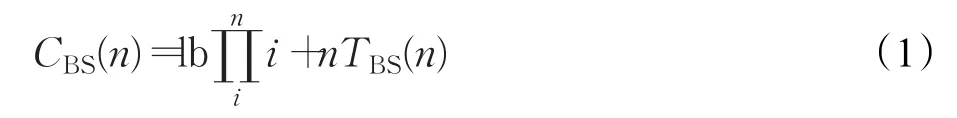
阅读器和标签的筛选过程都发送完整的序列号，若发送一次查询的时间为t，则识别n个标签的搜索时间为：

4-ary QT算法中，所有中间节点都是碰撞节点，所有的叶节点都是识别节点或空闲节点[16]，识别n个标签时，如果查询深度为L，则查询次数和查询时间分别为：

本文中BC-SBT算法中利用时隙的特点将碰撞位为“0”或“1”的标签分别在两个时隙中响应，并利用转码4位有且仅有1个“1”的规则，可以同时识别2个碰撞位，相比与BS算法在查询次数上减少了约1/2，同时对比以上两种算法，查询时间提高了至少20%，并且系统的吞吐量也明显高于BS算法和4-ary QT算法，BC-SBT算法查询次数和查询时间为：

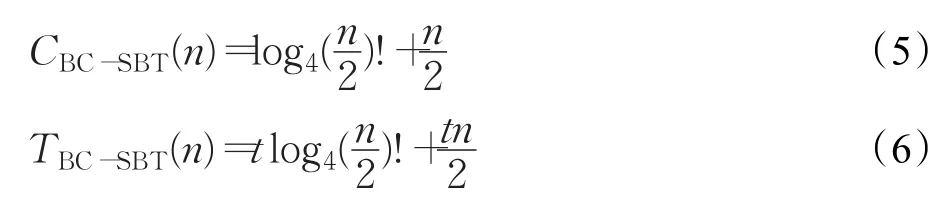
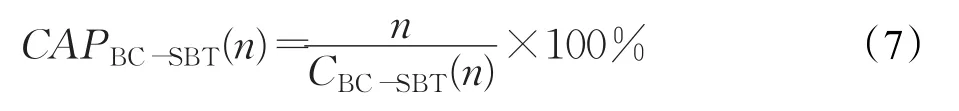
5 实验分析

为了验证改进算法的性能，本文使用Matlab进行仿真对比。实验环境为在理想信道条件下，设定标签数量n为0～1 000，标签ID识别码长度为64 bit，从阅读器的查询次数、标签的查询时间以及系统吞吐率三方面分别与文献[10]中的BS算法和文献[9]中的4-ary QT算法进行仿真比较。

图6 4-ary QT算法、BS算法、BC-SBT算法查询次数比较

大量标签的情况如图6所示，可以看出随着标签数的增加，文献[9]中的4-ary QT算法、文献[10]中的BS算法和本文中的BC-SBT算法的查询次数都在不断上升。由于BS算法是基于二叉树进行搜索，而4-ary QT算法是基于四叉树的搜索，导致查询次数上BS几乎达到4-ary QT算法的2倍；而BC-SBT算法中，由于引入转码规则，使得几乎每一次都可以直接识别出标签，与文献[9-10]进行比较，大大减少了查询次数。本文中的BC-SBT算法的查询次数上升较为缓慢，明显少于其他两种算法。基于查询次数与系统吞吐量的关系，可以反映出BC-SBT在对于系统吞吐量的优化上，要高于其他两种算法。

图7中，通过本文算法与文献[9]和文献[10]中的算法同时识别1 000个随机生成的64位标签，可以发现随着标签数量的增加，查询时间是一个呈指数上升的过程，从结果上看：当标签数小于500时，三种算法识别所用的时间差距不大；当标签数大于500时，其他两种算法所需要的时间要渐渐多余本文的BC-SBT算法；而完全识别1 000个标签时，BS算法需要大概5.4 s的时间，4-ary QT算法需要4.8 s的时间，而BC-SBT算法只用了4 s的时间，在识别效率上较其他两种算法提高了20%以上。

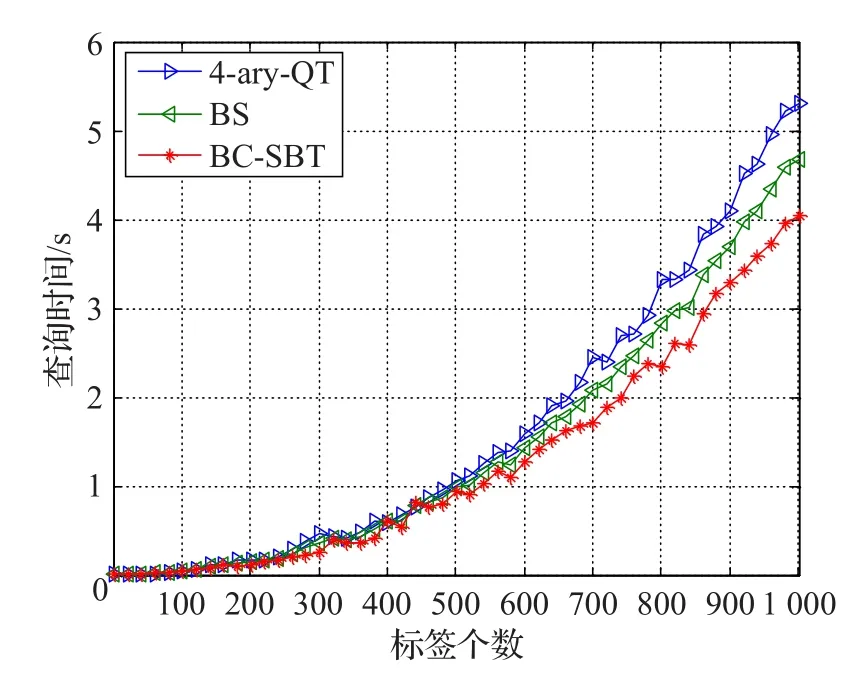
图7 4-ary QT算法、BS算法、BC-SBT算法查询时间比较

系统的吞吐率是衡量算法性能的重要指标，从图8中可以看出三种算法的吞吐率在标签超过一定数量时都呈现下降趋势，这种趋势由最初的急剧下降，到趋于平缓，这主要是因为随着标签数的增加，查询的次数也会越来越多[18-19]，但是由于文中BC-SBT算法采用时隙与转码相结合的方式，大大减少了查询次数，基于系统吞吐量的计算公式（7），可以计算出系统的吞吐量要明显优于4-ary QT算法和BS算法。

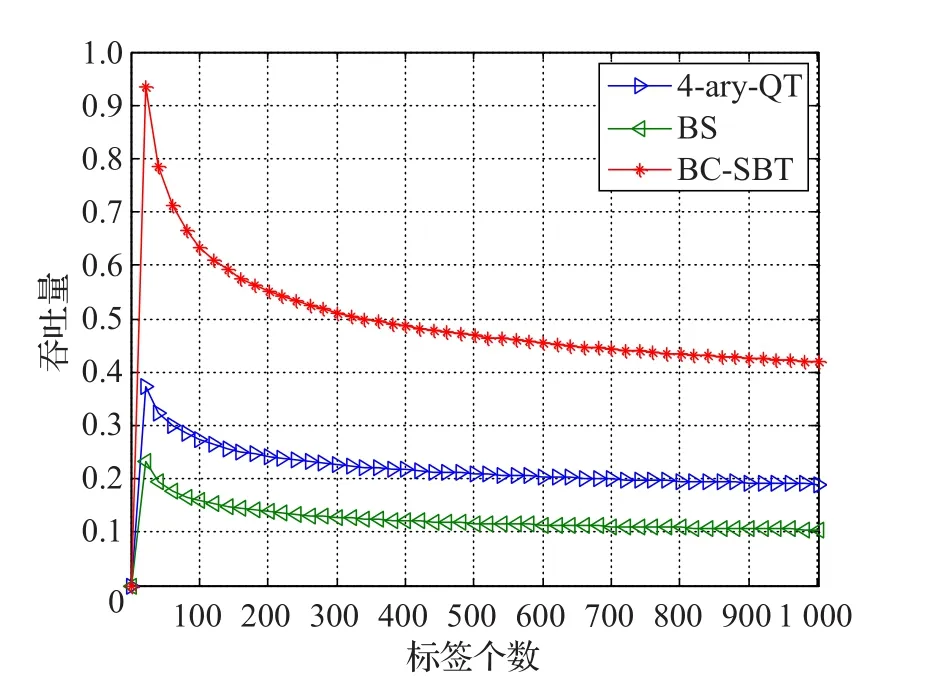
图8 4-ary QT算法、BS算法、BC-SBT算法吞吐率比较

6 结论

本文对目前研究的确定性标签防碰撞算法进行分析和比较，提出了基于比特转换的时隙二叉树RFID标签防碰撞算法，通过将标签的ID信息进行转码变换，再根据碰撞位首位的不同分时隙响应阅读器请求。经过理论分析和实验证明，本文提出的BC-SBT算法可以大大减少识别过程中所需的查询次数、查询时间和数据冗余量，同时在识别效率和系统吞吐率等方面明显优于其他防碰撞算法。随着大数据时代的来临，标签无论是数量上，还是ID识别码的长度上都会呈不断的增长趋势，本文中的BC-SBT算法在大量标签的防碰撞过程中有着更大的优势。

参考文献：

[1]宋建华，郭亚军，韩兰胜.自调整混合树RFID多标签防碰撞算法[J].电子学报，2014，42（4）：685-689.

[2]叶宁，王忠勤，王汝传.基于EPC网络的智能物资管理系统应用研究[J].计算机技术与发展，2012，22（10）：209-212.

相对于客观性、可靠性、真实性的历史成本计量模式，公允价值在现行会计制度中存在着很大的不确定性、主观性和变动性。这些因素导致的计量成果不准确，是公允价值面临的最大挑战。

[3]李平，孙利民，吴佳英.基于可离散处理的RFID防碰撞混杂算法研究[J].通信学报，2013，34（8）：10-17.

[4]李萌，钱志鸿.基于时隙预测的RFID防碰撞ALOHA算法[J].通信学报，2011，32（12）：43-50.

[5]单建锋，陈明，谢建兵.基于ALOHA算法的RFID防碰撞技术研究[J].南京邮电大学学报，2013，33（1）：56-61.

[6]吴海峰，曾玉.自适应帧Aloha的RFID标签防冲突协议[J].计算机研究与发展，2011，48（5）：802-810.

[7]丁治国，郭立，朱学永.基于二叉树分解的自适应防碰撞算法[J].电子与信息学报，2009，31（6）：1395-1398.

[8]张学军，王娟，王锁萍.基于标签识别码分组的连续识别防碰撞算法研究[J].电子与信息学报，2011，33（5）：1159-1165.

[9]Kim Y，Kim S，Ahn S L K.Improved 4-ary query tree algorithm for anti-collision in RFID system[C]//International Conference on Advanced Information Networking and Applications，2009：699-704.

[10]王雪，钱志鸿，胡正超.基于二叉树的RFID防碰撞算法的研究[J].通信学报，2010，31（6）：49-57.

[11]张学军，马军飞，鲁友.基于位编码单元的双时隙防碰撞算法[J].计算机技术与发展，2014，24（9）：93-102.

[12]王必胜，张其善.可并行识别的超高频RFID系统防碰撞性能研究[J].通信学报，2009，30（6）：108-113.

[13]梁彪，胡爱群，秦中元.一种新的RFID防碰撞算法设计[J].电子与信息学报，2007，29（9）：2158-2160.

[14]Cheng T，Jin L.Analysis and simulation of RFID anticollison algorithm[C]//IEEE Advanced Communication Technology，2007：697-701.

[15]Eom J B，Lee T J.Accurate tag estimation for dynamic framed-slotted ALOHA in RFID systems[J].IEEE Comumunication Letters，2010，14（1）：60-62.

[16]Zhang Xuejun，Ye Chuanling，Ma Junfei.An improved anti-collision algorithm with intelligent seperation for RFID system[J].International Journal of Advancements in Computing Technology，2012，4（22）：823-831.

[17]Tian Yun，Chen Gongliang，Li Jianhua.Bi-slotted binary tree algorithm with stack for radio frequency identification tag anti-collision[J].Shanghai Jiao Tong University，2013，18（2）：173-179.

[18]Lai Y C，Hsiao L Y.Optimal slot assignment for binary tracking tree Protocol in RFID tag identification[J].IEEE/ACM Transactions on Networking，2015，23（1）.

[19] Šlic P，Radić J，Rožć N.Energy efficient tag estimation method for ALOHA-based RFID systems[J].IEEE Sensors Journal，2014，14（10）：3637-3647.