基于图分析的OFDM频谱感知

白 玉，闫 坤，李少鹏，张华伟，刘 毅

BAI Yu,YAN Kun,LI Shaopeng,ZHANG Huawei,LIU Yi

桂林电子科技大学 信息与通信学院，广西 桂林 541004

School of Information and Communication,Guilin University of Electronic Technology,Guilin,Guangxi 541004,China

1 引言

为缓解日益紧张的频谱资源匮乏的问题，1999年，Joseph Mitola博士提出了认知无线电（Cognitive Radio，CR）的概念[1-2]，认知无线电是一种提高频谱资源利用率的智能新技术，频谱感知是认知无线电的前提和关键技术之一[3]，首先利用信号检测技术感知频谱空洞，提高频谱资源利用率；其次，检测授权用户的出现，避免干扰授权用户通信[4]，信号检测是频谱感知技术的基础。

目前常用的频谱感知方法主要有匹配滤波器检测[5]、能量检测[6-7]、循环平稳特征检测[8-9]等。匹配滤波器检测通过对授权信号进行相干解调或导频检测来判断授权用户是否存在[10]。匹配滤波器检测虽然能获得较高的处理增益，但需要授权用户的先验信息，而且要求定时和频率同步[11]；能量检测是一种非相关检测算法，通过对一段检测空间（时域或频域）内的接收信号总能量进行测量，并与预先设定的能量阈值进行比较，以此为依据判断授权用户是否存在。能量检测方法实现简单，灵活性强，计算复杂度低，对授权用户先验信息无任何要求，但鲁棒性较差，容易受到噪声影响[12]；循环平稳特征检测通过检测接收信号是否具有循环平稳特性来判断授权用户是否存在[13]。循环平稳特征检测无需授权用户的先验信息仍然具有良好的检测性能，但是计算复杂度高，实时性差。三种检测方法各有优劣，其中能量检测法是目前最常用的频谱感知方法。

文献[14-15]提出了一种基于图（Graph）的离散信号表示与处理框架（Discrete Signal Processing on Graphs，DSPG），文中采用图的形式表示信号，用图的顶点表示信号的采样点，（加权）图的边表示采样点之间的相关性。这种基于图的离散信号处理理论扩展了传统离散信号处理理论，并已得到多项应用。文献[16]提出了一种基于图的信号采样理论，文献[17]提出了一种基于图的信号去噪技术，文献[18]提出了一种基于图的信号分类技术。

本文在文献[14-15]基础上，提出了一种基于图的OFDM信号频谱感知方法。首先，将信号或信号的功率谱用加权图（weighted graph）的形式来表示，这种新的表示形式虽然会丢失信号的部分相位信息，但是仍保留了大量的幅度信息及统计信息。通过分析图的顶点及连通性信息，引入了加权图的邻接矩阵进行信号检测。本文采用邻接矩阵部分元素和作为检测统计量，并将其与预先设定的判决门限进行比较，以此判断OFDM信号是否存在。这种基于图分析的OFDM感知方法，实现简单，计算复杂度低，无需接收信号的任何先验信息，而且，在低信噪比下，仍具有良好的检测性能。

本文主要分为5章。第1章引言中阐述了本文的研究背景，以及目前常用的频谱感知技术，并对本文内容作了简单概述。第2章给出了OFDM信号模型。第3章重点研究了本文所提出的基于图分析的OFDM频谱感知方法，详细分析了检测原理以及判决门限的设定。第4章通过仿真实验，验证了所提方法的可行性，并对其检测性能进行了分析。第5章对本文进行了总结，指出了需要进一步开展研究的工作。

2 OFDM系统模型

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）传输系统具有高传输速率，高频谱利用率和抗多径干扰能力强等优点，并能够灵活地进行频谱选择，因此成为现代无线通信调制方式的最佳选择[19-20]。

OFDM信号模型如下：

其中，K表示子载波数目，Ckl表示第l个符号的第k个子载波上调制的信号，它通常取自一个固定的星座集；fc表示载波频率；Δf表示子载波间隔，一般取Δf=1/Tu；完整符号周期Ts=Tu+Tg，Tu表示有用符号时长，Tg表示循环前缀时长；g(t)为发送滤波器脉冲响应函数。

3 基于图分析的频谱感知

频谱感知过程可以用一个二元检测模型来表示：

其中，n=1,2,…,N，N为采样点数，w(n)表示均值为0，方差为的加性高斯白噪声，s(n)表示OFDM信号，s(n)和w(n)相互独立，x(n)为接收信号。频谱感知就是区分H0和H1两种假设的过程。

本文所提出的基于图分析的OFDM频谱感知方法检测流程如图1所示。首先，采用周期图法估计接收信号x(n)的功率谱，如果x(n)中存在OFDM信号，其功率谱会含有冲激分量，若对功率谱做最大值归一化处理，由于冲激分量的存在，大部分采样点的归一化后的值会变得较小；接着，选取合适的量化级数，对归一化后的功率谱进行均匀量化。相应的，量化后的大部分采样点的功率谱值分布在较低的量化级上。如果x(n)中不存在OFDM信号，其量化后功率谱值近似均匀地分布在各个量化级上。接收信号功率谱的这一特性，会在其邻接矩阵（边权矩阵）中表现出来，本文采用邻接矩阵部分元素和作为检测统计量，具体检测过程如下文所述。

图1 检测流程图

一个图G=(V,E)可由两个集合来定义：一个有限集合V={v1,v2,…,vM}，它的元素称为顶点；另一个集合E，它的元素是一对顶点，称为边。本文将信号的功率谱采用加权图的形式来表示，加权图是一种给边赋了值的图，这些值称为边的权重（weight）或成本（cost）。首先对信号功率谱作最大值归一化，则归一化后的功率谱取值范围为[0,1]；然后采用均匀量化，设量化间隔为，则量化值分别为1,2,…,M，本文以量化级1,2,…,M作为图的顶点集V{vi=i|i=1,2,…,M}，相邻采样点功率谱之间的连线作为图的边集E，即，若第k个采样点的量化值为i，第k+1个采样点的量化值为 j，则称边集E中存在边。在计算机算法中，图的表示有两种方法：邻接矩阵或邻接链表，本文采用邻接矩阵的形式来表示图。M个顶点的邻接矩阵是一个M×M的矩阵，图中的每个顶点都由一行和一列来表示，加权图的邻接矩阵也称权重矩阵，当存在一条从第i个顶点到第 j个顶点的边时，邻接矩阵元素A(i,j)即为权重Wij，若边不存在，令A(i,j)等于0：

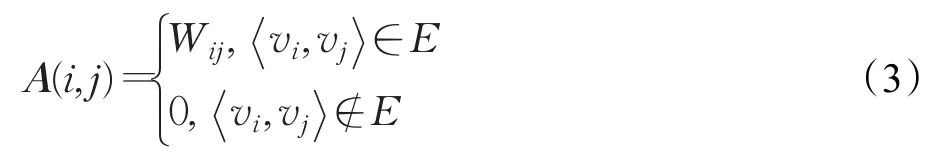
其中，权重Wij定义为边的重量，即边的数目。邻接矩阵不仅能反映当前采样点的量化情况，而且能反映相邻采样点的量化情况。若接收信号中存在OFDM信号，则其大部分采样点分布在较低的量化级上，这一特性可以用邻接矩阵左上角元素和来体现。综上所述，可以在邻接矩阵左上角选取一个m×m(1≤m＜M)的子矩阵，以该子矩阵的元素和作为检测统计量T，设TH0表示H0下的检测统计量，TH1表示H1下的检测统计量，则有：

其中，TH0可以通过公式计算出来，详细的计算过程如下文所述。因此，本文定义判决门限γ：

其中，K是大于1的常数，通过设不同的K值，来设定不同的判决门限。如果T＞γ，判决H1成立，即OFDM信号存在；反之，则判决H0成立，即OFDM信号不存在。

下面确定判决门限γ：

在H0的状态下，OFDM信号不存在，接收信号x(n)是纯噪声：

首先，采用周期图法估计接收信号的功率谱：

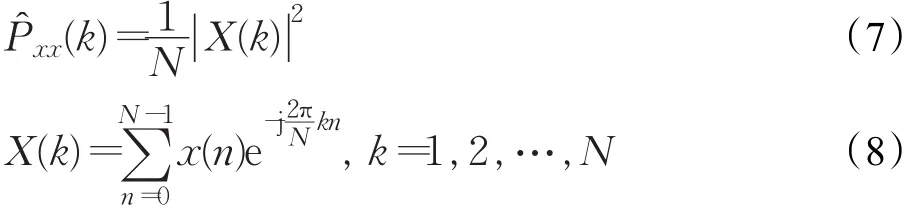
X(k)实部和虚部均服从均值为0，方差为的高斯分布[21]，即：

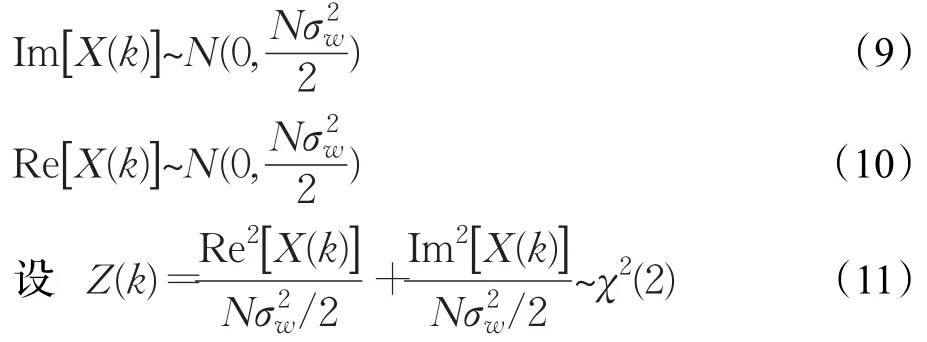
所以，Z(k)服从自由度为2的χ2分布，也即参数为2的指数分布。则功率谱(k)服从参数为的指数分布。

其次，以功率谱的最大值对信号功率谱进行归一化处理。设功率谱最大值为Pmax，以对信号功率谱进行归一化处理：

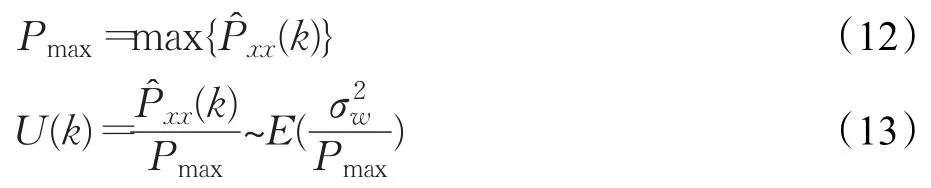
U(k)服从参数为的指数分布，其累积概率分布函数为：

第三，对归一化后的功率谱做均匀量化，设量化阶数为M，不同的量化阶数，检测性能也会有所不同。在均匀量化时，量化间隔为：

若U(k)=0，令量化后的U(k)=1；

其中，i=1,2,…,M 。

最后，求量化后的功率谱图的邻接矩阵A。以量化级1,2,…,M 作为图的顶点集V{vi=i|i=1,2,…,M}，相邻采样点功率谱之间的连线作为图的边集E，邻接矩阵元素Aij等于边的数目。N个采样点之间共有N-1条边，所以，邻接矩阵A的所有元素之和为N-1。在邻接矩阵左上角选取一个子矩阵，以该子矩阵的元素和作为检测统计量T。m的取值与M正相关，设：

称sr为检测统计量系数，sr取值不同，系统的检测性能也会有所不同。

由公式（13）可知归一化后的功率谱概率分布，则功率谱量化值小于等于m的概率为：

对噪声而言，可以假设相邻采样点的功率谱独立同分布，所以，相邻采样点的量化值都小于等于m的概率为：

又由公式（5）可知，判决门限γ可以设为：

式中，判决系数K是大于1的常数，通过不同的K值，来设定不同的判决门限，经过大量的仿真实验发现：1.09≤K≤1.1时，检测性能最好。

4 仿真验证

OFDM系统和许多数字通信系统一样，以帧的形式将被发送的信号组织在一起。本文仿真所用的结构是802.11 g标准。仿真所用OFDM信号包含20个符号帧，每帧由100个OFDM符号组成，数据时长为9.6 ms，具体参数如表1所示。

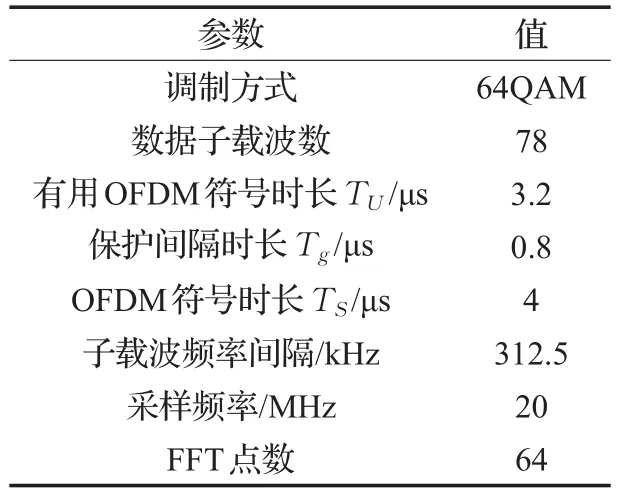
表1 OFDM系统参数

为了检验这种基于图分析的OFDM频谱感知方法的性能，本文在MATLAB环境下，采用蒙特卡洛方法构建仿真模型，分别进行了以下仿真分析。设蒙特卡洛次数Ns=1 000次，量化级数M=20。

首先对传统能量检测和本文提出的基于图分析的OFDM信号检测方法进行比较，图2给出了相同信噪比下两种检测方法的ROC曲线。其中信噪比分别为-14dB、-15dB，sr=0.2，从图中可以看出，基于图分析的OFDM信号检测法相较于传统能量检测，其性能更优越。当信噪比为-15dB，虚警概率Pf=0.1时，检测概率Pd约等于0.92，而当虚警概率Pf≥0.6时，检测概率Pd趋近于1。

图2 相同信噪比下传统能量检测法和基于图分析的OFDM信号检测法检测性能比较（K=1∶0.001∶1.1）

图3 为不同信噪比下基于图分析的OFDM信号检测法的性能仿真对比，其中，sr=0.2，信噪比分别为-14dB、-15dB、-16dB、-17dB、-18dB，比较图中曲线可以看出，信噪比大于等于-16dB时具有良好的检测性能，若信噪比低于-16dB容易导致漏检，从而检测概率下降，系统性能也随之降低。在低信噪比下可以通过增加检测时长来提高检测概率，本文仿真所用数据时长为9.6 ms。

图3 不同信噪比下基于图分析的OFDM信号检测法检测性能比较（K=1∶0.001∶1.1）

检测统计量T系数取值不同，系统的检测性能也会有所不同，图4所示为信噪比SNR=-15dB时，sr取值对检测性能的影响，由图4可以看出，随着sr的增加，系统检测性能有所下降，这是由于sr越大检测统计量T也越大，TH0和TH1之间的差值也越小，检测性能也随之降低。应该注意到sr取值也不能任意取值，因为m=sr×M，m为所取子矩阵的大小，必须是一个正整数。

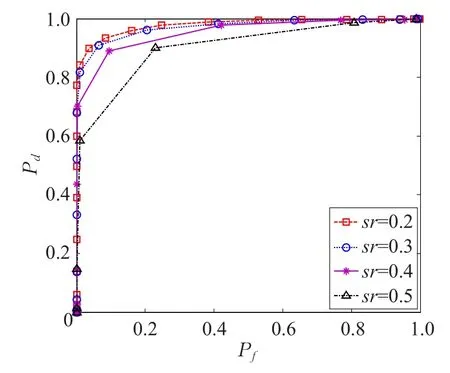
图4 sr的取值对检测性能的影响（K=1∶0.001∶1.1）

5 总结

本文采用了一种新的方法，将信号的功率谱用图的形式来表示，提出了一种基于图分析的OFDM频谱感知方法，引入了图中邻接矩阵的概念，用邻接矩阵部分元素和作为检测统计量，通过与预先设定的判决门限作对比，以此判决OFDM信号是否存在。这种方法，实现简单，计算复杂度低，无需接收信号的任何先验信息，在低信噪比下，仍具有良好的检测效果，但噪声不确定性对其性能会有一定的影响，因此后续研究的工作，会围绕噪声不确定性展开，以期可以降低噪声不确定性对检测性能的影响。

参考文献：

[1]Mitola J，Maguire G Q.Cognitive radio：Making software radios more personal[J].IEEE Personal Communications，1999，6（4）：13-18.

[2]Mitola J.Cognitive radio for flexible mobile multimedia communications[C]//IEEE International Workshop on Mobile Multimedia Communications，San Diego，CA，1999：3-10.

[3]Li Zhen，Zhu Geqing，Wang Weihua，et al.Improved algorithm of multiuser dynamic subcarrier allocation in OFDM system[C]//Proceedings International Conference on Communication Technology.Beijing，China：Beijing University of Posts and Telecommunication Press，2003：259-268.

[4]Bansal G，Hossain M J，Bhargava V K.Adaptive power loading for OFDM-based cognitive radio systems with statistical interference constraint[J].IEEE Transactions on Wireless Communications，2011，10（9）：2786-2791.

[5]Sun H，Nallanathan A，Wang C X，et al.Wideband spectrum sensing for cognitive radio networks：A survey[J].IEEE Wireless Communications，2013，20（2）：74-81.

[6]Liang Y C，Chen K C，Li G Y，et al.Cognitive radio networking and communications：An overview[J].IEEE Transactions on Vehicular Technology，2011，60（7）：3386-3407.

[7]赵小龙，赵杭生，曹龙，等.基于改进型能量检测的加权协作频谱感知算法[J].计算机工程与应用，2013，49（24）：61-64.

[8]王尚，汪一鸣，欧扬.基于循环平稳的图样特征识别频谱检测方法[J].计算机工程与应用，2013，49（11）：153-157.

[9]杨威.基于信噪比权值的累量循环平稳检测协作感知[J].电子测量技术，2012，35（1）：46-49.

[10]Cabric D，Mishra S M，Brodersen R W.Implementation issues in spectrum sensing for cognitive radios[C]//Conference Record of the Thirty-Eighth Asilomar Conference on Signals，Systems and Computers，2004：772-776.

[11]陈国忠.基于认知无线电的频谱感知技术研究[D].南京：南京邮电大学，2012.

[12]Leshem A，Zehavi E，Yaffe Y.Multichannel opportunistic carrier sensing for stable channel access control in cognitive radio systems[J].IEEE Journal on Selected Areas in Communications，2012，30（1）：82-95.

[13]刘春红.基于OFDM的认知无线电系统中的功率分配机制研究[D].哈尔滨：哈尔滨工业大学，2011.

[14]Chen S，Varma R，Sandryhaila A，et al.Discrete signal processing on graphs：Sampling theory[J].IEEE Transactions on Signal Processing，2015，63（24）：6510-6523.

[15]Sandryhaila A，Moura J M F.Discrete signal processing on graphs：Frequency analysis[J].IEEE Transactions on Signal Processing，2014，62（12）：3042-3054.

[16]Narang S K，Gadde A，Ortega A.Signal processing techniques for interpolation in graph structured data[C]//2013 IEEE InternationalConference on Acoustics，Speech and Signal Processing，Vancouver，2013：5445-5449.

[17]Chen S，Sandryhaila A，Moura J M F，et al.Signal denoising on graphs via graph filtering[C]//2014 IEEE Global Conference on Signal and Information Processing（GlobalSIP），Atlanta，GA，2014：872-876.

[18]Chen S，Cerda F，Rizzo P，et al.Semi-supervised multiresolution classification using adaptive graph filtering with application to indirect bridge structural health monitoring[J].IEEE Transactions on Signal Processing，2014，62（11）：2879-2893.

[19]Mahmoud H A，Yucek T，Arslan H.OFDM for cognitive radio：Merits and challenges[J].IEEE Wireless Communications，2009，16（2）：6-15.

[20]Budiarjo I，Nikookar H，Ligthart L P.Cognitive radio modulation techniques[J].IEEE Signal Processing Magazine，2008，25（6）：24-34.

[21]Yucek T，Arslan H.A survey of spectrum sensing algorithms for cognitive radio applications[J].IEEE Communications Surveys&Tutorials，2009，11（1）：116-130.