基于目标跟踪的自适应广义高阶CKF算法

彭志颖，夏海宝，许蕴山

PENG Zhiying,XIAHaibao,XU Yunshan

空军工程大学 航空航天工程学院，西安 710038

College ofAeronautics andAstronautics Engineering,Air Force Engineering University,Xi’an 710038,China

1 引言

非线性滤波源自含噪声观测值的非线性随机系统的状态估计问题，围绕Arasaratnam等[1]提出的非线性高斯滤波框架，发展出了一系列次优非线性滤波方法[2]，如文献[3-7]中提出的扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）、中心差分卡尔曼滤波（CDKF）等非线性滤波算法，其中Jia等提出的高阶容积卡尔曼滤波算法（CKF）[8]及其高阶形式凭借良好的滤波性能而得到广泛应用。然而，当系统存在模型不确定性或状态突变时，CKF算法中的增益矩阵对预测残差突变反应滞后，导致状态估计精度急剧下降。

强跟踪滤波（STF）基于正交理论，通过自适应渐消因子(λk)实时调整增益矩阵，具有较强的鲁棒性和应对状态突变等不确定因素的能力。文献[9]针对模型不确定时CKF精度下降问题，将STF和CKF相结合，提出自适应容积卡尔曼滤波（ACKF）算法。文献[10]针对STF的理论局限以及基于UT变换的强跟踪滤波器（UTSTF）处理高维非线性系统时滤波精度下降甚至发散等问题，提出一种基于CKF的强跟踪滤波器（CKFSTF）。文献[9-10]中的强跟踪算法具有一定的自适应滤波能力，但是所提算法仍然采用三阶球面-径向容积规则，其滤波精度只能达到泰勒级数展开的三阶项，尤其对于强非线性系统，基于此种容积准则的CKF算法估计精度有限[11]。文献[11]基于任意阶的全对称球面插值准则和矩匹配原理提出了一种自适应高阶容积卡尔曼滤波（AHCKF）算法，在带有状态突变的机动目标跟踪中获得良好的估计效果，但构造方式复杂，不易向高阶扩展，协方差矩阵易失去正定性，出现滤波中断的现象。

为解决上述问题，本文提出一种自适应广义高阶容积卡尔曼滤波（AGHCKF）方法。首先给出广义高阶容积准则[12]，证明其相对三阶容积准则具有更高的估计精度，与高阶容积准则相比具有相近的估计精度，但扩展性更好的特点；将广义高阶容积卡尔曼滤波算法（GHCKF）与非线性STF相结合，并采用矩阵对角化变换代替传统的乔勒斯（Cholesky）分解进行协方差矩阵的分解，提出AGHCKF方法，并给出其具体算法流程。最后将提出的算法应用于带有未知状态突变的机动目标跟踪问题并进行数值仿真，仿真实验表明了所提算法的有效性和可行性。

2 容积准则

2.1 容积卡尔曼滤波

考虑如下形式的离散非线性系统：

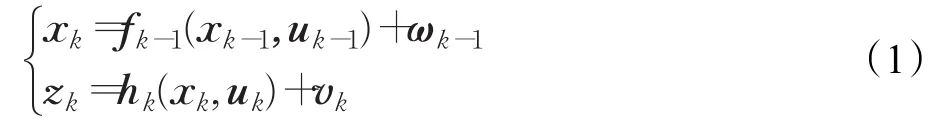
其中，xk∈ℝnx和zk∈ℝnz分别为系统状态向量和量测向量；f(·)和h(·)为已知的非线性函数；ωk-1和vk为独立的零均值系统状态高斯白噪声和系统量测高斯白噪声，分别满足，其中δkl是Kronecker-δ函数；初始状态 x0与ωk和vk不相关；uk∈ℝnu为控制输入向量。

非线性滤波难点在于求解形如：

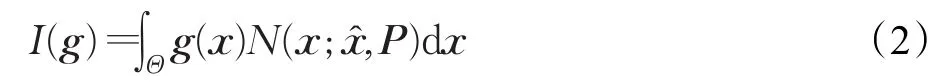
的非线性函数与高斯概率密度函数的数值积分问题。其中，Θ∈ℝn表示积分区域，x为状态变量x的估计值，P为x的方差。文献[1]将贝叶斯估计理论与球面-径向容积准则相结合，推导出CKF方法，得到三阶球面-径向容积准则：

其中，n表示应用对象的阶数，表示容积点，ωi=1/(2n)为容积点的权值，[1]i∈ℝn表示完全对称点集[1]的第i个元素。

传统CKF中正的容积点权值会导致估计点越界或者产生形式复杂的估计点[13]；当n足够大时，容积点ξi可能超出积分区域，另外，将球面-径向积分进行高阶拓展需同时提升容积准则和高斯-拉盖尔准则的阶数，并计算n维超球体的面积分，计算过程复杂，导致CKF算法的高阶扩展性较差。

2.2 广义容积准则

考虑实数域ℝn上积分：

对式（4）进行计算，选取前两条G-轨迹[14]，构成如下完全对称形式的积分公式。

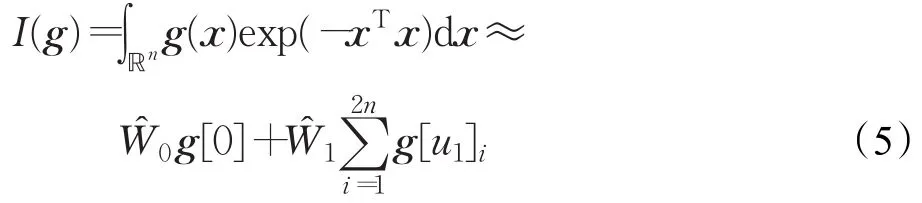
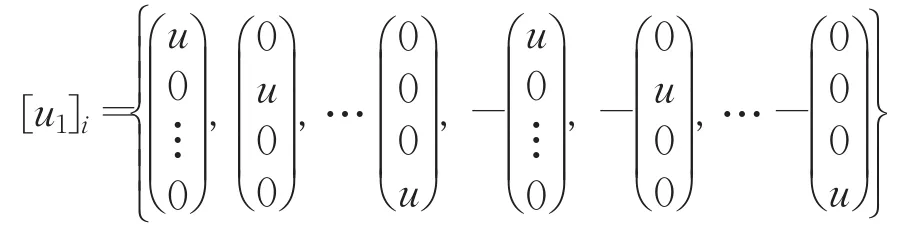
其中，和是相对于 G-轨迹[0]和 [u1]的权值，n为系统状态维数。其中[u1]i具有如下形式：

考虑g在集合{1,}上的积分值，可得：

其中：

由于u1、W0和W1为未知量，式（6）为欠定方程组，有无穷多组解。当取时，得到，状态噪声和量测噪声均值为零，将积分变换至标准高斯分布：

其中，0和I分别为零矩阵和单位矩阵，容积点，权值ωi=1/(2n)，且 i=1,2,…,2n，n为系统状态的维数。该结论与三阶球面-径向容积准则推导的结果完全一致。

可以看到，通过选取不同u1值，可构造出无穷多包含(2n+1)个点的CKF算法，但仅由2n个容积点组成的CKF是唯一存在的，且形式上与三阶球面-径向容积准则结果完全一致。可见，传统的容积准则实际是广义容积准则的一个特例。

2.3 广义高阶容积准则

为构造GHCKF，分别选取第一、第二及第三G-轨迹，构成如下广义五阶容积积分公式[14]：

其中是 G-轨迹[u1,u1]的权值。利用式（10）计算{1,,,|i≠j}的积分。

其中，I0和 I2分别由式（7）和式（8）给出。 I4和 I2,2为：

方程组（11）中，仅有 u1、、和四个未知，求解可得唯一解：

将式（10）变换至标准高斯分布，可得：

其中容积点和权值分别为：

将式（15）～式（17）置于卡尔曼滤波框架下，即可得到标准GHCKF算法。具体算法流程参考文献[14]，限于篇幅，在此不再赘述。下面给出三阶球面-径向容积准则和广义高阶容积准则的逼近误差分析。

（1）若函数g(x)无法被精确到三阶的多项式拟合时，会产生逼近误差，误差主要来源于四阶项，其中i,j=1,2,…,n，且d=0,1,…,n。不失一般性，考虑四阶项（其中 i≠1），则球面-径向容积准则的估计误差为：

形如的四阶项，因其含有坐标变量的奇次项，故积分为零。则x1-轴的总逼近误差可表示为：

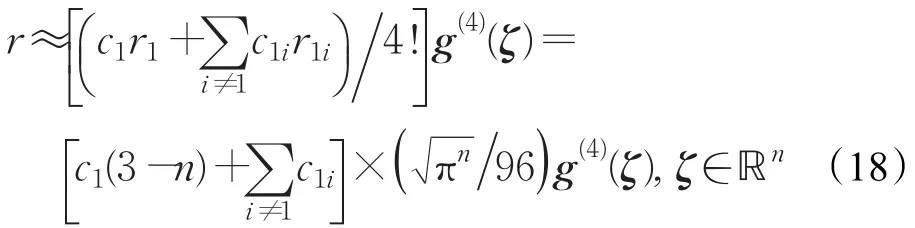
其中，c1为四阶项的系数，c1ir1i是互误差项在x1-轴的投影。

（2）广义高阶容积准则主要误差来源于六阶项,i,j=1,2,…,n;d=0,1,…,6。不失一般性，考虑六阶项和，相应的得出x1-轴的逼近误差为：

其中，为单项式的系数，和分别是互误差项及的积分在x1-坐标轴的投影。

与式（18）相比，式（19）的逼近误差的分母要大得多，且误差不随状态空间的维数增长而增长。因此，基于广义五阶容积准则的GHCKF比基于传统球面-径向容积准则的CKF估计精度更高。通过选取更高阶的G-轨迹，可构造出任意阶的广义高阶容积滤波算法，具有良好的高阶扩展性。

对文献[8]中的高阶容积准则和本文中的广义高阶容积准则进行分析。二维情况下两种容积准则在第一象限的Sigma点如图1所示。

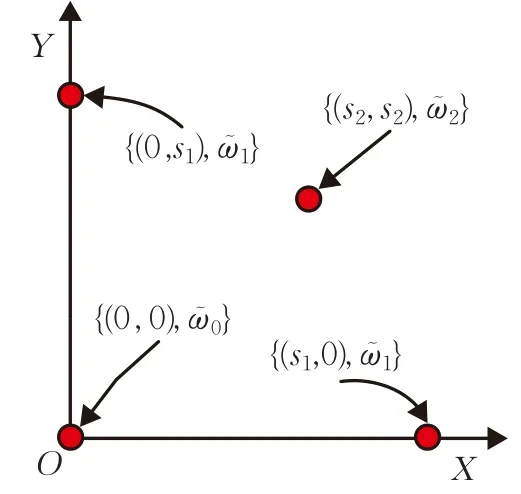
图1 二维情况下高阶容积变换在第一象限的Sigma点

将图1中二维情况推广到n维空间，可以看出两种准则都需要三类Sigma点：第一类Sigma点位于坐标原点，点数为1；第二类Sigma点对称地分布在与原点距离相同的n条坐标轴上，点数为2n；第三类Sigma点对称地分布于(0 ,…,±s1k,…,±s1l,…)T（第 k个和第 l个元素不为0，k＜l，k,l=1,2,…,n），点数为 2n(n -1)。两者的容积点个数都为2n2+1，区别仅在于各个Sigma点的权值不同。从而两种高阶容积准则具有相近的估计精度。

3 自适应广义高阶容积卡尔曼滤波

3.1 非线性强跟踪算法

STF原理是通过在预测协方差矩阵Pk|k-1中引入一个自适应渐消因子λk，达到在线调整增益矩阵Kk的目的，滤波器需要满足2个条件：

式（20）使得滤波器满足最小方差估计的性能指标。式（21）强迫滤波器的残差序列时刻保持正交，克服了滤波器在遇到模型不确定或者状态突变等情况时，因为残差序列不正交，导致滤波器性能下降的问题[8-9]，使得强跟踪滤波器对模型不确定性有较强的鲁棒性，对状态突变有较强的跟踪能力。

非线性STF算法核心结构为：

式中，为k时刻的状态估计值；zk为k时刻的量测值，Kk为滤波增益，ek为量测残差。λk的计算方法为：

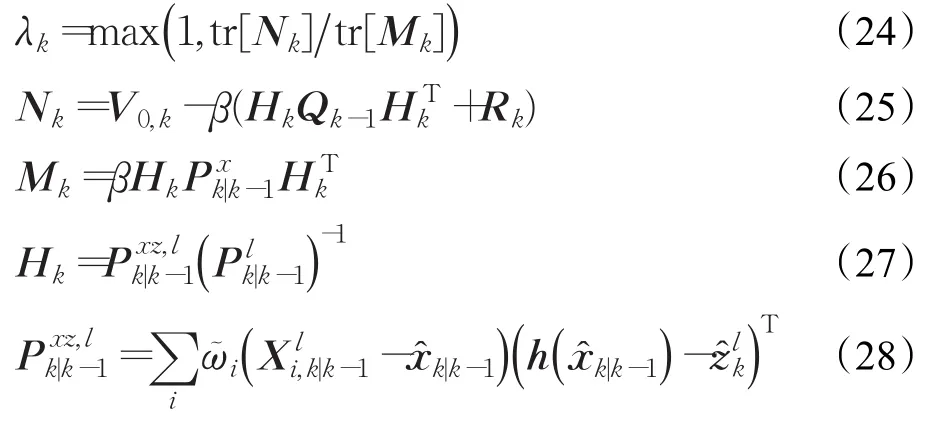
式中，和分别为不考虑和考虑λk和vk-1的状态预测误差的协方差阵，满足=+；为未考虑λk的互协方差矩阵；为积分权值，如式（16）；为不考虑λk的状态一步预测产生的容积点；是由得到的预测量测值，如式（33）～式（37）；Nk、Mk、Hk和V0,k均为计算过程参数矩阵；弱化因子β=3，ρ为遗忘因子，取ρ=0.95。

3.2 自适应广义高阶容积卡尔曼滤波

以GHCKF为框架，将STF中的λk引入到时间和测量更新方程中构造AGHCKF，如图2所示。

图2 AGHCKF算法流程图

在构造AGHCKF算法过程中，由于计算误差、舍入误差和模型失准等原因，协方差矩阵易失去正定性，导致滤波中断。考虑到协方差矩阵的平方根形式保留了协方差矩阵的特征空间信息，可使协方差传递更加准确；矩阵对角化变换不要求协方差矩阵正定，可避免协方差矩阵非正定引起的滤波中断。本文将矩阵对角化变换引入算法的时间和量测更新过程，以提高AGHCKF的滤波精度和稳定性。

假设k-1时刻的状态向量xk-1的后验概率密度函数满足，误差协方差阵的特征平方根初值。则得到AGHCKF算法如下：

（1）时间更新

①计算容积点Xi,k-1|k-1(i=1,2,…,2n)

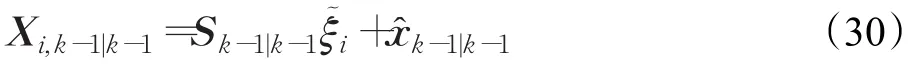
②计算由状态方程传播后的容积点

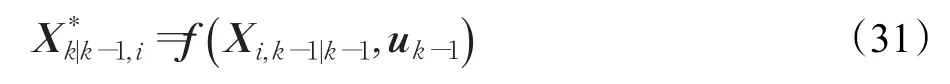
③计算当前时刻的状态估计值

④计算未引入渐消因子的预测误差协方差阵

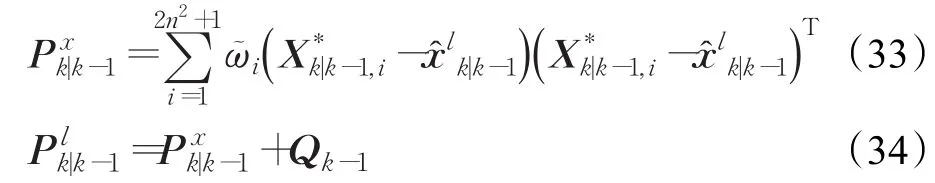
⑤计算的矩阵对角化变换

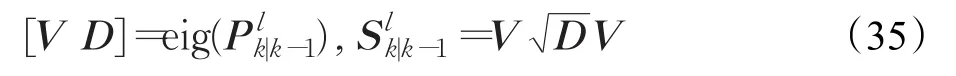
其中上标l表示未加入渐消因子。

（2）计算自适应渐消因子

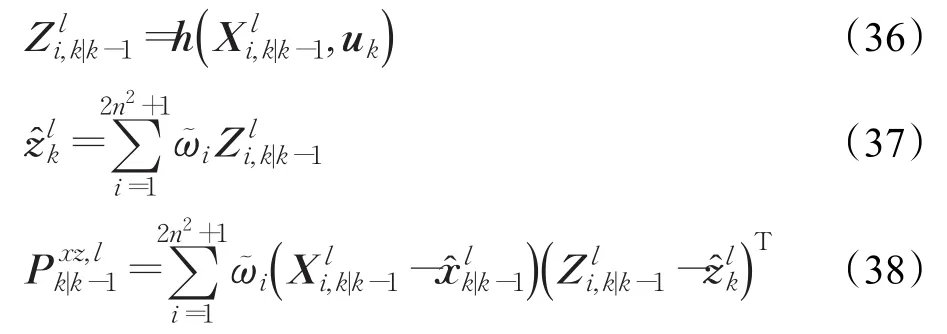
将式（34）、式（38）代入式（27）求取 Hk的等价表述，再利用式（23）～（26）、式（28）和式（29）求取自适应渐消因子λk。

①计算引入渐消因子后的协方差矩阵Pk|k-1

②计算由Pk|k-1生成的容积点

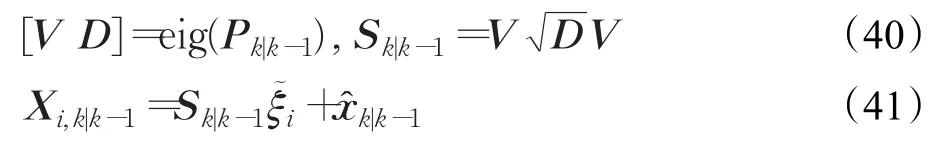
（3）量测更新

①计算k时刻的量测预测值

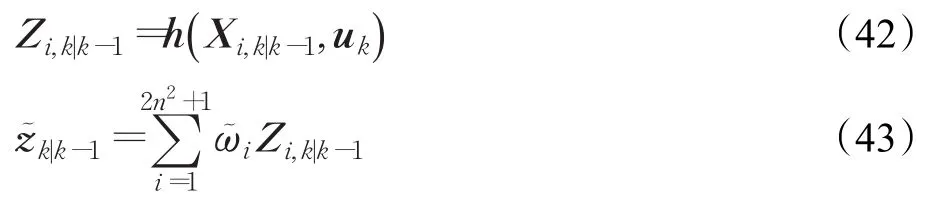
②计算k时刻引入渐消因子的量测误差协方差阵Pzz,k|k-1和引入渐消因子的预测互相关协方差阵Pxz,k|k-1。

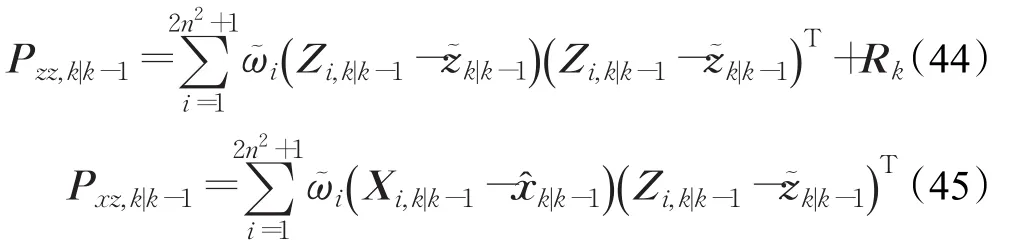
③计算滤波增益矩阵Kk

④当前时刻k的滤波状态值

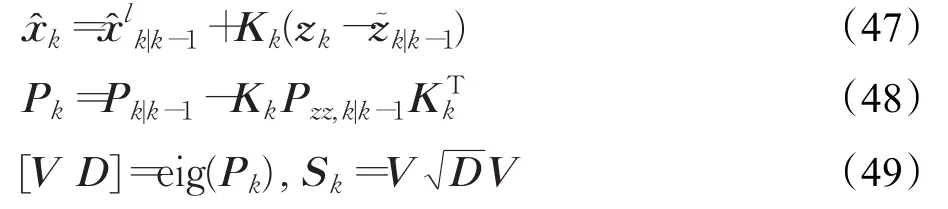
4 数值仿真

将AGHCKF算法应用到具有未知机动的目标跟踪系统中，并与CKF、GHCKF、交互式多模型-容积卡尔曼滤波器（IMM-CKF）[15]和ACKF进行对比。定义地面坐标系o-xyz的原点位于地面，ox指向东向，oy指向北向，oz指向天向。假设目标以未知角速度Ω等高度机动飞行，飞行高度h=10 000 m，目标的运动由如下模型描述：

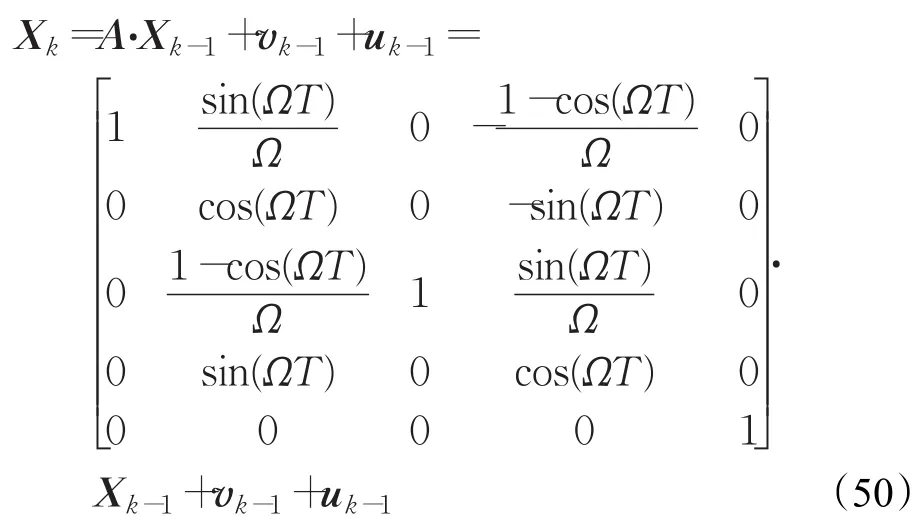
其中，为 k 时刻目标状态和为目标的位置和速度矢量；Ω为未知的目标转弯角速度；uk-1为机动输入；高斯白噪声vk-1～N(0,Qk)，协方差矩阵Qk=diag(M1,M1,M2),其中M1=q1T[T2/3,T/2;T/2,1]，M2=q2TI，q1=0.1 m2s-3和 q2=1.75×10-4s-3为过程噪声强度参数；T=1 s为量测时间间隔。

地面坐标系原点的测量雷达获取目标斜距η和方位角θ的信息。测量向量为 yk=[ηkθk]T，满足

其中wk∼N(0,Rk)为量测噪声，Rk=diag()为其协方差阵，ση=10 m 和为雷达斜距量测噪声和方位角量测噪声的标准差。

假设初始时刻t0=1 s，目标分别在t=25 s和t=75 s进行一次加强机动，持续时间2 s，大小为：

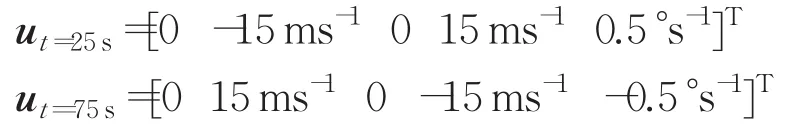
进行200次蒙特卡洛打靶实验，打靶时间为100 s，初值 X0=[1 000 m,300 ms-1,1 000 m,0 ms-1,-3°s-1]T，P0|0=diag[100 m210 m2s-2100 m210 m2s-2100 mrad2s-2],角速度设置为Ω=-3°/s。每次实验的初始状态估计由满足均值为、协方差为 P0|0的高斯正态分布N(;P0|0)随机生成。分别采用 CKF、GHCKF、IMM-CKF、ACKF和AGHCKF对目标进行跟踪。其中IMM-CKF采用匀速运动模型（CV）和协调转弯模型（CA）来描述目标运动，模型初始化概率μ0={0.9 0.1}，模型转移概率：

定义位置均方根误差和均方根误差均值分别为：

其中，(,)和(,)分别为第i次打靶时第 k时刻的目标真实位置分量和估计值；N为打靶次数。同理，可以定义速度均方根误差RMSEvel和均方根误差均值MRMSEvel以及转速均方根误差RMSEomg和均方根误差均值MRMSEomg。

图3为目标的“C”型平面运动轨迹，图中，“I”表示轨迹起点，“F”表示轨迹终点，“○”表示目标机动位置。图4为第一次机动时五种算法的目标跟踪轨迹，由图可知，当目标发生机动时，AGHCKF算法所估计的跟踪轨迹与真实轨迹最为贴近，具有较强的抗干扰能力和更高的跟踪精度。

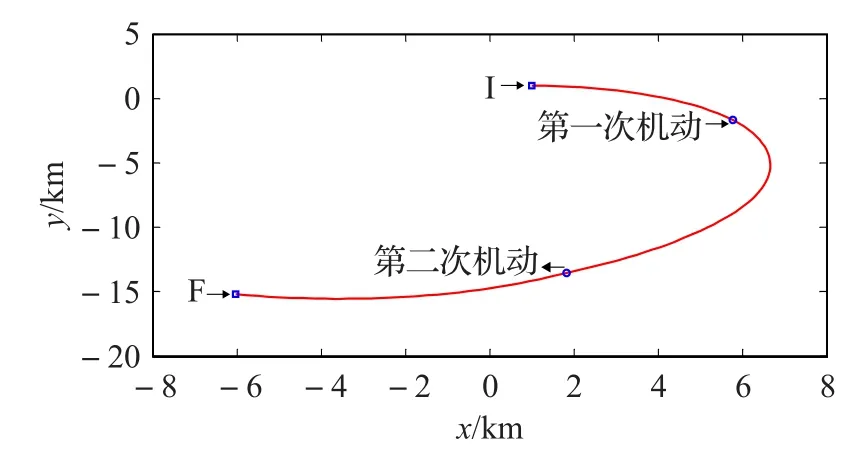
图3 “C”型平面运动轨迹

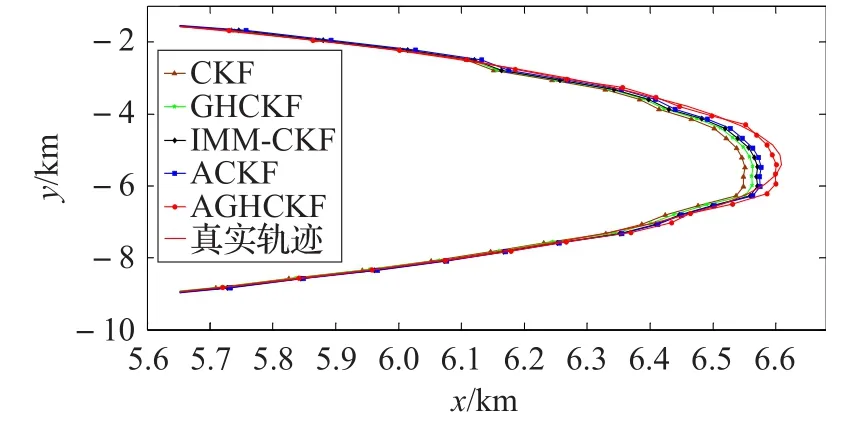
图4 第一次机动时五种算法的目标跟踪轨迹（局部图）

图5 至图7为5种滤波方法对目标位置、速度和转速的均方根误差的对比结果。

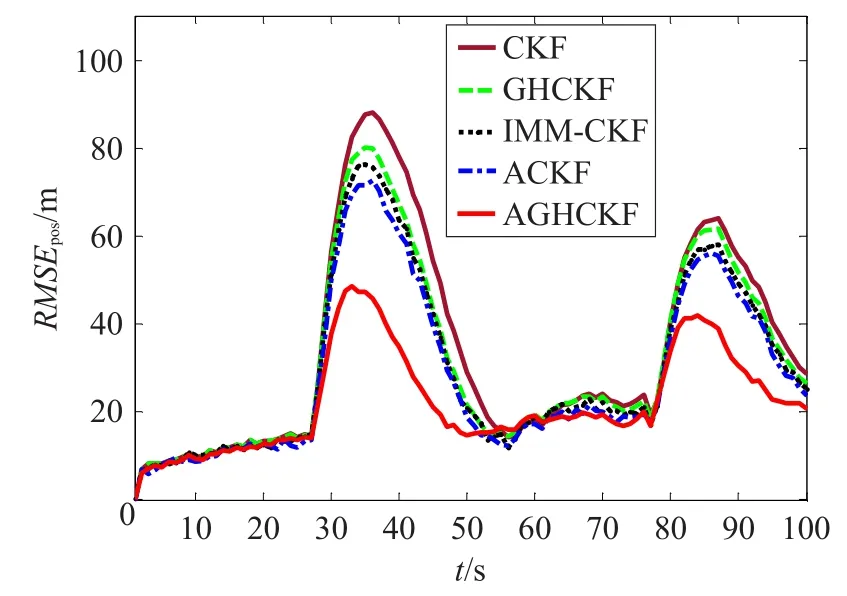
图5 目标位置的估计均方根误差

由仿真结果可以看出本文所提AGHCKF算法对于目标位置、速度和转速的估计均具有较小的均方根误差，滤波效果较好。

图7 目标转速的估计均方根误差

目标在第25 s和75 s加强机动时，CKF和GHCKF的估计误差立即增大，且收敛缓慢。原因是状态突变后，目标真实的运动状态与运动模型不再匹配，基于模型的时间更新过程引入较大误差，协方差阵无法准确反映目标真实状态，也不能根据测量信息进行调整，算法的估计性能受到影响，跟踪精度下降。IMM-CKF算法虽然使用交互的多个模型描述目标运动，仍无法准确描述目标的突变过程，不精确和不完备的模型集合导致误差仍然较大。ACKF和AGHCKF的估计误差增大幅度较小，虽然目标状态的突变导致了系统模型失准，但由残差的方差阵而得到的λk根据残差的变化实时调整增益矩阵Kk，提取残差序列中的有效信息，迫使输出的残差序列正交，较为准确的测量信息在测量更新中的比重得到提高，降低了模型失准造成的状态一步预测估计误差的比重，提高了跟踪精度。同时，AGHCKF采用更精确的容积准则，其计算精度优于ACKF。

表1定量分析了5种方法对目标位置、速度和转速的滤波均方根误差均值MRMSE、使用的容积点个数。可以看出，5种算法均能有效处理文中给出的强非线性系统。（1）对于采用三阶容积规则的ACKF、IMM-CKF、CKF，均可以达到三阶精度，但ACKF加入了自适应渐消因子，滤波器可以更好地处理状态突变的情况，因此具有更高的滤波精度；（2）ACKF和AGHCKF均在算法当中加入了自适应因子，对于系统存在较大状态突变的问题，两者均能取得较高的滤波精度，但是采用广义高阶容积规则的AGHCKF表现明显优于ACKF，这也进一步证实了广义高阶容积准则在滤波精度方面的优越性。

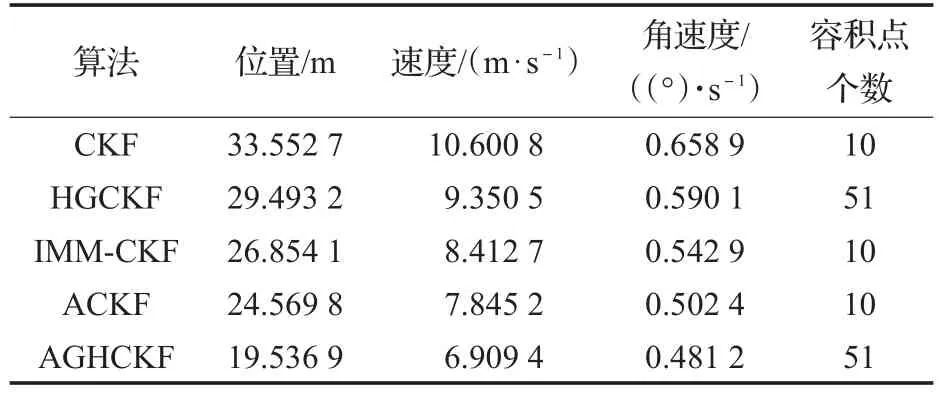
表1 5种滤波方法的均方根误差均值对比

图8对比了5次仿真中各滤波方法计算所消耗的CPU时间。IMM-CKF采用多模型进行滤波增加了计算量，需要较长的执行时间。而GHCKF和AGHCKF因为在时间更新和测量更新计算中采用51个容积点，因此执行时间大于其他3种方法。同时λk的引入也增加AGHCKF的计算量。

图8 5种滤波方法的执行时间

5 结束语

提出了一种基于广义高阶容积规则和矩阵对角化变换的AGHCKF算法。通过引入STF方法中的自适应渐消因子，减少了因系统状态突变造成的估计精度下降的幅度。将该方法用于具有状态突变的目标跟踪中，仿真结果表明，当目标发生加强机动时，AGHCKF相对于CKF和GHCKF具有更强的鲁棒性和系统自适应能力，且估计精度和状态跟踪能力也优于IMM-CKF和ACKF，表现出良好的滤波性能。

参考文献：

[1]Arasaratnam I，Haykin S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control，2009，54（6）：1254-1269.

[2]王世元，黄锦旺，谢智刚，等.非线性卡尔曼滤波器原理及应用[M].北京：电子工业出版社，2015：39-96.

[3]Bar-Shalom Y，Li X R.Estimation with applications to tracking and navigation[M].[S.1.]：John Wiley&Sons，Inc，2001.

[4]Julier S，Uhlmann J，Durrant-Whyte H F.New method for nonlinear transformation of means and covariance in filters and estimators[J].IEEE Transactions on Automatic Control，2000，45（3）：477-482.

[5]王建文，李迅.递归贝叶斯估计框架下的非线性滤波算法综述[J].计算机科学，2010，37（8）：21-25.

[6]熊茂涛，吴钦章.自适应理论在目标跟踪中的应用[J].计算机工程与应用，2009，45（2）：31-34.

[7]权太范.目标跟踪新理论与技术[M].北京：国防工业出版社，2009：17-34.

[8]Jia B，Xin M，Chen Y.Higher-degree cubature Kalman filter[J].Automatica，2013，49（2）：510-518.

[9]孙妍，鲁涤强，陈启军.一种基于强跟踪的改进容积卡尔曼滤波器[J].华中科技大学学报：自然科学版，2013（S1）：451-454.

[10]丁家琳，肖建，赵涛.自适应CKF强跟踪滤波器及其应用[J].电机与控制学报，2015，19（11）：111-120.

[11]张龙，崔乃刚，王小刚，等.自适应高阶容积卡尔曼滤波在目标跟踪中的应用[J].航空学报，2015，36（12）：3885-3895.

[12]郑晓飞，郭创，秦康，等.有色量测噪声下的HCKF及 其应用[J].计算机工程与应用，2017，53（14）：263-270.

[13]Liu J，Cai B G，Wang J.Cooperative localization of connected vehicles：Integrating GNSS with DSRC using a robust cubature kalman filter[J].IEEE Transactions on Intelligent Transportation Systems，2017，PP（99）：1-15.

[14]Zhang X C，Teng Y L.A new derivation of the cubature Kalman filter[J].Asian Journal of Control，2014，16（5）：1501-1510.

[15]Afshari H H，Al-Ani D，Habibi S.A new adaptive control scheme based on the Interacting Multiple Model（IMM）estimation[J].Journal of Mechanical Science and Technology，2016，30（6）.