求距离的三种方法

文 /苗学军

在现实生活中，常常遇到求距离的问题.下面介绍利用三角形求距离的三种方法,供你学习时参考.

一、利用等腰三角形的等角对等边求距离

例1如图1，上午8时，一艘轮船从A处出发以每小时20海里的速度向正北航行，10时到达B处，则轮船在A处测得灯塔C在北偏西36°，航行到B处时，又测得灯塔C在北偏西72°，求从B到灯塔C的距离.

解：AB=20×（10-8）=40（海里），

∵∠CBD=72°，∠A=36°，

∴∠C=∠CBD-∠A=72°-36°=36°，

∴∠C=∠A=36°，∴BC=AB=40（海里）.

∴从B到灯塔C的距离是40海里.

图1

二、利用勾股定理或三角函数求距离

例2在底面直径为2cm，高为3cm的圆柱体侧面上，用一条无弹性的丝带从A至C按如图2所示的圈数缠绕，则丝带的最短长度为_____cm．（结果保留π）

解：∵圆柱体的侧面展开图是矩形（如图3），把图3中的AE，E′C拼成一条线段，当如图4所示时，丝带最短，其中AB为圆柱的底面圆周长的1.5倍，BC为圆柱的高.

∴AB=2π×1×1.5=3πcm，BC=3cm，

在Rt△ABC中，

图2

图3

图4

填

例3如图5，湿地景区岸边有三个观景台A，B，C，已知AB=1400米，AC=1000米，B点位于A点的南偏西60.7°方向，C点位于A点的南偏东66.1°方向.

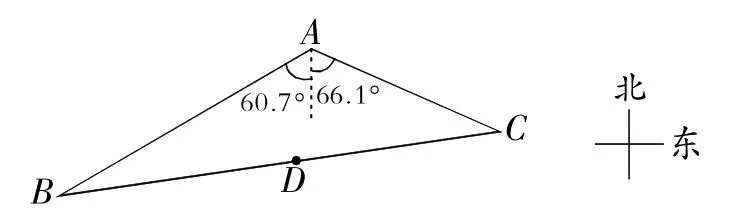
图5

（1）求△ABC的面积；

（2）景区规划在线段BC的中点D处修建一个湖心亭，并修建观景栈道AD.试求A，D间的距离.（结果精确到0.1米）

（参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin60.7°≈0.87，cos60.7°≈0.49，sin66.1°≈0.91，cos66.1°≈0.41，≈1.414）

解：（1）过点C作CE⊥AB，交BA的延长线于E，如图6.

由已知可得，∠BAC=60.7°+66.1°=126.8°.

∴∠CAE=180°-126.8°=53.2°，

图6

在Rt△ACE中，由

CE=1000×sin53.2°≈800（米），

（2）连接AD，过点D作DF⊥AB，垂足为F，则DF∥CE.

又因为D是BC的中点，所以

在Rt△ACE中，由得，AE=1000×cos53.2°≈600（米），

在Rt△ADF中，由勾股定理得

∴A，D间的距离是565.6米.

三、利用比例线段求距离

例4“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图7获得，则井深为（ ）

A．1.25尺. B．57.5尺. C．6.25尺. D．56.5尺.

解：依题意可得 BC∥ED，所以△ABF～△ADE，

∴ AB∶AD=BF∶DE，即5∶AD=0.4∶5，

解得AD=62.5，

∴BD=AD-AB=62.5-5=57.5（尺）．选B．

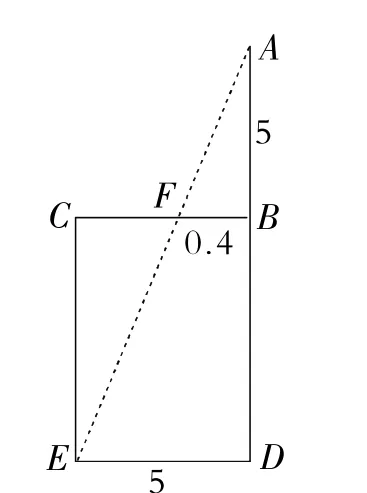
图7