中考试题中的面积问题与方法
广东省中山市教育教学研究室(528400) 周曙
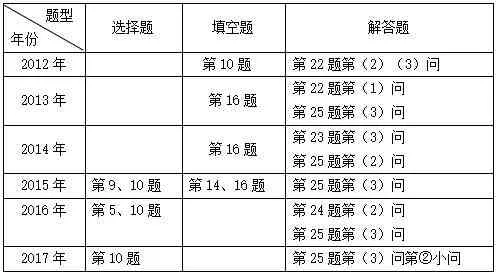
按照义务教育数学课程标准的要求,小学阶段学生初步掌握长方形、正方形、三角形、平行四边形、梯形与圆的面积公式,并能解决简单的实际问题.初中阶段与面积有关的教学内容只有以下两条:会计算圆的弧长、扇形的面积;了解相似三角形面积比等于相似比的平方.但近年来,广东省中考试题中关于面积的题目屡见不鲜,详情见下表:
?
由上表可见,面积问题在近几年广东中考试题中年年出现,而且基本上都是在选择、填空和解答题的最后一题的位置,其重要性可见一斑.由于初中阶段没有系统的学习与归纳面积方法,以致学生答题过程中常常感到无从下手,本文试图对近几年的中考试题进行分析,对常见的面积问题与方法加以归纳,供初三复习备考时参考.
一、直接利用面积公式求面积
例1 (广东省2015年第9题)如图1,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.6 B.7 C.8 D.9
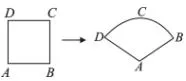
图1
此题考查的是扇形面积公式.解题关键是发现图中正方形和扇形之间的两个关系:(1)周长相等;(2)扇形的半径与正方形的边长相等.由正方形周长得到扇形的周长等于12,由正方形边长得到扇形的半径等于3,由扇形的周长和半径得到弧长等于6,代入扇形面积公式得扇形面积为9.答案为D.
例2 (广东省2013年第22题)如图2,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形顶点C.
(1)设 Rt△BCD的 面 积 为S1,Rt△BFC的 面 积 为S2,Rt△DEC的面积为S3,则(用“>”、“=”、“<”填空);
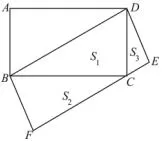
图2
(2)写出题22图中的三对相似三角形,并选择其中一对进行证明.
此题第(1)问考查的是三角形和矩形的面积公式.由已知条件无法求出S1,S2和S3的值,但是可以根据三角形的面积公式和矩形的面积公式判断S1是矩形BDEF面积的一半,进而得到S2+S3也是矩形BDEF面积的一半,所以得到S1与S2+S3的相等关系.
二、利用面积之和(差)求面积
例3 (广东省 2012年第10题)如图3,在平行四边形ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连结CE,则阴影部分的面积是____(结果保留π).
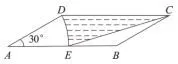
图3
此题阴影部分为不规则图形,解题关键是将阴影部分的面积转化成面积之差,即S阴影=S平行四边形ABCD−S扇形DAE−S△BCE,通过计算得到阴影部分的面积为
例4 (广东省 2014年第 16题)如图4,△ABC绕点A顺时针旋转 45°得到 △A′B′C′,若∠BAC=90°,则图中阴影部分的面积等于___.
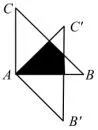
图4
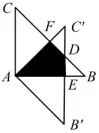
图5
此题阴影部分是不规则的四边形,解题关键是能够将阴影部分的面积转化成面积之差或面积之和.这道题既可利用△ABF与△BDE的面积之差求得阴影部分的面积是也可利用三角形△ADE与△ADF的面积之和求得.
三、利用三角形边长、高与面积之间的关系求面积
例5 (广东省2017年第10题)如图6,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:S△ABF=S△ADF;S△CDF=4S△CEF;3S△ADF=2S△CEF;△ADF=2S△CDF,其中正确的是()
A.B.C.D.
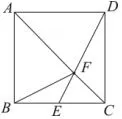
图6
两个三角形如果底相同或相等,则三角形的面积比等于高的比.如果高相同或相等,则三角形的面积比等于底的比.根据正方形的性质可判断△AFD和△AFB属于同底等高的三角形,所以面积相等,故正确,由BE=EC=所以S△ADF=2S△CDF,S△CDF=2S△CEF,S△ADF=4S△CEF,故正确,错误.答案为C.
例6 (广东省2015年第16题)如图7,△ABC三边的中线AD,BE,CF的公共点G,若S△ABC=12则图中阴影部分面积是____.
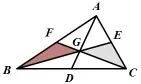
图7
此题阴影部分两个三角形都不是特殊三角形,边长也不易求得,题设条件是△ABC的面积及中线,可以根据中线的性质得到线段之间的关系,进而得到面积之间的关系.根据AD,BE,CF是△ABC三边的中线可以得到所以S△BFC−S四边形BDGF=S△BDA−S四边形BDGF,即S△CDG=S△AFG,同理可得S△AEG=S△BDG.又因为点D,E,F分别是BC,AC,AB边上的中点,所以得到S△BDG=S△CDG,S△CEG=S△AEG,S△AFG=S△BFG.根据等式的传递性得S△BDG=S△CDG=S△CEG=所以,阴影部分的面积为4.
四、利用图形全等或相似求面积
例7 (广东省2013年第16题)如图8,三个小正方形的边长都为1,则图中阴影部分面积的和是___.(结果保留π)
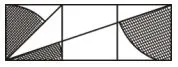
图8
此题右下阴影部分和左下阴影部分都不是特殊角的扇形,不能直接利用扇形面积公式,注意到左下阴影部分与右上小扇形全等,恰好补成一个圆心角为90°的扇形,因此利用割补法可求左下阴影部分与右下阴影部分的面积和为再与左上阴影部分扇形面积相加得出结果:
例8 (广东省 2011年第 10题)如图 (1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取 △ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图 (2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为____.
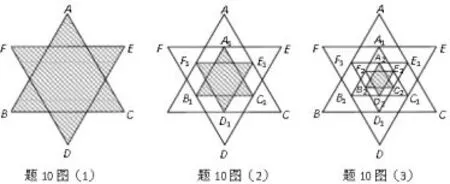
图9
此题属于规律探索题,解题关键是能够判断图中正六角星形相似并找到相似比.利用相似图形的面积比等于相似比的平方,得到这些正六角星形的面积依次为……即正六角星形A4F4B4D4C4E4的面积为
五、一般图形转化为特殊图形求面积
例9 (2014年第 23题)如图10,已知B(−1,2)是一次函数y=kx+b与反比例函数0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
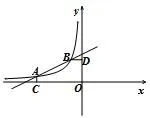
图10
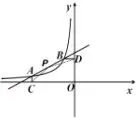
图11
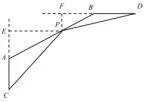
图12
此题第(3)问考查在直角坐标系中求三角形面积的问题.关键是会把一般图形转化为特殊图形,利用点的坐标得到线段的长度.常用的点的坐标和线段之间的关系是:平行于x轴的线段长等于线段两个端点的横坐标差的绝对值,平行于y轴的线段长等于线段两个端点的纵坐标差的绝对值,常用辅助线做法是过已知点作坐标轴的垂线段.
虽然△PCA和△PDB都不是特殊的三角形,但是AC和BD分别与x轴,y轴平行,所以过点P作AC延长线的垂线PE,过点P作BD延长线的垂线PF.局部图形分解出来如图12所示.设P点坐标为(x,y),则PE=x+4,PF=2−y,利用△PCA和△PDB面积可以列出方程进行求解.
例10 (广东省2015年第25题)如图13,在同一平面上,两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm.
(1)填空:AD=____(cm),DC=____(cm);
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B的方向运动,当N点运动到B点时,M,N两点同时停止运动,连结MN,求当M,N点运动了x秒时,点N到AD的距离(用含x的式子表示);
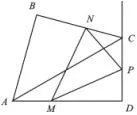
图13
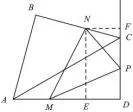
图14
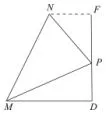
图15
(3)在(2)的条件下,取DC中点P,连结MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存_在最大值,请求出这个最大值.(参考数据:
近几年,中考压轴题都是与面积有关的函数综合题.这类问题的解题关键是能够在复杂的图形背景中识别出常见的基本图形,把一般图形转化为特殊图形.
此题第(3)问中三角形PMN不是特殊的三角形,如图二可以过点N作NF⊥CD于点F,将三角形PMN的面积问题转化成直角梯形MDFN与直角三角形MDP和直角三角形NFP的面积之差,即S△PMN=S梯形MDFN−S△MDP−S△NFP.局部分解出来如图15所示.此题计算量比较大,结果形式复杂,对学生的运算能力要求比较高.
面积是初中数学中一个非常重要的概念,解决面积问题的主要方法是转化,将一般图形转化为特殊图形,将面积问题转化面积之和或面积之差.在转化的过程中可以培养学生的几何直观、推理能力,又可以渗透模型思想、符号意识.直角坐标系中的面积问题要善于利用线段长度与坐标之间的关系,在初中数学总复习中,设计与面积问题有关的专题复习课,引导学生对面积问题进行梳理分类,对解题方法进行归纳总结,可以进一步完善学生的知识结构,提升解决问题的能力.
———《扇形的认识》教学廖

