旋转弹体马格努斯效应数值模拟方法研究

陈白冰，骆振华，袁振宇，蒋晓磊，陈兵

(1.中国兵器工业集团 西安现代控制技术研究所，西安 710065) (2.西北工业大学 航空学院，西安 710072)

0 引 言

导弹、火箭弹等武器在飞行过程中，通常会绕着自身体轴高速旋转来提高飞行稳定性，增加飞行轨迹的精度。这种锥进运动在保证了飞行性能的同时也带来了负面效应，当弹体存在攻角时，由于旋转引起的弹体表面流场相对攻角平面不对称，产生垂直于该平面的力和绕重心的力矩。该现象由德国科学家马格努斯首先发现，故将该力和力矩称为马格努斯力和力矩[1-3]。马格努斯效应产生的主要原因有二：一是旋转引起的附面层畸变，即附面层位移厚度沿着弹体周向发生变化；二是离心力因素。由于马格努斯效应影响很大，因此准确预测其力和力矩，减小其对飞行的影响，是当前研究弹体流场特性的热点之一。

目前，使用CFD方法开展弹体马格努斯力矩效应数值计算已经成为一种常用方法，国内外也取得了很多进展和成果。国外，W.B.Sturek等[4]基于薄层假设，对尖锥等旋成体的马格努斯效应进行了数值计算分析，研究了几何参数的变化对弹丸气动特性的影响；C.J.Nietubicz等[5]基于动态网格技术，对跨声速弹丸的马格努斯效应进行了数值模拟，分析了不同参数对该效应的影响；M.Muto等[6]基于数值方法对反马格努斯效应引起的边界层转捩现象进行研究，揭示了高速旋转的弹丸的边界层流动细节；D.Klatt等[7]则对超声速飞行的旋转弹丸的马格努斯现象进行了研究，使用的方法为非结构网格动态重构模拟旋转运动，对比试验结果分析了激波现象；S.I.Silton[8]对弹丸的亚跨超声速时的马格努斯效应进行了模拟，马格努斯力及力矩结果相比升阻力系数较试验值偏差较大，说明旋转效应的模拟精度还有待提升；自2004年开始，J.Despirito[9]使用DES模型开展了M910旋转弹丸的马格努斯力矩效应研究，得到了更为精确的计算结果。国内，尽管起步较晚，但进展迅速。陈东阳等[10]利用Fluent软件的动网格技术，对带有结构误差的M910弹丸的马格努斯效应进行了数值计算，分析了质量不对称引起的马格努斯力偏差；刘周等[11]利用DES方法对弹丸在大攻角时的马格努斯效应进行了计算分析；雷娟棉等[12]基于滑移网格方法、马杰等[13]使用滑移动网格方法对SOCBT弹丸的气动特性进行了研究，提出并验证了适用于小攻角、超声速情形的弹丸马格努斯力和力矩系数经验公式。

上述研究均基于较复杂的计算方法，例如动网格、滑移网格等，尽管精度较高，但分析效率相对较低，限制了这些方法在弹体快速设计中的应用。

本文针对该问题，使用一种简化的定常求解方法——旋转壁面法，进行弹体马格努斯效应的快速模拟，并与试验值进行对比分析；针对影响马格努斯效应的附面层堆积，开展附面层网格节点数和不同计算模型的适应性研究，对比分析这些因素对本文方法的影响。

1 计算方法

1.1 常用方法

为了计算弹体的旋转效应，常用的方法有三种：①基于刚性动网格技术的非定常计算方法，②基于滑移网格的非定常计算方法，③基于滑移网格的准定常计算方法。其中，基于刚性动网格的非定常计算方法将整个流场域视为刚性的整体，网格跟随弹体的旋转而转动，这样处理的好处是网格的拓扑结构不因旋转而发生改变，但是外边界处会附加旋转速度，该方法如图1所示；基于滑移网格的非定常方法将流场域划分为动、静两部分，动域按照设定的旋转方式进行运动，动静域之间通过交界面进行数据传递，动域的网格整体运动，因此计算网格质量较高，该方法也是一种较为精确的计算方法，如图2所示；基于滑移网格的准定常计算方法是将旋转参考系附加到滑移网格上，此时动域的网格并不会真正旋转，这种准定常方法是一种简化的高效方法，如图3所示。

图1 刚性动网格

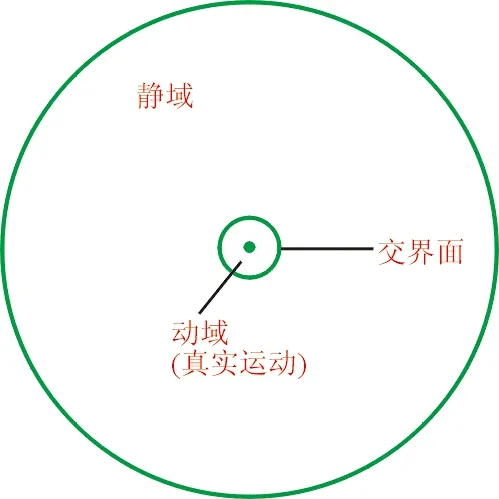
图2 滑移动网格

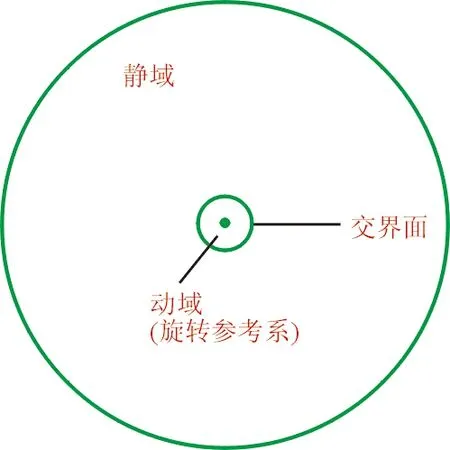
图3 旋转参考系方法

1.2 基于旋转壁面法的马格努斯效应计算方法

图4 旋转壁面法

本文计算全部使用ANSYS FLUENT软件完成。为了提高计算速度和收敛性，计算时先进行无旋工况的模拟，此时的边界条件设置如图5所示。在此基础上设定弹体壁面的旋转速度和转轴，继续计算得到此工况的马格努斯力和力矩，旋转情形的边界条件设置如图6所示。

图5 无旋转情形边界条件

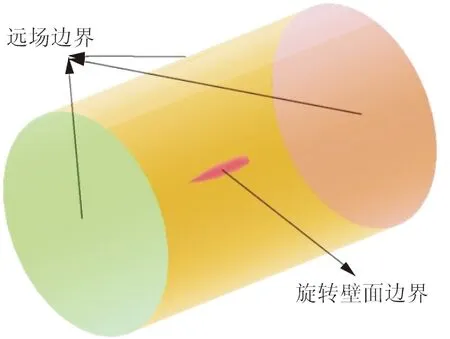
图6 旋转情形边界条件

旋转壁面法并不是一种很新的方法，在计算流体领域多有应用，但是在多对称面弹体的马格努斯力矩数值计算方面却鲜少涉及。本文将该方法引入旋转弹体的流场计算中，形成一种简化的快速马格努斯力矩计算方法。需要注意的是，该快速计算方法主要用来计算多对称面的旋成体马格努斯力矩效应，并不适用于不规则的外形。

1.3 数值方法

采用的控制方程为三维积分形式的雷诺平均N-S方程：

(1)

式中：V为任意控制体；W为守恒变量；F为无粘(对流)通矢量项；Fv为粘性通量；∂V为控制体的边界；n为控制体边界单位外法向矢量；Re为计算的雷诺数。

空间离散采用二阶迎风格式——通量差分分裂(Roe-FDS)格式，采用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)格式迭代求解，应用当地时间步长、残值光顺、预处理和多重网格加速收敛。湍流模型采用对逆压梯度流动模拟精度较高的k-ωSST(剪切应力输运)湍流模型。

2 计算模型及网格

2.1 计算模型

计算模型为一6倍口径弹丸，其名称是Secant-Ogive-Clinder with Boat Tail，简称SOCBT[14]。该模型是评估马格努斯力矩效应的标准模型，由正割风帽头部、圆柱弹身、船尾形尾部三部分构成，船尾收缩角β=7°。其几何模型和尺寸如图7所示。

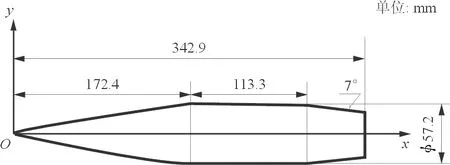
图7 SOCBT弹丸模型

计算坐标系如图8所示。θ=0°为迎风面，θ=180°为背风面。z向的力Cz和绕着y轴的力矩Cmy即为马格努斯力和力矩，其参考点位于弹体头部原点处，参考面积为弹体的最大横截面积Sref=0.002 57m2，参考长度为弹体的最大直径Cref=d=0.057 20 m。

在以往的发展中，由于旅游业在一些项目中利润较高，从业者人数大量的增加，在一定的程度上使得旅游业内部的环境受到了冲击，人们普遍的对于旅游公司以及导游等具有不佳的印象。在大数据时代到来之后，人们在生活的过程中，能够以更加透明的方式对于旅游业内部的情况进行了解。并且在此基础上，无形对于行业的内部构成了一种监督的机制，使得行业内部的环境得到了净化，服务的质量有所提升。

图8 使用的坐标系

2.2 计算网格

计算网格使用ANSYS ICEM CFD软件生成的高质量结构网格，其拓扑结构如图9所示，表面网格和截面网格分别如图10～图11所示。总网格量540万，附面层首层网格高度y+≤1.0。

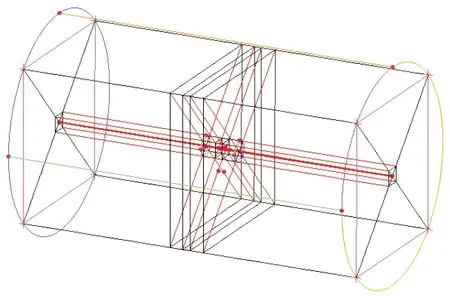
图9 网格拓扑结构

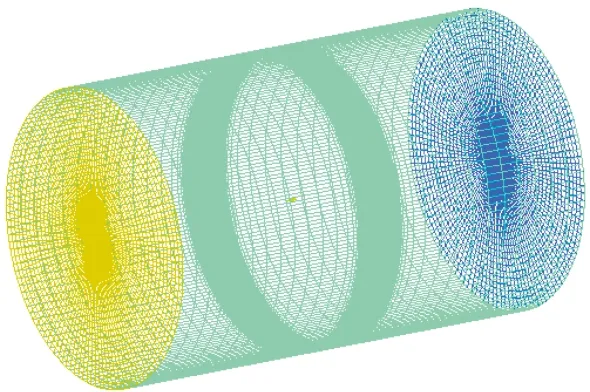
图10 整体计算网格

图11 壁面网格

3 算例与验证分析

3.1 无旋转验证

首先针对无旋工况进行计算，来验证本文数值方法的有效性。计算状态为：来流马赫数Ma=3，大气温度T=310 K，大气压强P=298 500 Pa，攻角α=6.34°。计算得到的弹体对称面以及截面的压力云图分别如图12～图13所示。

图12 对称面压力云图

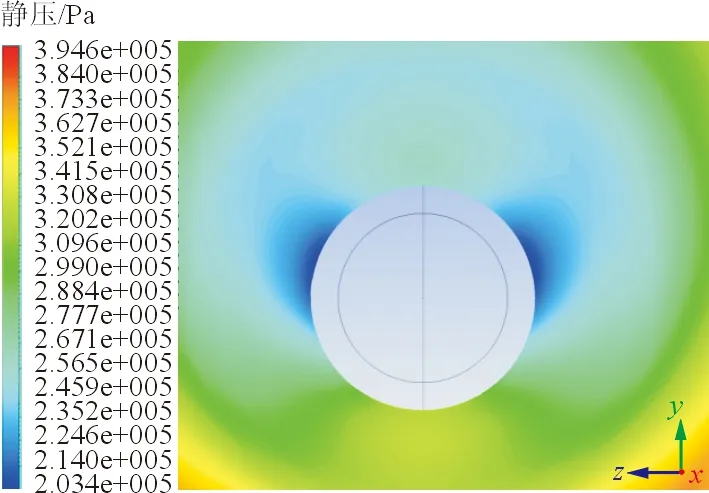
图13 截面x/d=5.77处的压力云图

从图12可以看出：超声速的气流在弹体周围形成多道激波，并在船尾区域形成膨胀波，物理上符合流场的基本规律。

从图13可以看出：无旋时的截面压力分布完全对称。

x/d=4.88和x/d=5.77截面处的详细压力分布分别如图14～图15所示。

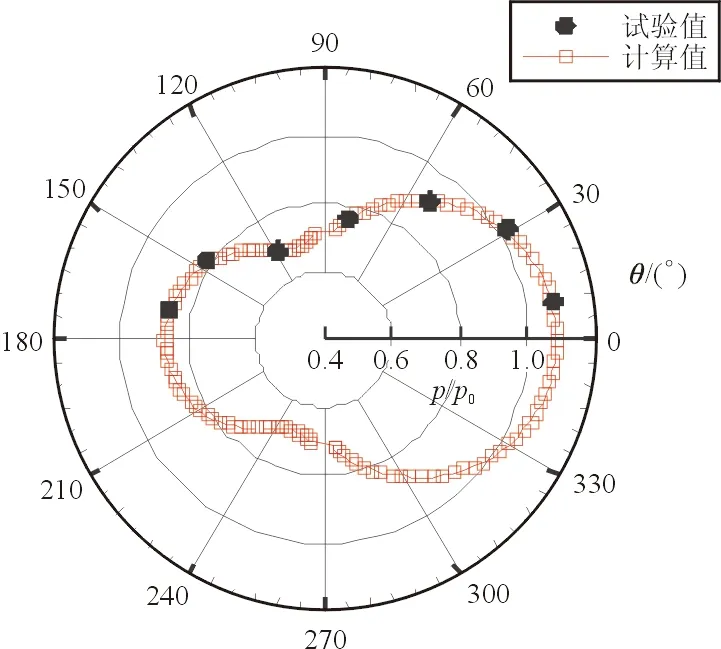
图14 x/d=4.88处的压力对比

图15 x/d=5.77处的压力对比

从图14～图15可以看出：两个截面上的压力计算值与试验值吻合得很好，表明本文的数值方法是有效的。

3.2 旋转时的马格努斯效应

在无旋验证的基础上，使用所建立的旋转壁面法进行弹体的马格努斯力矩效应的数值模拟。计算的攻角为0°、3°、5°、6.34°、7°、10°、12°以及15°。为了保证计算条件与动态试验一致，取无量纲的旋转角速度Ω*=Ωd/V=0.19，其中Ω为实际的旋转角速度。计算得到的各个攻角下的马格努斯力和力矩系数分别如图16～图17所示。

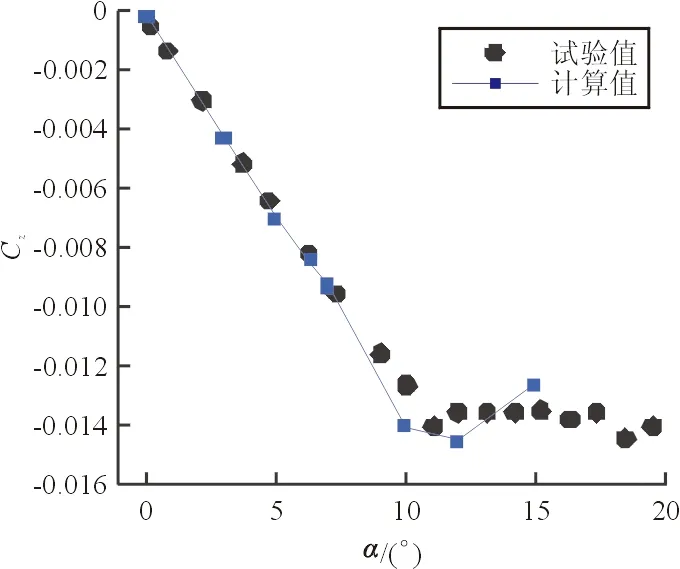
图16 马格努斯力系数

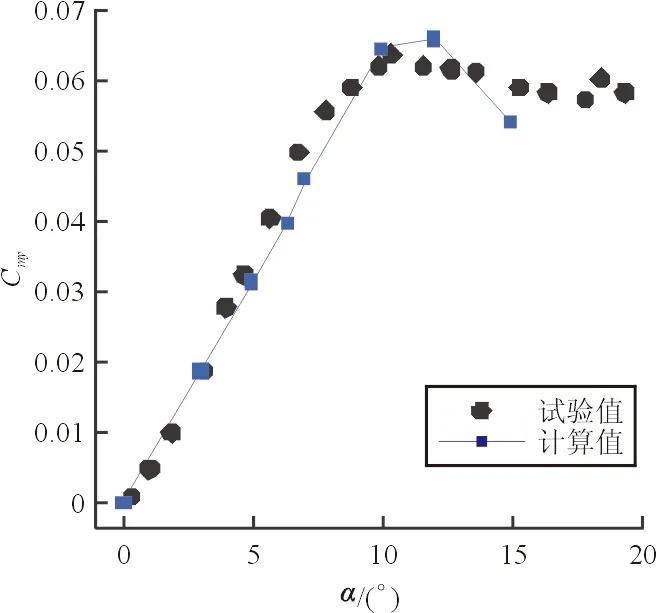
图17 马格努斯力矩系数

从图16～图17可以看出：在中小攻角范围，计算值与试验值吻合较好，随着攻角的增大，弹体背风区出现分离，而本文使用的湍流模型对分离的捕捉能力有限，此时计算结果与试验值的偏差变大。但总体来看，本文的计算方法是有效的。

3.3 数值计算方法影响因素分析

3.3.1 附面层的影响

马格努斯效应产生的主要原因之一是旋转引起的附面层堆积，因此对周向的附面层差异进行足够精确地模拟是获取准确的马格努斯力和力矩的前提。为了准确地描述附面层，需要在附面层内部布置足够的网格节点。分别设定附面层的网格节点数量为21、61和101，对旋转时的流场进行计算。使用的湍流模型仍为k-ωSST模型，以初始攻角α=6.34°的工况为例进行分析。三种模型计算得到的马格努斯力矩系数如表1所示。

表1 不同附面层节点数计算结果对比

从表1可以看出：随着附面层节点数的增加，计算结果与试验值吻合得越好，表明更多的附面层节点能够对堆积效应做出更准确地模拟；而网格节点为61时，其计算结果与节点为101的计算结果差别较小，从减小计算代价的角度考虑，可以选择节点数为61进行模拟。

3.3.2 湍流模型的影响

旋转引起的马格努斯力矩不仅导致了附面层的堆积，而且由于粘性致使堆积区域的分离也直接影响着马格努斯力的准确计算。尤其是随着初始攻角的增大，背风区的分离区域扩大，与堆积区的分离相互干扰，导致整个弹体的流场表现为较复杂的状态。而不同的湍流模型对这种复杂流态的捕捉能力不同，本文选择一方程的S-A模型、两方程的k-ωSST模型和SAS自适应尺度模型[15]进行6.34°攻角和15°攻角的对比计算。其中SAS模型使用类似于DES模型的尺度因子，能够对分离现象做出较为精确的模拟。

6.34°攻角时的计算结果如表2所示，可以看出：由于此时的分离并不特别严重，三种模型的计算结果差别不明显。而15°攻角时的马格努斯力和力矩的对比如表3所示，可以看出：此时差别比较明显，流场背风区出现大范围的分离流动，且与激波形成复杂的干扰；使用SAS模型得到的结果显然更接近试验值，主要是因为该模型相比一般的湍流模型能够捕捉到更为精细、更为准确的分离效应。

表2 6.34°攻角下不同计算模型的结果

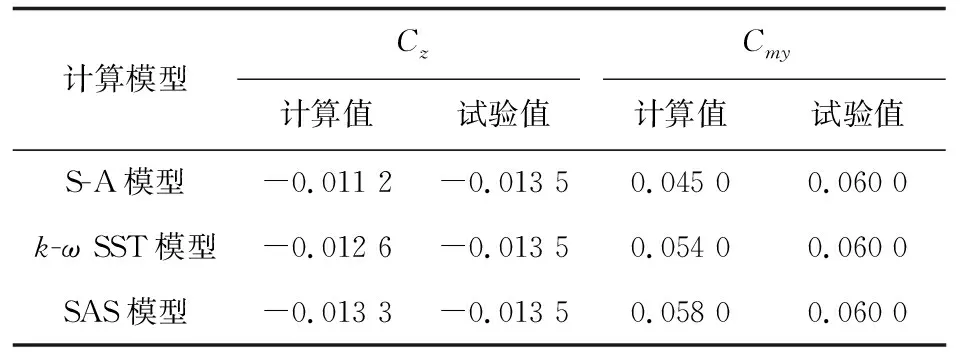
表3 15°攻角下不同计算模型的结果

不同湍流模型的计算表明，为了能够更好地获取弹体的马格努斯力矩效应，对于不同攻角的模拟需要选择不同的计算模型，达到兼顾效率和精度的效果。

4 结 论

(1) 本文提出的基于旋转壁面法的多对称面弹体旋转效应数值模拟方法，不使用动网格和多参考系方法，将旋转速度附加于壁面上，使用定常方法进行计算，效率较高。对旋转弹体的马格努斯力和力矩系数的计算结果验证了方法的有效性。

(2) 马格努斯力矩效应的起因之一是旋转引起的附面层堆积，为了准确地捕捉这种效应，需要在附面层区域布置足够的网格节点。

(3) 大攻角时，旋转引起的附面层堆积同分离区域相互干扰，对于超声速的弹体来讲，还有多重激波的相互掺杂，这种复杂的非线性流场使用一般的湍流模型很难精确模拟，需要借助更高精度的模型，SAS模型作为一种新的大攻角计算方法，使用了类似DES方法的尺度因子，能够在降低网格要求的情形下得到与DES类方法接近的计算效果。

[1] Seifert J. A review of the Magnus effect in aeronautics[J]. Progress in Aerospace Sciences, 2012, 55(5): 17-45.

[2] Zhao J, Hou Q, Jin H, et al. Discussion on improving Magnus effect of cylinder based on CFD[C]∥IEEE International Conference on Mechatronics and Automation. IEEE, 2013: 539-543.

[3] Cayzac R, Carette E, Denis P, et al. Magnus effect: physical origins and numerical prediction[J]. Journal of Applied Mechanics, 2011, 78(5): 748-760.

[4] Sturek W B, Kayser L D, Nietubicz C J, et al. Computations of Magnus effects for a yawed, spinning body of revolution[J]. AIAA Journal, 2012, 16(7): 687-692.

[5] Nietubicz C J, Sturek W B, Heavey K R. Computations of projectile Magnus effect at transonic velocities[J]. AIAA Journal, 2012, 23(7): 15.

[6] Muto M, Tsubokura M, Oshima N. Numerical visualization of boundary layer transition when negative Magnus effect occurs[J]. Journal of Visualization, 2012, 15(3): 261-268.

[7] Klatt D, Hruschka R, Leopold F. Numerical and experimental investigation of the Magnus effect in supersonic flows[C]∥AIAA Applied Aerodynamics Conference, 2013.

[8] Silton S I. Navier-Stokes computations for a spinning projectile from subsonic to supersonic speeds[J]. Journal of Spacecraft and Rockets, 2005, 42(2): 223-231.

[9] Despirito J. CFD prediction of Magnus effects in subsonic to supersonic flow[R]. AIAA-2008-0427, 2008.

[10] 陈东阳, Laith K A, 芮筱亭, 等. 结构误差对旋转稳定弹丸气动特性影响的数值模拟[J]. 空气动力学学报, 2014, 32(5): 705-711.

Chen Dongyang, Laith K A, Rui Xiaoting, et al. Numerical simulation of a spinning stabilized projectile aerodynamic characteristics effected by structure errors[J]. Acta Aerodynamica Sinica, 2014, 32(5): 705-711.(in Chinese)

[11] 刘周, 谢立军, 杨云军, 等. 弹丸旋转空气动力效应非定常数值模拟[J]. 航空学报, 2016, 37(5): 1401-1410.

Liu Zhou, Xie Lijun, Yang Yunjun, et al. Unsteady numerical simulation of aerodynamic effect of a spinning projectile[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1401-1410.(in Chinese)

[12] 雷娟棉, 李田田, 黄灿. 高速旋转弹丸马格努斯效应数值研究[J]. 兵工学报, 2013, 34(6): 718-725.

Lei Juanmian, Li Tiantian, Huang Can. A numerical investigation of Magnus effect for high-speed spinning projectile[J]. Acta Armamenyarii, 2013, 34(6): 718-725.(in Chinese)

[13] 马杰, 陈志华, 姜孝海. 高速旋转条件下的弹丸气动特性研究[J]. 弹道学报, 2015, 27(2): 1-6.

Ma Jie, Chen Zhihua, Jiang Xiahai. Aerodynamic characteristics of a projectile with high spinning speeds[J]. Journal of Ballistics, 2015, 27(2): 1-6.(in Chinese)

[14] Onn S C, Su A, Wei C K, et al. Computational drag and Magnus force reduction for a transonic spinning projectile using passive porosity[J]. Computer Methods on Applied Mechanics and Engineering, 2001, 190(46/47): 6125-6139.

[15] Menter F, Egorov Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1: theory and model description[J]. Flow Turbulence and Combustion, 2010, 85(1): 113-138.