旋转叶片干摩擦阻尼结构模型及分析方法研究综述

秦洁，燕群，黄文超

(中国飞机强度研究所 航空发动机强度研究室，西安 710065)

0 引 言

旋转叶片是航空发动机的关键部件，其振动特性及振动抑制技术对发动机的性能和结构完整性、工作可靠性有重要影响[1-2]，李其汉等[3]分析了导致叶片高循环疲劳失效的原因，指出减小和抑制动力响应是排除或预防叶片高循环疲劳失效的方法。在各类叶片振动抑制方法中，干摩擦阻尼结构应用最为广泛，其利用结构件的干摩擦作用将振动能量转化为热能形式耗散，从而降低结构的振动响应，并具有简单高效、受温度影响较小等优势。由于干摩擦阻尼减振机理和结构系统响应的复杂性，国内外很多学者针对叶片干摩擦阻尼结构进行了大量的研究工作，并取得了丰硕的研究成果。

本文对旋转叶片干摩擦阻尼结构的动力学建模、减振分析进行归纳和总结，以期为旋转叶片减振结构的建模设计、提高可靠性和效率、减振延寿等方面提供理论和技术支持。

1 旋转叶片干摩擦阻尼器动力学建模

1.1 旋转叶片干摩擦阻尼器结构模型

根据叶片干摩擦阻尼结构形式不同，旋转叶片干摩擦阻尼可分为叶冠/凸肩、叶片缘板下摩擦阻尼器、叶片根部(榫头/榫槽)连接、拉筋等。涡轮叶片主要采用叶冠与缘板阻尼块，叶冠/凸肩阻尼主要应用于风扇/压气机转子叶片。众多学者通过不断完善结构模型和分析方法，开展了叶片阻尼结构的动力学特性研究。

1.1.1 叶冠/凸肩结构

航空发动机涡轮叶片采用叶冠设计能够明显改善涡轮性能和振动特性。相邻叶片的叶冠抵紧，并在工作中始终保持一定紧度，利用工作时叶片的反扭变形,使两个锯齿的工作面接触更加压紧,整圈叶片通过叶冠相互作用，并在离心力场中连成一个整体,借助接触面上的接触力和干摩擦力，提高带冠叶片的刚度，可以减小叶片扭转变形和弯曲变形；当叶片产生振动时，相邻叶冠间产生摩擦可以吸收振动能量,起到减振作用[4-5]。

S.T.Choi等[6]将变截面预扭叶片模化为Timoshenko梁，用2个平动弹簧和3个转动弹簧模拟叶片的约束，将叶冠近似为梁顶部的弹簧，提出了涡轮叶片振动分析的修正积分方法(MDQM)，对叶片约束进行动力学分析。

谢永慧等[7]采用扭曲梁单元模型，推导了阻尼围带的刚度和阻尼矩阵，建立了阻尼围带长叶片振动分析模型，采用波传递方法分析了整圈叶片的振动特性。

任兴民等[8]建立了欧拉-贝努利梁-质量-弹簧模型来模拟带平行四边形叶冠的叶片。将系统放入转速引起的离心力场中，研究旋转状态下带冠叶片的动力特性；推导出了考虑离心力、气流激振力及碰摩复合作用的系统动力学方程；基于推导出的方程，研究了叶冠接触角、气流激振力、摩擦因数、刚度比和间隙等参数对统稳态响应的影响规律。

陈璐璐等[9]通过数值计算方法研究凸肩径向/轴向位置、啮合角等结构设计参数对振动特性的影响。凸肩阻尼结构叶片示意图如图1所示[9]。提出啮合角对叶片共振频率的影响远小于凸肩径向/轴向位置，啮合角和初始过盈量对一阶共振频率的影响较小，但它们共同影响接触面的初始正压力，进而决定叶片共振应力的幅值。

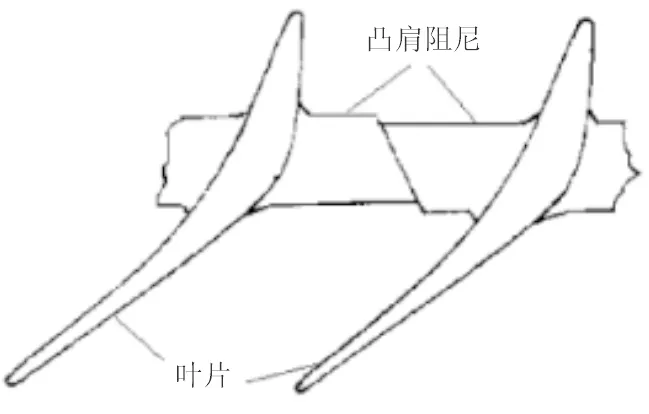
图1 凸肩阻尼结构叶片示意图

1.1.2 缘板阻尼结构

由于叶片工作时工况的复杂性及工艺、装配等因素的影响，实际工作中可能会有凸肩对某些振型未产生减振作用，另外，为了减少气动损失并提高强度，最好采用无凸肩叶片设计，因此发展了缘板阻尼结构。在相邻叶片缘板内侧增加了阻尼结构设计，该结构同时产生阻尼及封严的双重作用，如图2所示[10]。郝燕平等[10-13]、单颖春等[14-15]分析了干摩擦阻尼块在叶片减振方面的应用与发展，并试验研究了缘板摩擦阻尼器的减振效果。

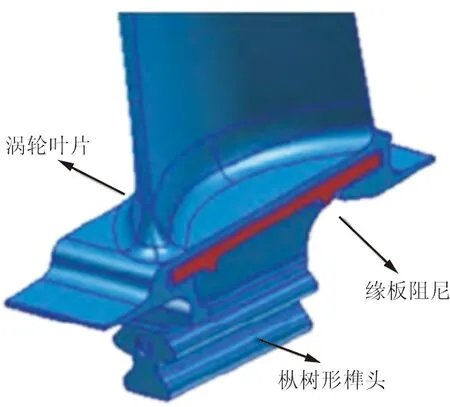
图2 缘板阻尼器

1.1.3 叶片阻尼结构的简化

叶片阻尼结构形式多样，形状、紧度、接触面积等参数使得动力学建模变得复杂，因此有必要对叶片阻尼结构形式进行简化，即叶片-地(B-G)型和叶片-叶片(B-B)型。B-G型阻尼器一端与叶片摩擦而另一端则与刚度较大的零件(例如轮盘等)相连。叶片定位挡圈的摩擦阻尼及叶片根部与盘连接面的摩擦阻尼可划为此类型；B-B型阻尼器的两端与相邻的两个叶片摩擦接触，叶片与阻尼器之间的相对运动与相邻叶片间的相对运动密切相关，叶片凸肩摩擦、叶冠摩擦及缘板摩擦阻尼器都属于这种类型。在动力学分析中，B-B型计算要考虑相邻叶片间的相对运动，可通过数学方法转化为B-G型[16-17]，因此近年来多数以B-G型摩擦阻尼块进行叶片阻尼结构的简化，如图3所示[16]。

图3 B-G型叶片阻尼结构模型

1.2 干摩擦阻尼数学模型

由于摩擦过程的复杂性，目前还没有一种摩擦定律可以完整描述与摩擦有关的所有现象，而建立科学、准确的干摩擦阻尼模型是解决旋转叶片减振分析的关键，干摩擦阻尼系统如图4所示。目前用于描述接触面上作用的干摩擦数学模型主要有两种：Coulomb摩擦模型、“滞后”弹簧摩擦模型。

图4 干摩擦阻尼系统

1.2.1 Coulomb摩擦模型

Coulomb摩擦模型是经典摩擦定律，如图5(a)所示，其力学模型如图5(b)所示，模型中只有摩擦系数和正压力两个参数，未考虑滑动时摩擦面的变形，阻尼器视为刚体，未考虑接触面的刚度，摩擦力是不连续的，在讨论仅有滑动条件下的力学关系较为准确，不适用于相对位移较小的情况。

(a) Coulomb干摩擦模型

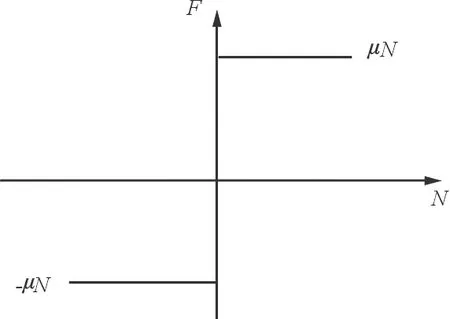
(b) Coulomb干摩擦力学模型

1.2.2 “滞后”弹簧摩擦模型

“滞后”弹簧模型相当于在Coulomb摩擦模型上串联一个弹簧，如图6(a)所示。假设位移x正弦变化时，“滞后”弹簧模型的力与位移的关系轨迹呈闭合的平行四边形，如图6(b)所示。在发动机叶片的一个振动周期内，相当长的时间内摩擦阻尼器是处于粘着(stick)状态[10]，从而阻尼的刚度会对叶片的动力响应产生较大的影响，因此在建立叶片摩擦阻尼器数学模型时必须将阻尼器的刚度加以考虑。L.E.Goodman率先考虑了接触面刚度，认为接触面之间的滑移不是突然发生的，当滑动载荷小于临界摩擦力时，接触点存在一定的弹性变形，叶片仍可以存在一定的振幅，只有当叶片振幅过大，滑动载荷大于摩擦力的时候，摩擦接触点之间才产生相对滑移[18-19]。A.Sinha[20]最早将这种模型用于叶片的摩擦阻尼计算中，并用这种模型对带B-G型摩擦阻尼器的叶片进行了法向正压力的优化研究。

(a) “滞后”弹簧摩擦模型

(b) “滞后”弹簧摩擦力学模型

1.2.3 其他摩擦模型

除了基于传统Coulomb摩擦定律构造的摩擦模型，N.Oden提出了一种积分形式的非局部非线性摩擦定律。A.V.Srinivasan和B.N.Cassenti也对此模型作过研究，采用各向异性权函数对非局部库仑摩擦定律做了修正，A.V.Srinivasan提出了根据摩擦面的相对位移计算摩擦力的方法[21]。亦有学者还考虑了一种摩擦力大小随振动位移、振动速度变化的摩擦模型[22-24]。

1.3 干摩擦阻尼接触模型

叶片的接触是面接触或线接触，可以把干摩擦阻尼接触模型分为宏滑动模型和微滑动模型。

1.3.1 宏滑动模型

宏滑动模型是一种单点接触模型，这种模型假定整个摩擦接触面上的应力、应变场都相等。即在外力的作用下，整个摩擦面同时滑动(slip)或粘着(stuck)，整个摩擦面各点的接触状态及产生的摩擦力即可等价为用一个点的状态和力来表示。按照是否考虑接触面的刚度又分为宏滑动模型-Coulomb模型和宏滑动模型-考虑接触刚度模型。

宏滑动模型-Coulomb模型描述的是理想情况下的干摩擦模型，难以准确估计摩擦阻尼的减振效果；宏滑动模型-考虑接触刚度模型中，当接触面间的正压力较小时，应用这种模型所得的计算结果与试验结果吻合较好。

1.3.2 微滑动模型

为了解决正压力较大时整体滑移模型的局限性，准确描述接触面上应力分布不均，学者们提出了多个接触点描述接触面摩擦接触特性的模型-微滑动模型(如图7所示[25])，微动滑移模型将接触界面离散成多个接触点对，分别求解各个接触点对的运动状态以及由其产生的摩擦约束力，较为精细地描述摩擦接触面的摩擦状态。

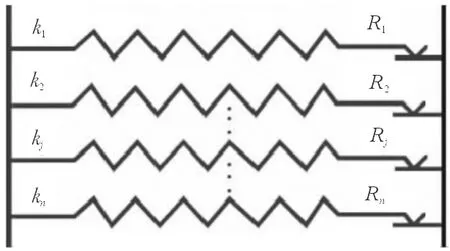
图7 并联微动滑移模型

叶片振动可能只会导致部分接触点发生滑移，而其他接触点扔保持粘滞状态。当外力进一步增加后必然会使整个区域开始整体滑动。微动滑移模型主要有串联、并联两种形式，并联微滑模型中，摩擦力表示为叶片位移的函数，比串联模型更加适合于进行动力分析，工程应用中通常选择这种模型进行研究[25-27]。实际上，微观滑动(即部分滑动部分黏滞的接触现象)对共振响应的抑制比宏观滑移要好[25]。

何尚文等[28]采用具有弹性剪切层的微滑移模型对B-G型叶片缘板阻尼器的减振特性进行了研究。徐自力等[29-30]采用Csaba微滑移摩擦模型研究了结构参数对叶片减振效应影响，为阻尼器设计提供了理论依据。上官博等[31]发展了一种能够考虑接触面摩擦运动过程中正压力随时间变化的微滑移干摩擦模型。

1.4 接触面运动模型

叶片实际工作中，除了弯曲振动，还可能发生扭转振动和耦合振动，因此根据相互运动形式不同，接触运动模型分为一维接触模型、二维接触模型、三维接触模型。

(1) 一维接触模型：表征叶片以单纯的弯曲振型振动时，叶片与阻尼块的相互运动在一条直线上。国内外学者对此类模型研究已取得了丰硕成果[32-34]，并已得到广泛应用[35]，然而，随着研究深入，一维摩擦接触模型不能求解叶片阻尼结构的耦合振动问题的局限性愈加明显。

(2) 二维接触模型：为了描述叶片的扭转振动和耦合振动，必须采用二维接触模型表述接触点的特性。该模型中，假设叶片的接触点运动轨迹可能是圆或者椭圆，阻尼块上接触点的运动轨迹分别为圆或者平面不规则的闭合曲线[36]，然而在复杂的周期性激励下，叶片的运动轨迹很可能不是圆或者椭圆，K.Y.Sanliturk等[37]提出了一种通过跟踪触点运动轨迹，得到界面约束力的二维干摩擦接触模型。

(3) 三维接触模型：在二维接触模型的基础上，考虑接触面沿法向的相对运动，发展了三维干摩擦接触模型，如图8所示。这种模型可以考虑阻尼块形状的影响，但比较复杂，且模型沿法向的变形与切向和轴向相比极小，在建模中应用较少。

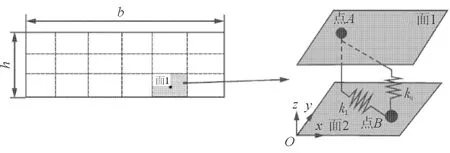
图8 三维干摩擦接触数值模型

2 旋转叶片干摩擦阻尼结构减振特性分析方法

干摩擦阻尼系统在数学上是一个复杂的强非线性系统，通常只有个别简单模型可以求得解析解(例如单自由度干摩擦阻尼系统中不考虑接触刚度的情况)，其他绝大多数模型的分析只能依赖于数值计算。计算方法可以分为数值积分法、谐波平衡法、时频转换法。

(1) 数值积分法

数值积分法基于时域计算，跟踪系统响应的时间历程，为了能够准确反映摩擦面粘滞状态与滑动状态之间的转换，在状态转换点附件需要采用较小的时间步长以保证计算的准确性[38-39]，计算效率不高，常用于检验其他计算方法的正确性。梁明轩等[40]采用数值积分法研究了质量偏心和转速对系统非线性动力学响应的影响，建立了内燃机曲轴轴系弯扭耦合运动微分方程，运用谐波平衡法获得了系统幅频特性，结果表明，谐波平衡法与数值积分法得到的结果吻合较好。

(2) 谐波平衡法

谐波平衡法基于频域计算，假设叶片受到简谐激励时，叶片的振动主要表现为基频振动，同时只保留摩擦力傅里叶级数展开式中的一次项，从而可将干摩擦阻尼系统的非线性微分方程转化为非线性代数方程进行求解。Wang J H等[39,41]采用一阶谐波平衡法对简单干摩擦阻尼系统进行了深入地研究，其研究结果表明，一阶谐波平衡法对于一些简单的干摩擦阻尼系统能够获得较高的计算精度，且其计算效率远远高于直接积分法。为了进一步提高精度，C.Pierre等[42]提出了考虑系统高阶谐波影响的增量谐波平衡法，但是该方法在计算效率上相对于直接积分法并无优势。直到T.M.Cameron等[43]提出求解非线性系统的时频转换法，才使得干摩擦阻尼系统的频域响应求解方法获得了突破性的进展。

(3) 时频转换法

时频转换法综合了时域上直接积分法和频域上谐波平衡法各自的优点，充分利用了在频域中求解代数方程避免卷积运算的高效性和时域中计算非线性力的便利性。J.Guillen[44]和O.Poudou等[45-46]提出了基于时频转换的高阶谐波平衡法，并将该方法用于航空发动机失谐叶盘振动问题的研究中。S.Nacivet等[47]和D.Laxalde等[48]基于时频转换的思想，提出了“动态拉格朗日法”，并对带阻尼环的整体叶盘结构系统进行了较为详细地分析。这两种方法已经成为目前国际上进行干摩擦阻尼系统响应计算的主流分析方法。A.Herzog等[49]和M.Krack等[50]对这两种方法进行了对比，表明这两种方法在计算效率、数值迭代稳定性等方面具有各自的优势。

国内的学者也开展了基于时频转换的高效算法研究。李琳等[51]采用将时频转换法与高阶谐波平衡法相结合的方法对典型航空发动机叶片缘板阻尼器宽频多阶次激励的减振效果进行计算与分析，提出在航空发动机中宽频多阶次激励下的干摩擦阻尼系统进行分析计算时需要保留非线性力的高阶谐波成分，才能获得准确的结算结果。

何尚文等[52]提出一种新的等效线性方法分析干摩擦缘板阻尼系统，将干摩擦力傅里叶分解后，考虑三次谐波用于修正1阶谐波解。丁千等[53]研究了多谐波激励下干摩擦阻尼叶片的振动特性，用平均法推导了系统低阶谐波共振下的稳态响应方程，分析初始压力对抑制叶片共振响应的效果。卢娜等[54]参考实验结果将正压力过大时干摩擦力与位移简化为线性关系，对整体滑动模型进行完善。在考虑了阻尼器刚度系数、接触面正压力以及外激励幅值等的影响因素下，结合一次谐波平衡法对缘板干摩擦阻尼器进行了仿真分析。张亮等[55]采用谐波平衡法对单个扇区三自由度整周失谐叶-盘进行振动特性分析，讨论了叶根干摩擦对失谐叶盘系统振动特性的影响。

3 研究展望

在借鉴成熟摩擦接触理论的基础上，提出多种带冠/凸肩叶片、缘板阻尼叶片模型，将接触处理成等效刚度、等效阻尼后，建立动力学方程或者进行有限元数值计算，还有部分学者不断完善摩擦接触理论，建立更为丰富的干摩擦阻尼数学模型和接触模型，形成非线性振动响应求解方法，在一定范围内为减振结构的建模设计、提高可靠性和效率、减振延寿等方面提供理论和技术支持。

但考虑到不同的叶片干摩擦阻尼减振的复杂情况，例如可能出现的多叶片干摩擦阻尼减振、复杂激励、干摩擦接触时变性、摩擦生热、阻尼变形等，关于叶片干摩擦阻尼减振过程的建模，仍需要考虑更多的影响因素，进一步研究可从以下方面进行：

(1) 对于“滞后”弹簧摩擦模型，从经典库伦摩擦模型出发，考虑一个或多个激励周期内接触界面经历多次接触-脱离运动连续性、摩擦产生的热效应、磨损造成的间隙和接触发生变化等实际情况，修订摩擦过程中的不同运动状态的转换位置，建立适合激励周期内的典型工况的摩擦模型。

(2) 对于微滑动模型，通过求解各个接触点对的运动状态以及由其产生的摩擦约束力，较为精细地描述接触面的摩擦状态。考虑干摩擦接触时的时变性、叶片阻尼块发生变形，找到摩擦因数随叶片阻尼块几何尺寸、转速、材料特性有关的显性表达式，通过试验确定摩擦因数随不同参数的变化规律，用以修订摩擦因数表达式。

(3) 对于接触面运动模型，基于叶片和阻尼块相互运动形式不同，从叶片振型出发，考虑时变刚度和阻尼的存在使一个振动周期内振型发生突变的问题以及摩擦与耦合振动，形成可有效支撑高效动力学分析的二维接触模型。

(4) 减振特性分析方面，在开展基于时频转换的高效算法的基础上，研究非线性摩擦力的高次谐波对振动响应的影响。

(5) 考虑到叶片阻尼结构几何及运动状态的复杂性，基于摩擦接触界面的计算理论来模拟，可以更好地模拟真实的叶片阻尼结构减振，计算可在成熟的商业有限元软件进行，通过设置接触面和目标面，设置接触约束条件，选择接触约束算法，选择一定的接触算法来完成叶片阻尼结构接触动力学计算。

4 结束语

对旋转叶片干摩擦阻尼结构的模型及分析方法进行了比较全面的综述，重点讨论了多种旋转叶片干摩擦阻尼结构动力学建模和减振分析方法。提出应在以下方面进行研究：建立适合激励周期内的典型工况的摩擦模型；通过试验修订摩擦因数表达式；形成可有效支撑高效动力学分析的二维接触模型；研究非线性摩擦力的高次谐波对振动响应的影响。

[1] Duffy K P, Choi B B, Provenza A J, et al. Active Piezo-electric vibration control of subscale composite fan blades[J]. Journal of Engineering for Gas Turbines and Power, 2012, 135(1): 1217-1226.

[2] Svendsen M N, Krenk S, Hogsberg J. Resonant vibration control of rotating beams[J]. Journal of Sound and Vibration, 2011, 330(9): 1877-1890.

[3] 李其汉, 王延荣, 王建军. 航空发动机叶片高循环疲劳失效研究[J]. 航空发动机, 2003, 29(4): 16-18.

Li Qihan, Wang Yanrong, Wang Jianjun. Investigation of high cycle fatigue failure for the aero engine blades[J]. Aeroengine, 2003, 29(4): 16-18.(in Chinese)

[4] 孙立业. 航空发动机涡轮工作叶片锯齿冠结构设计研究[R]. 沈阳: 中国航空工业第一集团公司第六○六研究所, 2005.

Sun Liye. Design investigation of elastically supported turbo-machinery blades in areoengine[R]. Shenyang: AVIC606, 2005.(in Chinese)

[5] 何榜. 带锯齿冠涡轮叶片振动特性分析及结构优化设计研究[D]. 南京: 南京航空航天大学, 2007.

He Bang. Research on dynamic characteristic and structural optimization design of turbine blade with zigzag-shroud[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2007.(in Chinese)

[6] Choi S T, Chou Y T. Vibration analysis of elastically supported turbo-machinery blades by the modified differential quadrature method[J]. Journal of Sound and Vibration, 2001, 240(5): 937-953.

[7] 谢永慧, 张荻. 汽轮机阻尼围带长叶片振动特性研究[J].中国电机工程学报, 2005, 25(18): 86-90.

Xie Yonghui, Zhang Di. Numerical model for vibration characteristic of steam turbine blade with damped shroud[J]. Proceedings of the CSEE, 2005, 25(18): 86-90.(in Chinese).

[8] 任兴民, 卢娜, 岳聪, 等. 考虑转速及碰摩的带冠涡轮叶片动力特性研究[J]. 西北工业大学学报, 2013, 31(6): 926-930.

Ren Xingmin, Lu Na, Yue Cong, et al. Dynamic characteristics of flexible shrouded blades in aero-engines[J]. Journal of Northwestern Polytechnical University, 2013, 31(6): 926-930.(in Chinese)

[9] 陈璐璐, 张大义, 文敏, 等. 带凸肩风扇叶片振动特性及设计方法研究[J]. 推进技术, 2015, 36(9): 1389-1394.

Chen Lulu, Zhang Dayi, Wen Min, et al. Dynamical effects of shrouds on fan blade vibration and its corresponding design method[J]. Journal of Propulsion Technology, 2015, 36(9): 1389-1394.(in Chinese)

[10] 郝燕平. 带摩擦阻尼叶片的动力响应和减振研究[D]. 北京: 北京航空航天大学, 2001.

Hao Yanping. Dynamic response and depressing research on blade with friction damper[D]. Beijing: Beihang University, 2001.(in Chinese)

[11] 郝燕平, 单颖春, 朱梓根. 缘板摩擦阻尼器的减振实验研究[J]. 航空动力学报, 2001, 16(1): 55-58.

Hao Yanping, Shan Yingchun, Zhu Zigen. Effects of platform friction damper on resonant stresses in gas turbine blades[J]. Journal of Aerospace Power, 2001, 16(1): 55-58.(in Chinese)

[12] 单颖春, 郝燕平, 朱梓根, 等. 干摩擦阻尼块在叶片减振方面的应用与发展[J]. 航空动力学报, 2001, 16(3): 218-223.

Shan Yingchun, Hao Yanping, Zhu Zigen. Application and development of platform friction damper for depressing resonant vibration of blades[J]. Journal of Aerospace Power, 2001, 16(3): 218-223.(in Chinese)

[13] 郝燕平, 朱梓根. 带摩擦阻尼的叶片响应求解方法[J]. 航空学报, 2001, 22(5): 411-414.

Hao Yanping, Zhu Zigen. New method to resolve vibratory response of blades with friction damping[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(5): 411-414.(in Chinese)

[14] 漆文凯. 涡轮转子叶片叶根阻尼装置减振特性分析及实验研究[D]. 南京: 南京航空航天大学, 2005.

Qi Wenkai. Vibration analysis and test research of rotating turbine blade with damper[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005.(in Chinese)

[15] 漆文凯, 高德平. 带摩擦阻尼装置系统振动响应分析方法研究[J]. 航空动力学报, 2006, 21(1): 161-167.

Qi Wenkai, Gao Deping. Study of vibration response analysis method for the dry friction damping systems[J]. Journal of Aerospace Power, 2006, 21(1): 161-167.(in Chinese)

[16] Griffin J H, Sinha A. The interaction between mistuning and friction in the forced response of bladed disk assemblie[J]. Journal of Engineering for Gas Turbines and Power, 1985, 107(1): 87.

[17] Sinha A, Griffin J H. Effects of friction dampers on aerodynamically unstable unstable rotor stages[J]. AIAA Journal, 1985, 23(2): 262-270.

[18] Wang Qinmeng, Zhang Jin, Ma Xiaoqiu, et al. Hybrid method to analyze contact stress distribution on dry friction interfaces[J]. Chinese Journal of Aeronautics, 2002, 15(2): 77-81.

[19] 张锦, 刘晓平. 叶轮机振动模态分析理论及数值方法[M]. 北京: 国防工业出版社, 2001.

Zhang Jin, Liu Xiaoping. Principle and numerical methods of modal analysis to turbomachines[M]. Beijing: National Defense Industry Press, 2001.(in Chinese)

[20] Sinha A, Griffin J H. Effects of static friction on the forced response of friction damped turbine blades[J]. Journal of Engineering for Gas Turbine and Power, 1984, 106(1): 65-69.

[21] 李剑钊, 闻雪友, 林志鸿. 汽轮机带冠叶片振动特性研究进展[J]. 汽轮机技术, 2005, 47(4): 241-247.

Li Jianzhao, Wen Xueyou, Li Zhihong. The advancement of study on vibration characteristics of shrouded blade of steam turbine[J]. Turbine Technology, 2005, 47(4): 241-247.(in Chinese)

[22] Oancea V G, Laursen T A. Investigations of low frequency stick-slip motion: experiments and numerical modeling[J]. Journal of Sound and Vibration, 1998, 213(4): 577-600.

[23] Ferri A A. Friction damping and isolation systems[J]. Transaction of the ASME, 1995, 117(6): 196-206.

[24] Sanliturk K Y, Imregun M, Ewins D J. Harmonic balance vibration analysis of turbine blades with friction dampers[J]. ASME Journal of Vibration and Acoustics, 1997, 119(1): 96-103.

[25] Meng C H, Griffin J H, Bielak J. The influence of micro-slip on vibratory response PartⅡ: A comparision with experimental results[J]. Journal of Sound and Vibration, 1986, 107(2): 295-307.

[26] Menq C H, Bielak J, Griffin J H. The influence of microslip on vibratory response. Part I: A new microslip model[J]. Journal of Sound and Vibration, 1986, 107(2): 279-293.

[27] Sanliturk K Y, Ewins D J. Modelling Two-dimensional friction contact and its application using harmonic balance method[J]. Journal of Sound and Vibration, 1996, 193(2): 511-523.

[28] 何尚文, 任兴民, 秦卫阳, 等. 基于微滑移模型的B-G型叶片缘板阻尼器减振特性研究[J]. 振动与冲击, 2012, 31(1): 44-48.

He Shangwen, Ren Xingmin, Qin Weiyang, et al. Reduced vibration characteristics of a B-G platform damper based on a micro-slip model[J]. Journal of Vibration and Shock, 2012, 31(1): 44-48.(in Chinese)

[29] 徐自力, 常东锋, 上官博. 微滑移离散模型及在干摩擦阻尼叶片振动分析中的应用[J]. 机械科学与技术, 2007, 26(10): 1304-1307.

Xu Zili, Chang Dongfeng, Shang Guanbo. One-bar microslip discrete model and its application to vibration analysis of blade with dry friction damper[J]. Mechanical Science and Technology for Aerospace Engineering, 2007, 26(10): 1304-1307.(in Chinese)

[30] 徐自力, 常东锋, 刘雅琳. 基于微滑移解析模型的干摩擦阻尼叶片稳态响应分析[J]. 振动工程学报, 2008, 21(5): 505-510．

Xu Zili, Chang Dongfeng, Liu Yalin. Forced response analysis of blade system with dry friction damper using one-bar micro slip analytic model[J]. Journal of Vibration Engineering, 2008, 21(5): 505-510.(in Chinese)

[31] 上官博, 徐自力, 肖俊峰, 等. 一种正压力随时间变化的微滑移干摩擦模型[J]. 振动工程学报, 2016, 29(3): 444-451.

Shang Guanbo, Xu Zili, Xiao Junfeng, et al. A mocro-slip dry friction model with variable normal load[J]. Journal of Vibration Engineering, 2016, 29(3): 444-451.(in Chinese)

[32] Iwan W D. On a class of models for the yielding behavior of continuous and composite system[J]. Journal of Applied Mechanics, 1967, 34(3): 612-617.

[33] Menq C H, Bielak J, Griffin J H. The influence of microslip on vibratory response, Part Ⅰ: A new micro-slip model[J]. Journal of Sound and Vibration, 1986, 107(2): 279-293.

[34] Menq C H, Griffin J H, Bielak J. The influence of microslip on vibratory response, Part Ⅱ: A comparison with experimental results[J]. Journal of Sound and Vibration, 1986, 107(2): 295-307.

[35] 漆文凯, 高德平. 带摩擦阻尼装置系统振动响应分析法研究[J]. 航空动力学报, 2006, 21(1): 167-173.

Qi Wenkai, Gao Deping. Study of vibration response analysis method for the dry friction damping systems[J]. Journal of Aerospace Power, 2006, 21(1): 167-173.(in Chinese)

[36] Yang B D, Meng C H. Characterization of 3D contact kinematics and prediction of resonant response of structures having 3D frictional constraint[J]. Journal of Sound and Vibration, 1998, 217(5): 909-925.

[37] Sanliturk K Y, Ewins D J. Modelling two dimensional friction contact and its application using harmonic balance method[J]. Journal of Sound and Vibration, 1996, 193(2): 511-523.

[38] Griffin J H. A review of friction damping of turbine blade vibration[J]. International Journal of Turbo and Jet Engines, 1990, 7(3/4): 297-308.

[39] Wang J H, Shienh W L. The influence of a variable friction coefficient on the dynamic behavior of a blade with a friction damper[J]. Journal of Sound and Vibration, 1991, 149(1): 137-145.

[40] 梁明轩, 袁惠群, 赵天宇, 等. 内燃机曲轴轴系弯扭耦合非线性振动响应[J]. 东北大学学报: 自然科学版, 2014, 35(3): 402-405.

Liang Mingxuan, Yuan Huiqun, Zhao Tianyu, et al. Response of nonlinear bending-torsional coupling vibration of the combustion engine crankshaft system[J]. Journal of Northeastern University(Natural Science), 2014, 35(3): 402-405.(in Chinese)

[41] Wang J H, Chen W H. Investigation of the vibration of a blade with friction damper by HBM[J]. Journal of Engineering for Gas Turbines and Power, 1993, 115(2): 294-299.

[42] Pierre C, Ferr A A, Dowell E H. Multi-harmonic analysis of dry friction damped systems using an incremental harmonic balance method[J].Journal of Applied Mechanics, 1985, 52(4): 958-964.

[43] Cameron T M, Griffin J H. An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic systems[J]. Journal of Applied Mechanics, 1989, 56(1): 149-154.

[44] Guillen J. Studies of the dynamics of dry-friction-damped blade assemblies[D]. Michigan: University of Michigan, 1999.

[45] Poudou O. Modeling and analysis of the dynamics of dry-friction-damped structural systems[D]. Michigan: University of Michigan, 2007.

[46] Poudou O, Pierre C. Hybrid frequency-time domain methods for the analysis of complex structural systems with dry friction damping[J]. AIAA-2003-1411, 2003.

[47] Nacivet S, Pierre C, Thouverez F, et al. A dynamic lagrangian frequency-time method for the vibrarion of dry friction-damped systems[J]. Journal of Sound and Vibration, 2001, 265(1): 201-219.

[48] Laxalde D, Thouverez F, Sinou J J, et al. Qualitative analysis of forced response of blisks with friction ring dampers[J]. European Journal of Mechanics A: Solids, 2007, 26(4): 969-978.

[49] Herzog A, Krack M. Comparison of two widely-used frequency-time contact models for the vibration Simulation of shrouted turbine blades[J]. ASME GT-2014-26226, 2014.

[50] Krack M, Herzog A, Panning S, et al. Multi harmonic analysis and design of shroud friction joints of bladed disks subject to microslip[C]∥Proceedings of the ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Chicago, USA: ASME, 2012: 1-10.

[51] 李琳, 刘久周, 李超. 干摩擦阻尼器对宽频多阶次激励减振效果分析[J]. 航空动力学报, 2016, 31(9): 2171-2180.

Li Lin, Liu Jiuzhou, Li Chao. Analysis on damping effect of dry friction damper under wideband multi-harmonic excitation[J]. Journal of Aerospace Power, 2016, 31(9): 2171-2180.(in Chinese)

[52] 何尚文, 任兴民, 康召辉, 等. 基于等效线性化法的干摩擦缘板系统振动特性研究[J]. 机械科学与技术, 2010, 29(12): 1727-1731.

He Shangwen, Ren Xingmin, Kang Zhaohui, et al. Vibration characteristics of a platform system with dry friction damper using equivalent linearization method[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(12): 1727-1731.(in Chinese)

[53] 丁千, 孙艳红. 干摩擦阻尼叶片多谐波激振的共振响应[J]. 振动与冲击, 2004, 11(1/2): 12-18.

Ding Qian, Sun Yanhong. Resonances of dry friction damper turbine blades under multi-frequencies excitation[J]. Journal of Vibration and Shock, 2004, 11(1/2): 12-18.(in Chinese)

[54] 卢娜, 任兴民, 岳聪, 等. 基于改良整体滑动模型的缘板干摩擦阻尼器减振特性研究[J]. 机械科学与技术, 2013, 32(9): 1263-1266.

Lu Na, Ren Xingmin, Yue Cong, et al. Damping characteristics of dry friction platform damper system based on improved macro-slip model[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(9): 1263-1266.(in Chinese)

[55] 张亮, 袁惠群, 韩清凯, 等. 基于微动滑移摩擦模型的失谐叶盘系统振动分析[J]. 振动工程学报, 2012, 25(3): 289-293.

Zhang Liang, Yuan Huiqun, Han Qingkai, et al. Vibration analysis of mistuned bladed disk system based on microslip friction model[J]. Journal of Vibration Engineering, 2012, 25(3): 289-293.(in Chinese)