基于Hamming窗的滤波反投影CT图像重建算法
青岛大学 于尚民
1.引言
滤波反投影(FBP,Filter Back Projection)算法是一种最为常用的CT图像重建算法。FBP算法有较低的时间复杂度,其重建图像的空间分辨率较高[1]。在反投影算法中,所有方向下的投影累加而形成重建后的图像。在累加结束后,无限空间中原本像素值为0的点的像素值变为非0。因此反投影算法重建的图像,会有明显的“星”状伪影。为了消除这种伪影,需要在重建过程中引入滤波函数[2,3]。在滤波反投影算法中,滤波函数的选择一直以来都是研究的重点,本文引入Hamming窗函数,经实验验证,Hamming窗重建图像的质量比常见的R-L滤波函数和 S-L滤波函数的更高。
2.滤波器的设计
滤波器设计的好坏会对重建图像的质量产生巨大影响。FBP算法理论上要求滤波器的系统函数,但实际上的滤波函数是一种频带宽度无限大的函数。在实际应用中,由Paley-W iener准则可知,这种理论上的滤波器是不可能实现的。但实际CT设备的分辨率有限,其收集到的投影是一种频谱能量分布于低频区域的密度分布[4]。因此可以忽略超出某个截止频率的投影数据, 即:

W( ρ)称为窗函数,其好坏对重建图像质量起着关键性作用。因此要求窗函数W( ρ)应遵守以下原则:
(1)主瓣宽度要窄,以增大图像分辨率;
(2)最大旁瓣尽可能的要小,以减弱吉布斯现象。
3.Hamming滤波函数
3.1 Hamming窗函数性质分析
Hamming窗是一种常见的窗函数,其频率响应表达式为:

其脉冲响应函数:

Hamming窗也是余弦窗的一种,又称改进的升余弦窗。Hamming窗与Hanning窗都是余弦窗,只是加权系数不同。Hamming窗加权的系数能使旁瓣达到更小。
各窗函数的主瓣频宽(其中N为窗函数长度)和第一旁瓣衰减值如表1所列。

表1 主瓣频宽与第一旁瓣相对主瓣衰减值
3.2 Hamming窗函数实验结果分析
为了对Hamming窗函数重建图像的质量进行检验,实验中采用了经典的Shepp-Logan模型进行平行束滤波反投影重建。Shepp-Logan模型的投影数据为512* 512,重建图像的大小为514*514,结果如图1所示。

图1 三种滤波函数的重建结果
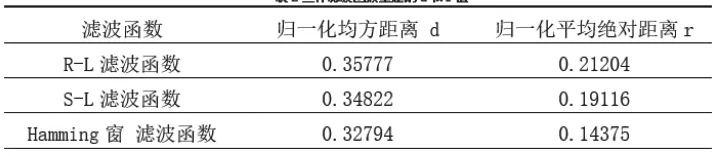
表2 三种滤波函数重建的d和r值
实际CT成像中常常会有噪声出现。因此,本文引入了泊松噪声来对Hamming窗的重建结果进行分析。

改变参数λ,就可以改变产生泊松噪声的大小。在噪声测试中λ的取值分别为0.1,1,2,其重建图像和误差分析分别如图2、表3所示。
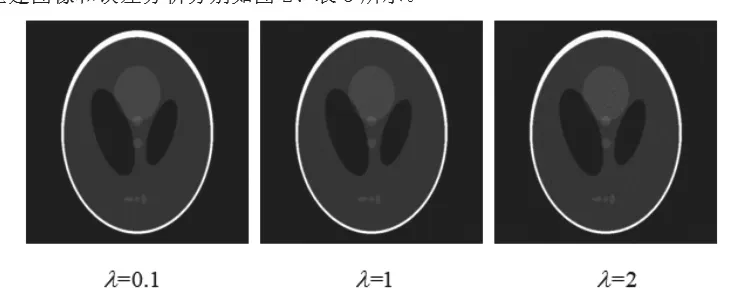
图2 Hamming窗滤波函数在泊松噪声下的重建结果

表3 Hamming窗滤波函数在泊松噪声下的重建图像d和r值
由图2和表3可以看出,Hamming窗滤波函数在泊松噪声下仍然可以获得较高质量的图像。
4.结束语
本文通过对Hamming窗滤波函数重建图像的分析,证实了其归一化均方距离和归一化绝对距离均较小,图像重建效果比常用的R-L、S-L滤波函数更好。此外本文还分析了泊松噪声对Hamming窗滤波函数重建图像的影响,验证了Hamming窗的抗噪能力,证实了Hamming窗的优越性。
[1]骆岩红.CT图像重建滤波反投影算法中指数滤波器的研究[J].计算机科学,2014,41(S1):220-223.
[2]乔志伟.高速高精度解析式图像重建算法研究[D].北京交通大学,2011.
[3]王珏,黄苏红,蔡玉芳.工业CT图像环形伪影校正[J].光学精密工程,2010,18(05):1226-1233.
[4]马晨欣.CT图像重建关键技术研究[D].解放军信息工程大学,2011.
[5]蔚慧甜.基于汉宁窗函数的滤波器的设计[J].传感器世界,2011,17(12):27-29.
[6]张斌,潘晋孝.CT图像重建的新型混合滤波器[J].微计算机信息,2009,25(09):298-299+308.

