基于改进差分进化算法的磁流变阻尼器建模研究

武汉理工大学自动化学院 刘 冰 傅 剑

0 引言

汽车行驶时，由于路面的高低不平，车身会受到冲击发生振动。轻微的车身振动会影响车载人员的舒适性，但较大的振动不仅会损坏汽车零件，严重时还会影响车载人员的安全。在现代汽车结构中主要是通过车辆悬架系统来减缓振动，保证车辆的行驶的平顺性和操纵的稳定性。

基于磁流变阻尼器的半主动悬架利用磁流变液受外加磁场作用其流变特性发生改变的特点，使得悬架能在较大范围内，较低功耗下实现阻尼可调，从而满足汽车变路面、变工况的需要。现有研究表明，该悬架对车辆的驾驶平顺性和操纵稳定性有显著改善，是下一代智能悬架的发展方向，具有巨大的研究价值和广阔的应用前景[1]。

现阶段磁流变半主动悬架的主要技术难点之一在于磁流变阻尼器的力学特性具有较为复杂的迟滞非线性，常规的工程方法难以建立符合实际应用需求的数学模型,国内外相关学者对此问题进行了大量研究。本课题拟基于对磁流变阻尼器力学试验数据的分析，构建出准确高效，便于控制阻尼器数学模型。

1 磁流变阻尼器力学试验分析

本文试验对象为武汉理工大学自行设计的磁流变阻尼器，如图1所示。力学试验中，电机驱动阻尼器活塞杆相对于阻尼器缸筒做简谐运动。设置激励输入频率为1Hz，幅值为0.03m。分别测得磁流变阻尼器在不同励磁线圈电流下的F-v和F-s的数据，对数据进行处理后绘制出相应关系曲线，如图2所示。

图1 磁流变阻尼器实物图

对外特性曲线进行分析，可将磁流变阻尼器阻尼力的变化过程分为四个阶段，具体如下：

在阻尼器活塞位移由正向最大位置运动至0阶段，同时速度也由0增大到负向最大，在此阶段阻尼器阻尼力先随速度变化迅速负向增大后再转为近似线性增大，原理是被低速剪切时，磁流变液存在屈服应力，而当剪切速率提高，超过其剪切屈服强度时磁流变液则表现为有固定屈服强度的牛顿流体特征，但由于剪切稀化现象存在，阻尼力并非呈现严格的线性增大。

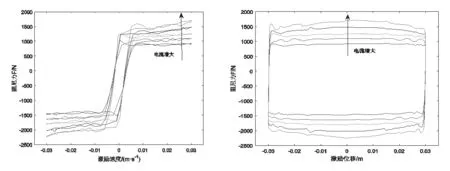
图2 磁流变阻尼器随电流变化的外特性曲线图

图3 Bouc-wen模型示意图

在阻尼器活塞位移由0运动至负向最大位置以及位移由负向最大位置至0的过程与上述分析类似。

考虑励磁线圈电流与磁流变阻尼器输出阻尼力的关系。当线圈电流增大时，阻尼器内的磁场强度随之增强，磁流变液的剪切屈服强度也会提高，在未屈服阶段磁流变阻尼器输出的阻尼力也越大，造成迟滞回环也越大。而在因电流增大磁场强度快达到上限时，磁流变液屈服强度增大减缓，阻尼器输出阻尼力增加幅度不明显，接近饱和。

2 磁流变阻尼器参数模型

Bouc-wen模型是1976年Wen[2]用于拟合力学特性曲线使其光滑过渡首次提出的，该模型特别适用于具有非线性滞回特性的磁流变阻尼器。其结构如图3所示。

Bouc-wen模型描述的磁流变阻尼器力学模型公式如下：

上式中，为磁流变液屈服后的粘性系数；为激励速度；为弹簧元件初始位移；为滞变力相关参数；为滞变位移；为曲线圆滑系数；均为迟滞环相关的系数，难以用具体物理量描述。

由于Bouc-wen模型公式相对简单，涉及的参数也相对较少，特别是描述阻尼器的力-位移和速度-位移关系曲线特别精确，因此本文选择Bouc-wen模型作为前文中的磁流变阻尼器的对象模型，其模型参数可用参数识别的式确定。

取剪跨比λ为4，轴压比ηk为0.1，配筋率ρl为0.96%在不同纵筋强度的三种矩形空心墩，纵筋强度分别为464 MPa、507 MPa、542 MPa，进行Pushover分析，其对应的能力曲线如图12所示，由图12可知，纵筋强度的提高对空心墩的承载能力有所提高，但空心墩位移延性随着纵筋强度的提高而减小。

3 磁流变阻尼器建模

参数识别是一种利用实验数据确定理论模型参数的方法。本文对磁流变阻尼器建模主要思路是，遵循一定约束条件，通过智能算法对阻尼器试验数据进行处理，计算出最为吻合试验数据的模型中的参数。

3.1 差分进化算法及其改进

差分进化算法(Differential Evolution)，简称DE算法，是1996年由Storn和Price最初为解决Chebyshev多项式而提出的[3]。和其他进化算法相比差分进化算法在求解高维、多极值、非线性复杂函数时鲁棒性、计算速度和全局搜索能力上有明显的优势。

基本的DE算法虽然求解能力很强，但是仍有值得完善的地方：随着迭代次数的增加，种群的多样性变小，过早收敛于局部最优点。为平衡全局搜索和局部搜索能力，可以通过对控制参数的调整来对DE算法进行改进。为此本文在DE算法的一些参数上引入自适应调整策略，以使DE算法更好的适用于Bouc-wen模型的参数识别。

(1)变异操作的改进

变异过程中的缩放因子用于控制差分向量对变异个体影响程度，在标准DE算法中，合适的F值不易由公式求得准确值，一般根据经验选取一个0到2之间的固定实数。自适应变异算子λ的引入是对DE算法进行改进的常用方法，它的作用是在算法执行过程中自适应调整种群变异扰动[4]。F可以用如下公式表述：

式中，F0是缩放常数；G是最大迭代次数；g是当前迭代代数。由上式可以看出，在迭代开始时，缩放因子F = 2F0，使种群在初期有较大个体差异性，避免早熟，算法具有较强的全局搜索能力；随着迭代次数增加，F逐渐减小，到迭代后期F值接近F0，这种策略使优良个体信息得以保留，提高了求解精度。

(2)交叉操作的改进

DE算法中，交叉概率CR值决定了变异中间个体与原个体之间信息交换的比例，对算法的收敛速度和种群多样性也有关键影响。CR取值对算法执行的影响不易直接观察得到，一般认为种群多样性较好时，较小的CR值使新个体中变异信息较少，增强了全局搜索能力，提高了求取最优解的概率；反之，种群多样性较差时，较大的CR值提高了新个体中变异信息的比例，增大了种群多样性，加快了收敛速度，对CR值引入自适应调整的策略。CR值可表示如下：

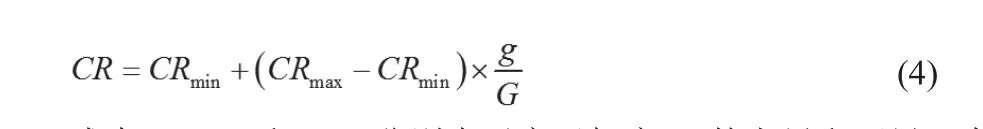
式中，CRmax和CRmin分别表示交叉概率CR的上界和下界。在初始阶段，CR值较小，此时收敛速度较慢，能让算法具有较强的全局搜索能力。随着迭代次数增加，CR值也开始增加收敛速度也逐渐加快，到后期人为增加了物种多样性，提高了算法的求解精度。

3.2 Bouc-wen参数识别

参数识别的实施策略是，将DE算法的每个个体作为模型需要识别参数的一组解，选取由模型计算出的阻尼力与试验数据差值的平方和作为适应度函数，通过DE算法迭代更新，搜索出适应度最低的一组解。

在Bouc-wen模型中，n为与曲线圆滑度相关的系数，一般值为2。为弹簧元件初始位移，在本文中为0。则需要识别的参数共6个，分别是。

对DE算法参数进行设置。取初始种群个数NP = 100；最大迭代次数G = 500；变异参数F0=0.3；交叉概率CRmax= 0.85，CRmin。由于参数范围难以直接确定，首次识别时取较大取值范围，因此可设：

式中，m为采样点个数，F为由Bouc-wen模型计算得出的阻尼力，Ft为采样点实际阻尼力。

利用磁流变阻尼器力学特性试验数据，对Bouc-wen模型进行改进DE算法的参数识别。其编程设计流程如图4所示。

定义参数识别的适应度函数：

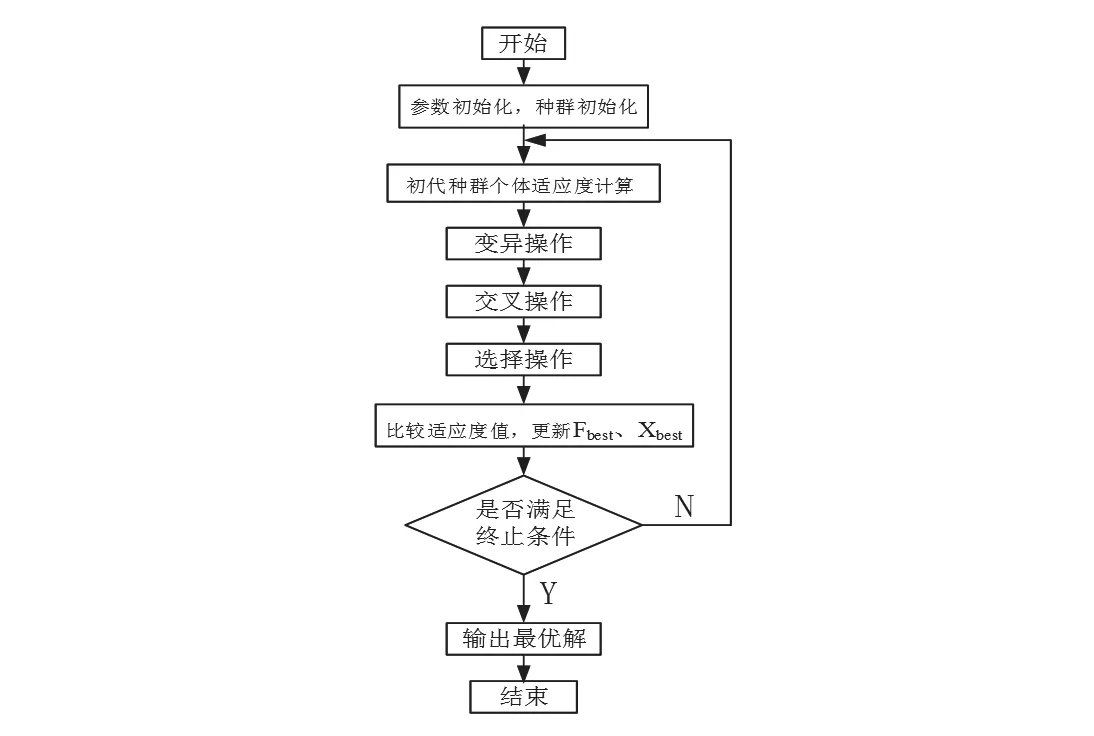
图4 改进DE算法参数辨识流程图

经过多次识别后得到的在不同电流条件下对应的各参数值，如表1所示。

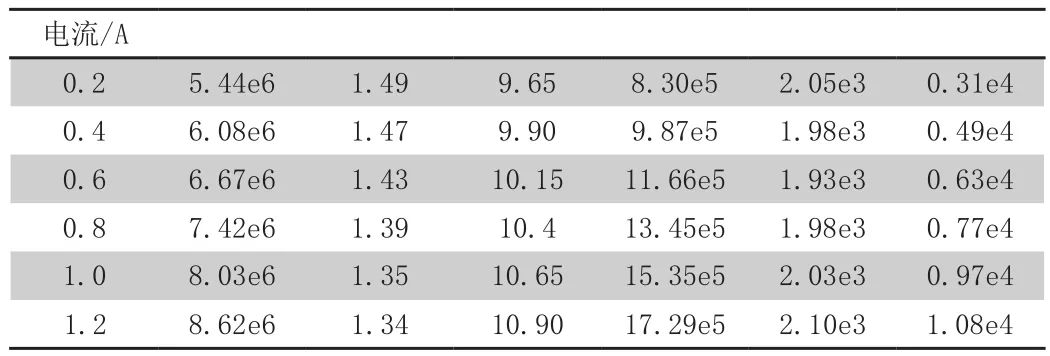
表1 DE算法识别得到的各参数值

图5 磁流变阻尼器Simulink模型

图6 仿真模型输出曲线与试验数据曲线对比

5 仿真模型及结果分析

利用所识别出的Bouc-wen模型参数，在Matlab/Simulink平台上对磁流变阻尼器进行建模，并验证仿真模型的准确性。所得模型如图5所示。

在上述模型中给定输入电流0.6A，设定位移激励为幅值为0.04m，频率为1Hz的正弦波，与相同条件下得到的阻尼器试验数据进行对比，结果如图6所示。

对比仿真模型输出结果与试验数据，可以看出，二者吻合程度很高，证明了仿真模型具有较高的精确度，达到了预期的效果。

6 结论

本文针对磁流变阻尼器建模问题，采用改进的差分进化算法，对磁流变阻尼器进行以Bouc-wen模型为对象模型的参数识别，并建立了磁流变阻尼器的仿真模型。对比仿真模型结果与实际试验数据，证明了该仿真模型精确度较高，易于控制，满足预期要求，具有较大的研究价值。

[1]王其东,梅雪晴.汽车半主动悬架的研究现状和发展趋势[J].合肥工业大学学报(自然科学版),2013(11)：1289-1294.

[2]Wen Y K.Method for Random Vibration of Hysteretic System[J].Journal of the Engineering Mechanics Division,1976,102(2)：249-263.

[3]Storn R,Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of global optimization,1997,11(4)：341-359.

[4]颜学峰,余娟,钱锋,等.基于改进差分进化算法的超临界水氧化动力学参数估计[J].华东理工大学学报(自然科学版),2006,32(1)：94-97.