闽北湿地松材积生长率表的研制
倪伟星
(福建省武夷山市林业局,福建 武夷山 354300)
森林采伐限额管理是保证森林资源可持续利用的一项重要措施,而准确的森林生长量估测值是确定管理采伐限额的重要依据[1]。长期林业生产实践表明,以胸径和年龄为辅助变量,建立材积生长率预估模型,编制材积生长率表,是确定森林生长量的一种较好的方法[2-3]。鉴于目前闽北地区尚缺乏适用湿地松的生长量表,通过收集资料,编制湿地松材积生长率表,为生产应用提供科学依据。
材积生长率表包括单木材积生长率表和林分材积生长率表,其中单木材积生长率表为森林生长量的预估提供了客观依据,但它需要通过调查取得现实林分各径阶的株数和材积来实现,不适用于只具备林分平均因子(如平均胸径、平均年龄)和蓄积量的情况下预估生长量。所以本次在研编单木材积生长率表的基础上,以林分总体为建模的基本单位,进一步探索以林分总体特征因子为辅助变量来建立林分蓄积生长率模型的建模方法,并编制林分材积生长率表,为森林资源档案管理中小班生长量预测和数据更新提供科学依据。
1 材料与数据处理
1.1 研究材料
在福建省南平延平区、政和县、武夷山等地选择郁闭度0.4以上且生长正常的湿地松,采集临时样地、固定样地以及伐区调查设计数据,样地面积为0.067 hm2,形状为矩形。共采集了不同年龄和立地质量等级的样地259块,固定样地测定次数2~5次,年龄范围为10~58 a。样地最小胸径为5 cm,最大胸径为37.1 cm,最小树高1.5 m,最大树高31.2 m,最小林分蓄积28.4 m3/hm-2,最大林分蓄积356.0 m3/hm-2,平均株数2242株/hm-2。
样地每木检尺后,取1~3棵不同胸径的湿地松,有些是样地的优势木,将样木伐倒并按1 m为一个区分段,材积其树高(H)、带皮胸径(D)、去皮胸径、每个区分段中央带皮和去皮直径及梢头木底直径,并按H的9/10、8/10、7/10、6/10、5/10、4/10、3/10、2/10、1/10,采 集样木年龄(t),并收集以往采伐数据,共收集湿地松样木有277棵,其中10 cm以下的38株,12~20 cm的87 株,22~30cm 的 90 株,32~40 cm 的 31 株,42~50 cm的22株,52以上的9株。
1.2 单木数据预处理
根据树干解析材料,以每个龄阶相邻二次观测值作为一样本单元,按复利公式计算每个样本单元的材积生长率[4]:

式中:Pν为材积生长率,νa为期初单株材积,νb为期末单株材积,n为间隔期。
按(1)式计算每个样本单元的材积生长率,并分别绘制材各生长率随直径和年龄的相关散点图,对存在异常情况的个别样本单元予以剔除,这样,经过整理后用于建模的样本单元共计272个。
1.3 林分数据预处理
依据样地每木检尺资料,求得样地各径阶株数及径阶材积。将年龄和径阶中值代入单木材积生长率模型中,求出各径阶材积生长率,乘以相应径阶的材积即得各径阶材积生长量,累加后为样地蓄积生长量,再除以样地蓄积量,求得样地蓄积生长率。以样地蓄积生长率为因变量,林分特征因子为辅助变量,建立林分蓄积生长率模型。
林分平均胸径和年龄是森林资源清查中必测的基本因子,与林分材积生长率紧密相关,尤以年龄的影响更为显著(实质上,胸径已内含有年龄的因素)。对于年龄相同的林分,立地条件好的平均胸径必然大于立地条件差的平均胸径,小密度林分的平均胸径必然大于大密度林分的平均胸径;而当平均胸径相同时,立地条件好的林分年龄必然小于立地条件差的林分年龄,小密度林分年龄必然小于大密度的林分年龄。因此,林分年龄和平均胸径可以综合反映出立地条件和林分密度不同对林分材积生长率的影响。基于此,选择林分年龄和平均胸径为辅助变量,来建立林分材积生长率模型。
2 编表模型与方法
材积生长率随直径和年龄增加而下降,通常显现反“丁”型或负指数型。为寻找最优的二元材积生长模型,我们选择了多个模型进行拟合对比,以相关指数、剩余标准差、总相对误差、平均系统误差、平均相对误差绝对值、预估数度为主要指标,对每个模型进行综合评定,最后确定湿地松最优级材积生长率模型,备选模型见式(2)~式(18)。数据均在Excel中处理。


式中:Pv为材积生长率;D 为胸径;b0、b1、b2、b3、b4为待求参数。
3 研制结果
3.1 单木材积生长率的研制
3.1.1 最优模型的选择
根据建模的样本单元,利用最小二乘法,经过计算机运算,求得各模型参数见下表。

表1 模型参数Table 1 Model parameter
利用相关指数、剩余标准差、总相对误差、平均系统误差、平均相对误差绝对值、预估精度等6个评价指标对拟合的17个方程进行评价,评价结果见下表。
从表4-14中,各评价指标各有好坏,为科学地选择出拟合效果较好的方程,现利用TOPSIS分析法进行综合评价[5],具体评价结果见下表。
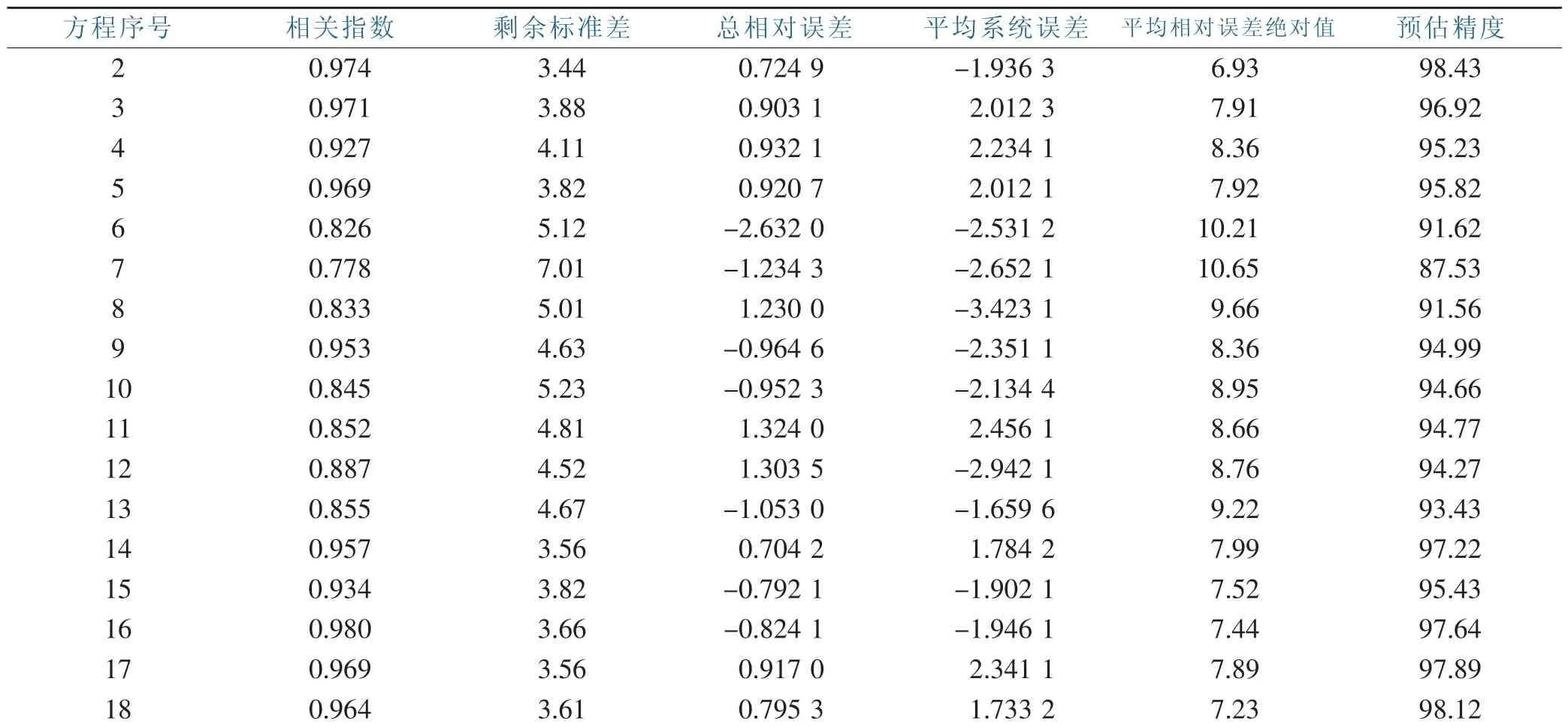
表2 模型评价结合Table 2 Model evaluation combination

表3 TOPSIS法评价结果Table 3 Evaluation results of TOPSISmethod
一个理想的材积生长率模型,除了要具有良好的拟合效果外,还应尽量简捷,且参数最好具有生物学意义。通过TOPSIS分析法综合评价结果来看,式(2)的效果是较为理想的,与二元材积模型山本式具有相同的结构形式,反映了材积生长率随着年龄和直径增加而逐渐减少,最终趋近于零的变化规律。这种变化规律符合树木生长的生物学特性,且模型简单,便于实际应用。采用逐步回归法所求的材积生长率模型,虽然相关指数要略高于山本式,但从其他各个评价指标来看,并没有显示出明显的优越性,且模型较之山本式复杂,故不予采用。根据上述分析,我们选择模型Pν=atbDc编制湿地松单株木材积生长率表。
3.1.2 模型优化与编表
为提高模型拟合精度,本次采用改进单纯形法对求解模型参数。用改进单纯形法优化材积生长率模型中的参数[6],则试验优化的因素就是方程中的各个参数,目标函数是材积生长率的理论值和实际值的残差平方和Q[7],要求目标函数值越小越好,即,

现将式(2)作为材积生长率模型,以最小二乘法所求3个参数作为初始值,应用改进单纯形法对式(2)作进一步的优化,求得材积生长率模型为:
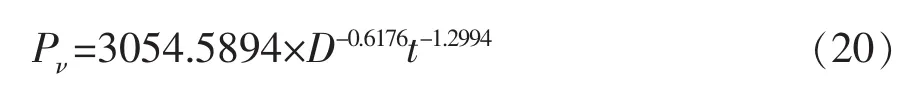
材积生长率残差平方和329.68,剩余标准差2.46。与优化前残差平方和412.55,剩余标准差3.44相比都下降,说明拟合精度有进一步提高。
为说明本次所建立的湿地松材积生长率模型适用,用未参加建模的55株样本,对优化后的材积生长率模型进行适用性检验,检验指标包括置信椭圆F检验、总相对误差、平均系统误差、平均相对误差绝对值、预估精度等5个。检验结果为,置信椭圆F=2.46[小于 F0.05(2,55)=3.17],总相对误 0.914%,平均系统误差1.787%,平均相对误差绝对值6.084%,预估精度98.55%。
通过检验说明,本次所建立的材积生长率模型适用,其误差较小,精度较高,可在林业生产实践上应用。据此,把材积生长模型按年龄和胸径展开,编成湿地松材积生长率表,具体见下表。
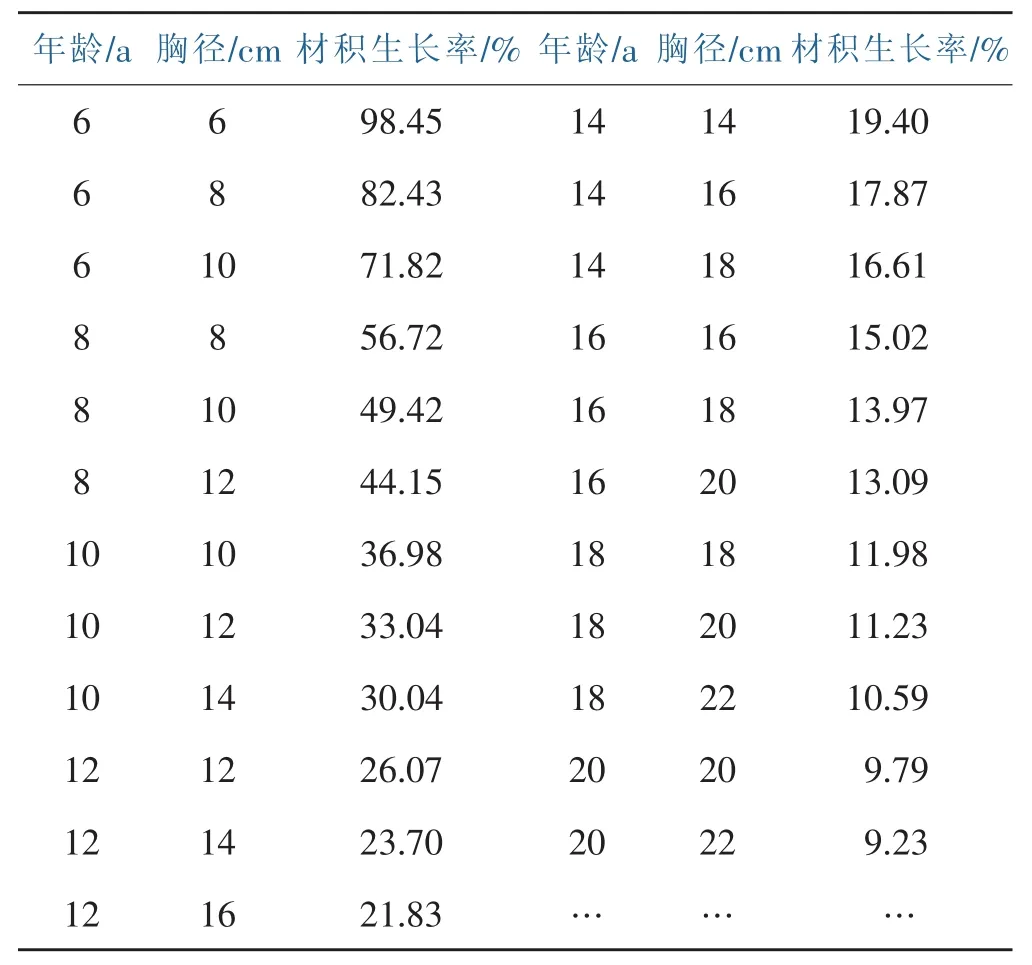
表4 湿地松单株材积生长率表Table 4 Single tree volume growth rate table of Pinus elliottii
3.2 林分材积生长率表的研制
与单木材积生长率的变化规律一样,林分材积生长率同样随林分平均胸径和年龄的增大而减少,呈“厂”型或负指数型曲线。通过对多个方程的分析对比,以下式模型效果较为理想:

式中:Pm为林分材积生长率;t为林分年龄为林分平均胸径;a0,b1,b2为参数。
用样地材料对上式进行拟合,求得各参数和统计指标为:a0=2903.5870,b1=1.4932,b2=0.4077,相关指数0.961,剩余标准差2.7681。
式(2)拟合结果表明,对湿地松林分材积生长率的变化规律有较高的切合性能,故将其作为基本模型,但上式中的b1和b2对不同的林分年龄和平均胸径的取值是固定的,即对不同的材积生长率的变化率只取一个平均变化率予以代替。如果林分材积生长率模型中的参数b1和b2不随林分年龄的变化而发生改变,采用上式是适宜的。假如b1和b2随林分年龄的变化而发生相应的改变,则采用上式直接进行拟合,则欠妥。此时应将固定参数模型改为可变参数模型,从而提高模型的预估精度。基于这一想法,本研究将式(2)设计为可变参数形式,其通式为:

式(2)称为可变参数林分材积生长率模型,建模方法如下:以前述求解结果为基础,保持a0=2903.5870不变,分别龄阶和径阶去拟合式(23)。
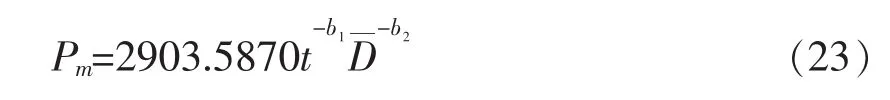
解出的参数 b1、b2列于表 5、表 6。
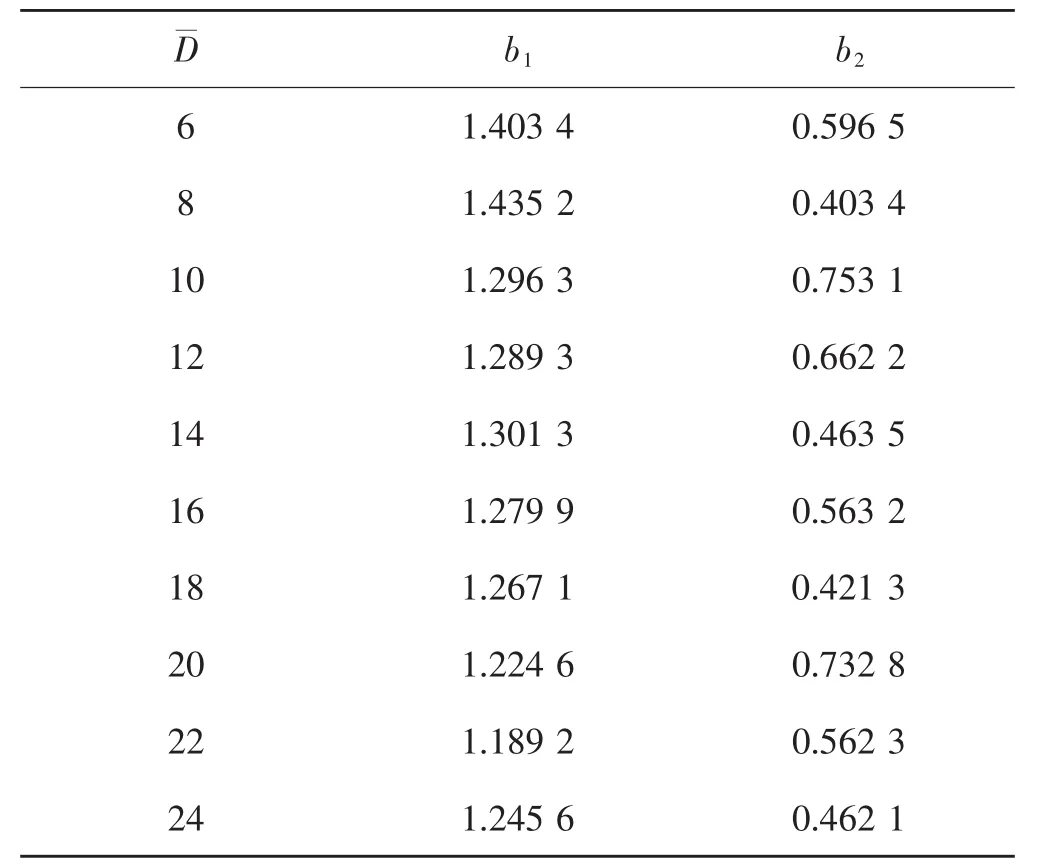
表5 不同径阶的参数b1、b2值Table 5 Parameters b1 and b2 of different sizes

表6 不同龄阶的参数b1、b2值Table 6 Parameters b1 and b2 of different age order
通过对表5和表6分别作散点图后发现,b1与平均胸径呈线性相关而与林分年龄基本无关,b2与林分年龄呈线性相关而与平均胸径基本无关。拟合b1与D、b2与t的模型为:
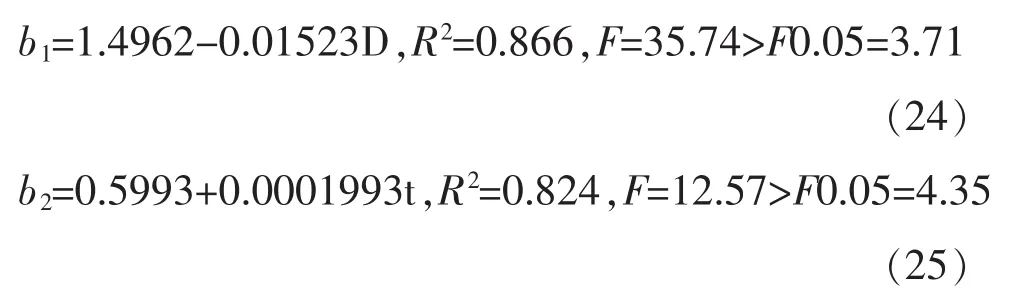
上述二个方程经过F检验,都达到极显著水平,表明林分材积生长率方程中的参数b1、b2并非是某一固定常数,而是分别随着林分平均胸径和年龄而变化而发生相关的变化。据此,可将湿地松林分材积生长率模型的可变参数形式确定为:

以 a0=2903.5870,a1=1.4962,a2=0.01523,a3=0.5993,a4=0.0001993为初值,林分材积生长率的实际值和理论值的残差平方和最小为目标函数,采用改进单纯形法对上式进行优化求解,得到如下的湿地松林分可变参数林分生长率模型:
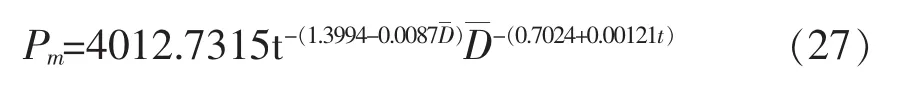
同样,为说明其适用性和精度情况,用未参加建模的62块样地,对可变参数林分材积生长率模型进行适用性检验,检验指标包括置信椭圆F检验、总相对误差、平均系统误差、平均相对误差绝对值、预估精度等5个。检验结果为,置信椭圆F=1.52[小于F0.05(2,60)=3.15],总相对误差1.429%,平均系统误差2.178%,平均相对误差绝对值7.561%,预优精度94.38%。
通过适用性检验结果表明,本次建立的可变参数林分材积生长率模型适用,其误差较小,精度较高,可在森林资源小班档案更新应用。现以林分年龄和平均胸径为辅助变量,将式(27)展开成湿地松林分材积生长率表,具体见下表。
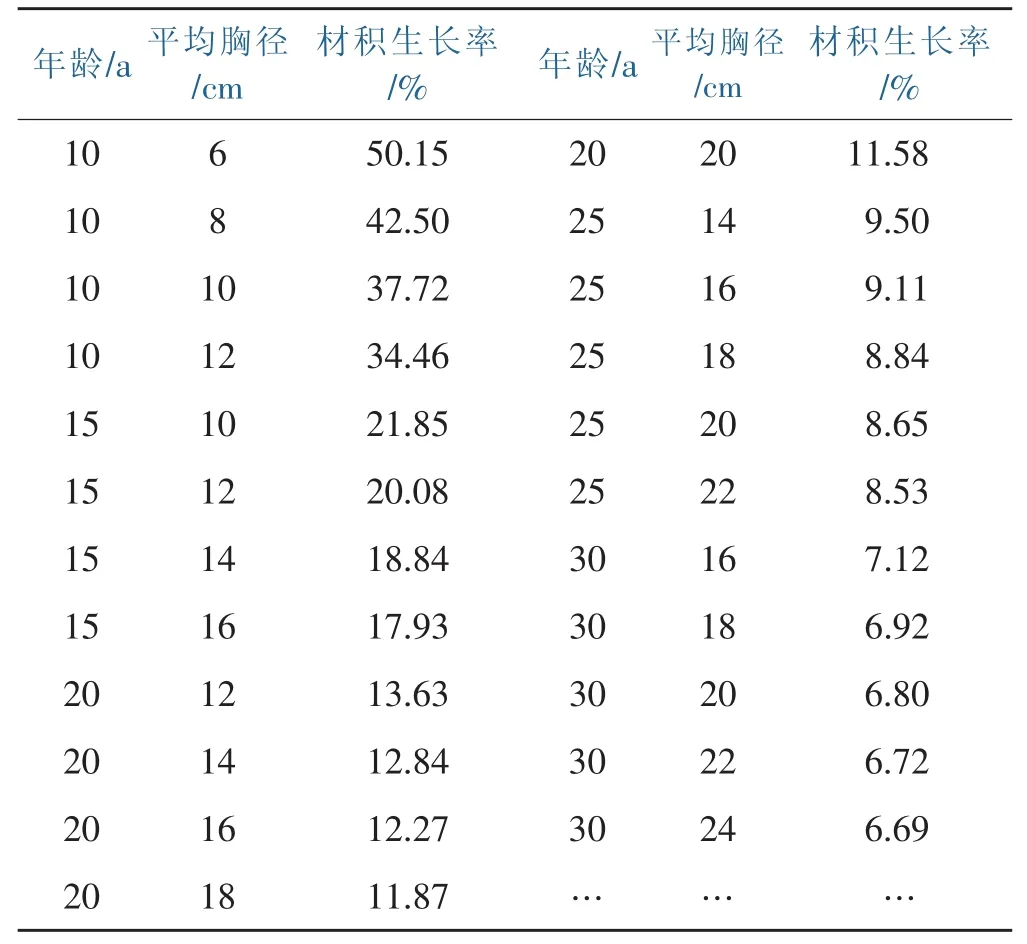
表7 湿地松林分材积生长率表Table 7 Growth rate table for the split volume of Pinus elliottii
4 结论
编制材积生长率表是确定森林生长量的一种较好的方法。鉴于闽北目前尚缺乏适用湿地松的生长量,通过收集样地、样木材料,选取17个模型作为编制湿地松单木材积生长率表的备选方程,通过TOPSIS法拟合精度对比分析,得到山本式的模型较优。
为进一步提高精度,采用改进单纯形法求解方程参数,建立了湿地松单木材积生长率方程。但在只具备林分平均因子(如平均胸径、平均年龄)和蓄积量的情况下预估生长量,单木材积生长率方程不适合。本文通过对固定参数模型改为可变参数模型,得到可变参数林分材积生长率模型,采用改进单纯形法对进行优化求解,得到如下的湿地松林分可变参数林分生长率模型,编制了湿地松材积生长表,为生产应用提供科学依据。
[1]程光明.杉木人工林材积生长率表编制的研究[J].福建林业科技,2006(3):56-59.
[2]曾小波.闽东杉木人工林材积生长率表的编制[J].林业勘察设计,2000(2):10-13.
[3]陈文雄.连江县湿地松人工林单木材积生长率表的研制[J].林业勘察设计,2012,64(2):5-8.
[4]黄修麟.尤溪国有林场杉木人工林单木材积生长率表编制研究[J].林业勘察设计,2010,60(2):8-11.
[5]华伟平,丘甜,盖新敏,等.基于交叉建模检验的黄山松二元材积模型建模技术[J].武夷学院学报,2015,34(6):13-17.
[6]江希钿.单木模型的研制及优化的研究[J].中南林业调查规划,1996(1):1-4.
[7]施恭明,江希钿,陈绍玲,等.福建省马尾松多形地位指数曲线模型的研究[J].林业勘察设计,2015,70(2):1-4.

