海南省桉树生长率模型研建
周湘红,贾 嘉,陈振雄
(1.国家林业局中南林业调查规划设计院,长沙410014; 2.怀化市林业调查设计院,湖南 怀化 418000)
海南省桉树生长率模型研建
周湘红1,贾 嘉2,陈振雄1
(1.国家林业局中南林业调查规划设计院,长沙410014; 2.怀化市林业调查设计院,湖南 怀化 418000)
利用海南省1998年、2003年和2008年森林资源连续清查中,复查的3642株桉树保留木、135个桉树实测样地资料,研究建立了桉树胸径生长率、材积生长率和林分材积生长率模型。所建模型拟合效果良好,无明显系统偏差,建立的桉树胸径生长率模型预估精度达96%以上,一元、二元林分材积生长率模型预估精度均在99%以上,可为以后海南省开展各类森林资源调查估算桉树生长量提供参考依据。
桉树;生长率;森林资源清查;方程;海南省
材积生长率模型不仅是进行确定森林生长量最有效的方法,同时也是确定森林采伐限额的重要依据[1],在我国的森林资源清查工作中,材积生长率模型还直接作为复查时判定胸径测量值是否正常的手段[2]。长期实践表明,编制材积生长率模型可以更好地发挥森林资源调查成果的作用,为及时更新森林资源档案、准确掌握森林资源动态变化、确保森林资源档案管理的科学性、时效性和连续性等方面具有十分重要的意义。海南省自1988年成立以来,由于受多方面因素影响,一直未建立桉树材积生长率模型[3]。根据2013年海南省森林资源清查[4],桉树林面积14.62万hm2,占全省人工乔木林面积的31.9%,作为海南省主要的人工造林树种,研究建立其生长率模型是十分迫切和非常必要的。
1 数据来源与处理
1.1 数据来源
桉树生长率模型研建所用资料来自海南省1998年、2003年和2008年森林资源连续清查中复查的实测样地和2011年海南省桉树常用数表研建项目外业调查样地。剔除森林资源清查样地中采伐木、枯死木、多测木和胸径错测木,其余剩下的(以下称保留木)样地桉树样木即为研建胸径生长率模型的基础资料,共选取桉树保留木3642株,最小胸径5.0 cm,最大胸径42.8 cm;选取优势树种为桉树的样地135个,其中幼龄林、中龄林、近熟林、成熟林样地约30个,过熟林样地15个,来建立林分材积生长率模型。
1.2 数据处理
由于选取的部分样木在清查样地林分中可能不占优势,或为散生木(四旁树),每株样木的年龄不能全部采用样地林分平均年龄来代替。考虑到胸径与年龄之间一般存在着高度的相关关系,因此,建立胸径生长率模型只采用胸径作为自变量。
首先利用保留木的前后期胸径数据,按复利式计算胸径生长率[5]:
PD=[(D2/D1)1/n-1]×100
(1)
式中PD为胸径生长率、D1为前期胸径、D2为后期胸径、n为复测间隔期。
根据计算得到的生长率分径阶(1 cm间距)用3倍标准差剔除特别异常的样木,并绘制胸径生长率PD与前期胸径D1的散点图(图1),根据散点图再次剔除数据异常的样木。

图1 桉树胸径生长率与胸径的散点分布图
由于各树种样木随径阶分布不均,为了减少对模型参数估计的影响,此处采用平均数建模方法,即:首先1 cm间距计算平均胸径和平均生长率,然后再根据平均胸径和平均生长率的成对值拟合模型。
2 模型构建
2.1 胸径生长率模型结构
建立以胸径为自变量的一元胸径生长率模型。从图1可以看出,胸径生长率与胸径的关系大体呈反“J”型曲线,这类曲线一般可以用幂函数等表示。通过对自变量和因变量作倒数、对数等变换后进行分析还发现,桉树胸径生长率与胸径的倒数大体呈线性相关。因此,胸径生长率模型确定采用以下结构形式[2]:
PD=c0+c1/D
(2)
式中D为胸径、PD为胸径生长率、c0和c1为参数。
2.2 林分材积生长率模型结构
为方便在实际生产中应用,在单木材积生长率模型的基础上进一步编制林分材积生长率模型。选取上述桉树占优势的样地,将每个样地的所有活立木按单木生长率模型推算期末样地蓄积量,但不考虑进界生长及自然枯损与采伐消耗,再以每个样地为样本单元,建立林分材积生长率与林分平均直径的一元模型,或建立林分材积生长率与林分平均直径和林龄(A)的二元模型。根据林分材积生长率呈反“J”形曲线的变化规律,设计模型结构如下[1]:
林分材积生长率二元模型:
Pv=C0D-C1A-C2
(3)
林分材积生长率一元模型:
Pv=C0D-C1
(4)
式中Pv为林分材积生长率,D为胸径,A为林分年龄,Ci为参数。
2.3 模型检验评价
检验评价指标如下:确定系数(R2)、平均预估精度(P)、估计值的标准误差(SEE)、平均百分标准误差(MPSE)、总相对偏差(TRB)和平均系统偏差(MSB)。计算公式[6-7]式(5)~式(9):

(5)
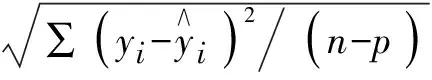
(6)
(7)
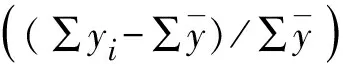
(8)

(9)

R2和SEE是回归模型评价的常用指标,P可视为总体水平上平均估计值的精度指标,TRB和MSB是反映方程总体拟合效果的重要指标。对拟合效果好的模型,同时要求其参数稳定,即参数估计值的t值大于2或变动系数小于 50%[8];建立的模型一般还须进行残差随机分布检验,残差应均匀对称随机分布,即各阶径的残差正负相抵,以 0 为基准线上下对称分布。
3 拟合结果
3.1 胸径生长率模型
利用建模数据,采用非线性加权回归估计方法进行拟合,权函数采用模型本身的倒数,建立的胸径生长率模型见表1。可以看出,建立的胸径生长率模型确定系数(R2)和平均预估精度(P)分别为0.925 7和96.28%,模型拟合效果良好。

表1 桉树胸径生长率模型拟合结果模型参数估计值变动系数/%统计指标c0c1c0c1R2SEERSSP/%TRB/%MSB/%(2)1 9653433 816399 35 080 92570 538 5496 280 851 41
3.2 材积生长率模型
由于在森林资源连续清查中对材积的估计全部采用了以下形式的一元立木材积模型:V=a·Db(D为胸径),因此,根据材积与胸径的关系可以导算出材积生长率与胸径生长率之间的关系式,具体为:

(10)
式中b为一元材积模型的参数。将前面胸径生长率模型及一元材积模型参数代入(5)式,直接得到桉树材积生长率模型:
3.3 林分材积生长率模型
采用非线性加权回归估计方法进行模型拟合,以模型本身的倒数为权函数。得到桉树林分材积生长率模型拟合结果见表2。

表2 桉树林分材积生长率模型拟合结果模型参数估计值变动系数/%统计指标C0C1C2C0C1C2R2SEERSSP/%TRB/%MSB/%(3)65 685950 714550 01161 561 1228 820 98740 269 290 013-0 00199 69(4)66 376350 72729/1 581 01/0 98680 2710 100 01399 68
从表2中可以看出,无论一元、二元林分材积生长率模型,R2均在0.98以上,TRB整体指标值接近等于0,MSB的整体指标值为0,P均在99.0%以上,模型拟合效果好。为进一步分析模型的残差是否随机,作出林分材积生长率残差随林分平均胸径变化的残差分布图进行分析、检验。从图2中可以看出,桉树的一元或二元林分材积生长率模型的残差呈随机分布,不存在明显的系统偏差。
4 结论与讨论
1) 桉树一元和二元林分材积生长率模型复相关系数在0.98以上,相关紧密。
2) 桉树一元和二元林分材积生长率模型的参数变动系数均在50%以下,变动小,模型稳定可靠。
3) 利用建模样本对桉树一元和二元林分材积生长率模型的残差随胸径和年龄分布的残差图进行分析,均呈随机分布,不存在明显偏差。
4) 桉树一元和二元林分材积生长率模型利用建模样本进行检验,TRB的整体指标值近似等于0,MSB的整体指标值为0,模型拟合方法正确、无系统偏差、预估精度高、适应性能良好。
充分说明桉树的林分材积生长率模型相关紧密、稳定可靠、无系统偏差、预估精度高,可直接用于生产。在实际工作中,可直接应用一元林分材积生长率模型,但如果要得到更高精度的预估值,则应采用二元林分材积生长率模型。需要注意的是,这里的林分材积生长率仅指活立木(或保留木)的材积生长率,它可以反映林分的实际生长速度。如果需要预测林分各生长分量的动态变化,则还需要对林分的进界生长率及未测生长率进行估计。
[1] 骆期邦,曾伟生,贺东北.林业数表模型理论、方法与实践[M].长沙:湖南科学技术出版社,2001.
[2] 廖志云,曾伟生.西藏自治区主要树种生长率模型的研建[J].林业资源管理,2006(3):36-43.
[3] 陈振雄,肖前辉,甘世书,等.海南省桉树、木麻黄、相思树常用数表编制报告[R].长沙:国家林业局中南林业调查规划设计院,2012:1-5
[4] 黄湘南,陈振雄,甘世书,等.第八次全国森林资源清查海南省森林资源清查成果[R].长沙:国家林业局中南林业调查规划设计院,2013:15-20.
[5] 北京林学院.测树学[M].北京:中国林业出版社, 1984.
[6] 陈振雄,贺东北,贺鹏.利用混合模型方法建立海南省橡胶树立木材积方程[J].中南林业科技大学学报,2016,36(12):31-36.
[7] 陈振雄,贺东北,丁长春.利用度量误差模型方法建立海南省桉树、木麻黄、马占相思重量与材积相容性模型[J].中南林业调查规划,2013,32(4):4-11.
[8] 陈振雄,贺东北,肖前辉.海南省桉树、木麻黄、马占相思削度方程研建[J].中南林业调查规划,2012,31(3):11-14.
EstablishmentofGrowthRateModelsforEucalyptusrobustainHainan
ZHOU Xianghong1,JIA Jia2,CHEN Zhenxiong1
(1.Central South Forest Inventory and Planning Institute of State Forestry Administration,Changsha 410014,Hunan,China;2.Forest Survey and Design Institute of Huaihua City,Huaihua 418000,Hunan,China)
Taking data of 3 642Eucalyptusrobustastanding timbers, 135Eucalyptusrobustafield testing spots of 1998, 2003 and 2008 continuous forest inventories in Hainan Province as studying cases, we established diameter growth rate, volume of timber growth rate for single tree and volume of timber growth rate for forest models ofEucalyptusrobusta.These models were with good fitting effect, no systematical errors, the evaluation accuracy of diameter growth rate model were high than 96%,unary and binary volume of timber growth rate for forest were both higher than 99%, which will provide refences for all kinds of forest resource evaluations ofEucalyptusrobustaforest in Hainan Province.
Eucalyptusrobusta;growth rate;continuous forest inventory;equations;Hainan
2017-08-24
海南省林业厅重点项目“海南省桉树、木麻黄、马占相思常用数表研建”(HNHJ2011-01-005)。
周湘红(1969-),女,湖南桃源人,工程师,主要从事森林资源监测和林业规划设计等工作。
S 758.62;S 792.39
A
1003-6075(2017)03-0042-04
10.16166/j.cnki.cn43-1095.2017.03.010

