矩阵的三种等价关系及其分类
黄述亮
(滁州学院 数学与金融学院,安徽 滁州 239000)
线性代数在自然科学和社会科学的等众多领域(如计算机辅助设计、软件工程、数字信号处理等)中有着广泛的应用,其中包含的矩阵思想和方法是处理很多数学问题的重要工具。线性代数的主要研究内容基本上可以归结为矩阵问题,涉及到的主要运算是矩阵的初等变换。将集合按照一定的规则进行分类是集合论中的一种常用方法,而等价关系对于集合的分类起着重要的作用。同时,等价关系是进一步学习相关数学课程(如抽象代数)的基础,不少学者在这方面做了探讨,得到了很多结果[1-5]。特别需要指出,智婕[6]利用非常直观的形式展示了利用等价矩阵求逆矩阵、相似矩阵求Jordan标准形、合同矩阵化二次型标准形时的作用。总之,等价矩阵、相似矩阵及合同矩阵这三个概念非常重要,在学习线性代数的过程中出现的频率很高,并且和许多问题有内在联系。文章将深入挖掘三者之间的关系,这将有助于加深对相关问题的理解和把握。
1 等价关系与集合的分类
在集合论中,假设集合A≠Ø,则称A×A的一个子集R为A的一个二元关系,它可以用来判断集合的元素之间是否具有某种性质。特别的,条件更强且更重要的的二元关系是所谓的等价关系,它要求具备自反性、对称性和传递性三个条件。集合的分类是数学中一个非常重要的概念,如果蕴含 Ai∩ Aj=Ø,那么子集族称为A的一个分类,其中I为指标集。在给定集合的一个分类后,每一个子集Ai(i∈I)都是A的一个类,关键的一个问题就是类中代表元的选择。事实上,类里的任意一个元素都可以充当代表元,而且同一类中的不同代表元有相同的属性,具体问题中往往选择结构最简单的元素作为代表元。
众所周知,集合的分类和集合上的等价关系之间有内在联系,有下面的结果:
定理1.1[7]给定集合A的一个分类规定aRb⇔a,b在同一个类,则R是A上的一个等价关系。
定理1.2[7]设R是A上的一个等价关系,令[a]=,其中 a∈ A,则就给出集合A的一个分类。
2 矩阵间的三种等价关系与分类
考虑某个数域F上全体n阶方阵组成的集合Mn(F),对于A,B∈Mn(F),按照下面方式规定二元关系:

这里P,Q是可逆矩阵。
经过验证发现,上面给出的三个二元关系都是等价关系,因此可以对全体矩阵进行分类。
首先,从矩阵等价的概念中可以直接看出,等价的矩阵必然同秩,反之也成立。于是,在矩阵等价意义下,按照矩阵秩的大小,全体n阶矩阵Mn(F)可以被分成n+1个互不相交的子集的并集:

这样,从每个类中可以选择一个结构最简单的矩阵做为代表元。由此可以看出,矩阵的秩在矩阵的等价关系下是一个常量。
所有患者都满足中医的中风诊断要求以及西医的脑出血、脑梗塞诊断要求[2,3]。入选条件:(1)年龄35~75岁;(2)病程不足半年;(3)初次发病,且伴有单侧偏瘫;(4)主动治疗,自愿参与本研究。排除条件:伴有心肌梗死、严重肝肾功不全、重度感染、凝血功能障碍、意识障碍等患者。
其次,矩阵 A,B∈Mn(F)相似需要很强的限制条件,但是可以通过它们对应的λ矩阵等价来刻画:两个矩阵A和B是否相似的问题就转化成为验证是否有相同的不变因子。用抽象的线性空间(或者说线性变换)的语言来说就是:同一个线性变换在空间中两组不同基下对应的矩阵相似。显而易见,按照矩阵的相似关系可以把全体n阶复矩阵进行分类,总共有无穷多个等价类。这里指出,不变因子组在矩阵相似下是一个不变量。
最后,对于矩阵之间的合同,可以分成实数域和复数域两种情形来考虑。如果在复数域上讨论矩阵的分类,显然两个矩阵合同等价于它们有相同的秩,从而分类和矩阵等价的分类一致。如果在实数域上讨论该问题,可以按照矩阵的秩r和正惯性指数p两个指标来分类:

此时,全体实n阶矩阵分类如下:
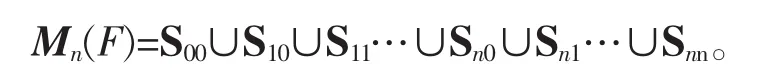
由此可以看出,矩阵在合同下的不变量有两个,我们可以选择秩r、正惯性指数p、负惯性指数q和符号差p-q中的任意两个指标对全体实矩阵进行分类。
3 三者之间的关系
从上面的定义中可以看出,等价矩阵、合同矩阵、相似矩阵都可以保持矩阵的可逆性不变,并且它们之间具有一定的区别和联系。显然,矩阵的合同与相似是矩阵等价的特殊情形:假如两个矩阵合同或者相似,那么一定等价,反之不然;矩阵的等价在上述三个关系中条件最弱;矩阵的相似和合同之间没有必然的联系,但是当定义中出现的可逆矩阵恰好是一个正交矩阵时,矩阵的相似和合同就变成了同一个概念。借助于初等矩阵,上面三种关系可以描述如下:
A 与 B 等价,则有初等矩阵 P1,P2,…,Ps,Q1,Q2,…,Qs使 B=PsPs-1… P1A Q1Q2… Qt,根据初等矩阵和初等变换的对应定理[8],上式表明对矩阵A做若干次初等行变换和列变换,而对于变换的方式没有任何要求。
A与B相似,则有初等矩阵P1,P2,…,Ps使B=PsPs-1…P1AP1-1P2-1…Ps-1,这要求对矩阵做行列变换的次数相同,而且变换方式是同种类型。
由此得到一个结论,上面关于矩阵的三个关系本质上都是矩阵之间的初等变换,只是变换的方式有些不同。此外,三者之间的关系可以用数学中著名的Venn图描绘如下:
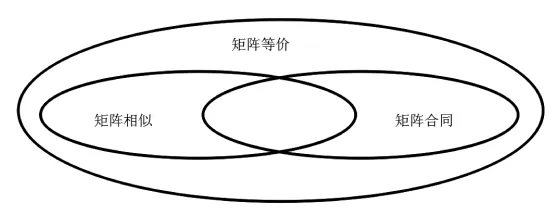
图1 矩阵合同、相似、等价三者之间关系图Figure 1 Relationship between matrix contract,similarity and equivalence
下面是几个概念之间不能互推时的一些反例。
例3.1 设则B=PTAP,因此 A 与 B 合同,显而易见,Tr(A)=1+3≠ 1+2=Tr(B),从而 A 与 B 不相似。
例3.2 设则B=P-1AP,即A与B相似。如果A与B合同,则B=得到矛盾等式
例3.3 设则这说明A与B等价。如果A与B合同,则B=QTAQ,令得到矛盾关系式:ab+cd=0,ab+cd=1。
例3.4 设则,该式说明A与B等价。如果A与B相似,则有可逆矩阵Q,使得B=Q-1AQ=Q-1EQ=E=A,这与题设矛盾。
4 应用举例
下面的例子表明矩阵的等价、相似和合同在证明相关问题时发挥着重要作用。
例4.1 设 A是m×s矩阵,B是 s×n矩阵,证明r(AB)≥ r(A )+r(B)-s。
证明:令 r(A )=p,r(B)=q,则有可逆矩阵 P1,P2,Q1,Q2使得从而令则C是s阶可逆矩阵,于是由于矩阵P1和Q2均可逆,故等价,必然同秩。经过比较可以看出,矩阵C1是从矩阵C中去掉s-p个行和 s-q 个列得到,于是 r(AB)=r(C1)≥ s-(s-p)-(sq)=p+q-s。
例4.2 设A和B为n阶方阵,证明:A与B相似⇔A=PQ,B=QP这里P与Q中至少有一个是可逆矩阵。
证明:(必要性)如果A和B相似,那么存在可逆阵 P,满足 B=P-1AP。记 P-1A=Q,则 A=PQ,B=QP。
(充分性)如果A=PQ,B=QP,其中P为可逆矩阵,那么Q=P-1AP,于是B=P-1AP,即A与B相似。
例4.3 设A和B都是n阶实对称矩阵,证明:如果A和B相似,则A和B合同。
证明:因为A和B相似,根据相似矩阵的性质,它们具有相同的特征值。假设A和B的全体特征值(重根按照重数计算)分别为 λ1,λ2,… λn。由于 A 和 B 都是实对称矩阵,因此有正交矩阵Q1和Q2使,其中
于是这里是可逆矩阵,即A与B合同。
[1]郭增晓.用等价关系对矩阵进行分类[J].石家庄大学学报,2000,12(2):23-24.
[2]谢晓华.矩阵的等价关系与分类 [J].科技视界,2014,(21):196-196.
[3]王晓玲,侯建文.矩阵三种关系间的联系[J].山西农业大学学报,2004,24(2):189-190.
[4]胡婷.论矩阵的三种等价关系[J].科教导刊,2012(32):255-256.
[5]孙晓霞.论等价关系在线性代数学习中的重要性[J].教育教学论坛,2016(5):172-173.
[6]智婕.矩阵等价、相似、合同的联系[J].牡丹江师范学院学报,2011,76(3):76-77.
[7]朱平天,李伯葓,邹园.近世代数[M].北京:科学出版社,2001.
[8]谭玉明,王圣祥,黄述亮.线性代数及其应用[M].上海:上海交通大学出版社,2016.

