液固两相射流冲击磨损的数值计算与实验研究

赵彦琳，曾子华，葛少恒, 3，姚军,



液固两相射流冲击磨损的数值计算与实验研究

赵彦琳1，曾子华2，葛少恒2, 3，姚军1, 2

(1. 中国石油大学 (北京) 机械与储运工程学院，过程流体过滤与分离技术北京市重点实验室，北京，102249;2. 厦门大学 能源学院，福建 厦门，361005；3. 江苏城乡建设职业学院，江苏 常州，213147)

应用实验与数值模拟研究液固两相射流对不锈钢材料的冲蚀磨损行为，分析不同质量分数、粒径情况下样品的平均磨损率，并基于数值模拟预测不同射流速度工况下的冲刷磨损率，最终建立冲刷磨损率与射流速度的关系模型。研究结果表明：单相射流流场的数值模拟结果与实验结果吻合较好；在距离射流中心区域不同径向距离上，平均速度的变化趋势较一致；在近壁面处，射流轴向速度突然减小，造成雷诺切应力增大。在远离壁面处，其法向速度逐渐增大，脉动速度相应增大，雷诺切应力增大；当射流继续远离壁面时，雷诺切应力开始减小直到趋近于0；在喷嘴正下方，压力分布存在1个滞止区，此处压力高于四周压力；下游冲刷磨损率先升高再稍微下降，而上游冲刷磨损率明显下降；实验样品表面微观测试结果验证了不同区域冲刷磨损率分布的正确性。

液固两相；射流；磨损；数值计算

在水利水电工程、航空航天工程、给水排水工程、环境工程以及化工、冶金、能源、机械等许多领域，都会遇到大量的射流冲击问题。由于射流冲击具备高效的传热效率，其被广泛应用于诸多工业场合，例如玻璃面板的回火、金属面板的低温处理、丝质和纸质品的干燥、汽轮机加热和电子设备部件的冷却等。由于射流冲击的传质特性，其也被广泛应用于采矿通风、隧道工程、喷涂工程以及空化钻井等领域，此外，在飞行器垂直起降领域，冲击射流也得到广泛关注[1]。对于多相射流，流场中存在的第2相固体颗粒会对流场的结构和湍流特性产生一定的影响，反之，流场的结构和和湍流特性改变后又会反作用于固体颗粒，颗粒在流场中的扩散特征也会随之发生改变，固体颗粒和流体的这种耦合特性使两相流的研究变得更复杂。CROWE等研究了颗粒在涡中的运动行为，并取Stokes数()作为特征参数，其研究表明：当>>1时，颗粒会加强流体湍流，颗粒运动相对独立，可以穿透涡结构；当<<1时，流体湍流度将会因为颗粒的存在而被抑制，这时颗粒也将随着涡结构的运动而运动，但不会穿透涡结构；当≈1时，颗粒与流体相互作用机理比较复杂，YAO等[3]的研究表明颗粒会在涡结构边界汇聚。ZHANG等使用激光多普勒测速仪研究了冲击射流中流体速度分量场与颗粒速度分量场，并与实验二阶雷诺应力模型的数值模拟结果进行了比较，结果显示CFD模拟预测得到的颗粒碰撞速度与实测的结果吻合较好，从而为进一步计算冲刷磨损打下了基础。樊建人等[5]提出气固两相流动的湍流脉动扩散数学模型，使用−双方程模型求解气相湍流场，根据气相湍流脉动频谱、能谱曲线提出了随机富氏级数模拟气相脉动速度，并用拉格朗日方法描述颗粒运动。此外，为了便于工程实际应用，樊建人等[5]给出了颗粒速度场和浓度场的计算方法。姚军等[6]通过直接数值模拟方法计算了圆柱尾流中颗粒运动，分析总结了不同以及不同雷诺数下颗粒扩散运动的特性，并发现粒径是决定其扩散特征的重要因素；此外，该研究发现颗粒在流场中心轴线附近的扩散机理主要取决于速度梯度和压力梯度产生的吸引力。姚军等[7]进一步研究了颗粒−壁面碰撞后发生静电的机理。

1 实验方法

本文所采用的实验装置示意图如图1所示，整个循环冲蚀装置包括功率为1.5 kW的水泵、循环水路、直径为13 mm喷嘴、水箱以及高速摄像仪。实验中喷嘴与样品的夹角为30°、距离为20 mm，喷嘴的冲击水流速度为10.5 m/s。实验时，液固两相流在管道中不断循环流动，流经喷嘴冲击到实验样品，水流速度通过高速摄像仪测得。第1组实验分别在1/6，1，3，4，5，7，9和11 h时取样品称质量，用500倍显微镜 (Axio Observer A1m金相显微镜)观察并记录样品表面微观组织结构。第2组实验每隔3 h称质量，并在12 h和39 h用扫描电子显微镜(S−4800扫描电镜)观察并记录。第3组实验冲蚀2 h后用扫描电镜拍照。

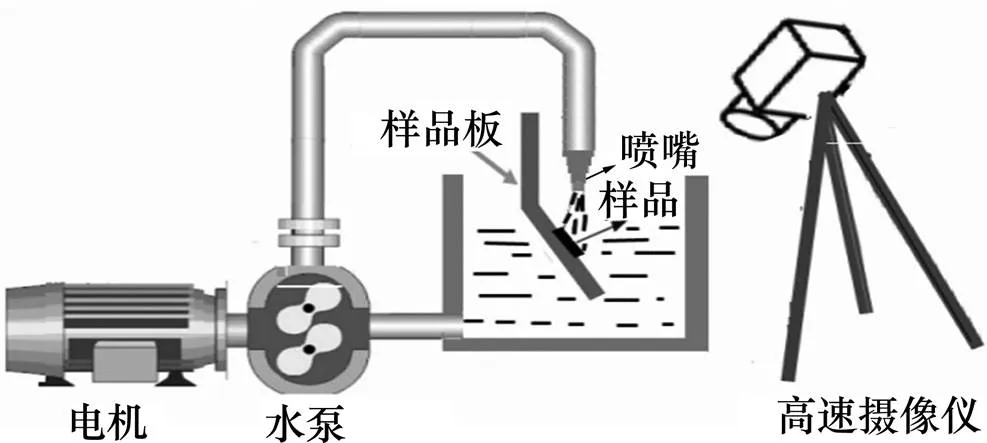
图1 实验装置示意图

在实验中主要关注颗粒粒径、质量分数、材质以及样品材质对流体冲刷磨损的影响。实验进行之前排除其他可能影响实验结果的因素，如水温、取样方式、环境等，有效地降低了实验误差。在实验进行过程中，循环水泵的持续工作会给系统带来一定温升，经测量，在室温条件下长时间运行温升会超过10 ℃，达到一定程度后就不再升高，保持在一定值。在不同温度下进行相同实验，发现温度变化对冲刷磨损量影响很小，所以，可忽略温升带来的影响。本实验采取间断取样方式，通过比较发现，在相同时间内一次性连续冲刷与多次反复间断冲刷所得到的实验结果一致，因此，取样方式对实验结果的影响可忽略。此外，对冲刷磨损过的样品在室温环境下放置48 h后称质量，样品质量没有发生变化，同时样品表面也没有发现颜色变化，所以，环境对冲蚀后样品的影响也可忽略。

2 计算方法

2.1 流场计算

在本文数值计算工作中，采用雷诺应力模型计算流场，即直接对雷诺方程中脉动应力建立微分方程。在直角坐标系中建立不可压缩流体的连续性方程、动量方程：

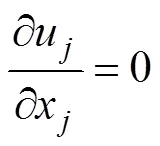
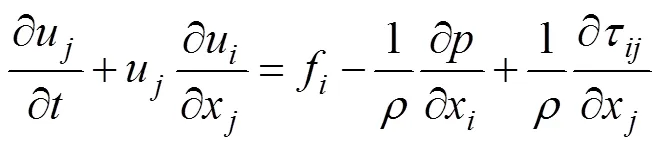
雷诺应力方程模型方程形式如下：

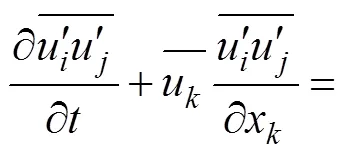
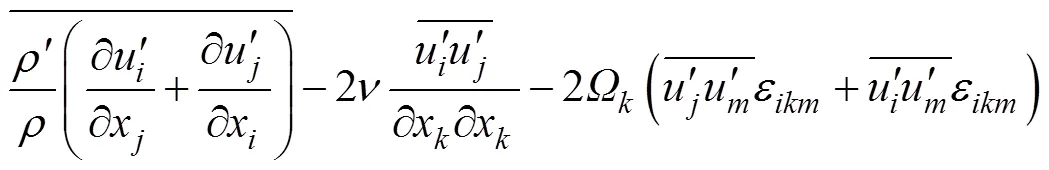
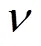
2.2 离散相控制方程

颗粒轨迹采用拉格朗日方法进行求解。流场中颗粒质量分数为0.5%，连续相流体和离散相颗粒的密度相差大，因此，可忽略固体颗粒受到的绕流阻力、附加质量力、流场压力梯度引发的附加力、颗粒旋转升力等作用力以及颗粒间的碰撞。基于此，固体颗粒运动方程可写为[3, 8]：

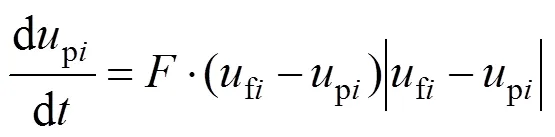
(5)

(6)

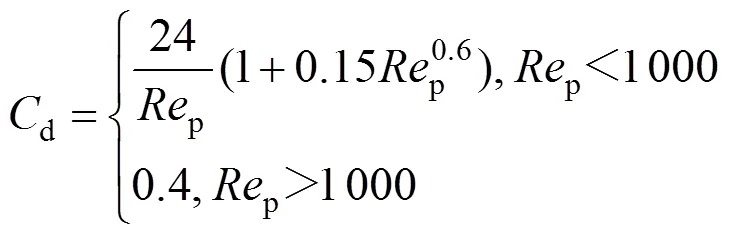
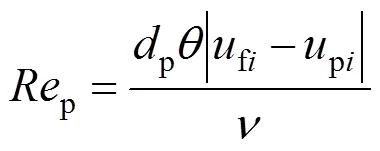
式中：为冲击角度。

2.3 磨损模型

应用ZHANG等[9]提出的腐蚀与冲蚀研究中心的计算模型，完成冲蚀磨损率的计算。综合考虑固体颗粒冲击速度、冲击角度、壁面材料硬度、固体颗粒形状等因素对冲蚀磨损的影响的磨损模型为：

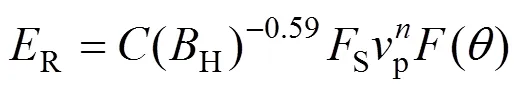
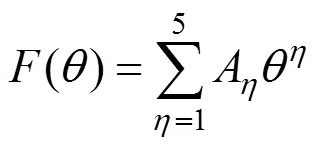
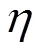
2.4 壁面反弹模型

固体颗粒撞击壁面时存在能量的转移和损失，表现形式为热传导、样品表面磨损等。本文模拟中确定的壁面恢复方程如下：

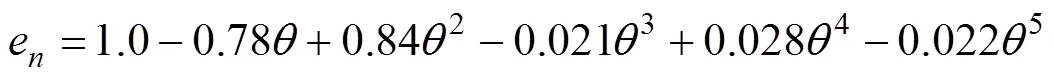
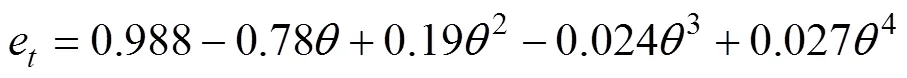
式中：­e和e分别为法向和切向磨损系数。

3 分析与讨论

3.1 单相射流数值模拟

3.1.1 计算条件

在单相冲击射流的流场结构和传热特性的实验研究方面，研究者进行了大量的研究[10−14]，数值模拟研究也取得很大进展[15−18]。由于网格精度要求，使用 LES(大涡模拟)方法模拟较高雷诺数的冲击射流仍具有一定难度，而使用DNS(直接数值模拟)方法又仅限于低雷诺数的情况[5]。圆形冲击射流由于喷嘴物理结构复杂，使用数值模拟较困难，因为在喷嘴出口处，开尔文−亥姆霍兹不稳定性(Kelvin−Helmholtz instability)形成了卷起的漩涡，在下游漩涡破裂并且会影响到外围的壁面射流。本文主要模拟了较小喷嘴壁面间距(/=2，为喷嘴出口与壁面的距离，为管路直径)情况下冲击射流的流场信息，并与COOPER等实验结果进行比较。

根据实验装置建立计算区域，如图2所示。计算区域保证了能够正确地模拟多相流流动特征以及磨损行为，主要包括喷嘴、冲击样品区、水箱底层以及计算区域。边界条件设置为：喷嘴进口为速度入口，喷嘴壁面、冲击壁面以及底部均为无滑移固体壁面，上边界以及4种边界为压力出口边界条件，离散项边界类型为反射(reflect)；网格的划分采用混合多面体网格，并在冲击壁面附近进行了加密处理，数量为185万个；计算所使用的软件为研究团队多年发展的计算软件；所采用的湍流模型为RNG−模型；壁面处理函数使用加强的壁面处理方式；速度压力耦合方式为SIMPLE算法，对流项和扩散项应用一阶迎风格式，模型所控制的残差精度为10−。

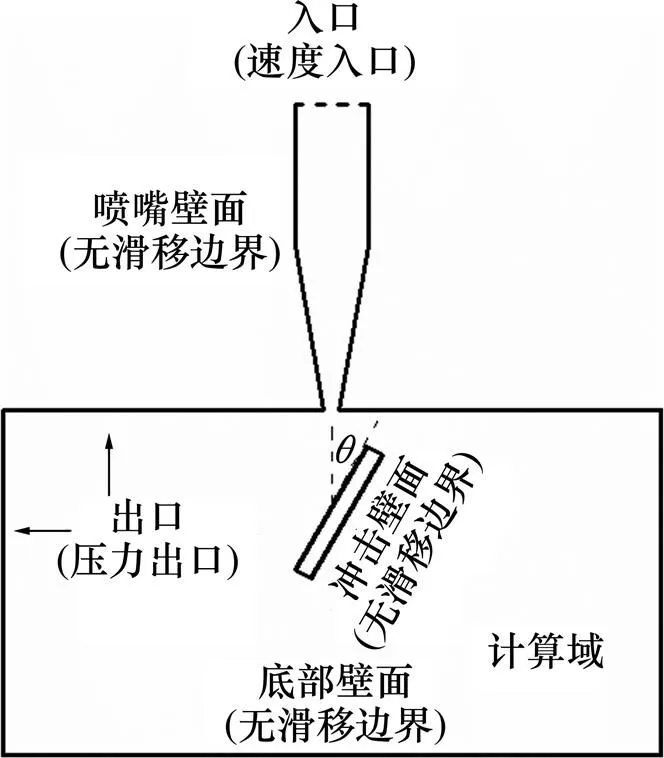
图2 计算区域及边界条件

3.1.2 计算验证

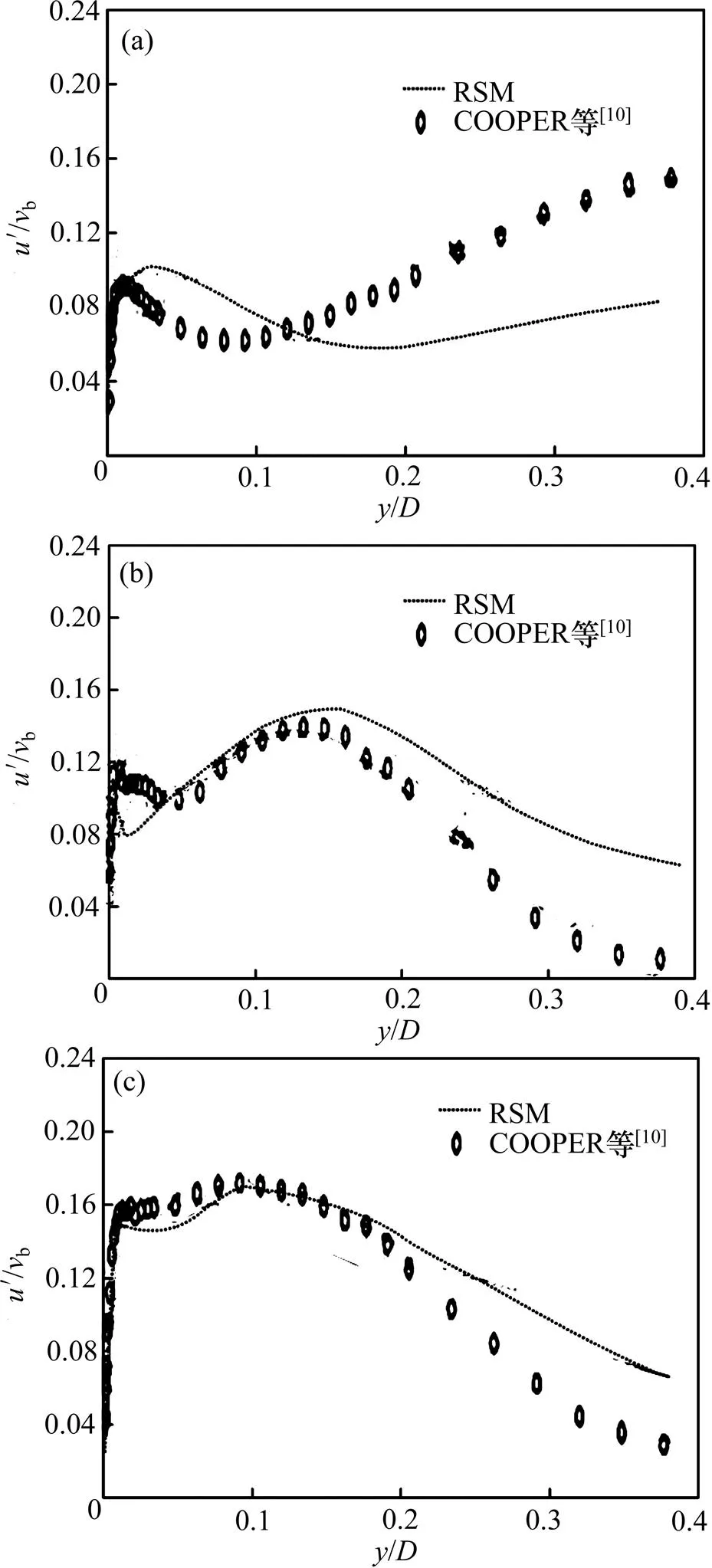
图3所示为冲击射流不同径向距离上径向脉动速度′(利用管道内体积流速b进行量纲一化)与实验测量结果的比较，选取为0.5，1.0和2.5 (为距离管路中心的距离)。由图3可见：计算结果与实验结果在趋势上有较好的一致性，但是在为0.5处有较大偏差，此处靠近轴线，上游形成的漩涡对此位置影响较大。脉动值呈现先减小再增大的趋势；在为1.0和2.5处，计算结果与实验结果较吻合，但与=0.5不同，它们均呈现先减小、增大再减小的趋势。

r/D：(a) 0.5；(b) 1.0；(c) 2.5

横向比较，在靠近壁面的位置，越往外围，即越大，径向脉动速度越大。这是流体从滞止点开始加速引起剪切力作用的结果，继续往外围移动，剪切力减弱导致湍流强度相应减弱，所以，从滞止点向外围径向脉动速度会有先增大再减小的趋势。因此，本数值模拟基本能获得径向脉动速度的趋势，但在轴线附近有一定的误差，在外围表现稍好。

图4所示为冲击射流不同径向距离上轴向脉动速度′与实验测量结果的比较，选取为0.5，1.0和2.5。由图4可知：计算结果与实验结果有较好的一致性，但在=2.5处，计算结果与实验结果存在较大差距。图4(a)所示趋势与图4(b)与图4(c)所示有明显不同，与图3所示结果相近。这是因为在距离轴线附近轴向速度占主导作用，与轴线上的速度较为相似。当逐渐增大时，轴向速度不断衰减，法向速度开始占主导地位，尤其是在距离壁面稍远处，衰减很大，呈现出图4(b)与图4(c)所示趋势。由此可知，本工作所采用的模型能较好地反映该趋势，在数值上也较为接近。

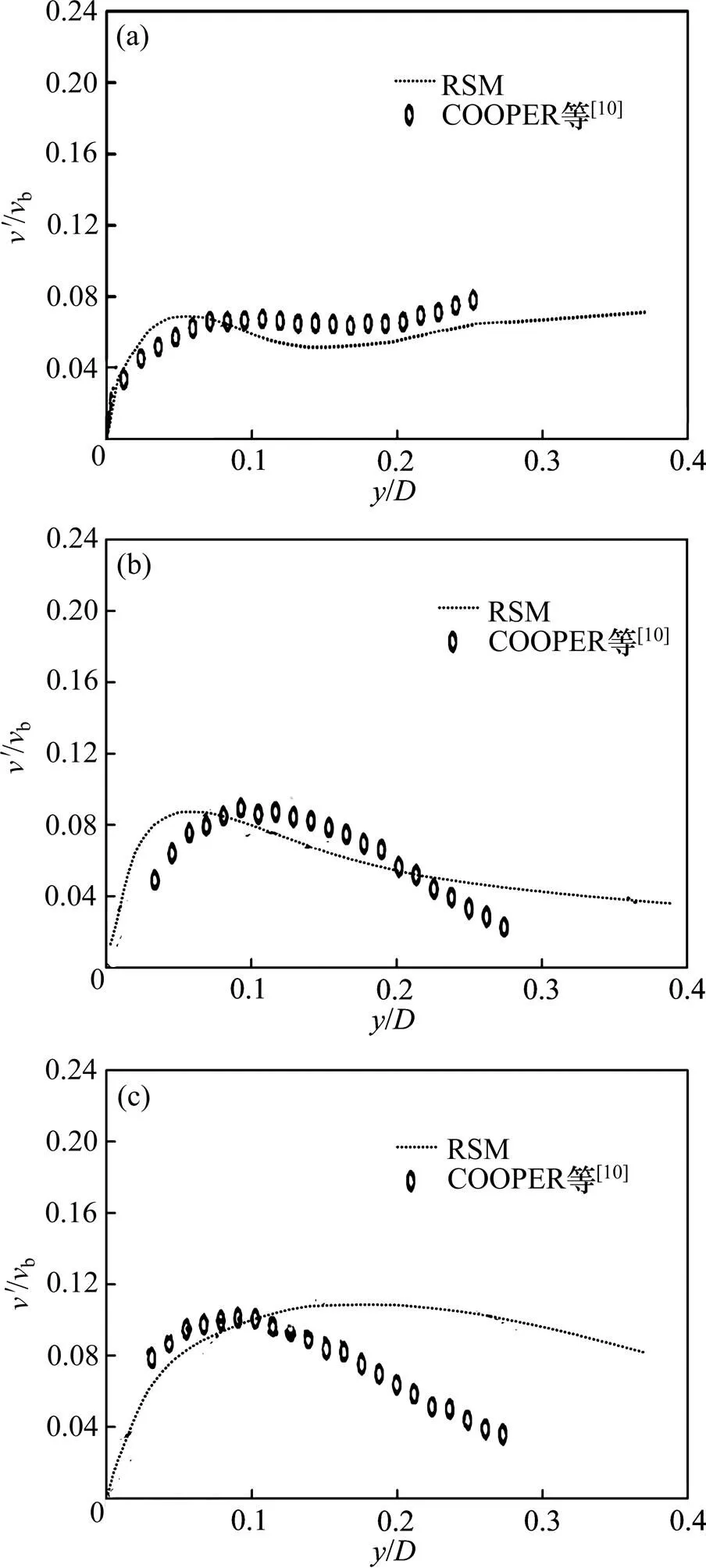
r/D：(a) 0.5；(b) 1.0；(c) 2.5

3.1.3 流场分析

图5(a)所示为液相流体速度云图。由图5(a)可以看到：喷嘴出口处速度为10 m/s左右，流体撞击到冲击面板后向下游流去，图5(b)所示为液相的静压分布云图，在喷嘴正下方压力分布存在一个滞止区，此区压力高于四周的压力，这对颗粒的运行轨迹产生一定的影响，间接造成颗粒与冲击壁面的撞击角度发生改变，对壁面磨损的形成有较大影响，表现为在较大角度斜冲壁面时，壁面会出现越靠近下边缘磨损率越大的情况。

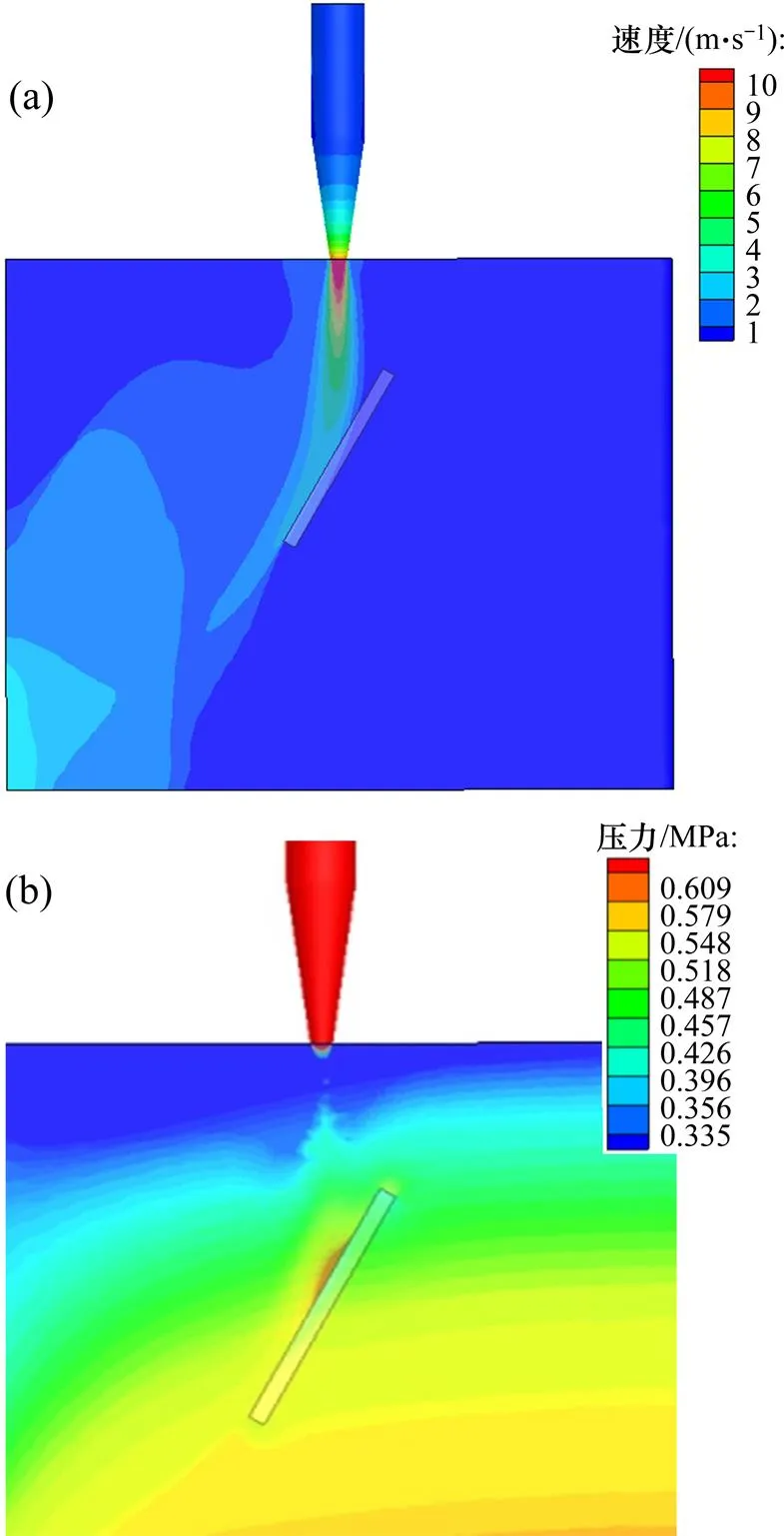
(a) 速度；(b) 压力

将冲击射流的数值模拟结果与实验结果比较可以得出：RSM模型(雷诺应力模型)可以预测与实验结果一致的流动特性，能够准确预测冲击射流壁面附近的流动特性，与实验测量结果较一致；平均速度、脉动速度和雷诺切应力均能反映其变化趋势，大部分在数值上有较高的一致性。但是由于受到流动弯曲、旋转和分离等因素影响，脉动强度的预测值与实验值有一定的偏差。

3.2 两相射流冲蚀的数值模拟

表1 式(10)中Aη取值

计算假设：颗粒的形状均为圆形并且粒径是统一的；忽略颗粒之间碰撞；模拟为单相耦合，即流体作用于颗粒但是颗粒不影响流场的流动。

在本文中，不同条件下模拟计算和实验所得的平均磨损率较接近，模拟结果比实验结果高约10%。具体原因可能有：1) 由于该模型假定颗粒都是圆形并且粒径是统一的，而实验的实际情况是颗粒形状并不很规则，一方面，颗粒在碰撞过程中会破碎，其形状并非规则的圆形，另一方面，颗粒粒径不是统一不变的；2) 为了节约计算时间，本文计算模型忽略了颗粒之间的相互作用以及颗粒对流场的影响，这在一定程度上高估了颗粒的速度；3) 在实验过程中，颗粒会在水箱底部有一定量沉淀，造成两相流中颗粒质量分数与实验结果相比有小幅度下降，而在模拟过程中则假设颗粒均匀分布。本文中数值计算能较好地反映真实磨损情况，同时也验证了磨损模型的正确性，为使用该模型预测在其他条件下的磨损情况奠定了坚实的基础。

图6(a)所示为中心线上磨损率变化趋势，其中，0点位置是样品的圆心位置，正方向为样品的上游位置，负方向为样品的下游位置。由图6(a)可以看出：下游位置的冲刷磨损率远远大于上游的磨损率，随离圆心距离逐渐变大，冲刷磨损率逐渐增大，然后开始部分减小。而上游位置的冲刷磨损率则一直减小，且总体小于下游位置。该现象可以从颗粒流动方向进行解释。由5(a)可以看出流体的流动方向，接触到冲击壁面后向下游流去，同时，由于颗粒粒径较小，有较好跟随性，主要作用于下游位置，造成样品下游的冲刷磨损较严重。

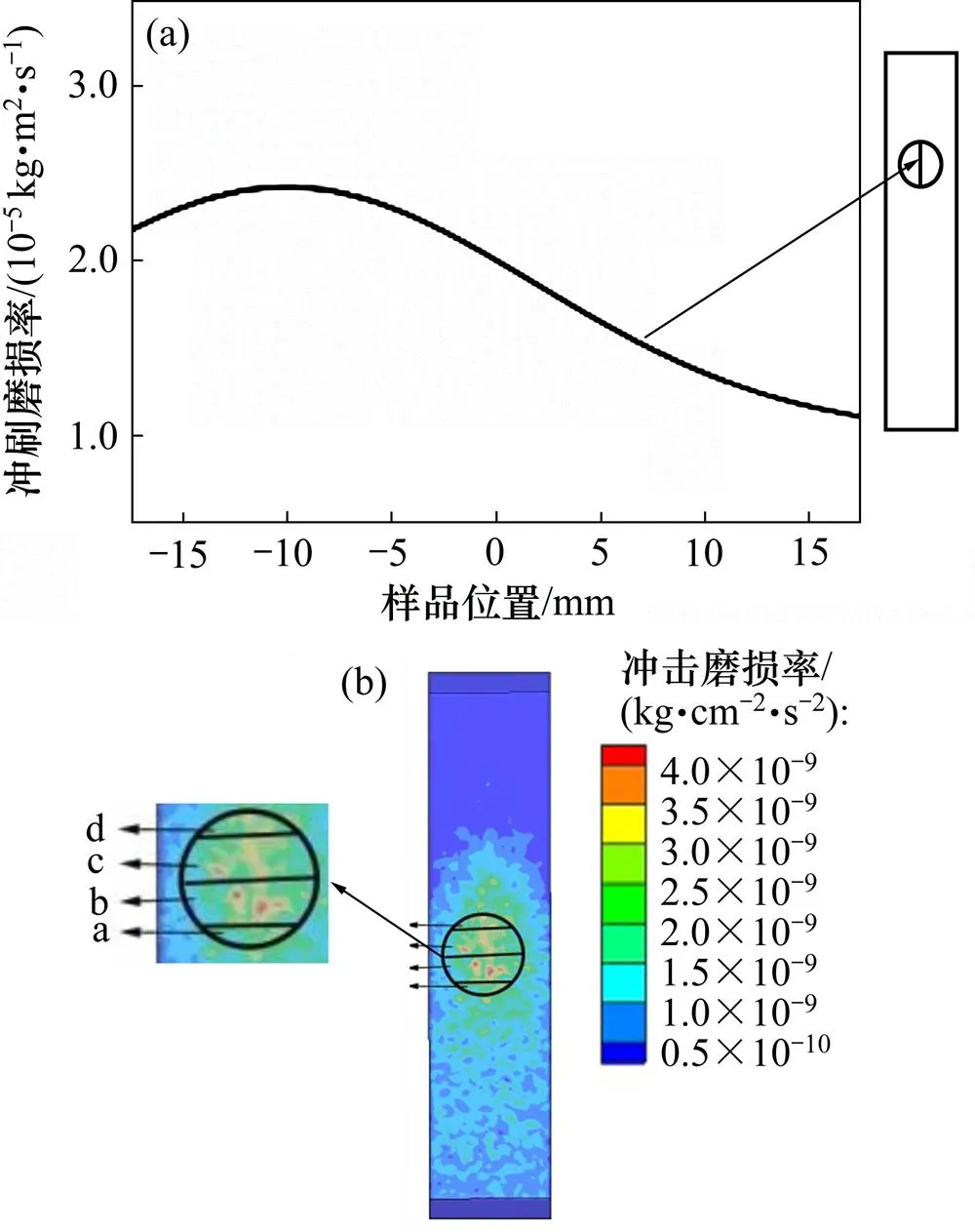
(a) 实验样品中心线上磨损率变化趋势图；(b) 冲击壁面冲刷磨损率云图

图6(b)所示为冲击壁面磨损率云图，圆圈内为样品区，将样品区分为a，b，c和d共4个区域，如图6(b)中放大图所示。从图6(b)可以看出：a区与b区破坏较大，c区与d区破坏相对a区与b区较小，同时a区与b区和c区与d区的破坏形式也不同，这主要是颗粒碰撞的角度不同造成的，a区与b区冲击角度较小，撞击的水平分力较大，破坏形式主要是切削的形式，c区与d区撞击的垂直分力较大，破坏的形式主要是挤压形式，在表面形成压痕。

图7(a)所示为不同粒径情况下中心线上实验模拟的冲刷磨损率，图7(b)所示为不同颗粒质量分数情况下中心线上实验模拟的冲刷磨损率分布。由图7可以看出：不同情况下中心线上的冲刷磨损率分布规律相同，均是往下游方向冲蚀磨损率先增大再减小，往上游则减小，并且计算所得冲刷磨损率随粒径增大而增大，该规律与实验所得规律相吻合。此外，计算的冲刷磨损率随颗粒质量分数增大而增大的规律也与实验结果相吻合。在颗粒质量分数较大的情况下，冲刷磨损率沿中心线方向变化较大，颗粒质量分数较小时变化相对较小。

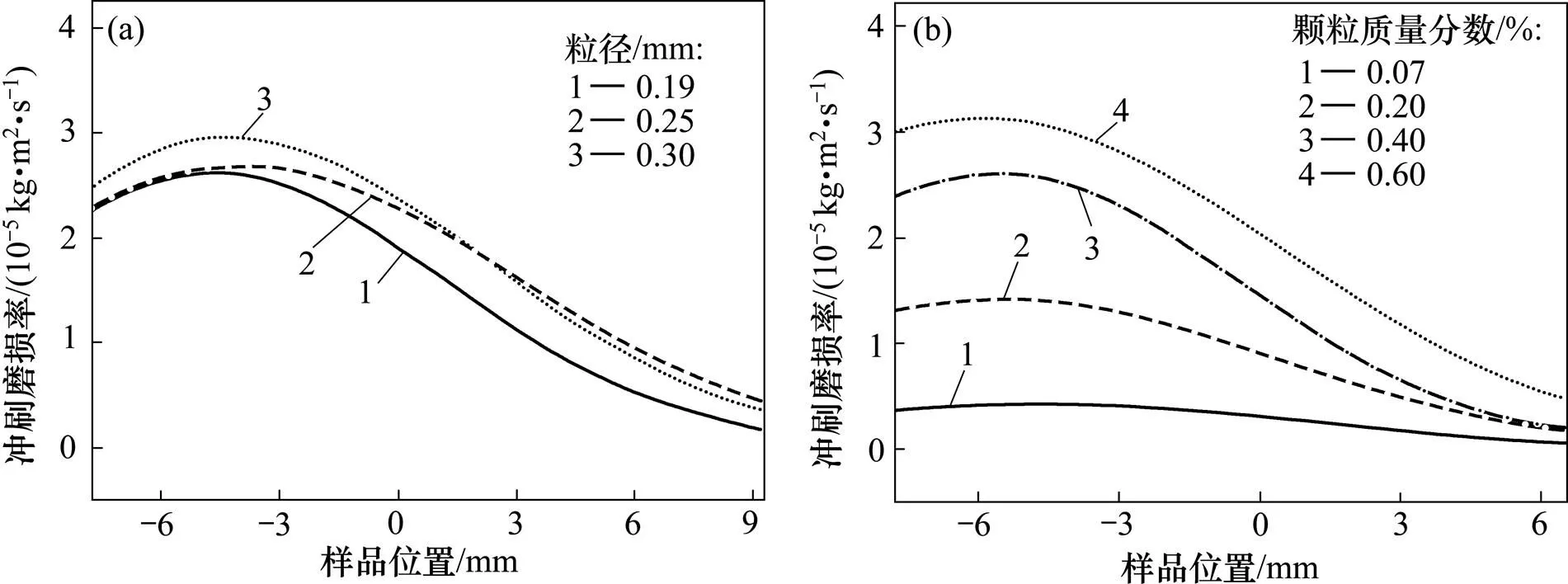
(a) 不同粒径；(b) 不同颗粒质量分数

图8所示为0.2%质量分数、粒径为0.25 mm时，平均冲刷磨损率随速度的变化关系。由图8可见：冲刷磨损率和速度的增加呈指数的关系；冲刷磨损率会随着冲刷的速度快速地增大。文献[18]和[19]中所示结果也呈现出相同的变化趋势。

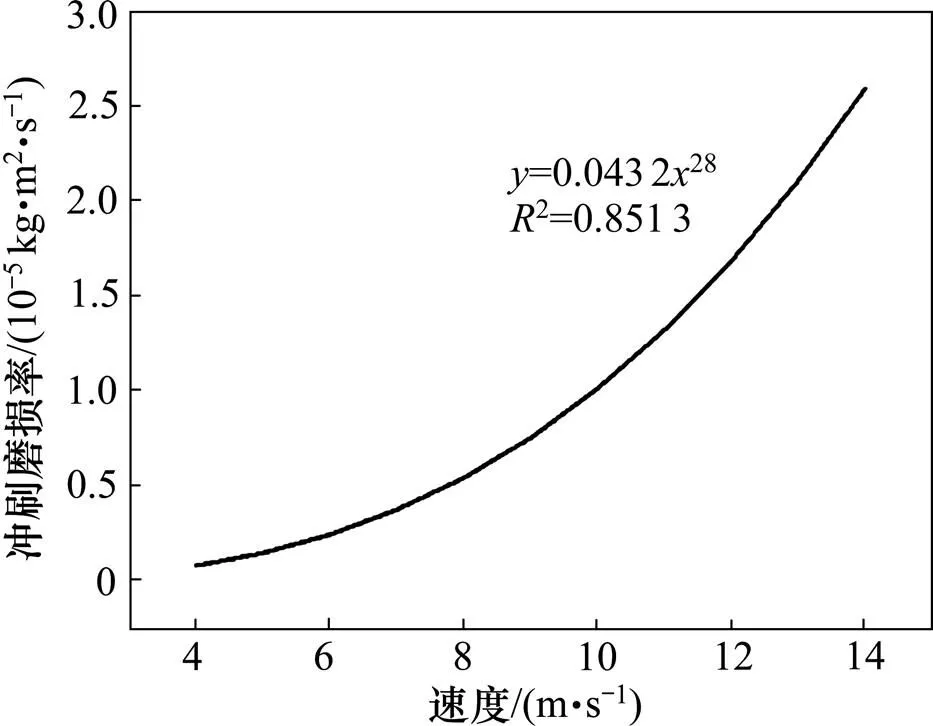
图8 不同速度情况下平均冲刷磨损率和速度的关系

4 结论

1) 在靠近射流中心区域(/=1.0；/=2.5)，不同径向距离上平均速度具有较为一致的变化趋势, 即轴向速度在近壁面(/约为0.03)达到最高之后，远离壁面(/=0)的轴向速度呈现逐渐减小的趋势。这是因为在中心区域轴向速度起到主导作用，随着位置向外围移动，轴向速度的影响逐渐减弱，径向速度起主导作用。

2) 射流靠近壁面时轴向速度突然减小，导致雷诺切应力增大。在/为1.0和2.5处，法向速度起主导作用，远离壁面处法向速度逐渐增大，脉动速度也相应增大，导致雷诺切应力增大；继续远离壁面，雷诺切应力开始减小并渐渐趋近于0。

3) 在喷嘴正下方，压力分布存在一个滞止区，此处压力高于四周压力，对颗粒运动轨迹造成影响，可改变颗粒与冲击壁面撞击角度。另一方面，该滞止区对壁面磨损形成也有较大影响，表现为在较大角度斜冲壁面时，壁面会出现越靠近下边缘磨损越大的现象。

4) 在实验样品表面，下游位置冲刷磨损率远比上游的大，离圆心位置越远，冲刷磨损率越大，后开始减小；上游位置冲刷磨损率不断减小，且总体上比下游位置的小。

5) 冲刷磨损率随颗粒粒径增大而增大，随颗粒质量分数增大而增大。当颗粒质量分数较大时，冲刷磨损率沿中心线方向变化较大；当颗粒质量分数较小时，变化较小。

[1] ZHAO Yanlin, ZHOU Fang, YAO Jun, et al. Erosion-corrosion behavior and corrosion resistance of AISI 316 stainless steel in flow jet impingement [J]. Wear, 2015, 328/329: 464−474.

[2] CROWE C T, TROUTT T R, CHUNG J N. Numerical models for two-phase turbulent flows[J]. Annual Review of Fluid Mechanics, 1996, 28(1): 11−43.

[3] YAO Jun, ZHAO Yanlin, HU Guilin, et al. Numerical simulation of particle dispersion in the wake of a circular cylinder[J]. Aerosol Science and Technology, 2009, 43(2): 174−187.

[4] ZHANG Y, REUTERFORS E P, MCLAURY B S, et al. Comparison of computed and measured particle velocities and erosion in water and air flows[J]. Wear, 2007, 263(1/2/3/4/5/6): 330−338.

[5] 樊建人, 赵华, 岑可法. 气固两相流动的湍流脉动扩散数学模型及其应用[J]. 应用力学学报, 1990, 7(1): 51−56. FAN Jianren, ZHAO Hua, CEN Kefa. Mathematical model of turbulent flow in gas solid two phase flow and its application[J]. Chinese Journal of Applied Mechanics, 1990, 7(1): 51−56.

[6] 姚军, 嵇峰, 刘兰, 等. 圆柱尾迹中颗粒运动的直接数值模拟研究[J]. 自然科学进展, 2003, 13(6): 631−636. YAO Jun, JI Feng, LIU Lan, et al. Direct numerical simulation on the particle flow in the wake of circular cylinder[J]. Progress in Natural Science, 2003, 13(6): 631−636.

[7] 姚军, 黄勇, 吴洁洁, 等. 颗粒速度和形体因素影响静电发生机理[J]. 中南大学学报(自然科学版), 2016, 47(5): 1799−1804. YAO Jun, HUANG Yong, WU Jiejie, et al. Investigation of granule sliding velocity and granule shape effect on electrostatics[J]. Journal of Central South University (Science and Technology), 2016, 47(5): 1799−1804.

[8] SOMMERFELD M. Analysis of collision effects for turbulent gas-particle flow in a horizontal channel(part Ⅰ): particle transport[J]. International Journal of Multiphase Flow, 2003, 29(4): 675−699.

[9] ZHANG Y L, MCLAURY B S, SHIRAZI S A. Improvements of particle near-wall velocity and erosion predictions using a commercial CFD code[J]. Journal of Fluids Engineering, 2009, 131(3): 031303-1−9.

[10] COOPER D, JACKSON D C, LAUNDER B E, et al. Impinging jet studies for turbulence model assessment: i. flow-field experiments[J]. International Journal of Heat & Mass Transfer, 1993, 36(10): 2675−2684.

[11] BAUGHN J W, SHIMIZU S. Heat transfer measurements from a surface with uniform heat flux and an impinging jet[J]. Journal of Heat Transfer, 1989, 111(4): 1096−1098.

[12] COLUCCI D W, VISKANTA R. Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet[J]. Experimental Thermal & Fluid Science, 1996, 13(1): 71−80.

[13] GEERS L F G, TUMMERS M J, HANJALIC K. Experimental investigation of impinging jet arrays[J]. Experiments in Fluids, 2004, 36(6): 946−958.

[14] O’DONOVAN T S, MURRAY D B. Fluctuating fluid flow and heat transfer of an obliquely impinging air jet[J]. International Journal of Heat Mass Transfer, 2008, 51(25/26): 6169−6179.

[15] MATHEY F, COKLJAT D, BERTOGLIO J P, et al. Assessment of the vortex method for large eddy simulation inlet conditions[J]. Progress in Computational Fluid Dynamics: an International Journal, 2006, 6(1/2/3): 58−67.

[16] OLSSON M, FUCHS L. Large eddy simulations of a forced semiconfined circular impinging jet[J]. Physics of Fluids, 1998, 10(2): 476−486.

[17] HADIABDI M. HANJALI, K. Vertical structures and heat transfer in a round impinging jet[J]. Journal of Fluid Mechanics, 2008, 596(1): 221−260.

[18] LODATO G, VERVISCH L, DOMINGO P. A compressible wall-adapting similarity mixed model for large-eddy simulation of the impinging round jet[J]. Physics of Fluids, 2009, 21(3): 338−276.

[19] HONG M, HU X, NEVILLE A. A systematic erosion-corrosion study of two stainless steels in marine conditions via experimental design[J]. Wear, 2007, 263(1/2/3/4/5/6): 355−362.

(编辑 刘锦伟)

Numerical and experimental investigation of erosion by liquid-solid impinging jet

ZHAO Yanlin1, ZENG Zihua2, GE Shaoheng2, 3, YAO Jun1, 2

(1. Beijing Key Laboratory of Process Fluid Filtration and Separation, College of Mechanical and Transportation Engineering, China University of Petroleum, Beijing 102249, China;2. College of Energy, Xiamen University, Xiamen 361005, China;3. Jiangsu Urban and Rural Construction College, Changzhou 213147, China)

Both experimental and numerical method were applied to investigate the erosion wear behaviour of liquid-solid two-phase jet on stainless steel, the average wear rates of samples under conditions of different mass fractions and particle sizes were analyzed, and the wear rates at different jet velocities were predicted based on the numerical simulation, and finally the relationship model of erosion wear rate with jet velocity was established. The results show that the numerical simulations of single-phase flow field agree well with those of the experiments. The mean velocities of impinging jet have similar trends at various radial distances from the core region. The axial velocity near the wall decreases sharply, which causes the increase of Reynolds shear stress. However, apart from the wall, the normal velocity increases gradually as well as the fluctuation velocity, which causes the increase of Reynolds stress. Apart from the wall sequentially, Reynolds stress decreases gradually to zero. A stagnation region is found right below the impinging jet, where pressure is higher than that in other areas. The downstream scour wear rate first increases and then decreases slightly, while the erosion rate for upstream decreases significantly. The microcosmic test on the surface of the experimental sample verifies the correctness of the erosion rate distribution in different regions.

liquid-solid; impinging jet; erosion; numerical simulation

10.11817/j.issn.1672-7207.2018.05.033

TK121

A

1672−7207(2018)05−1289−08

2017−05−11；

2017−07−10

国家自然科学基金资助项目(51776225，51376153，51406235)；中国石油大学(北京)科学基金资助项目(C201602) (Projects(51776225, 51376153, 51406235) supported by the National Natural Science Foundation of China; Project(C201602) supported by the Science Foundation of the China University of Petroleum, Beijing)

姚军，教授，博士生导师，从事多相流基础及应用研究；E-mail: yaojun@cup.edu.cn