含有浮动组合内齿圈的人字齿行星齿轮系统静态均载特性

张霖霖，朱如鹏



含有浮动组合内齿圈的人字齿行星齿轮系统静态均载特性

张霖霖，朱如鹏

(南京航空航天大学 机电学院，江苏 南京，210016)

基于集中参数法，建立含有浮动组合内齿圈的人字齿行星齿轮传动系统静态均载计算模型，并针对其进行静态均载特性行为的理论研究。考虑时变啮合刚度、各构件偏心误差激励、中心构件浮动等影响因素，并利用傅立叶级数法求解系统载荷平衡方程，定性地分析各构件偏心误差、中心构件浮动方式及浮动量、柔性内齿圈扭转刚度等参数对系统静态均载特性行为的影响。研究结果表明：系统均载系数随着偏心误差的增大而增大，构件偏心误差共同作用对均载系数的影响比构件偏心误差单独作用时的影响大；柔性内齿圈扭转刚度的改变对太阳轮、内齿圈的浮动量及系统的均载系数均有影响；含有浮动组合内齿圈的人字齿行星齿轮系统较一般人字齿行星齿轮系统有更好的均载效果。

人字齿；行星齿轮；偏心误差；扭转刚度；浮动；静态均载

人字齿行星齿轮传动系统具有体积小、质量小、传动比大、承载能力强、结构紧凑、传动效率高等优点，在航空、船舶等传动领域有广泛的应用。行星轮间载荷分配均匀性直接关系到传动系统的使用寿命、运转平稳性和工作可靠性，因此，进行人字齿行星齿轮传动系统均载特性的研究具有重要意义。BODAS等[1]利用建立行星轮系的有限元模型来研究各种误差对均载特性行为的影响。LIGATA等[2−4]提出了1个简化模型来预测行星轮的均载特性。BOGUSKI等[5]提出了1个新的方法来测量行星齿轮系中行星轮的均载和太阳轮的径向运动轨迹。FOX等[6−8]分析并验证了弹性销的设计，定量分析了其优点，并用试验研究来证明“弹性销”设计极大地改善了均载性能，行星轮个数越多，效果越好。袁茹等[9]分析了不同支承刚度下，功率在各行星轮间分配不均衡程度和啮合动载荷波动程度。陆俊华等[10]建立了2K−H型行星传动系统的计算模型，从静力学角度分析了系统的均载机理。叶福明等[11]建立了非等模数非等压力角NGW型行星齿轮系的静态均载特性的计算模型，得到一些理论成果。朱增宝等[12−13]分析了误差对人字齿轮系统均载特性的影响。徐向阳[14]研究了柔性销轴刚度和切向误差对行星传动均载的影响，并通过试验验证了理论结果的有效性。盛冬平等[15]建立了双排行星齿轮系统静态均载计算模型，并定性分析了偏心误差、构件支撑刚度及扭转刚度对系统均载的影响。张霖霖等[16]分析了啮合相位对人字齿行星齿轮系统均载的影响，并进行了试验验证。有浮动组合内齿圈的人字齿行星齿轮传动系统的太阳轮在外力作用下可以浮动，在浮动的齿式联轴器作用下具有补偿输入轴相对位移的能力；组合齿圈由柔性内齿圈和浮动内齿圈组成，内齿圈浮动可以减小轮系各构件的作用力的波动量，同时柔性内齿圈为柔性件，轮缘产生径向变形可达到较好的均载效果。尽管国内外众多学者进行了大量关于行星轮系均载特性的研究，然而，到目前为止，尚没有涉及含有浮动组合内齿圈的人字齿行星齿轮的建模和均载特性研究。为此，本文作者建立含有浮动组合内齿圈的人字齿行星齿轮系统的静态均载模型，系统分析构件偏心误差单独作用及共同作用下系统静态均载特性的影响，分析中心构件浮动、柔性内齿圈扭转刚度等对系统均载的影响同时，分析柔性内齿圈扭转刚度对中心构件浮动量的影响。

1 含有浮动组合内齿圈的人字齿行星齿轮系统建模

1.1 含有浮动组合内齿圈的人字齿行星齿轮系统的基本结构

人字齿行星齿轮传动系统结构图如图1所示。整个系统主要由与电机连接的输入轴D、太阳轮s、个行星轮p、行星架c、浮动组合内齿圈以及与负载相连接的输出轴L组成。浮动组合内齿圈由浮动内齿圈r和柔性内齿圈j组成。

太阳轮s可径向浮动，行星轮p由安装在行星架上的滑动轴承来支承，其对行星轮p在向和向的支承刚度分别为Kpx和Kpy。在一些行星齿轮减速器结构中，常常使2个基本构件同时浮动，使系统有更好的均载效果。在含有浮动组合内齿圈的人字行星齿轮系统中，浮动内齿圈r与柔性内齿圈j之间通过直齿相联，柔性内齿圈为薄壁圆筒结构，具有一定的柔性，同时能给内齿圈提供一定支承刚度。输入扭矩D作用在太阳轮s上，外部负载L作用在行星架c的输出轴上。系统静力学模型中不考虑部件自重，不考虑行星轮的离心力，考虑内齿圈浮动及柔性内齿圈的弯曲刚度、扭转刚度。

(a)结构简图；(b) 三维模型图

1.2 含有浮动组合内齿圈的人字齿行星齿轮传动系统静均载物理模型

1对人字齿轮副可看成由2个斜齿轮副组成。以往研究中通常认为2个斜齿轮副的轴向力相互抵消，因此，忽略轴向振动。但由于误差等因素的存在，左、右2个斜齿轮副的动力学特性不可能完全相同。为了更真实地反映人字齿轮的动力学特性，将连接两端斜齿轮的退刀槽等效为弹簧。由于两端的斜齿轮之间存在横向、纵向、轴向及扭转方向的相对运动，因此，该弹簧具有弯曲刚度、拉伸刚度及扭转刚度。

含有浮动组合内齿圈的人字齿行星齿轮传动系统静态模型如图2所示，图2中：为构件的刚度。每个单斜齿轮分别有沿，和轴的3个平移和绕轴旋转的自由度。柔性内齿圈在浮动内齿圈连接时通常用卡圈固定内齿圈，限制内齿圈轴向窜动，因此，虽然柔性内齿圈是直齿结构，仍应考虑沿，和轴的3个平移和绕轴旋转的自由度；考虑到齿轮左右旋，下标为L时表示人字齿中左旋的斜齿，为R时表示人字齿右旋的斜齿；代表第个行星轮，= 1, 2,…,，为行星轮的个数。该人字行星齿轮传动系统共含有8+24个自由度，则广义坐标为

图2 含有浮动组合内齿圈的人字齿行星传动系统静态模型

式中：，和分别为构件向、向和向的位移；为构件的角位移。

式中：bs，bp，br和j分别为太阳轮、行星轮、内齿圈和柔性内齿圈的基圆半径；c为行星轮中心到行星架回转中心的距离。

1.3 啮合线上的等效偏心误差

将各齿轮各个误差投影到啮合线上的值即为各齿轮的等效偏心误差，并假设沿着啮合线的伸长方向为等效偏心误差的正方向。为了便于研究，本文不考虑变位系数的影响，忽略轴承的支承间隙和齿轮啮合副的齿侧间隙，同时认为行星架的安装和制造误差均包含在行星轮的偏心误差中[11]。齿轮偏心误差以齿轮的实际质心偏离理论坐标原点的距离和角度表示。根据误差定义和啮合线的位置可得太阳轮偏心误差与啮合线的位置关系图，如图3所示。图3中：s为太阳轮圆心；O为第个行星轮的圆心；sp啮合线方向为第个行星轮与太阳轮的啮合线方向。

图3 太阳轮偏心误差与啮合线的位置关系

式中：为时间；s为太阳轮制造偏心误差的初相位；sc为太阳轮与行星架之间的相对转动角速度，且sc=s−c，s为太阳轮角速度，c为行星架角速度。

太阳轮和第个行星轮啮合线与太阳轮偏心误差s的夹角δs为

式中：φ为第个行星轮相对于第1个行星轮的位置角，且φ=2π(−1)/；spt为太阳轮和行星轮啮合副端面啮合角。

式中：b为基圆螺旋角。

图4所示为行星轮偏心误差与啮合线的位置关系。由图4可知：行星轮偏心误差pn在太阳轮和第个行星轮啮合线上的等效误差为e1，行星轮偏心误差pn在第个行星轮和内齿圈啮合线上的等效误差为e2：

图4 行星轮偏心误差与啮合线的位置关系

第个行星轮和太阳轮的偏心啮合误差sn、内齿圈和第个行星轮的偏心啮合误差er分别为

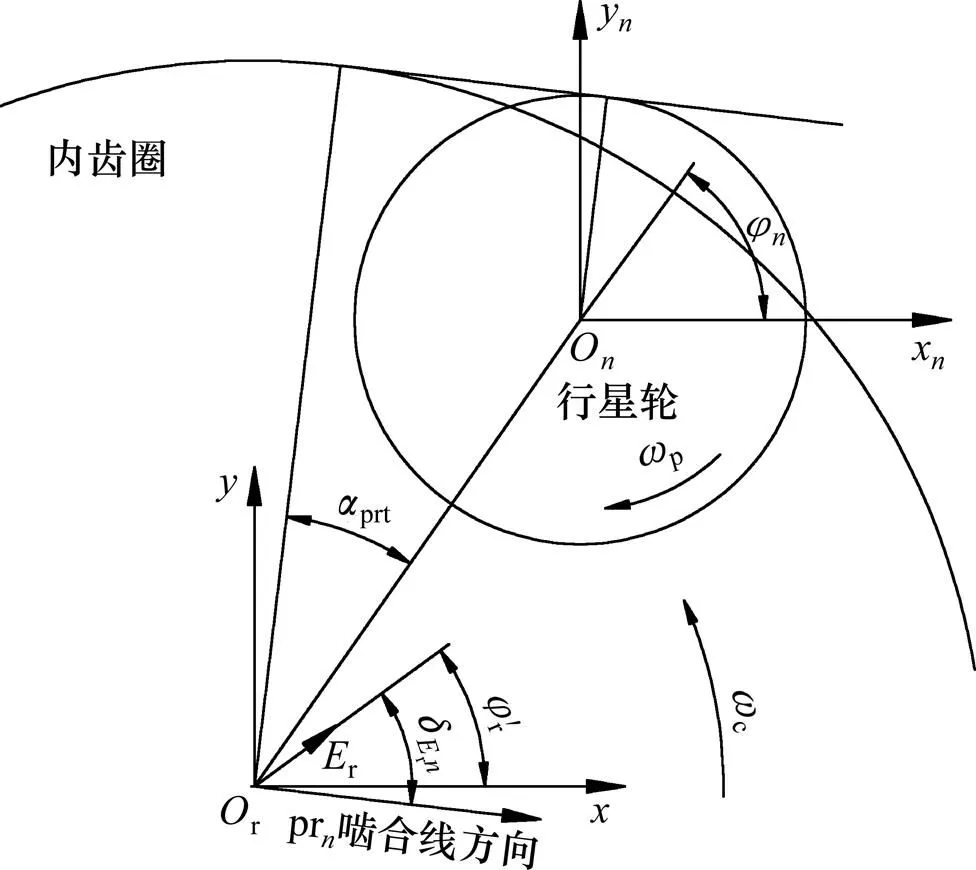
图5 内齿圈偏心误差与啮合线的位置关系

1.4 弹性啮合力

行星轮系中内外各啮合副间的弹性啮合力，可由下式求得：

式中：Fsn和Frn分别为太阳轮与行星轮及行星轮与内齿圈之间的弹性啮合力；Ksn()为太阳轮与行星轮外啮合线上的时变啮合刚度；Krn()为行星轮与齿圈内啮合线上的时变啮合刚度，按MAATAR的斜齿轮啮合刚度公式计算；δsn和δrn分别为内、外啮合线上的相对 位移。

图6所示为行星齿轮中各构件间的相对位置关系在齿轮端面的投影。由图6可以求出各构件之间的相对位移在啮合线或坐标系上的投影。

图6 行星齿轮中各构件间的相对位置关系

太阳轮与行星轮的相对位移沿啮合线方向的投影为

行星轮与内齿圈的相对位移沿啮合线方向的投影为

行星轮与系杆的相对位移沿c，c，c和c方向的投影为

式中：φ为行星轮的圆周角；spt为sp啮合的端面啮合角；rpt为pr啮合的端面啮合角；sn为第个sp啮合的法面啮合线上的综合啮合误差；er为第个pr啮合的法面啮合线上的综合啮合误差。

1.5 系统载荷平衡方程

不考虑动态效应的情况下，根据上述分析可以推导出系统的静态载荷扭矩平衡方程。

太阳轮静态载荷扭矩平衡方程为

可整理为

同理，对于行星轮，有

对于浮动内齿圈，有

对于行星架，有

对于柔性内齿圈，有

式中：下标为L时表示人字齿中左旋的斜齿，取值为1，为R时表示人字齿右旋的斜齿，取值为2；L为输出扭矩；下标g表示构件(如太阳轮s、行星轮p、内齿圈r、行星架c)；表示沿，和轴的3个平移或绕轴的角位移自由度；gρLR为构件g左右旋齿轮间沿向的相互作用力；gρLR为构件g左右旋齿轮间沿向的刚度；Fgρ为构件g在向的支撑力；kgρ为构件g在向的支撑刚度；Frj为内齿圈与齿圈在向的作用力；krjρ为内齿圈与柔性内齿圈在向的支撑刚度；g为构件g的基圆半径。

2 影响静态均载特性的参数

为了从实际应用的角度来分析偏心误差、柔性内齿圈扭转刚度、中心构件浮动等系统参数对人字齿行星轮系的静态均载特性的影响，本文从某齿轮传动系统中提取出相关参数，如表1所示。本文不考虑输入及负载的波动。

采用傅里叶级数法求解式(14)~(18)，获得系统位移响应，代入式(9)得齿轮啮合力。

在人字齿行星传动系统中，各个行星轮承担的载荷并不相等，通常用均载系数来表示传动系统载荷分配均匀性。均载系数越大，传动系统载荷分配就越不均衡。

表1 人字齿行星齿轮系统参数

人字齿行星齿轮系中令左旋各行星轮内、外啮合均载系数为Lspn和Lrpn；右旋各行星轮内、外啮合均载系数为Rspn和Rrpn，则

其中：=1，2，…，。

人字齿行星齿轮系统左旋内外啮合均载系数为Lsp和Lrp；右旋内外啮合均载系数为Rsp和Rrp，则

因此，人字齿行星齿轮系统的静态均载系数[15−16]为

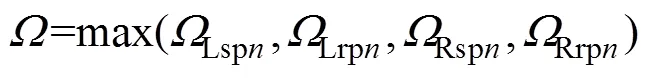
2.1 柔性内齿圈对系统均载特性的影响

为分析柔性内齿圈扭转刚度对中心轮浮动量的影响，定义太阳轮浮动时太阳轮中心的径向浮动量为s；定义内齿圈浮动时内齿圈中心径向浮动量为r[17−18]，则

式中：s和s分别为太阳轮在和方向的位移；r和r分别为内齿圈在和方向的位移。

人字齿轮传动系统中心构件浮动量随柔性内齿圈扭转刚度的变化如图7所示。由图7可知：在改变柔性内齿圈扭转刚度的情况下，内齿圈浮动量随着柔性内齿圈扭转刚度的增大而减小；当柔性内齿圈扭转刚度从5×107N/m增大到2×108N/m时，内齿圈径向浮动量从145 μm急剧减小到90 μm；当柔性内齿圈扭转刚度从2×108N/m增大到1×109N/m时，内齿圈径向浮动量从90 μm缓慢减小到80 μm；而太阳轮浮动量随着柔性内齿圈扭转刚度的增大而增大，当柔性内齿圈扭转刚度从5×107N/m增大到2×108N/m时，太阳轮径向浮动量从70 μm增加到90 μm；当柔性内齿圈扭转刚度从2×108N/m增大到1×109N/m时，太阳轮径向浮动量从90 μm缓慢增加到102 μm。

1—Rr; 2—Rs。

图8所示为人字齿轮传动系统均载系数随柔性内齿圈扭转刚度变化曲线。图8中：Lsp和Lrp分别为系统左旋内、外啮合均载系数；Rsp和Rrp分别为柔性内齿圈扭转刚度对右旋内、外啮合均载系数。由图8可知：在改变柔性内齿圈扭转刚度的情况下，左、右旋内、外均载系数均随着柔性内齿圈扭转刚度的增大而增大。在理想情况下，人字齿轮左、右旋分担相同的扭矩，在同转速下，载荷越大，均载系数越小。系统中左旋外啮合均载系数Lsp小于右旋的外啮合均载系数Rsp；左旋内啮合均载系数Lrp小于右旋的内啮合均载系数Rrp，因此，左、右旋的行星轮系实际分担的系统载荷不同，靠近输入端的左旋会比靠近输出端的右旋分担的扭矩稍多；柔性内齿圈扭转刚度越小，Lsp，Lrp，Rsp和Rrp也越小，同时，4个参数越接近，说明左、右旋分担的载荷越接近，系统的均载效果越好，对系统的使用寿命、运转平稳性更有利。

1—ΩLsp；2—ΩLrp；3—ΩRsp；4—ΩRrp。

2.2 中心构件浮动对系统均载特性的影响

1—太阳轮浮动；2—太阳轮和内齿圈同时浮动；3—太阳轮和内齿圈同时浮动。

2.3 偏心误差对系统均载特性的影响

分析偏心误差作用对均载的影响，先假设构件的其他误差都为0 μm。为研究1齿轮偏心误差单独作用时对系统均载的影响，暂不考虑其他齿轮的偏心误差，带入系统载荷平衡方程，可以分析出太阳轮、行星轮、内齿圈单独作用以及三者共同作用的偏心误差在 0~80 µm内变化时行星轮系均载系数的影响，如图10所示。图10中：s，r和p分别为太阳轮、行星轮和内齿圈偏心误差单独作用的均载系数；为太阳轮、行星轮、内齿圈共同作用下偏心误差的系统均载系数。

随偏心误差增大，系统内部激励就会增大，从而系统的啮合力幅值也会增大，因此，无论偏心误差单独变化还是共同变化，随着偏心误差增大，系统的均载系数都增大。由于行星轮的偏心误差同时影响内、外啮合误差，随着偏心误差增大，行星轮的偏心误差单独变化时系统均载系数增大最快，且当偏心误差一定时，行星轮偏心误差单独作用时的系统均载系数最大，而太阳轮和内齿圈的偏心误差单独作用时的系统均载系数相当。偏心误差共同作用时，太阳轮、行星轮、内齿圈3种偏心误差的相位差和周期不同，因此，各偏心误差共同作用时系统的均载系数大于各偏心误差单独作用时的均载系数。

对比图10(a)和图10(b)可知：在相同工况下及偏心误差作用下，含有浮动组合内齿圈的人字齿行星齿轮系统较一般的人字齿轮系统有更好的均载效果。

(a) 柔性内齿圈扭转刚度为1.5×108 N/m；(b)柔性内齿圈扭转刚度为6.0×107 N/m

3 结论

1) 柔性内齿圈的柔性设计能够改善系统的均载性能，且能够使系统左、右旋行星齿轮分担的载荷更接近，同时，系统的均载效果更好。含有浮动组合内齿圈的人字齿行星齿轮系统较一般的人字齿轮系统有更好的均载效果。

2) 内齿圈浮动量随着柔性内齿圈扭转刚度的增大而减小，太阳轮浮动量随着柔性内齿圈扭转刚度的增大而增大。

3) 太阳轮和内齿圈组合浮动的均载效果比太阳轮单独浮动的均载效果好。当构件浮动与柔性内齿圈耦合时，系统的均载效果最好。

[1] BODAS A, KAHRAMAN A. Influence of carrier and gear manufacturing errors on the static planet load sharing behavior of planetary gear sets[J]. JSME International Journal, 2004, 47(3): 908−915.

[2] LIGATA H, KAHRAMAN A, SING A. An experimental study of the influence of manufacturing errors on planetary gear stresses and planet load sharing[J]. Journal of Mechanical Design, 2008, 130(4): 137−139.

[3] LIGATA H, KAHRAMAN A, SINGH A.A closed-form planet load sharing formulation for planetary gear sets using a translational analogy[J]. Journal of Mechanical Design, 2009, 131(2): 17−21.

[4] SINGH A. Load sharing behavior in epicyclic gears: physical explanation and generalized formulation[J]. Mechanism and Machine Theory, 2010, 45(3): 511−530.

[5] BOGUSKI B, KAHRAMAN A, NISHINO T A. New method to measure planet load sharing and sun gear radial orbit of planetary gear sets[J]. Journal of Mechanical Design, 2012, 134(1): 1002−1007.

[6] FOX G P, JALLAT E. Epicyclic gear system: US6994651[P]. 2006−02−07.

[7] FOX G P, JALLAT E. Use of the integrated flexpin bearing for improvement of the performance of epicyclical gear systems[C]// Asme International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Portland, USA: SAE Paper, 2003, 4(4): 1003−1011.

[8] MONTESTRUC A N. A numerical approach to calculation of load sharing in planetary gear drives[J]. Journal of Mechanical Design, 2010, 132: 014503-1−4.

[9] 袁茹, 王三民, 沈允文. 行星齿轮传动的动率分流动态均衡优化设计[J]. 航空动力学报, 2000, 15(4): 410−412, 418. YUAN Ru, WANG Sanmin, SHEN Yunwen. Dynamic optimum design of power shared out equally among the planetary gears[J]. Journal of Aerospace Power, 2000, 15(4): 410−412, 418.

[10] 陆俊华, 李斌, 朱如鹏. 行星齿轮传动静力学均载分析[J]. 机械科学与技术, 2005, 24(6): 702−705.LU Junhua, LI Bin, ZHU Rupeng. Analysis of static load sharing in planetary gearing[J]. Mechanical Science and Technology, 2005, 24(6): 702−705.

[11] 叶福民, 朱如鹏, 鲍和云. 非等模数非等压力角NGW型行星齿轮系静力学均载行为[J]. 中南大学学报(自然科学版), 2011, 42(7): 1960−1966. YE Fumin, ZHU Rupeng, BAO Heyun. Static load sharing behavior in ngw planetary gear train with unequal modulus and pressure angles[J]. Journal of Central South University (Science and Technology), 2011, 42(7): 1960−1966.

[12] 朱增宝, 朱如鹏, 鲍和云, 等. 偏心与齿频误差对封闭差动人字齿轮传动系统动态均载特性的影响分析[J]. 航空动力学报，2011, 26(11): 2601−2609. ZHU Zengbao, ZHU Rupeng, BAO Heyun, et al. Impact of run-out and meshing-frequency errors in dynamic load sharing for enchased differential herringbone train[J]. Journal of Aerospace Power, 2011, 26(11): 2601−2609.

[13] 朱增宝, 朱如鹏, 李应生. 安装误差对封闭差动人字齿轮传动系统动态均载特性的影响[J]. 机械工程学报, 2012, 48(3): 16−24. ZHU Zengbao, ZHU Rupeng, LI Yingsheng. Impact of installation error on dynamics load sharing characteristic of enchaced differential herringbone train[J]. Journal of Mechanical Engineering, 2012, 48(3): 16−24.

[14] 徐向阳, 朱才朝, 刘怀举, 等. 柔性销轴式风电齿轮箱行星传动均载研究[J]. 机械工程学报, 2014, 50(11): 43−49. XU Xiangyang, ZHU Caichao, LIU Huaijiu, et al. Load sharing research of planetary gear transmission system of wind turbine gearbox with flexible pins[J]. Journal of Mechanical Engineering, 2014, 50(11): 43−49.

[15] 盛冬平, 朱如鹏, 靳广虎, 等. 双排行星齿轮系统的静态均载特性行为[J]. 中南大学学报(自然科学版), 2015, 46(10): 3637−3645. SHENG Dongping, ZHU Rupeng, JIN Guanghu, et al. Study on static load sharing behavior of double-row planetary gear train[J]. Journal of Central South University (Science and Technology), 2015, 46(10): 3637−3645.

[16] 张霖霖, 朱如鹏. 啮合相位对人字齿行星齿轮传动系统均载的影响研究[J/OL]. (2017−11−27) [2018−03−28].http://www. cnki.net/kcms/detail/11.2187.TH.20171127.1536.002.html. ZHANG Linlin, ZHU Rupeng. Impact of meshing phase on load sharing for herringbone planetary train[J/OL]. (2017−11−27) [2018−03−28]. http://www.cnki.net/kcms/detail/11.2187.TH. 20171127.1536.002.html.

[17] 鲍和云, 朱如鹏. 两级星型齿轮传动静力学系统基本浮动构件浮动量分析[J]. 中南大学学报(自然科学版), 2006, 37(3): 553−557. BAO Heyun, ZHU Rupeng. Floating displacement static analysis of basic floating part of 2-stages star gear train[J]. Journal of Central South University (Science and Technology), 2006, 37(3): 553−557.

[18] KIM W, LEE J Y, CHUNG J T. Dynamic analysis for a planetary gear with time-varying pressure angles and contact ratios[J]. Journal of Sound and Vibration, 2012, 331(4): 883−901.

(编辑 刘锦伟)

Static load sharing behavior of herringbone planetary gear train with floating composite ring gear

ZHANG Linlin, ZHU Rupeng

(School of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Based on the theory of concentrated parameters, a model for analyzing the static load sharing characteristics of herringbone planetary gear transmission system with floating composite ring gear was set up. And the static load characteristic behavior theory research of the system was studied. Time-varying mesh stiffness, eccentricity error incentive and center component floating were taken into consideration. The equilibrium equations of the system load were determined by the method of Fourier series. The behaviors of static load sharing characteristics affected by the system parameters including gear eccentricity error, center component floating form and quantity, torsional stiffness of the flexible ring gear were investigated qualitatively. The results show that the system load sharing coefficient increases with the increase of eccentricity error, and the effect of component eccentricity errors in combination on the system load sharing coefficient is greater than that of component eccentricity errors alone. The torsional stiffness change of flexible ring gear affects not only the floating quantity of sun gear and ring gear, but also the system load sharing coefficient. The herringbone planetary gear transmission system with floating composite ring gear has a better load sharing effect than the normal herringbone gear planetary gear system.

herringbone; planetary gear; eccentricity error; torsional stiffness; float; static load sharing

10.11817/j.issn.1672-7207.2018.05.014

TH132

A

1672−7207(2018)05−1126−09

2017−05−09；

2017−06−25

国家自然科学基金资助项目(51375226) (Project(51375226) supported by the National Natural Science Foundation of China)

朱如鹏，教授，博士生导师，从事机械传动、结构强度和微型机械研究；E-mail: rpzhu@nuaa.edu.cn