相关系数判决的EMD在振动数据趋势项提取中的应用∗
张慧娟 李 冬
(中国人民解放军92124部队 大连 116023)
1 引言
工程测量中,由于受到各种环境因素的影响,测试信号常伴随趋势项,这严重影响时域分析和频域分析某些参数的估计精度。趋势项会产生低频峰值,淹没高频分量信息,降低频谱结果的可读性,严重时使谱分析丧失原有的物理意义。如何将数据中包含的趋势项提取的同时保证数据的可靠性和真实性,是振动数据处理的重要的研究方向之一。
试验振动数据中常见的趋势项类型可以主要概括为三种,即线性趋势项、指数型趋势项和多项式趋势项。其中对于线性趋势项提取处理最为简单,但大多数振动数据含有的趋势项较为复杂,线性方法往往难以满足需要。文献[1~4]中的方法,对指数性趋势项的提取较为准确,但由于其对低频分量较为敏感,处理时会将部分真实信号当作趋势项,造成真实信号的损失;对多项式趋势项的提取,取决于多项式的阶数,如果对多项式阶数估计不准确,会造成较大误差。经验模态分解[5~6](Empirical Mode Decomposition,EMD)是针对非平稳信号的一种有效的分解方法,在结构识别、外弹道降噪等领域得到了广泛应用[7~8]。为了得到高精度的振动数据处理结果,文中设计的方法利用经验模态分解结合对信号相关性的分析判决,提出一种适用于振动数据趋势项处理的新方法,既发挥了EMD对与被提取趋势项类型具有普适性的优点,同时考虑被提取信号的特征,保证了信号不被污染。
2 EMD基本原理和实现过程
经验模态分解(EMD)分解是将目标信号分解为若干按频率高低排列的固有模态函数(Intrinsic Mode Function,IMF)。把随机序列分解为若干固有模态函数IMF的线性组合称为IMFs,对于每个单分量信号IMF必须保证满足两个条件:1)就整个时间序列来说,极值的个数和过零点的个数必须相等或只相差1;2)在任何一点,最大值和最小值形成的上下包络线的均值为零。EMD与小波分析[9~10]相比具有无需验前选定基函数等先验信息的优点。EMD算法的基本流程为
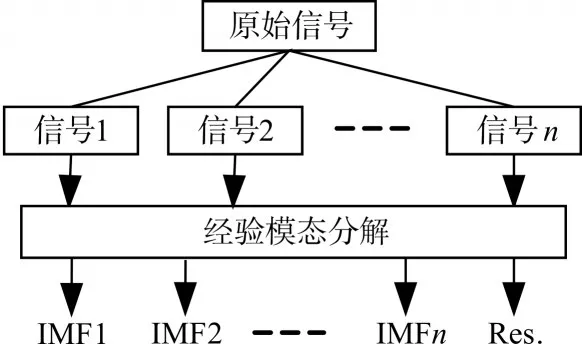
图1 EMD算法流程
设X(t)是信号的时间序列,EMD方法对信号的分解模型可概括为:通过计算,得到测试信号X(t)的所有局部极值;用三次样条函数拟合方法[11]求解测试信号中所有的极大值点构成的上包络线与所有极小值点构成的下包络线,分别记作emax(t)和emin(t);上、下包络的均值为原信号的平均包络线:m(t)=[emin(t)+emax(t)],原信号减去均值X(t)-m(t)=h(1)(t)得到新的信号h(1)(t);判断新信号是否满足IMF的两条性质。若满足,则h(1)(t)为IMF。否则,将h(1)(t)作为X(t),重复以上过程,假定经过k次分解后得到的h(k)(t)满足IMF性质,则X(t)的第一阶IMF分量就是c1(t)=h(k)(t);接下来记X1(t)=X(t)-c1(t)为原始信号,依次重复前述过程,得到第二个IMF分量,记作c2(t),余项为X2(t)=X1(t)-c2(t)。重复上述步骤,直到的余项Xm(t)是一个单调信号或Xm(t)的值无法分解为止;分解完成后,可得到m个IMFs,c1(t),c2(t),…,cm(t),最终的残余项记为Xm(t)。由于实际数据中常含有不可消除的系统误差,采用无偏估计时应注意到,对于IMFs上、下包络线均值为零的要求,显然太过严格,结合振动数据处理特性,在实际处理时,可适当放宽,只要满足包络线均值小于某个阈值ε,即可认为h(k)(t)满足IMF性质。其中ε的值,根据实际工程背景,取为ε∈[0.2,0.3]。
3 相关系数判决的EMD趋势项提取方法
相关系数又称皮氏积矩相关系数,是说明两个变量之间相关关系密切程度的统计分析指标。振动信号中包含非常丰富信息,其中真实信号与原始信号具有强相关性。大量的工程实践统计结果证明,通常在作EMD分解时,IMF分量与原信号之间的相关系数 ||ζ<0.1,认为IMF分量与真实信号基本不再具有相关性,分解得到的余项或者最低1-2阶即是信号中的趋势项,下面以仿真信号s(t)=sin(2p×20t)+sin(2p×40t)为处理对象,说明利用相关系数判决的EMD趋势项提取过程。
3.1 线性趋势项
将线性信号作为趋势项,叠加到处理对象中,构造新的待分解信号[12],得到的新信号为s(t)=sin(2p×20t)+sin(2p×40t)+x。
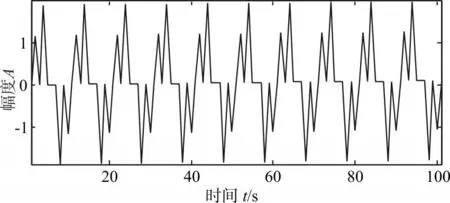
图2 含有线性趋势项的待分解信号
将混叠有线性趋势项的信号作为新的处理对象,使用EMD方法进行分解,原信号被分解为3个固有模态函数分量及余项,如图3所示。
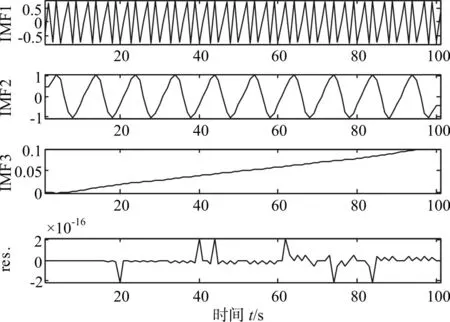
图3 EMD法分解带有线性趋势项的信号
对EMD分解后得到的每个IMF分量分别求解其相关系数矩阵,结果为
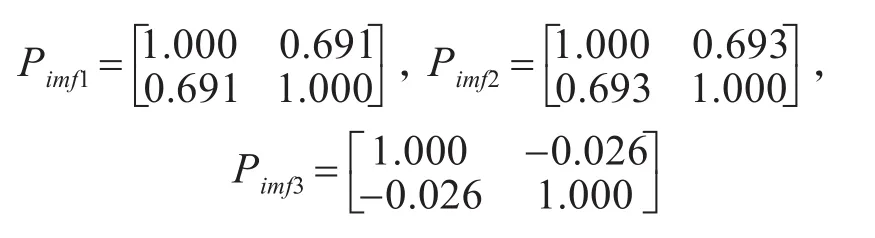
相关系数矩阵对角线上的数,即为各个IMF分量与原信号之间的相关系数,得到的结果分别是:ζi1=0.691,ζi2=0.693,ζi3=-0.026;现认为当相关系数 ||ζ≥0.1时,该IMF分量与原信号具有相关性。据此可得固有模态函数IMF1和IMF2与原信号具有较强的相关性,而IMF3与原信号之间几乎不具有相关性。因此,可认为IMF3与余项叠加后得到的信号分量就是趋势项。
将使用EMD法提取出的趋势项与仿真信号中加入的趋势项进行比较,其中用实线表示前者,而用虚线表示后者。比较的结果如图4所示。
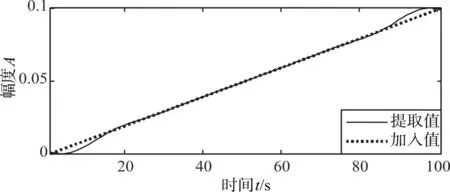
图4 比较提取结果与加入的线性扰动
使用EMD法提取出的趋势项与仿真信号中加入的线性信号作差,得到的残差如图5所示。
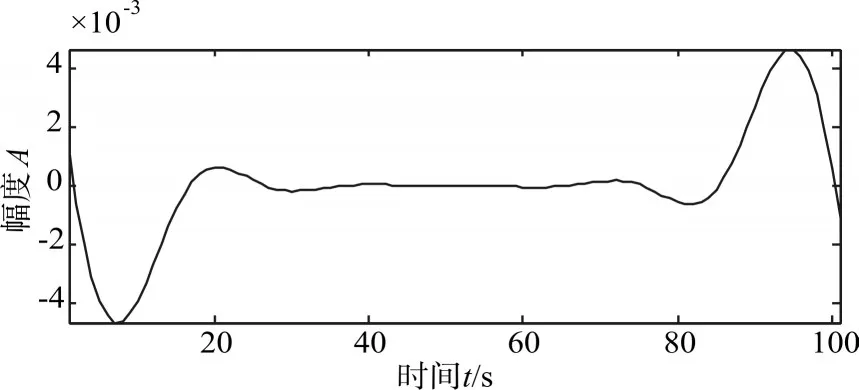
图5 提取趋势项与真实趋势项残差
3.2 指数型趋势项
仿真得到指数型趋势项,将该趋势项叠加到仿真信号中,新的信号作为待分解信号,如图6所示。
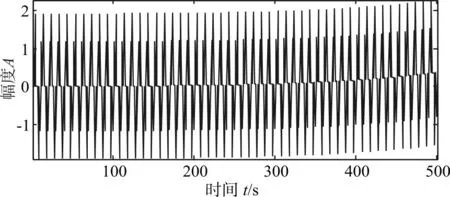
图6 含有指数型趋势项的待分解信号
使用EMD法对新的信号进行分解,分解后得到四个由高频至低频排列的IMF分量及余项,如图7所示。
分别对原信号分解得到的各个IMF分量求解其相关系数矩阵,如下:
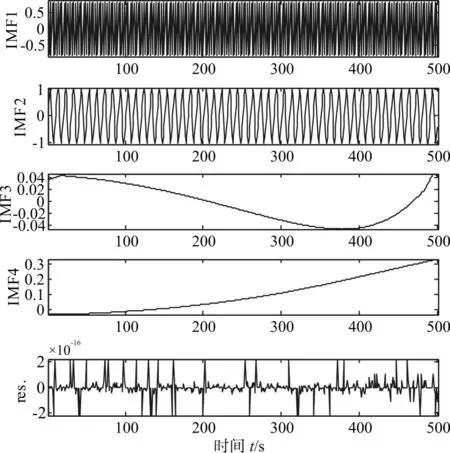
图7 分解指数型趋势项
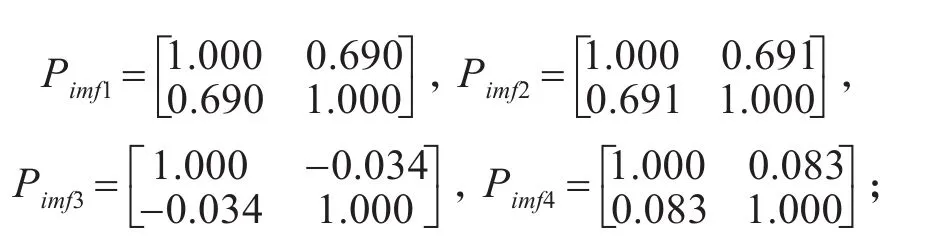
由相关系数矩阵可知,各IMF分量与原信号之间 的 相 关 系 数 为 :ζi1=0.690,ζi2=0.691,ζi3=-0.034,ζi4=0.083;根据相关系数判定趋势项的方法可知,固有模态函数分量IMF1与IMF2与原信号的相关性较强,认为是信号中的有用信息,而后两项与原信号之间相关性较弱,所以后两项与余项叠加后即认为是仿真信号中带有的趋势项,分离出的趋势项如图8所示。
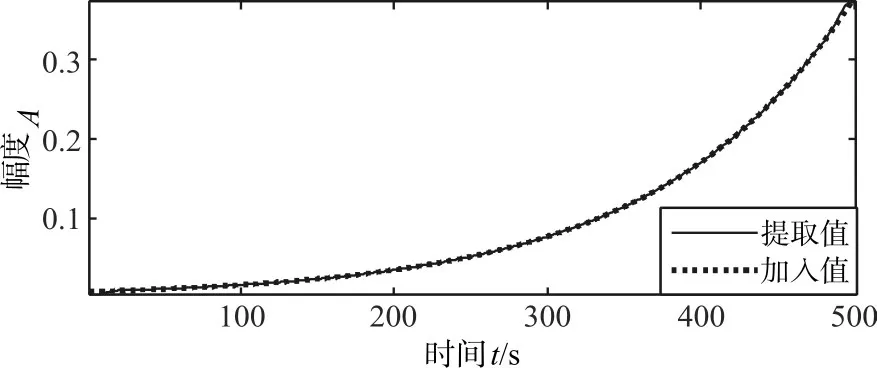
图8 比较提取结果与加入的指数型扰动
使用EMD法提取出的趋势项与仿真信号中加入的指数型趋势项作差,得到的残差如图9所示。
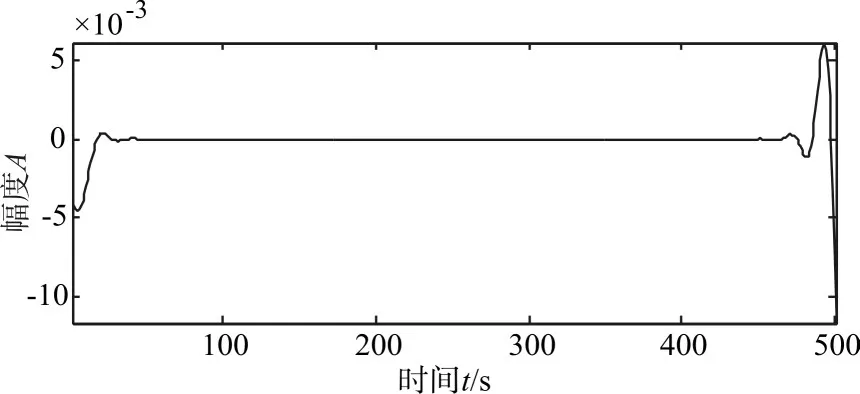
图9 提取结果与真实值残差
4 新方法提取实测数据趋势项算例分析
利用某试验中获取的一段加速度数据,对文中提出的方法加以验证,原信号的时间序列如图10所示。
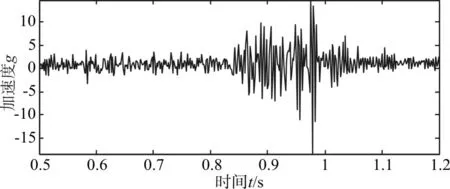
图10 某试验加速度数据片段
该信号带有未知的趋势项。首先,将对该加速度信号进行EMD分解,分解的结果如图11所示,该信号被分解为5个IMF分量和余项。现设定IMF分量与信号的相关系数阈值为0.1,认为当阈值小于0.1时,该分量与信号不具有相关性,应将其作为趋势项处理。所得到的5个IMF分量与信号的相关系数见表1。

表1 IMF分量与信号的相关系数表
由表1可知固有模态函数IMF5与待分解信号几乎不相关,因此,将IMF5以及余项叠加后,即得到趋势项。通过EMD分解,对加速度原始数据各IMF分量进行提取,本例经过5次分解成功提取出满足限定条件的频带及趋势项,如图12所示。实例表明,EMD分解是目前提取数据序列趋势项的十分有效的方法。
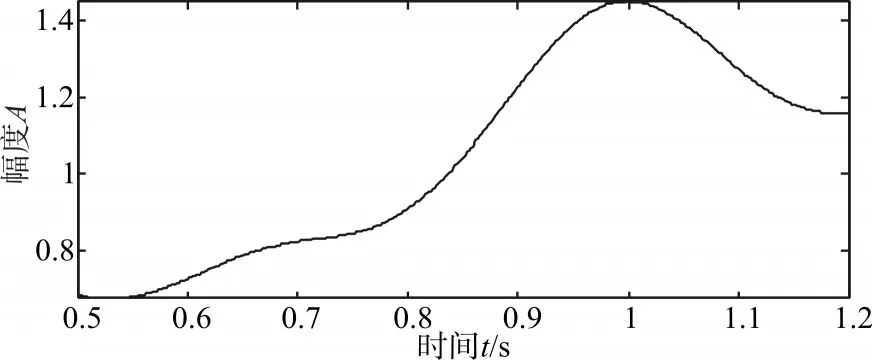
图12 趋势项提取结果
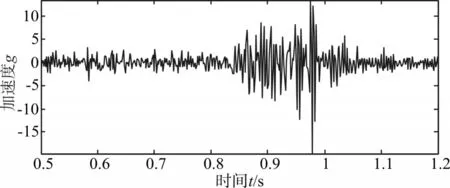
图13 去除趋势项后的真实信号
EMD方法在无需预设趋势项类型的前提下,通过自然分解的方式,从实测信号中提取出趋势项,再将剩余的部分叠加即可得到原始信号,该加速度的原始信号如图13所示,EMD方法得到的趋势项真实反映了原始测量信号的实际变化趋势。
5 结语
文中对振动数据中存在趋势项的可能性及原因进行了分析,并对利用经验模态分解提取振动数据中趋势项的方法进行了研究,仿真和实测数据计算结果证明,属于真实信号部分的IMF分量与真实信号之间具有较大相关性,而属于趋势项的IMF分量与真实信号相关性较小。因此,可设定阈值,当相关系数大于阈值时判定为真实信号分量,反之则为趋势项部分。最后将判定为趋势项的IMF分量相加得到最终趋势项。该方法能够有效地对信号中的趋势项进行提取,并尽可能保留原信号中的有用信息不受损失,保证了信号的完整性。根据算例中的信号特性,该方法可应用于外弹道测量数据的趋势项提取和遥测测量中的振动信号处理工作。
参考文献
[1]陈隽,李杰.振动信号趋势项提取的几种方法及其比较[J].福州大学学报,2005,33(s1):42-45.
[2]李慧浩,许宝杰,左云波,等.基于小波变换和EMD方法提取趋势项对比研究[J].仪器仪表与分析监测,2013(3):28-30.
[3]郭淑卿.EMD的频带滤波筛分方法[J].中国民航大学学报,2008,26(4):30-33.
[4]高品贤.趋势项对时域参数识别的影响及消除[J].振动、测试与诊断,1994(2):20-26.
[5]Huang N E,Shen Z,Long S R.A NEW VIEW OF NON⁃LINEAR WATER WAVES:The Hilbert Spectrum1[J].Annual Review of Fluid Mechanics,1999,31(1):417-457.
[6]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings Math⁃ematical Physical&Engineering Sciences,1998,454(1971):903-995.
[7]郭小红,徐小辉,赵树强.基于经验模态分解的外弹道降噪方法及应用[J]. 宇航学报,2008,29(4):1272-1275.
[8]李振兴.结合经验模态分解的振动信号趋势项提取方法[J].飞行器测控学报,2011,30(1):56-60.
[9]秦品乐,林焰,陈明.基于平移不变小波阈值算法的经验模态分解方法[J]. 仪器仪表学报,2008,29(12):2637-2641.
[10]马社祥,刘贵忠,曾召华.基于小波分析的非平稳时间序列分析与预测[J].系统工程学报,2000,51(4):305-311.
[11]Deering R,Kaiser J F.The use of a masking signal to im⁃prove empirical mode decomposition[C]//IEEE Interna⁃tional Conference on Acoustics,Speech,and Signal Pro⁃cessing,2005.Proceedings.IEEE,2005(4):485-488.
[12]费业泰.误差理论与数据处理[M].机械工业出版社,2015.

