筒口气泡对发射筒盖影响数值计算与分析∗

李智生 赵 欣 王红萍

（1.91550部队 大连 116023）（2.大连大学信息工程学院 大连 116066）

1 引言

在水下航行体出筒的过程中，发射筒筒盖还反复地受到高温高速燃气流和紊乱的水流场即筒口气泡的混合作用，其结构强度不仅关系到整个发射筒的使用寿命，对发射性能也有一定的影响，同时也影响到发射平台后续航行的稳定性、隐蔽性和安全性，甚至它还可能成为水下航行体发射时的严重障碍，直接关系到发射的成败与否。

对于筒口气泡与筒盖受载的研究方面，文献［1］针对潜射模拟弹筒口引力场进行了仿真计算，重点研究了筒盖在固定角度情况下的受载特性。文献［1～2］利用计算流体技术和试验方法对发射筒盖进行了数值模拟和试验，研究结果表明通过合理配置发射筒前后易碎盖开盖条件，可保证发射筒盖的正常开启。文献［3～4］运用最小二乘法给出了计算筒盖最大载荷及载荷力矩的经验公式，能在一定程度上预示筒盖受到的最大载荷及载荷力矩。文献［6～7］研究了轴载对航行体梁模型横向振动频率的影响，并以某型号潜地导弹发射过程中某时刻为例，用大型有限元软件ANSYS对这种影响作了计算。

在水下航行体发射出筒时，首先打开发射装置的筒盖，并使筒盖固定在一定的开角位置，使得筒口外的形状不对称，形状不对称对整个流场将产生一定的影响。其次，筒盖受筒口高压燃气射流的膨胀和收缩，筒盖将会顺应作用载荷而产生相应的变形，这种变形效果也会在一定程度上对筒盖产生卸载作用。针对上述问题，建立筒盖受力模型，使筒盖在受筒口气泡影响及受力后能在一定的范围内来回地摆动，同时利用fluent建立筒盖三维轴对称模型，计算并分析筒口气泡演化过程对筒盖影响。其研究方法可为筒口压力场预测及筒盖设计提供指导。

2 控制方程

1）航行体运动学方程

将航行体的发射过程简化为一维直线运动［8］，航行体受到的力主要有发射筒高压燃气弹射力F，自身重力G，航行体轴向阻力f（主要由水的压差阻力和粘性阻力构成）。航行体的运动方程为［9～10］

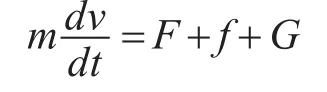
式中：m为航行体质量；v为航行体运动速度。

利用欧拉积分计算每一时间步的航行体速度和位移，更新网格信息，进行下一时间步计算。通过不断迭代计算，求得航行体的运动参数。

2）筒盖运动学方程

筒盖的运动是绕轴承基座转轴的旋转运动，本次研究的对象-筒盖简化为刚体，则筒盖及其支撑系统就可以简化为一个受激励作用的扭簧振子，设Izz为筒盖绕轴承基座铰链轴的转动惯量，Mz为流场作用于筒盖上的力矩（绕轴承基座转轴），K为筒盖系统的支撑刚度，α为筒盖转动的角度，则刚体运动的控制方程为［10～11］

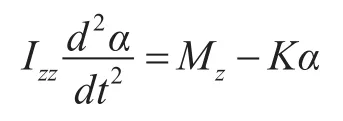
筒盖运动通过以上方程在UDF中编写相应程序实现，并设置适当的网格重构和光顺滑准则参数来控制计算。

仿真计算工质假设为粘性可压缩气体，忽略燃气与管壁之间的传热因素，海水假设为不可压流体，工质气体溢出筒外后，气泡表面与海水界面采用VOF（流体体积）方法进行跟踪。

3 模型建立

3.1 计算区域及网格划分

建立如图1所示含筒盖的发射系统，忽略了筒盖和发射筒之间连接的铰支等细节，仅建模筒盖整体结构，筒盖的转动通过动网格技术中的局部重构（Local remeshing）和弹性光顺滑（Spring Smoothing）来实现。

XY坐标轴是Fluent提供的全局坐标系，为了简便起见，在输出筒盖受载时，先输出XY坐标轴下X和Y方向上的受力，然后再折算到如图1所示的Fx和Fy方向进行分析。

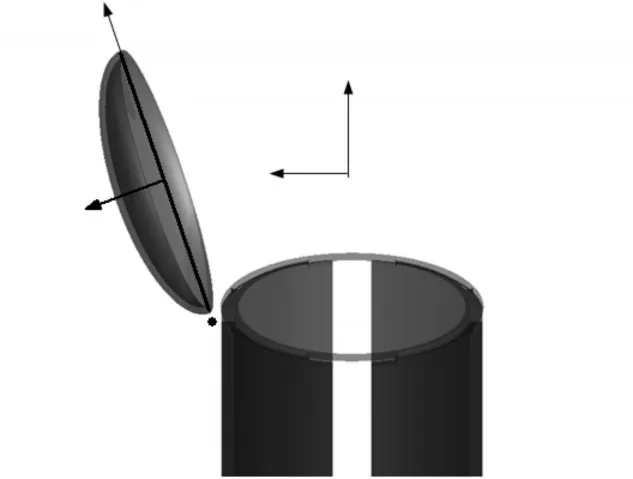
图1 考虑筒盖模型示意图

计算模型取的是关于XY平面对称，所以在Z方向上相互抵消，在Z方向上的实际受力为零，在本文中不予考虑。

图2为筒盖部分的网格划分细节，图2（a）为筒盖与对称面相交处的对称面网格，图2（b）为筒盖表面的网格划分。

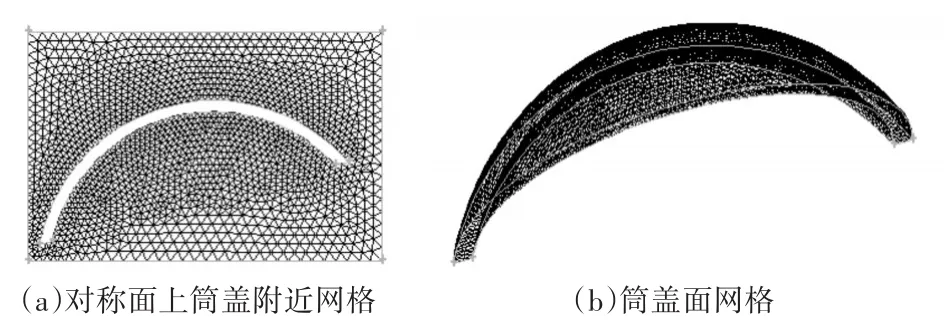
图2 筒盖部分的网格划分

整个计算域中网格足够细密，使计算结果不存在网格依赖性，大部分的网格采用四边形结构化网格。由于筒盖的复杂外形，在这一部分进行网格划分时，选择一个能包容筒盖的区域，使这一区域与外界保持联通。航行体出筒过程中，为保证发射筒间隙的网格质量，采用动网格策略［12］，层变区域通过Interface交界面进行数据交换，并在筒口附近进行了网格加密，保证能够准确捕捉到燃气外泄所引起的流动信息变化，尤其是密度场、压力场分布。区域外使用结构化网格，区域内使用非结构化网格以适应筒盖的外形。

数值计算选取了VOF多相流模型和K-ε湍流模型，压力-速度采用SIMPLE方法进行迭代求解。

3.2 计算设置

筒口气泡并不是一个自由发展的气泡，其形态演变往往受限于筒口发射平台壁面和弹尾之间形成的有限空间，所以在航行体弹射出筒的过程中，忽略因发射平台运动而产生的侧向横流，这样航行体就简化为一维运动，采用三维模型进行计算。

计算区域选择和边界条件的参数设置如下：

1）多相流设置中，将气相设置为主相，可以达到很好的收敛性；

2）模型中要加入重力影响，即设置重力方向为X轴负向，在FLUENT设置中为Gx=-9.81m/s2；

3）流场初始化按照以下步骤进行，先对整个流场参数初始化，而后标记出发射平台外全部为水的区域，之后对此区域中Patch项给出的参数进行修正，最后进行迭代计算；

4）航行体的运动状态通过UDF结合流场情况计算得出，其初始状态的计算依据是航行体离开发射筒混合气体的余压0.72MPa、余温422K和筒外海水的状态，并按发射水深20m给定压力梯度。

4 仿真计算与结果分析

4.1 模型校验

图3为筒盖壁面测点压力测点无量纲压力随时间变化曲线，可以看出数值仿真和试验实测值的变化趋势和量级是基本一致的。筒盖处的测点压力脉动是由筒口气泡和水交互耦合所致，在一定程度上反映了筒口流场计算的准确度，仿真和试验数据的一致性表明了所用计算模型和数值算法的可信性。

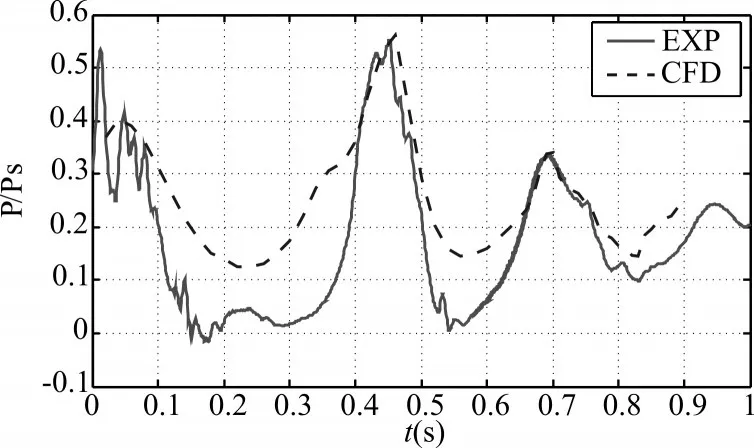
图3 压力测点无量纲压力-时间曲线

4.2 筒口气泡特性分析

图4为不同时刻，航行体出筒过程中，筒口气泡形态和压力分布云图。

从图4中可以获得以下信息：

1）筒口气泡的非定常发展过程：航行体离筒，燃气进入水介质和周围环境交互在一起，在筒口形成一个包裹航行体的燃气团，随着运动的航行体、发射平台壁面等边界生长、被穿刺和破裂；当航行体运动到一定距离，燃气泡被拉断，出现收缩-膨胀-收缩的过程，直至海水倒灌入发射筒内；

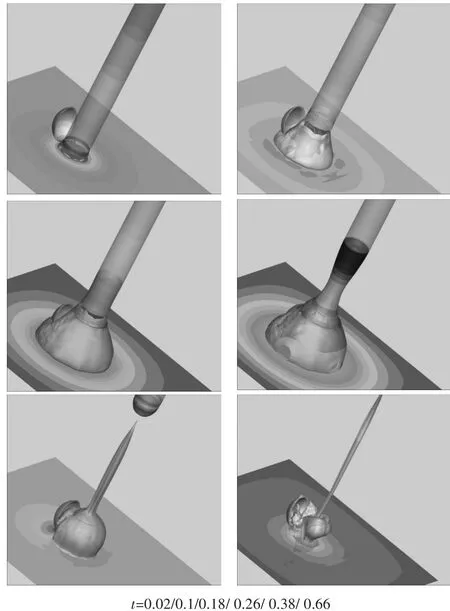
图4 筒口气泡形态及压力云图

2）气泡的弹性效应：在惯性作用下，气泡在水下形态发展呈现弹性效应，即周期性地膨胀和收缩，导致泡内压力周期性变化；弹尾离筒时，筒口附近区域处于高压状态，由于筒盖系统的存在，筒口周围燃气泡出现不对称现象，导致筒盖内侧先开始受到燃气泡的扰动；由于筒盖系统的存在阻尼力，受载逐渐增大，当受载扭矩超过阻尼力，筒盖开始向背离航行体的方向运动，筒盖内侧受到的压力降低，如图4中t=0.18s；当筒口气泡膨胀到一定体积后，甚至将筒盖覆盖，其后泡内压力降低，受到当地水压的作用开始收缩，筒盖由于惯性还要继续运动一定角度，后开始减速，筒口附近的燃气泡，航行体离筒后会一直持续膨胀-收缩的过程，筒盖伴随出现在开盖角度位置往复运动。

4.3 筒盖受载特性

在UDF中编写了筒盖运动的控制方程，同时将其运动参数和动力参数输出来分析其运动规律。

图5给出了筒盖摆动角度及角速度与时间的变化规律，结果表明：摆动角度和角速度规律基本呈正弦函数，摆动频率在2Hz～4Hz之间。筒口气泡第一次膨胀，在t=0.14s时刻，筒盖最大摆动角度为6.19°；在下一次的收缩过程中，在t=0.43s时刻，筒盖最大摆动角度为-9°，筒口在随后的膨胀与收缩中，筒盖的摆动角度幅度为±12°左右，是由于在t=0.5s后，弹尾燃气泡断裂的冲击和海水压力的作用对筒盖的运动受到影响。

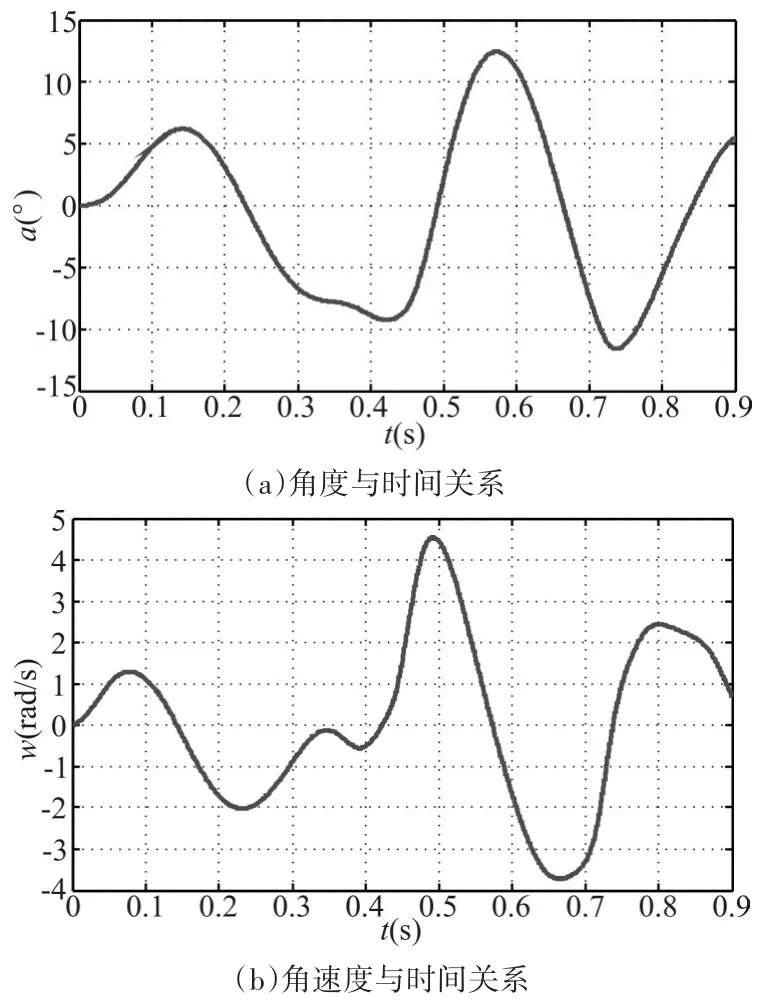
图5 筒盖摆动角度及角速度与时间变化曲线

由于气泡附着在筒盖的内外表面，气泡的压力变化会影响到筒盖受载，图6为筒盖在X和Y方向的受载力以及铰支力矩随时间的变化曲线。

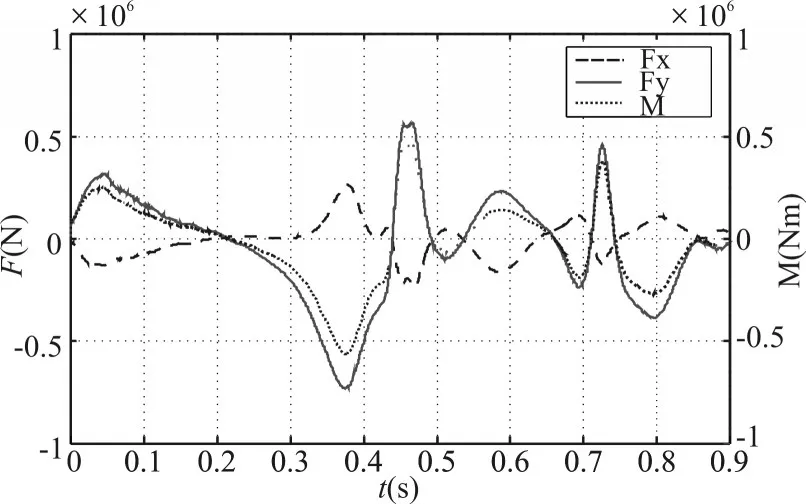
图6 筒盖受载与时间关系

由图6可以看出：

1）发射过程中筒盖经受了多次正负受载，受载的主要方向是在垂直于筒盖的方向，筒盖受载随着气泡形态的变化而变化，在发射初期产生了剧烈的正向脉冲；当筒盖开始运动后，压力逐渐减小，最大值出现在流场燃气泡第一次收缩和第二次膨胀阶段；

2）筒盖受载同样来源于筒口气泡和水介质的交互作用，气泡内压升高时造成正峰值，降低形成负峰值；

3）筒盖受力和力矩变化趋势基本一致，仅在局部存在差异，说明压心位置未发生较大的变化。

4.4 速度影响分析

不同的出筒速度对筒口气泡的发展规律不同，而筒口气泡的非定常发展又会对筒盖的运动造成影响。下面以出筒速度为36m/s、33m/s、30m/s为例，分析不同出筒速度对筒盖的影响。

如图7为不同出筒速度下筒盖运动参数变化曲线，图8为不同出筒速度下筒盖受载情况，图中横坐标为航行体位移。

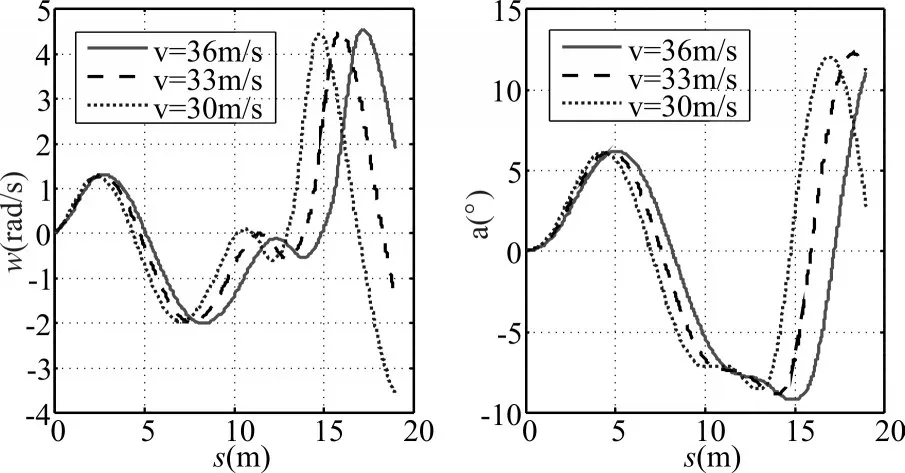
图7 筒盖的运动参数与位移关系

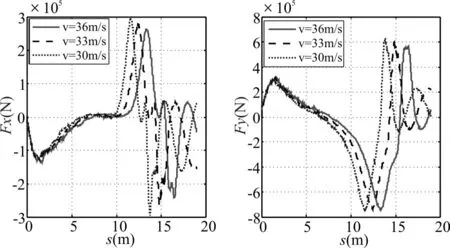
图8 筒盖受载与位移关系

由图7和图8可以看出：

1）航行体离筒初期，即位移2m前，出筒速度对筒盖的运动规律和受载特性影响很小；弹动位移到达4m以后，出筒速度越大，筒盖摆动角度越大，但是筒盖在X方向的受力影响变化不大，主要在Y方向的受力；在弹动位移达到10m以后，筒盖受载变化规矩基本一致，只是在相位上有差别，速度越大，受载越滞后；

2）筒盖受载来源于筒口气泡和水介质的交互作用，气泡内压力升高时造成正峰值，降低形成负峰值。

以上分析表明在发射过程中由于筒口气泡演变的扰动，筒盖承受了相当程度的扰动，且受载方向存在周期性变化特性。

5 结语

本文基于VOF模型、动网格技术及三维轴对称模型，建立了筒盖受力变形和卸载条件下的运动模型，仿真得到的筒盖压强量值与实测数据基本吻合，表明所建模型可在工程范围内用来模拟筒口气泡与筒盖受载的特性。在此基础上研究了筒口流场特性及对筒盖载荷的影响，并对比分析了不同出筒速度条件下的筒盖受载特性；结果表明，在发射过程中由于筒口气泡演变，筒盖承受了相当程度的扰动，且受载方向存在周期性变化特性。研究方法及其结论可为发射筒筒口压力场预测以及筒盖设计提供有益的指导。

参考文献

［1］王汉平，吴菊华.基于CFD的潜射导弹筒口压力场预测［J］.弹道学报，2008，20（4）：73-76.

［2］尚书聪，孙建中.基于筒口气幕环境的导弹出筒过程受力影响研究［J］.哈尔滨工程大学学报，2012，33（11：1-6.

［3］姜毅，耿锋，张强.导弹发射筒盖开启过程数值计算及试验［J］.弹道学报，2008，77（03）：33-35.

［4］胡仁海，倪火才，陈军峰.燃气后效对发射体影响研究［J］.导弹与航天运载技术，2012，321（5）：11-14.

［5］方国强，杨为，李晓晖.一种筒盖系统载荷计算方法［J］.舰船科学技术，2011，33（10）：63-66.

［6］王英华.轴向载荷对潜射导弹横向振动特性影响分析［J］.导弹与航天运载技术，2002，311（06）：9-15.

［7］殷崇一.潜射导弹发射与出水载荷研究［D］.西安：西北工业大学，2004.

［8］崔可.航行体出筒以及水下运动的水动力研究［D］.哈尔滨：哈尔滨工业大学，2012.

［9］胡海龙.无动力水下运载器的动力学建模与仿真分析［D］.哈尔滨工业大学，2010.

［10］祁晓斌，王瑞，袁绪龙.水下垂直发射燃气后效对筒盖系统的影响研究［J］. 兵工学报，2017，38（11）：2184-2189.

［11］李杰，鲁传敬.潜射导弹尾部燃气后效建模及数值模拟［J］.弹道学报，2009，21（04）：6-8.

［12］曹嘉怡，鲁传敬，李杰.潜射导弹水下垂直自抛发射过程研究［J］.水动力学研究与进展（A辑），2006，21（06）：752-759.