基于改进EMD算法的水下潜艇磁异常信号处理分析∗

孙华庆 王 丹

（海军潜艇学院 青岛 266000）

1 引言

磁探测系统是对潜艇声纳探测的有效补充，可实现对潜艇目标的高精度定位。针对复杂信号常见的非平稳性、非线性特点，美国华裔Huang等在1998年提出了具有创新性的信号处理方法——经验模态分解方法（Empirical Mode Decomposition，EMD）［1～2］。

EMD算法对磁异常信号的处理基本能达到从强噪声信号中提取目标信号的目的，但是对于本身磁异常信号强度弱、背景噪声信号频带较宽的情况提取有一定误差。主要原因是IMF分解不正常，称模态混叠现象［3］，该现象有两种情况，一种是一个IMF中包含着差异极大的时间特征尺度，另外一种是相近的特征时间尺度分布在不同的IMF中，会导致IMF波形不能真实反映该频率的波形或相邻的两个IMF存在波形混叠现象。这种现象和输入信号特征有关，特别是非线性非平稳的脉冲信号、间歇信号及含高斯噪声信号。

为解决这一模态混叠现象，Wu等在2009年提出了总体平均经验模态分解算法（Ensemble Empir⁃ical Mode Decomposition，EEMD）［4］。Wu利用高斯白噪声的特点，在含噪信号中加入高斯白噪声信号，对该合成信号EMD分解出IMF后，再重复向原始信号中加入不同的高斯噪声进行EMD分解，在多次重复加噪分解后进行标准化平均，恢复原数据分布大小。

在EEMD过程中，对原始信号加入高斯噪声能够改变信号中极值点位置及幅值，从而在IMF分解前改变上下包络线的形态，在提取的低阶分量中可以把原有信号噪声、添加的高斯噪声和部分信号中可能存在的间歇信号分离出来［5～6］。

对经验模态分解算法的分析中，CEEMD相对于另外两种更加优化，但是在IMF分量重构的过程中，需要考虑如何确定滤除低频分量的阶数。滤掉的分量多，重构信号平滑性好，没有噪声的干扰，但目标信号有遗失；滤掉分量少，信号保存较完整，但是噪声干扰太大目标信号特征无法提取。在分量选择过程中，需要对两个指标进行平衡优化，根据原始信号的特点及选择最合适的分解阶数。

2 潜艇磁异常信号仿真

当磁探仪与目标位置点距离大于2.5倍的磁性目标长度时，该目标可以视为一个磁偶极子［7］。距离磁性目标r(x,y,z)处的磁场可表示为

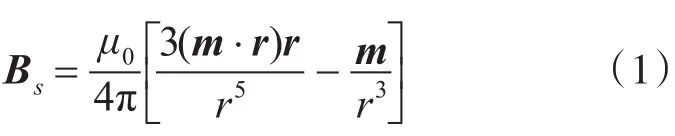
式中：m(mx,my,mz)为潜艇的磁矩，μ0为真空磁导率，r= ||r为潜艇到磁探仪的距离［8］。

仿真假设条件如下，在水深200m的某试验海区，在地磁坐标系中，设试验海域为半径500m的圆形，潜艇位于海域中心，速度为4m/s。距离海底50m。设某潜艇磁矩

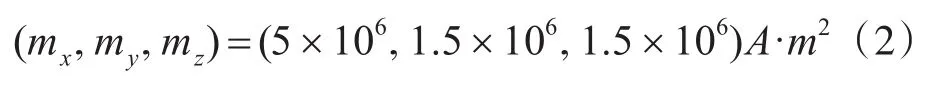
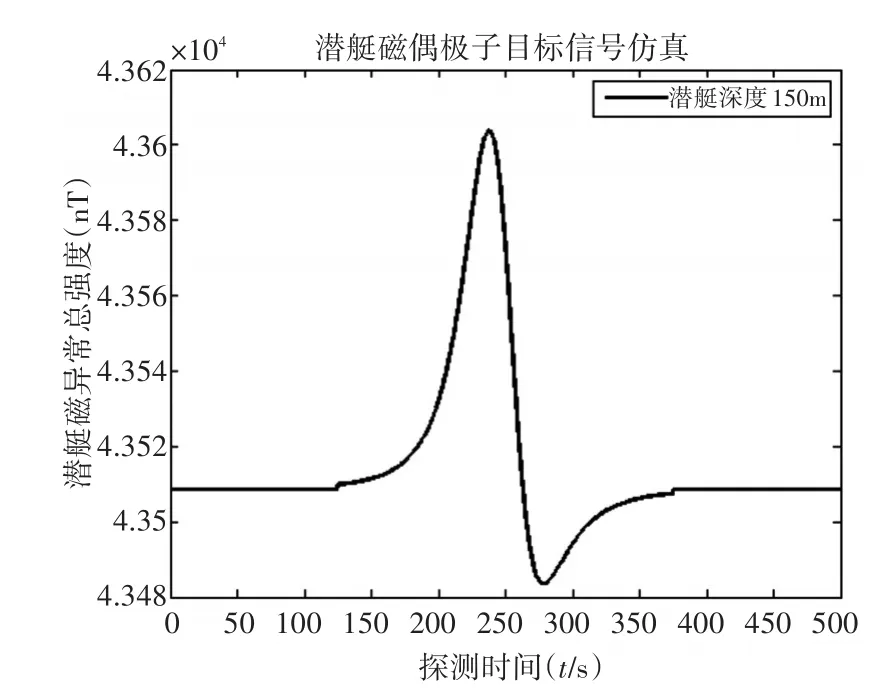
图1 原始目标信号仿真图

在上述原始目标信号的基础上添加信噪比-20dB高斯白噪声，这种情况下，潜艇磁异常信号基本淹没在背景噪声中，无法从时域信号中分辨出信号的特征甚至不能发现潜艇信号存在。

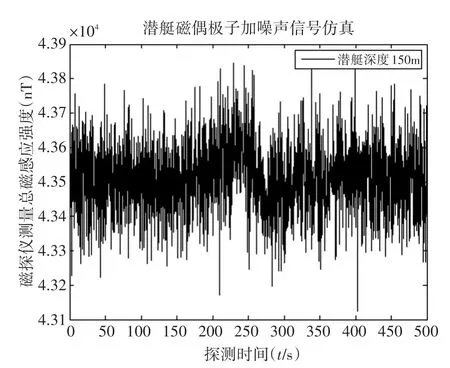
图2 加噪信号仿真图

3 EEMD算法信号处理

信号迭代过程中，计算前后数据的标准偏差（Standard Deviation，SD），若标准偏差小于某一预设阈值，则停止。信号分解表达式为

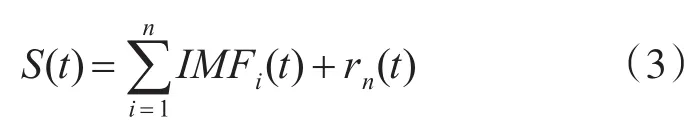
图3是对加噪信号进行EEMD分解的结果。从结果可以看到，共进行了11阶的分解，得到11个IMF分量。第一阶IMF1和第二阶IMF2基本全是高频的高斯噪声，信号信息基本分辨不出；从第三阶IMF3开始，磁异常信号逐渐显示出来，特别是到了第五阶IMF5，噪声基本消失，磁异常信号在该层的分离胶明显，和原始信号曲线的变化趋势类似；到第十一阶IMF11，信号逐渐失真，向单调曲线变化，说明磁异常信号在这个阶层的频率上很少；最后是余项Res，余项基本成为一条单调曲线，无法获取信号的信息。

由EEMD的IMF分解结果可知，如在IMF3中，EEMD的极值点分布更均匀，说明EEMD算法达到了均化极值点分布的目的，经过数次平均，减少添加的噪声的影响，从而减小了模态混叠效应。

4 最优降噪算法推导

青岛理工大学的郑一教授针对随钻钻井液脉冲信号容易受噪声干扰的特点，利用EEMD算法将信号分解不同的固有模态函数，进行降噪滤波，对脉冲信号方波整形处理，引入“影响因子”的概念，综合考虑重构信号的逼近度和相关度。该方法对钻井液脉冲信号的处理的结果合理有效［9］。

基于EEMD的最优降噪算法，针对受高斯噪声污染的潜艇磁异常信号，提出建立EEMD最优降噪算法滤波器，即将高低频的分量进行按频率分离。使用两个指标进行选择最佳降噪阶数。

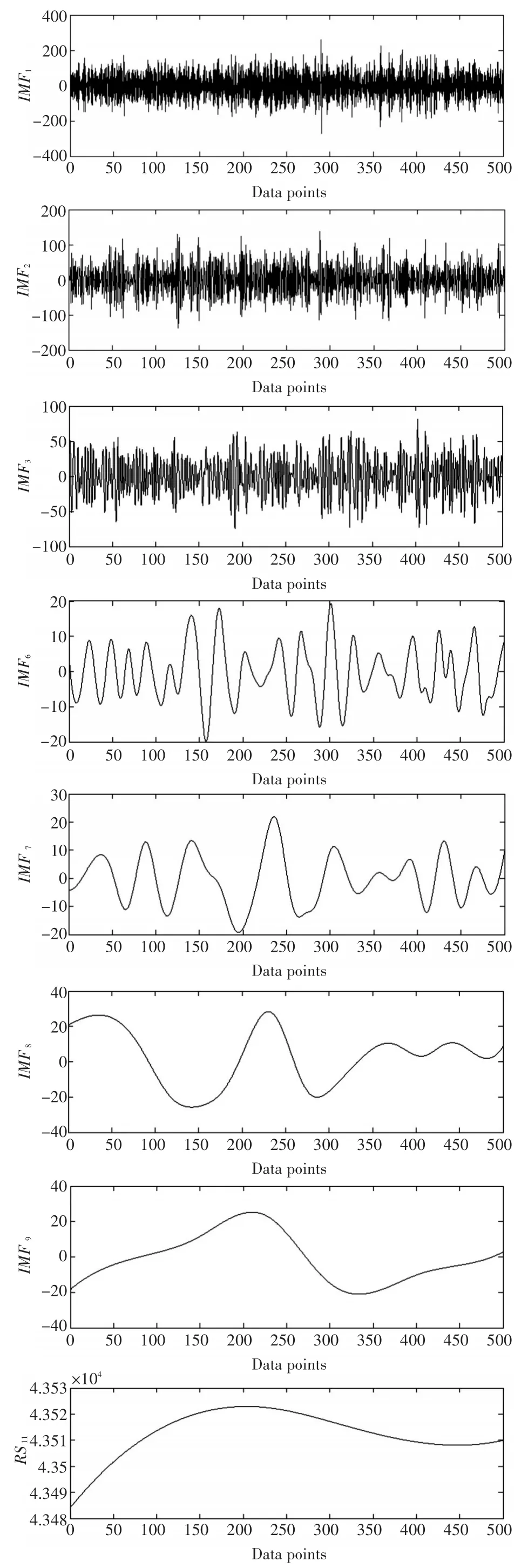
图3 EEMD分解IMF分量及Rs余项图

1）相似性指标

设磁异常信号为，将信号进行CEEMD分解，构建低通滤波器。取得n层固有模态分量IMF及最后一个剩余分量residual之和，IMF1～IMF3之和……，即

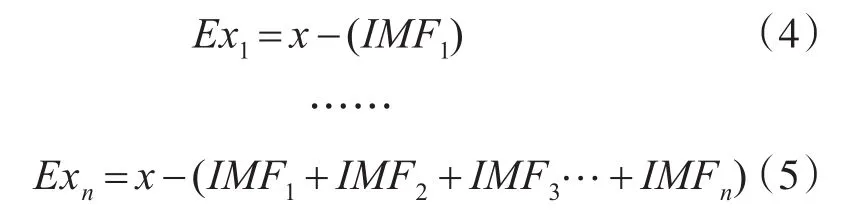
则Ex1,Ex2,Ex3,…,Exn是分离重构后的信号，该信号中依次频率降低，含噪比例依次降低，目标信号成分比例依次降低。因此需要找到一个合适的分离降噪层数，既能保证信号的相对完整性，又能尽可能多地滤掉高频信号。

为表征信号的相似性，用标准差（均方误差）进行衡量。将n个处理过的去噪信号与原始信号分别作差，得n个信号的残差，记为C1,C2,C3,…,Cn，对残差进行均方误差分析。考虑便于不同信号特征比较，统一标准，使其残差标准差指标范围在0～1之间。

残差标准差矩阵为

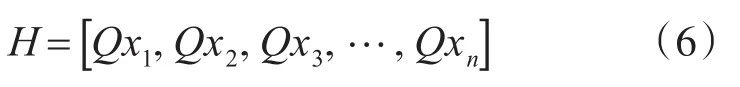
则归一化后为

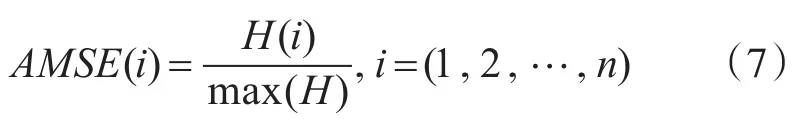
2）光滑性指标

为描述曲线的光滑性指标，将任意一段曲线在x0点分两左右段，设为P（t），Q（t），在一定步长的小区间内，P，Q的曲率越接近，说明该段的平滑性越好；如果很多一定步长连续的小区间的平滑性都较好，说明曲线整体的光滑性好。在x0点左右小区间段的曲率为

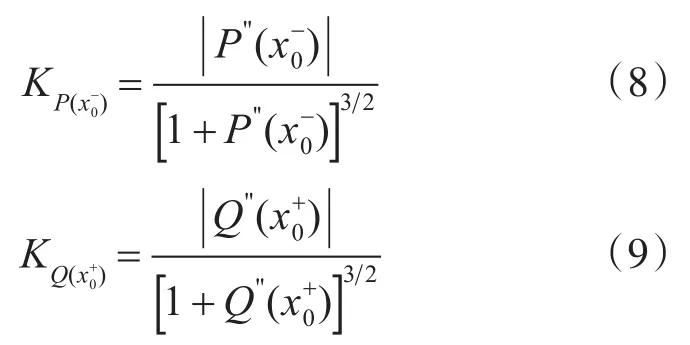
设区域取值步长为l，则

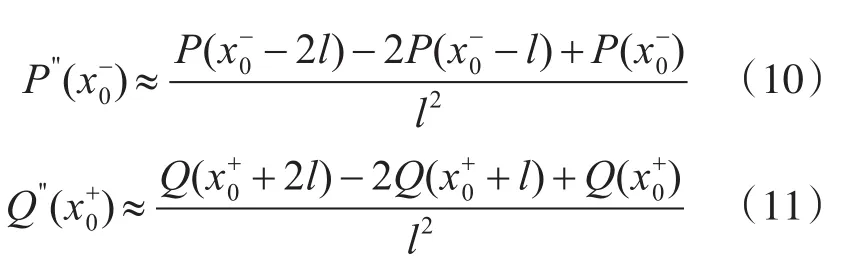
在x0点位置，定义曲线光滑度的指标计算公式：

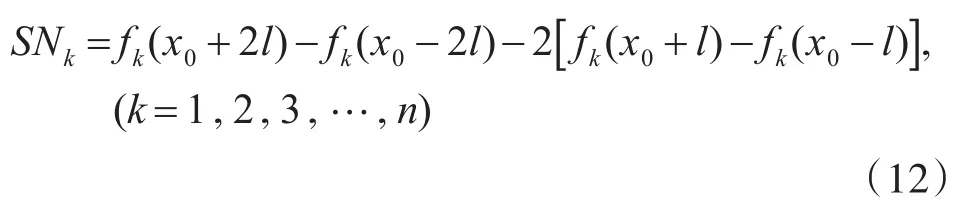
其中，对于每一条曲线

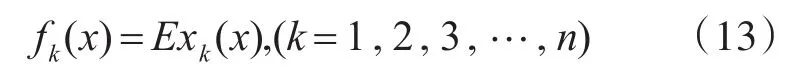
由光滑度定义可知，SN越小越接近0，说明曲线越光滑，当SN=0时，说明在x0点小区域内曲线为直线。为分析整个曲线的光滑性，设定某一间隔取x0的值，将整个曲线用多个连续的小区间表达出来，每个小区间的光滑度值集中到该曲线对应的矩阵SN中。

对每条曲线的光滑度矩阵求标准差，光滑度标准差组成的矩阵为

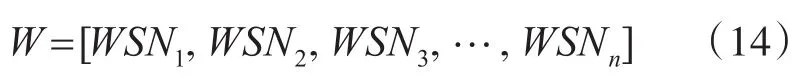
同理，为方便比较，使其光滑度标准差指标范围在0～1之间。

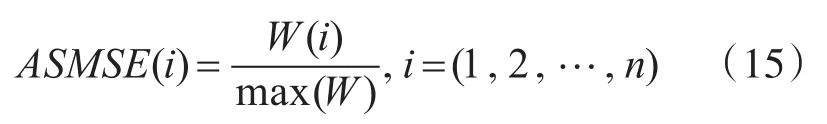
建立目标函数FM，引入权重参数α(0＜α＜1)，根据目标信号特征平衡光滑性和相似性的矛盾，进而选择最佳的降噪层数，实现复杂磁异常信号的提取。α(0＜α＜0.5)时，追求降噪信号曲线更光滑；α(0.5＜α＜1)时，追求降噪信号与目标真实信号相似性。

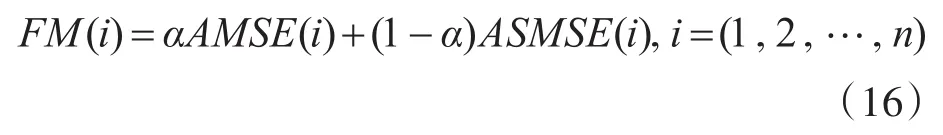
当FM取最小值时，对应的降噪阶数即最优。

5 信号分析

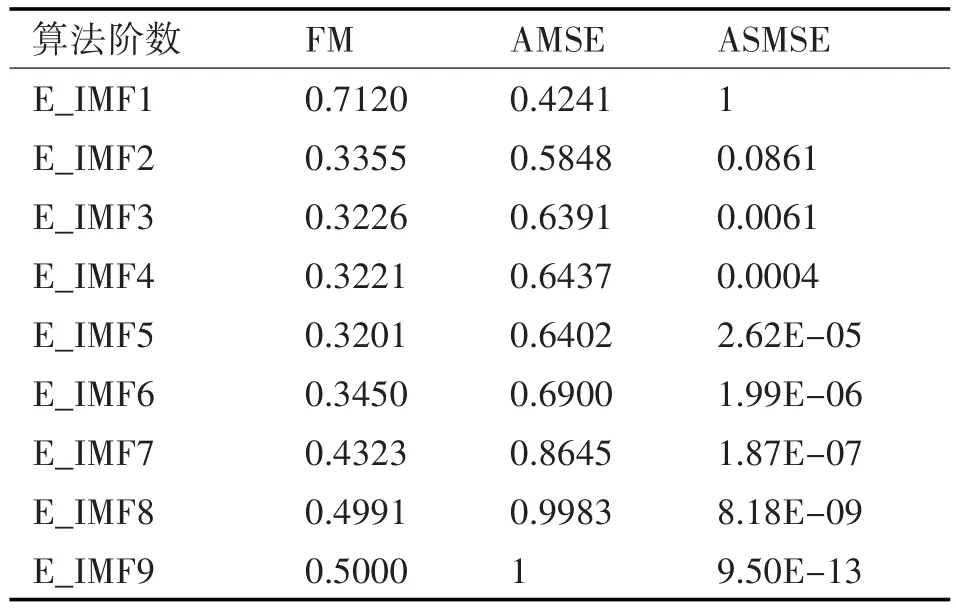
表1 优化算法指标表（α=0.5）

当α=0.5时，滤波过程中信号的平滑性和相似性同等权重，从高频到低频，随着信号重构分量减少，合成后的信号特征与目标真实信号特征相似度降低，合成信号中的噪声含量降低，曲线更加平滑，信号整体完整性降低。FM参数先降低后升高，在IMF5时取最小值，根据上节推导公式，目标函数FM取最小值0.3201时有最佳降噪阶数，即滤掉前5阶高频分量，得到的滤波信号保留了目标磁异常信号的特征，同时平滑性较好，没有噪声的干扰。

利用EEMD算法对不同阶数的信号进行重构合成，结果如下：

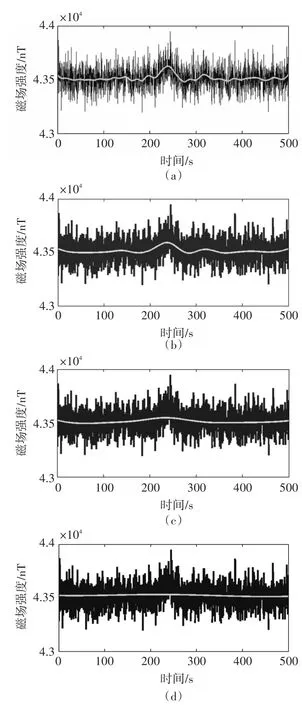
图4 不同阶数EEMD信号累加重构图

图4（a）～（d）分别代表4阶降噪到7阶降噪结果曲线与原始信号对比图。由图可知4阶降噪结果异常小突起过多，在进行磁异常信号检测时容易造成误判；第5阶降噪后曲线能够反映原始目标信号变化趋势，两侧曲线波动较小，不会对异常提取造成干扰噪声基本消失，原始目标信号特征显现出来，可以进行特征提取；第6阶降噪过于平滑，曲线无法表达原始目标信号的特征，目标信号信息丢失过多，第7阶及后重构曲线基本为一条直线，不具有借鉴意义。

利用平滑性和相似性两个指标建立目标函数，对EEMD算法的降噪阶数进行优化选择，仿真结果表明该最优降噪算法原理简单，阶数选择合适，具有一定稳定性。

6 结语

本文仿真分析了潜艇磁异常经典模型——磁偶极子模型，在潜艇磁异常信号中加入高强度噪声，利用总体平均经验模态分解算法对该信号处理。IMF分解过程中发现，噪声大部分集中在前两阶，对分解后的各层信号进行重构合成，结果基本能将潜艇磁异常特征表现出来。成对的添加高斯噪声，在抑制模态混叠的同时减小了增加噪声的影响。建立指标目标函数FM，综合考虑相似性和平滑性的基础上选择最优阶数。基于EEMD的最优降噪滤波算法对仿真数据的处理中效果较好。

本文结果表明，EEMD算法在处理强噪声干扰的磁异常的信号时，能够较好地提取目标信号特征。本文的结果对今后水下潜艇磁异常探测信号检测算法的发展有一定借鉴意义。

参考文献

［1］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlin⁃ear and non—stationary time series analysis［C］//Proc.Roy.Soc.London，1998（454）：903-995.

［2］HUANG N E，SHEN Z，LONG R S.A new view of nonlin⁃ear water waves-the Hilbert spectrum，Ann.Rev.Fluid Mech，1999（31）：417-457.

［3］GAI G H.The processing of rotor startup slgnals based on empirical mode decomposition［J］.Mechanical Systems and Signal Processing，2006（20）：225-235.

［4］WU Z H，HUANG N E.Ensemble empirical mode decom⁃position：A noise assisted data analysis method［J］.Ad⁃vances in Adaptive Data Analysis，2009（1）：1-41.

［5］YEH J R，SHIEH J S.Complementary ensemble empiri⁃cal mode decomposition：A noise enhanced data analysis method［J］，Advances in Adaptive Data Analysis，2010，2（2）：135-156.

［6］郑近德，程军圣，杨宇.改进的EEMD算法及其应用研究［J］，振动与冲击，2013，32（21）：21-26.

［7］张朝阳，肖昌汉，高俊吉，等.磁性物体磁偶极子模型试用性的试验研究［J］.应用基础与工程科学学报，2010，18（5）：862-868.

［8］单志超，曲晓慧，杨日杰，等.潜艇航向对直升机磁异探潜的影响［J］. 火力与指挥控制，2013，38（2）：62-64.

［9］郑一，孙晓峰，陈健，岳军.基于集合经验模态分解的随钻脉冲信号优良降噪整形算法［J］.石油勘探与开发，2012，39（6）：750-753.