引导学生自然地习得数学概念

余建国

【关键词】数学理解;简洁;自然;教学设计

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2018）19-0043-03

笔者认为，数学概念、原理的产生和发展应该是合理的、自然的。数学教学宜通过教师的教学设计，有意识地引导学生领悟数学思想方法，促进其数学概念的自然生长。笔者结合自己的教学、观课等实践，例谈在充分的数学理解基础上改进数学概念教学的方法。

一、类比迁移，揭示内涵生成概念

数学的发展史表明，许多数学概念具有相似的属性。类比策略在数学教学中之所以能起作用，主要是因為某些数学研究对象的本质存在相同或相似之处。对于这些概念的教学，教师可先引导学生研究已学过的概念属性，然后进行类比迁移得到新概念。

[案例1]等比数列的定义和通项公式。

教师首先引导学生回顾等差数列的定义和符号表达式，并板书。然后提出下列问题。

判断下列数列是否是等差数列：

（1）1，2，3，4，5，…;（2）-1，1，-1，1，-1，…;（3）a，a，a，a，a，…;（4）1，2，4，8，16，…;（5）1，1×（1+r），1×（1+r）2，1×（1+r）3，1×（1+r）4，…（r≠-1）。

学生一般会准确回答出（1）（3）是，（2）（4）（5）不是。

教师擦去数列（1）（3），再次抛出问题：数列（2）（4）（5）有什么特点（规律）呢？

有了熟悉的概念作铺垫，学生很快找到“比是同一个常数”的特点。此时，教师再让数列（3）显现，学生中有的说符合这个特点，有的说不符合，互相争论后统一了看法：当a≠0时也符合。于是，等比数列概念的生成水到渠成。

接下来教师只要在原来的板书上稍作改动即可进入下一个环节——推导通项公式。仍然可以采用列表类比的方法。

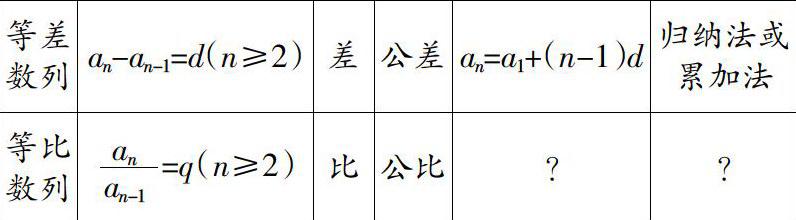
教师可以稍作提示：在等差数列中，an=a1+（n-1）d=a1+d+d+…+d，这里共有（n-1）个d相加，那么与“+”对应的运算是什么？请同学们猜想等比数列的通项公式并给出推导过程。

在教学了等差数列的定义、通项和性质的后，再让学生通过类比学习等比数列的定义、通项和性质，既可以使学生明确等比数列的学习方向和研究方法，又可以使数列知识系统化，有利于数列知识体系的构建。教学中创设联系已有相似概念的情境，引导学生利用类比方法获得新发现，并尝试给新概念下定义，这种做法顺理成章，学生易于接受。

二、遵循认知，揭示规律生成概念

奇偶性是函数的重要性质。但为什么一些函数叫“偶”函数，而另一些函数叫“奇”函数的问题，即便在学生学完本概念后仍旧会盘旋在一些学生的脑海中。江苏省特级教师陶维林的教学值得我们学习。

[案例2]函数的奇偶性。[1]

陶老师在教学中设计了下面3个问题。

问题1 画一画下列函数的图象：y=x，y=x-1，y=x2，y=x3，y=x4。请你谈谈对这些图象的感受。

问题2 对于关于y轴（或原点）对称的图象，我们反思一下刚才的列表，有何规律？

问题3 用图形计算器画出下列函数的图象：y=x5，y=x-2，y=x-3，y=x6，y=x7，给这些图象分分类？分类依据又是什么？

对这3个问题的解答，就是一个感受、发现函数数量关系和图形特征的过程。学生不难发现，一类幂指数为偶数的，图象关于y轴对称，很自然地就被叫作“偶函数”;另一类幂指数是奇数的，图象关于原点对称，也很自然地就被叫作“奇函数”。这样，奇偶函数概念的由来就清晰明了了。虽然这样的教学仅仅在幂函数范畴内做了研究，并没有给出严谨的定义，但这样的做法让学生对奇偶函数有了更多的感性认识。接下来根据列表画图的规律，抓住自变量互为相反数时，其函数值相等或互为相反数的特征，学生就能自主地给奇偶函数下严格的定义。可见，只要教师遵循认知规律，在“最近发展区”设计恰当的问题情境，教学中就能促进概念的自然生成。

三、暗藏玄机，展示联系生成概念

有效的教学是引导学生、激发学生自己去学习，帮助学生通过自己的思考建立起对数学的理解力，构建和发展数学概念，使学生的学习过程成为在教师引导下的“再创造”过程。

[案例3]平面向量的基本定理。

在学习这个定理之前，学生已经学习了“共线向量定理”：共线的向量有无数多个，在“选定一个非零向量a”的前提下，其他向量b均可用a唯一表示，即存在唯一的实数λ，使得b=λa成立。这样，共线的所有向量的运算都可以转化为向量a的运算。基于此，提出下列问题。

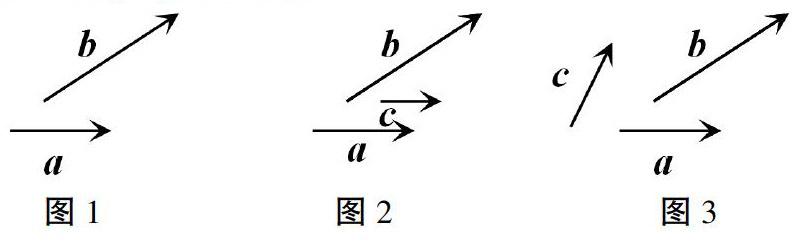
问题1 如图1，向量b能否用向量a表示？为什么？

学生会直观地看出，因为向量a、b不符合共线定理的条件，所以不能表示。也就是说，不与向量a共线的向量是不能用来表示向量a的。一个向量“不够用”，那两个向量呢？

问题2 如图2，向量b能否用向量a和向量c表示？为什么？

学生同样会发现，由于向量a和向量c共线，事实上仍然不能表示向量b。由此可见，必须选择两个不共线的向量才行。

问题3 如图3，将向量b用向量a和向量c线性表示出来。

问题4 任意向量m都可以用向量a和向量c（a与c不共线）线性表示吗？

对这个问题，学生的意见出现了分歧，有的说，零向量不能;有的说，与向量c平行的不能;还有的说，当m

问题5 如果e1，e2是同一平面内的两个不共线的向量，那么对于这一平面内的任意向量a，a=λ1e1+λ2e2的表示法是唯一的吗？

如果学生回答不唯一，那么教师可以借助“反证法”利用共线定理，说明其唯一性。当然，实际教学中，教师可以通过几何画板课件，直观地演示“任意性”和“唯一性”。

我们可以看到，在这个“引入”案例中，共线定理与基本定理是两条问题线，它们时而交汇，时而发散，在联系中完成新知识的构建。同时，学生理解了“平面向量基本定理”，也可以深化对“共线向量定理”的认识。

四、实验操作，探究分析生成概念

无论是通过教具，还是利用信息技术，数学实验都能改变学生的数学观念和数学学习方式。在数学实验中，让学生在观察、操作、探索、发现、归纳、概括等活动中完成数学概念的形成和发展，建构和完善。

[案例4]双曲线的渐近线。

圆和椭圆没有渐近线，到了双曲线怎么就“冒出”渐近线呢？根据两个实点、两个虚点，先画出对应的矩形，再画矩形的对角线，“看看这两条线，它跟双曲线有什么关系？”——这么教笔者总觉得不妥，一是结论直接告知，二是学生失去了很好的探究机会。有了几何画板，我们可以这样探究：

有学生发现，在第一象限双曲线向右上方无限伸展，且曲线逐渐“越来越直”。用什么方法體现这种“越来越”？学生思考后发现两种方法，一是将画图的定义域扩大，二是在几何画板中将“单位长1”拖小，呈现如图4。教师追问，这条线的方程是什么？

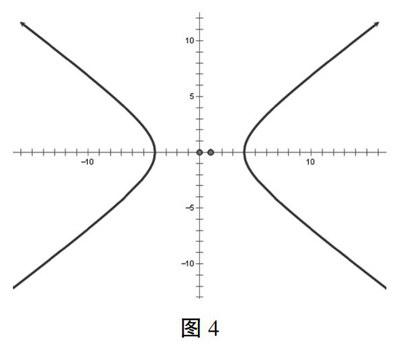
如果没有反比例函数的图象特征作为“最近发展区”，渐近线的“自然生成”是非常困难的。要实现这类数学概念的自然生成，一定要学生动手操作实验，培养学生的观察力和数学表达能力。除了真实的实验外，教师还可以充分利用现代教育技术（如图形计算器、几何画板等）设计一些实验，让学生通过实际操作学会观察、学会发现。

人民教育出版社编审章建跃老师常说，“课堂教学中，‘自然的过程来源于数学知识发生、发展过程和学生认知过程的融合，具体表现为对数学概念、原理的不断归纳和概括的过程。”[2]因此，教师首先要充分地理解数学，挖掘数学概念和原理形成过程中所蕴含的数学思想，在教学设计中，以问题为载体，通过设计有效的活动，将凝结在数学概念中的数学思维活动打开，引导学生展开学习，使数学知识的“生成”更自然，更合理。

【参考文献】

[1]陶维林.“函数的奇偶性”该怎么教[J].中小学数学：高中版，2013（11）.

[2]章建跃.课堂教学的两个关键[J].中小学数学：高中版，2008（10）.