基于VMD的振动模态固有频率识别

王江萍，常鹏飞

(西安石油大学 机械工程学院，陕西 西安 710065)

引 言

机械系统的振动信号蕴藏着丰富的状态信息，对机械系统振动模态进行分析，获得系统的模态参数，是认识机械系统动态特性设计合理与否，运行状态正常与否的关键。在机械系统的振动分析中，利用测得振动信号对机器零部件的固有频率进行识别，进而对系统固有频率进行分析，以确定故障的部位的故障诊断方法得到了广泛的应用[1]。而如何从振动信号中得到机械系统的固有频率一直以来都是国内外的一个研究热点。

实际工程中得到的机械振动响应信号一般是非平稳信号，时域识别法和频域识别法一般只能处理平稳振动信号，要识别非平稳信号，需要采用时频分析方法。典型的时频分析方法有短时傅里叶变换[2]、小波变换[3]、经验模态分解(Empirical Mode Decomposition，EMD)[4]、局部均值分解 (Local Mean Decomposition，LMD)[5]、集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)[6]等。短时傅里叶变换会产生谱泄漏，使所估计的谱值发生偏差；小波变换需要事先确定小波基，缺乏自适应性；EMD和LMD方法存在模态混叠、过包络、欠包络等一系列问题[7]。

变分模态分解(Variational Mode Decomposition,VMD)[8]是Dragomiretskiy等人于2014年提出的一种新的自适应信号分解方法，该方法在分解过程中通过循环迭代求取约束变分问题的最优解来确定分解得到的固有模态分量的频率中心及带宽，实现信号各频率成分的有效分离。与EMD和LMD相比，VMD方法具有牢固的数学理论基础，并且具有较高的运算效率及良好的噪声鲁棒性[9]。本文以悬臂梁振动加速度响应仿真信号为例，通过比较仿真结果和VMD、EMD、EEMD方法的固有频率识别结果，验证了基于VMD的固有频率识别方法的有效性。

1 变分模态分解原理

VMD将固有模态函数(IMF)定义为一个调幅-调频信号，其表达式为：

uk(t)=Ak(t)cos(φk(t))。

(1)

式中：t为时间，Ak(t)为uk(t)的瞬时幅值，φk(t)为瞬时相位函数，ωk(t)=dφk(t)，ωk(t)为uk(t)的瞬时频率。

假设多分量信号f由K个有限带宽的IMF分量uk组成，且各IMF的中心频率为ωk，VMD方法建立的约束变分模型为

(2)

uk满足

(3)

为求取上述约束变分问题的最优解，引入增广Lagrange函数，即

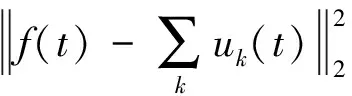
(4)

式中：α为惩罚因子；λ为Lagrange乘子。

利用交替方向乘子算法求取上述增广Lagrange函数的鞍点，即为式(3)约束变分模型的最优解，从而将f分解为K个窄带IMF分量。分解过程如下：

(2)使n=n+1，开始执行迭代循环。

(5)

(6)

(7)

(5)对于给定的判别精度ε0，若

(8)

则停止迭代，完成分解。否则重复步骤(2)至(5)。

2 VMD方法的固有频率识别

2.1 有限元建模与瞬态动力学分析

利用ANSYS软件建立如图1所示的悬臂梁模型，设置为长1 m，宽0.1 m，高0.1 m，弹性模量为2×1011Pa，密度为7 800 kg/m3，泊松比为0.3。网格边长为0.02 m，Z=0处为约束端。

瞬态动力学分析，也叫时间历程分析，是用来确定结构在随时间变化的载荷作用下的结构动力响应的方法。瞬态动力学分析可以真实地模拟结构所受载荷的情况，对研究系统的动力学特性有着重要的意义。利用ANSYS对图1模型进行瞬态动力学分析，施加阶跃载荷，集中力为-10 N，方向沿Y，分析时间为0.409 6 s，得到4 096个振动加速度与时间相对应的数据，如图2所示。

图1 悬臂梁有限元模型Fig.1 Finite element model of cantilever beam

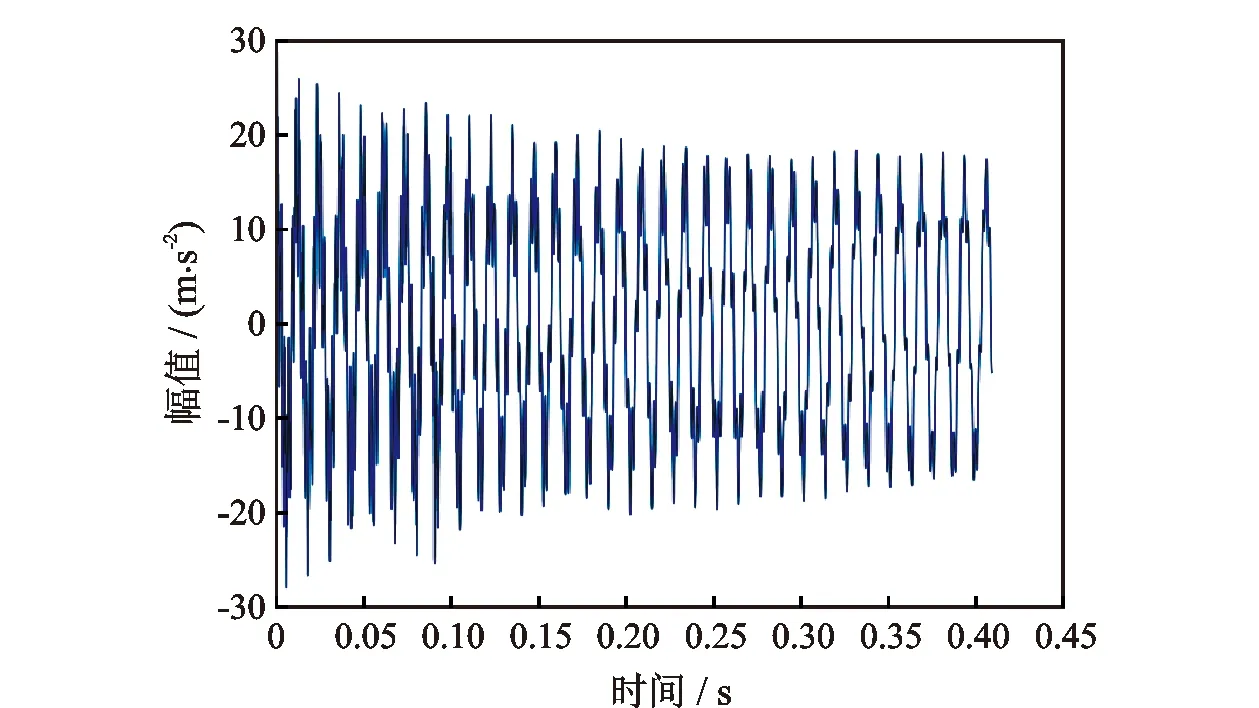
图2 原始信号Fig.2 Original signal

2.2 VMD分解与希尔伯特变换确定固有频率

利用式(5)～(8)对原始信号进行VMD分解，得到固有模态函数，固有模态函数中包含固有频率的信息，对各阶固有模态函数进行希尔伯特变换，得到对应的瞬时频率。对瞬时频率曲线进行线性拟合，可根据拟合后的直线来识别固有频率[13]，即可近似认为拟合直线的变动中心是系统的固有频率。

对IMF即u(t)作希尔伯特变换：

(9)

其中，PV代表柯西主值。

构造解析信号z(t)：

z(t)=u(t)+jH[u(t)]=a(t)ejΦ(T)。

(10)

其中，幅值函数为

(11)

相位函数为

(12)

瞬时频率函数为

(13)

VMD算法需预先设定分解模态个数，本文采用观察各模态中心频率的方法[10]，利用式(10)～(13)得到不同分解阶数时的前4阶固有频率，见表1，可以看出当分解阶数为11阶时前4阶固有频率不再变化，本文取模态个数K=11，根据文献[10-12]当α取默认值2 000时可满足大多数工况实际需求。分解得到11阶固有模态函数，图3所示为前4阶。并且得到对应的瞬时频率，如图4所示。

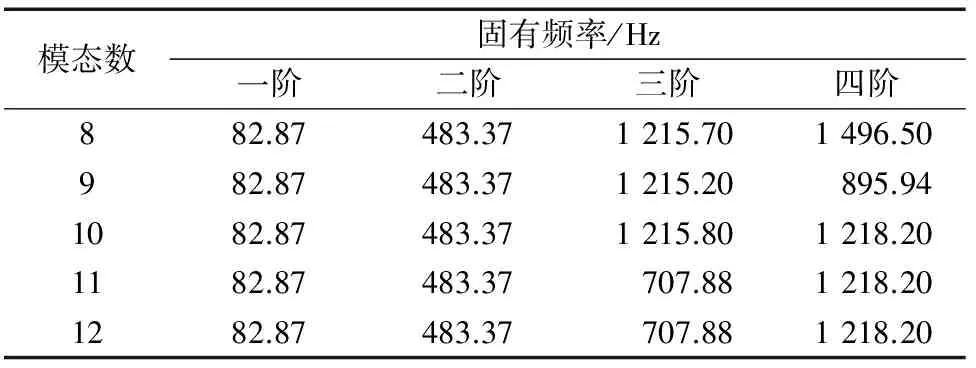
表1 VMD方法识别固有频率Tab.1 Identification of natural frequency based on VMD

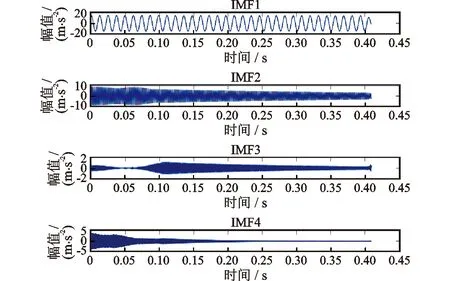
图3 VMD 固有模态函数Fig.3 VMD intrinsic mode function

图4 VMD瞬时频率Fig.4 VMD instantaneous frequency

3 基于ANSYS、EMD、EEMD方法的固有频率识别

3.1 ANSYS模态分析

模态分析用于确定设计结构或机器部件的振动特性，即结构的固有频率和振型，它们是承受动态载荷结构设计中的重要参数，常用有限元分析法仿真计算结构的固有频率。对图1所示模型利用有限元分析软件ANSYS进行模态分析，采用的分析方法是分块兰索斯法，Z=0处为固定端，可得到其前四阶固有频率，结果见表2。

表2 ANSYS模态分析计算固有频率Tab.2 Calculation of natural frequency based on ANSYS modal analysis

在求取一些模型较为简单的机械结构时，利用ANSYS软件既快捷又准确，但在实际工程中机械系统的模型往往比较复杂，难以建立，其分析结果受网格划分密集程度的影响，模型的工况约束与实际的工况约束可能不同，所以其分析结果往往是实际结构振动模态的近似。

3.2 EMD方法识别固有频率

经验模态分解(EMD)固有频率识别方法的基本思想与VMD方法有相似之处，首先对原始信号进行经验模态分解，获得IMF，对其进行希尔伯特变换，得到对应的瞬时频率曲线，最后根据曲线来识别固有频率。

EMD方法假设任何信号都是由不同的固有模态函数组成，任意两个模态函数之间是相互独立的，这样任何一个信号就可以分解为有限个固有模态函数之和，其中IMF都应满足以下条件:

(1)整个数据段内，极值点的个数和过零点的个数必须相等或最多相差一个;

(2)任意时刻，由局部极大值点形成的包络线和由局部极小值点形成的包络线的均值为零。

对相同的原始信号(图2)利用EMD进行分解，其分解过程如下:

(1)确定信号f(t)中所有的局部极值点，利用三次样条插值函数拟合形成信号f(t)的上、下包络线；

(2)将上包络线和下包络线的均值记作m1，求得：

h1=f(t)-m1。

(14)

(3)判断h1是否为IMF;若h1不满足IMF的条件，把h1作为原始数据重复步骤(1)直至满足IMF的条件。记c1为信号f(t)第1个满足IMF条件的分量，

c1=h1。

(15)

(4)将c1从f(t)中分离出来，得到

r1=f(t)-c1。

(16)

(5)将r1作为原始数据重复步骤(1)～(4)，得到信号f(t)的n个满足IMF条件的分量。所以有

(17)

当rn成为一个单调函数，不能再从中提取满足IMF条件的分量时，循环结束。则信号f(t)可表示为

(18)

其中rn称为残余函数。

对原始信号进行EMD分解可得到10阶固有模态。图5所示为前4阶。

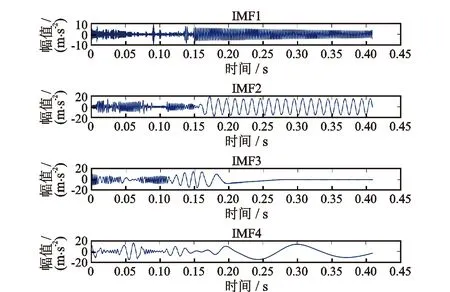
图5 EMD固有模态函数Fig.5 EMD intrinsic mode function

重复公式(9)～(13)得到前4阶固有模态瞬时频率，如图6所示。

机械系统的固有频率不随时间而变化，且频率不会为负。由于计算方法的缺陷，从图6中可见，只有0.15～0.409 6 s时间段各阶固有模态瞬时频率相对稳定且都为正值。此时间段内各阶瞬时频率对应的拟合直线变动中心即固有频率，见表3。

其中IMF1的瞬时频率计算值对应于悬臂梁的第二阶固有频率，IMF2的瞬时频率计算值对应于悬臂梁的第一阶固有频率，但IMF3及IMF4的瞬时频率得到的计算结果明显有误。

表3 EMD方法识别固有频率Tab.3 Identification of natural frequency based on EMD

图6 EMD瞬时频率Fig.6 EMD instantaneous frequency

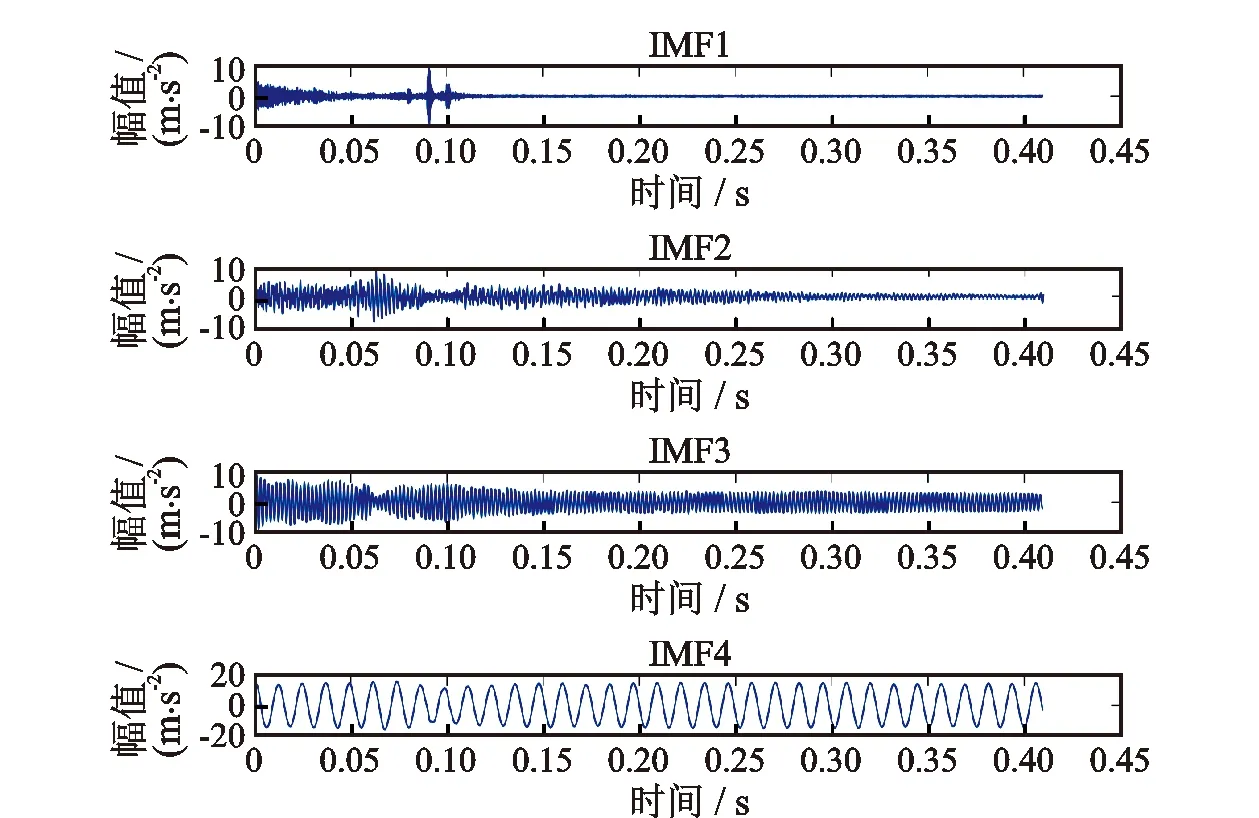
上述计算结果，符合Huang关于EMD正交性的说明[14]：分解得到的成分并不满足全局正交性，只是满足局部正交性。其实这与分解得到的IMF的性质有关，分解得到的相邻IMF成分虽然是严格按照频率从高到低产生的，但是其意思并不是说低阶IMF的频率一定比高阶IMF的高，正确的理解是低阶IMF中的某个局部的频率比高阶IMF中相同局部的频率要高，这也正好反映了EMD算法局部性强的本质所在。所以在本研究中，IMF1的瞬时频率的计算值>IMF2的瞬时频率的计算值>IMF3的瞬时频率的计算值，IMF3的瞬时频率的计算值

3.3 EEMD方法识别固有频率

EEMD是对EMD算法的改进[15]。通过在原始信号当中添加时域均值为零、频域功率谱均匀分布的白噪声，使信号具有相对均匀的极值点，保持了信号在时间尺度上的连续性，从而避免了EMD 分解中会出现的模态混叠现象[6]。其固有频率识别的基本思想与EMD方法相同。

EEMD分解过程如下:

(1)为待分析信号f(t)中加入正态分布的白噪 声，得到混合信号

fi(t)=f(t)+ni(t) (i=1,2,3，…，M) 。

(19)

(2)采用EMD分解方法对混合信号进行分析，可以得到如下相应的K个IMF分量，记为cij(t)(j=1,2,3…，K)，残余项记为ri(t)，其中cij(t)表示第i次加入高斯白噪声后分解得到的第j个IMF分量。

(3)将每次分解得到的IMF分量进行集合平均，由于加入的白噪声不相关，其统计均值为0，所以最后得到的IMF分量为

(20)

对原始信号进行EEMD分解，利用文献[16]的方法确定白噪声的幅值系数取0.1，集合平均次数M=100。可得到12阶固有模态，图7所示为前4阶。利用相同的方法对IMF进行分析，得到前4阶固有模态瞬时频率(如图8所示)，以及固有频率(见表4)，其中IMF4的瞬时频率计算值对应于悬臂梁的第一阶固有频率，IMF3的瞬时频率计算值对应于悬臂梁的第二阶固有频率。

图7 EEMD固有模态函数Fig.7 EEMD intrinsic mode function

图8 EEMD瞬时频率Fig.8 EEMD instantaneous frequency

表4 EEMD方法识别固有频率Tab.4 Identification of natural frequency based on EEMD

由于EEMD算法本身没有突破EMD算法的实质，EEMD算法中加入的白噪声是无限带宽信号，会影响原信号的频谱分布。所以EEMD方法同样有EMD方法的一些缺点，包括会出现负频率、瞬时频率波动较大、可以识别的阶数少以及IMF瞬时频率计算值的阶数与固有频率的阶数无对应关系等。

表5是各种识别方法的结果以及相较于ANSYS模态分析结果的误差。

表5 固有频率识别结果及误差Tab.5 Results and errors of identification of natural frequency using diffirent methods

由表5可以看出，基于VMD的识别方法得到的前四阶固有频率与ANSYS软件得到的结果接近，有较高的实际利用价值。而EMD与EEMD得到的结果虽然误差也较小但只能识别前两阶，实际利用价值较小。

4 结 论

(1)利用有限元分析求取结构固有频率，受模型建立、有限单元网格划分密集程度、工况约束条件设定等因素的影响，其分析结果往往是实际结构振动模态的近似。

(2)VMD方法充分利用结构工作中的振动信号，反映工程实际，计算结果较准确。VMD方法可以识别前4阶固有频率，与ANSYS的仿真结果基本一致，而且IMF瞬时频率计算值的阶数与固有频率的阶数一一对应，有较大的实际利用价值。

(3)EMD与EEMD方法虽然同样利用结构工作中的振动信号，但在识别固有频率尤其是高阶固有频率时，存在瞬时频率波动较大、会出现负值、产生模态混叠现象等问题，从而产生虚假固有频率，计算可靠性受到限制。由于其分解得到的瞬时频率由高到低，在实际工程中无法直接确定机械系统的固有频率所对应的IMF的瞬时频率计算值，所以其实际利用价值较小。

参 考 文 献：

[1] 陈雪峰，李兵，胡桥，等.基于小波有限元的裂纹故障诊断[J].西安交通大学学报，2004,38(3)：295-298.

CHEN Xuefeng,LI Bing,HU Qiao,et al.Crack fault diagnosis based on wavelet finite elements[J].Journal of Xi'an Jiaotong University,2004,38(3):295-298.

[2] 徐明远，刘增力.MATLAB仿真在信号处理中的应用[M].西安:西安电子科技大学出版社，2007.

[3] 杨福生.小波变换的工程分析与应用[M].北京：科学出版社，1999.

[4] 莫平杰，杨世锡，曹冲锋.振动模态固有频率和阻尼比的EMD识别方法[J].机电工程，2011,28(4)：392-396,428.

MO Pingjie,YANG Shixi,CAO Chongfeng.EMD method on identifying natural frequency and damping ratio of vibration mode[J].Mechanical & Electrical Engineering Magazine,2011,28(4):392-396,428.

[5] 程军圣，朱文峰，李宝庆.基于LMD的模态参数识别方法[J].计算机工程与应用，2014,51(14)：214-218.

CHENG Junsheng,ZHU Wenfeng,LI Baoqing.Method of identifying analog parameters based on LMD[J].Computer Engineering and Applications,2014,51(14):214-218.

[6] WU Z H,HUANG N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[7] 程军圣，郑近德，杨宇.一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报，2012，25(2):215-220.

CHENG Junsheng,ZHENG Jinde,YANG Yu.A nonstationary signal analysis approach:the local characteristic-scale decomposition method[J].Journal of Vibration Engineering,2012,25(2):215-220.

[8] DRAUOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Proccssing,2014，62(3):531-544.

[9] 唐贵基，王晓龙.变分模态分解方法及其在滚动轴承早期故障诊断中的应用[J]振动工程学报,2016，29(4)：638-647.

TANG Guiji,WANG Xiaolong.Variational mode decomposition method and its application on incipient fault diagnosis of rolling bearing[J].Journal of Vibration Engineering,2016，29(4)：638-647.

[10] 刘长良，武英杰，甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报，2015,35(13)：3358-3365.

LIU Changliang,WU Yingjie,ZHEN Chenggang.Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J].Proceedings of the CSEE,2015,35(13):3358-3365.

[11] 岳应娟，孙钢，蔡艳平，等.变分模态分解在轴承故障诊断中的应用[J].轴承，2016(8):50-54,65.

YUE Yingjuan，SUN Gang，CAI Yanping，et al.Application of variational mode decomposition in fault diagnosis for bearings[J].Bearing,2016 (8):50-54,65.

[12] 范磊，卫志农，李慧杰,等.基于变分模态分解和蝙蝠算法——相关向量机的短期风速区间预测[J].电力自动化设备，2017,37(1):93-100.

FAN Lei，WEI Zhinong，LI Huijie，et al.Short-term wind speed interval prediction based on VMD and BA-RVM algorithm[J].Electric Power Automation Equipment,2017,37(1):93-100.

[13] TSUKUNE H,TSUKAMOTO M,MATSUSHITA T,et al.Modular manufacturing[J].Journal of Intelligent Manufacturing,1993,4(2):163-181.

[14] 张健.关于EMD算法中模态混叠问题的分析及改进方法的研究[D].合肥：中国科学技术大学，2008.

[15] 苗晟，王威廉，姚绍文.Hilbert-Huang变换发展历程及其应用[J].电子测量与仪器学报，2014,28(8):812-818.

MIAO Sheng,WANG Weilian,YAO Shaowen.Historic development of HTT and its applications[J].Journal of Electronic Measurement and Instrument，2014,28(8):812-818.

[16] 王凤利，邢辉，邱赤东,等.基于改进自适应 EEMD 的柴油机气缸磨损诊断[J].内燃机学报,2017,35(1):89-95.

Wang Fengli，Xing Hui，Qiu Chidong，et al.Wear diagnosis of diesel cylinder liner via improved adaptive EEMD method[J].Transactions of CSICE，2017,35(1):89-95.