履带机器人越障能力优化
0 引言
在人类认识世界和探索世界的过程中,存在许多无法到达或危险的特殊场合,而随着机器人技术的不断进步,机器人越来越多地被应用到特殊极限作业环境中,机器人技术可望从根本上改变特殊作业环境下的生产作业方式[1]。
由于履带式较轮式、腿式、复合式机器人有很多移动和越障上的优势,因此履带底盘常常用于危险环境遥操作机器人中。而危险环境遥操作机器人通常会搭载上端作业设备,例如机械臂等。由于上端作业设备姿态的改变会改变履带机器人的质心位置,使履带底盘更加便于翻越障碍物,通常可以通过改变搭载的作业设备的姿态来优化越障能力[2]。但是,改变质心的同时,越障后的冲击振动也会给履带底盘及上端作业设备带来负面影响。如果不限制上端作业设备姿态改变带来的这种冲击,会给履带底盘带来一定的损失,同时减少遥操作机器人其寿命[3~5]。当上层设备为机械臂时,需要利用机械臂改变姿态优化越障能力,同时也需要将越障后对履带底盘的冲击振动影响降低[6,7]。文章根据自行设计制作的履带式机器人地盘为模型,利用Recurdyn软件的Track(LM)工具建立移动平台的虚拟样机模型并使用Recurdyn的仿真、分析功能,研究履带机器人在越障情况下机械臂姿态对越障能力的影响和改变机械臂姿态对底盘的冲击振动影响。
1 履带机器人结构
履带机器人机构如图1所示,主要结构由气体检测装置、履带移动式底盘、控制箱和三自由度机械臂组成。由于工作需要,遥操作履带机器人所搭载的气体检测装置可以在危险环境下检测气体、温度等参数,三自由度机械臂可以实现全方位移动,以及上搭载摄像机可以方便遥操作以及探查环境。履带式移动底盘需要在复杂工作环境中工作,并要求进行越障以及爬楼梯,因此履带底盘结构设计中设计了履带前角,方便履带机器人进行越障。

图1 履带机器人结构图
2 机械臂姿态对机器人越障性影响
由于机械臂可以通过改变姿态而改变履带机器人整体的质心来改善履带机器人的越障或爬楼梯性能,某些姿态对越障和爬楼梯起优化作用,但是在这些过程产生的碰撞冲击也同时会对这些姿态下的底盘和机械臂产生较大的影响。
假设履带机器人以匀速v进行越障,且越障过程中履带不脱离障碍物,履带机器人进行攀爬障碍物时受力如图2所示。
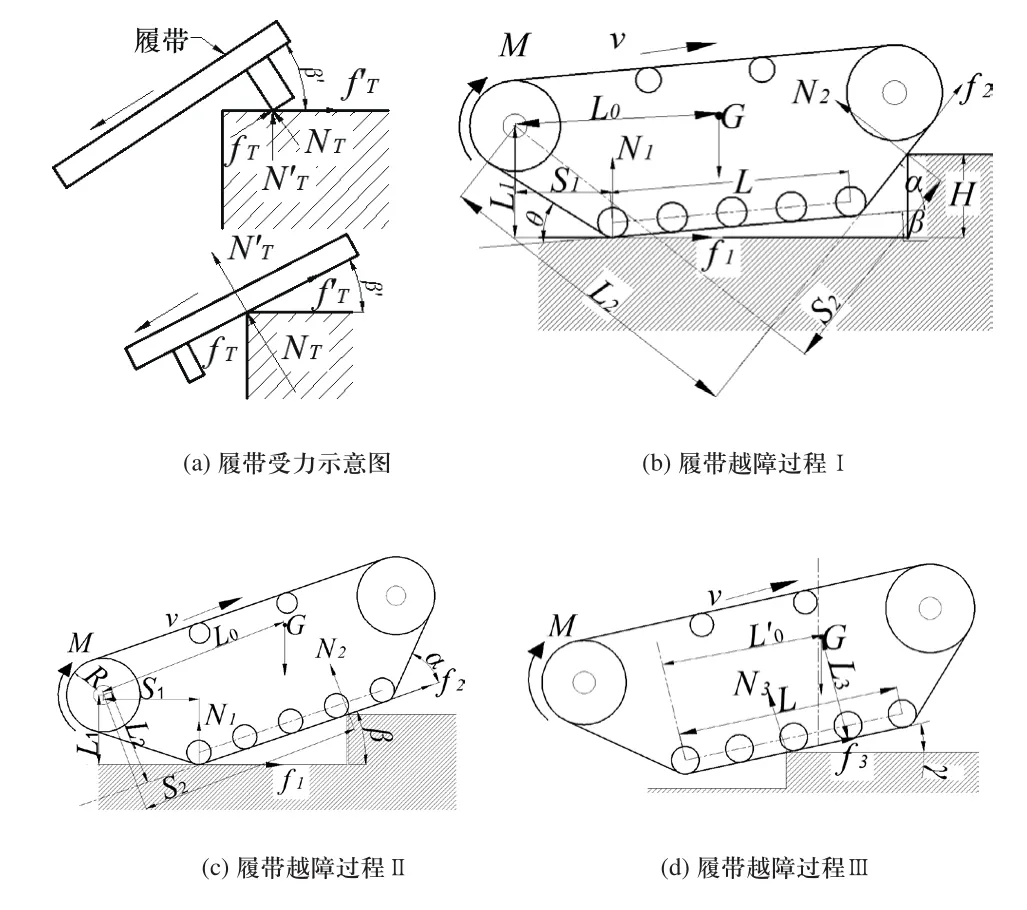
图2 履带受力分析
履带接触台阶受力如图2(a)所示,不滑移的条件为[8,9]:

式中:u为履带与地面摩擦系数;β' 为障碍物斜度;fT、NT为履带在机器人坐标系中的等效牵引力和支撑力;f'T、N'T为履带在世界坐标系中的等效牵引力和支撑力。
履带越障过程Ⅰ时受力如图2(b)所示,平衡条件为:
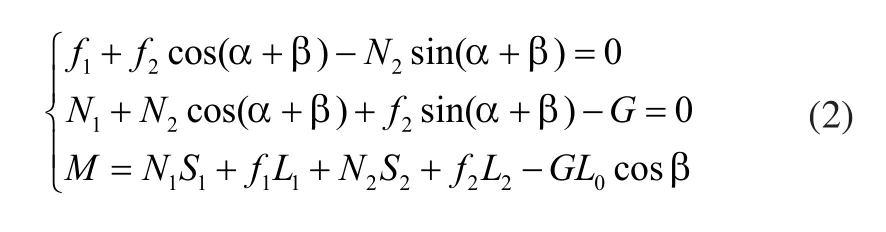
由式(1)、式(2)可以得出:

履带翻越障碍物阶段Ⅱ如图2(c)所示,平衡条件为:

可以得出:
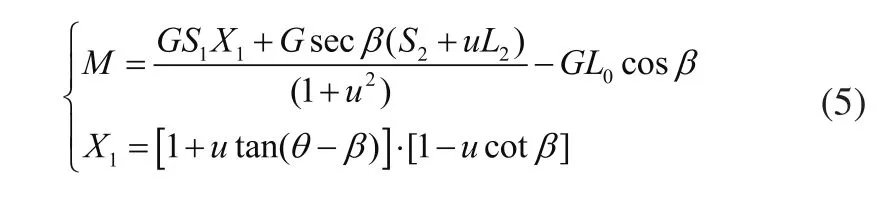
式中:G为履带机器人重力;N1为后支撑轮地面支撑力;N2为障碍物对履带支撑力;f1为地面对履带摩擦力;f2为障碍物对履带摩擦力;L为履带接地长度;L0为质心与主动轮转轴中心距离;L1、L2分别为地面支撑力和障碍物对履带支撑力与主动轮转轴中心的垂直距离;S1、S2分别为地面支撑力和障碍物对履带支撑力与主动轮转轴中心的水平距离;α为履带前角大小;β为履带与地面夹角;H为障碍物高度;θ为履带后角大小。
当履带机器人前角大小α设计一定时,履带上升过程中所需转矩M随β与S2和质心距离L0变化如图3所示。从图3可以看出,在越障过程中随着履带攀升,履带与地面夹角β随之变大,从而越障所需转矩M也随之增大。同时S2的减小也会使越障所需转矩M也随之减小。从式(3)、式(5)可以看出,当履带机器人后支撑点未脱离地面时,将履带机器人质心与主动轮转轴中心距离L0增大,越障所需转矩M也随之减小。但是当L0增大到一定程度,后支撑力N1作用时间变短,越障阶段2只有支撑力N2,短时间内所需上升力f2增大。根据Rf2=M可以得出当L0增大时会使越障阶段2所需转矩M增大。

图3 越障过程所需转矩的变化
当履带机器人质心绕过障碍物支撑点时,履带机器人由开始翻转,这时平衡条件为:
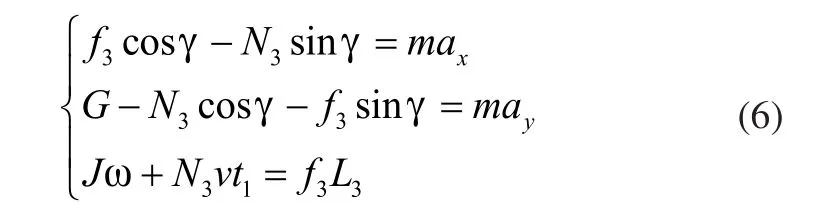
可以得出:

式中:N3为障碍物顶点对履带支撑力;f3为障碍物顶点对履带摩擦力;m为履带机器人质量;L'0为履带机器人质心到后负重轮距离,L3为履带机器人质心到履带接地处距离;γ为机器人翻越障碍物时履带地面夹角;ax、ay为履带机器人翻转时由重力对质心产生的x,y方向加速度;t1为履带机器人质心过障碍物顶点线后经过的时间,R为主动轮半径,ω为绕支撑点下落的角速度。
履带越障第三阶段时,当 L0增加,机器人质心越过障碍物法线的时间更快,会使同一t1时间内履带机器人绕支撑点的角速度ω值更大,从而增大越障第三阶段所需力矩[10]。
当履带机器人完全翻越过障碍物时,地面对履带机器人第一负重轮产生冲击,根据冲量定理和冲量矩定理有:
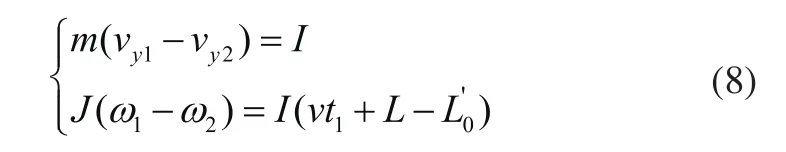
式中vy1为履带机器人越障后碰撞前速度;vy2为履带机器人越障后碰撞后速度;I为碰撞冲量,J为履带机器人转动惯量;ω1为碰撞前履带机器人绕障碍物支点的角速度,有ω1=;ω2为碰撞后履带机器人绕障碍物支点的角速度。
假设履带机器人越障后前负重轮碰撞点为A,碰撞前A点速度vA,碰撞后速度为v'A,设机器人与地面碰撞恢复因子为K[11],则:
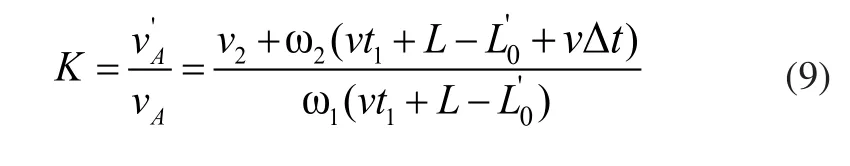
综合式(6)~式(9)得出履带机器人越障后与地面碰撞冲量I为:
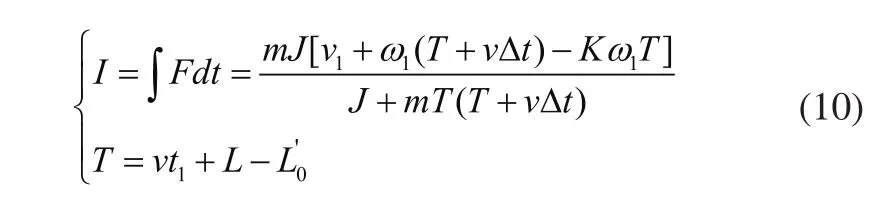
可以从式(7)、式(10)得出,当履带机器人质心的改变,会改变越障后地面给履带机器人带来的冲击。质心靠后会使翻越障碍物时间变长,增加已越过障碍物车身长度,增加翻转角速度从而增加负重轮冲击力;而质心过于靠前会使履带越障成功后使负重轮受到较大的负载响应。
3 仿真分析
3.1 模型、参数建立
为了更加可靠的分析机械臂姿态对履带机器人其越障的影响,在Recurdyn中建立履带模型,模型中包含一个虚拟履带机器人。通过改变机械臂姿态从而改变履带机器人的质心。由于工作中需要将机械臂末端关节与地面平行,仿真中改变机械臂两臂的夹角,夹角从0°增加到90°,间隔10°变化。
3.2 数据分析处理
3.2.1 同一姿态越障
当履带机器人以某一姿态越障时,其影响越障能力的因素为前角大小α、履带与地面夹角β。越障阶段1,当前角大小一定时,越障过程所需转矩随夹角β的增大而增大,仿真与理论一致。越障阶段2所需转矩受地面夹角β影响变化较小,如图4所示。

图4 同一姿态越障转矩变化
3.2.2 不同姿态越障阶段Ⅰ
通过仿真得出了同一速度下不同姿态的履带机器人越障阶段1的驱动转矩的变化,变化如图5所示,变化值如表1所示。可以看出当机械臂姿态改变而改变履带机器人质心位置使越障第一阶段所需转矩变化,当机械臂夹角增大使履带机器人质心向前偏移时,越障所需转矩逐渐减小,仿真与理论一致。而90°时转矩变化突然变大,是因为质心已经靠近前角附近,使履带机器人的机械臂均布压力分布在前角处。
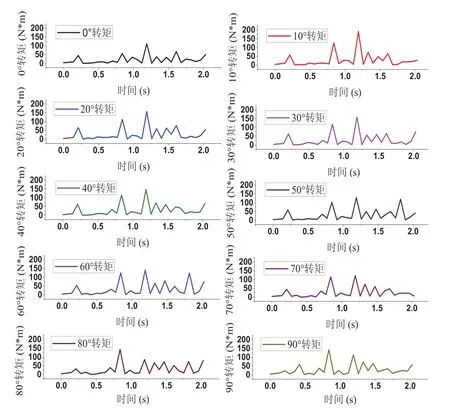
图5 各姿态越障转矩变化

表1 转矩变化值
3.2.3 不同姿态越障阶段Ⅱ
当履带机器人进入越障阶段2,由于影响因素地面夹角β对同一姿态的机器人越障影响较小,而机械臂的姿态对其影响较大,不同姿态越障阶段2所需平均转矩如图6所示。可以看出当机械臂改变姿态使质心向前位移时,越障阶段2所需扭矩增大,仿真与理论一致。

图6 转矩平均值
3.2.4 不同姿态越障对负重轮冲击
当履带机器人质心过障碍物法线时,由重力给机器人产生翻转力,使机器人成功越障。在越障阶段3中,由机器人姿态改变而引起的质心位置变化使越障后地面对负重轮产生的冲击力改变,质心过于靠前和靠后都会增加负重轮冲击力如图7所示。
4 样机实验
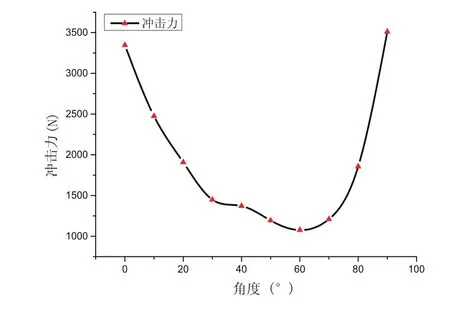
图7 越障后负重轮冲击力
在理论分析和虚拟仿真得到预期数据后,根据自行设计的双履带式移动机器人进行越障实验。机器人底盘高度为250mm,带有三自由度机械臂,越障高度为200mm。在进行反复多次实验后发现,机械臂以夹角为40°~60°之间进行越障时对越障过程Ⅰ中所需电机负载转矩较小;机械臂以0~40°之间进行越障对越障阶段Ⅱ所需电机负载转矩较小。以机械臂夹角为30~60°越障对在越障阶段Ⅲ的过程中较稳定,且越障完成后,履带落地冲击对负重轮影响较小。

图8 样机实验
5 结论
本文通过理论分析计算和运用三维绘图软件SolidWorks与多体动力学仿真软件Recurdy共同建立双履带机器人仿真模型。对越障过程的计算,获得了双履带机器人在越障过程中所需要的转矩和越障后地面对履带负重轮的冲击力。并通过改变机械臂姿态来优化越障过程中所需要的转矩和越障后地面对负重轮的冲击力,得到了较优的越障姿态。优化了履带机器人越障所需负载转矩和受到的冲击振动,为提高双履带机器人越障性能和提高机器人使用寿命提供了重要指导意义。
参考文献:
[1]朱岩,王明辉,李斌,王聪.履带可变形机器人越障性能研究[J].机器人,2015,37(6):693-701.
[2]王建,谈英姿,许映秋.基于姿态的多关节履带机器人越障控制[J].东南大学学报(自然科学版),2011,41(s1):160-167.
【】【】
[3]欧屹.特种地面移动机器人机械系统设计与分析[D].南京:南京理工大学,2013:12-110.
[4]王伟东.面向复杂地面环境的作业型履带式移动机器人研究[D].哈尔滨工业大学,2009:15-30.
[5]曹毅.冲击下履带车辆动载特性及综合传动结构分析研究[D].北京理工大学,2016: 15-37.
[6]Dwivedy S K,Eberhard P. Dynamic analysis of flexible manipulators, a literature review[J].Mechanism & Machine Theory,2006,41(7):749-777.
[7]王伟东,吴冬梅,董为,等.基于虚拟激励和精细积分的移动手臂非平稳随机激励下振动分析[J].振动与冲击,2013,32(20):72-75.
[8]饶伟,施家栋,王建中.关节式履带机器人爬楼梯动态稳定性分析[J].机械工程学报,2014,(15):60-67.
[9]张婧,张俊俊.一种特殊结构履带机器人设计及爬楼梯打滑性分析(英文)[J].机床与液压,2014,(06):91-96.
[10]韩广,王田苗,梁建宏,赵建昌.一种有效爬越楼梯的模块化可重组履带结构[J].机器人,2004,26(5):400-403.
[11]莫海军,朱文坚.履带式移动机器人越障稳定性分析[J].机械科学与技术,2007,(01):65-67.
[12]刘义.RecurDyn多体动力学仿真[M].北京:电子工业出版社,2013:1-564.
[13]王良曦,王红岩.汽车动力学[M].北京:国防工业出版社,2008:1-317.

