差速轮式移动机器人的导航算法研究及仿真实验

0 引言

轮式移动机器人主要有4种结构形式被广泛的熟知，即前轮驱动并可转向移动机器人、两轮差动驱动的移动机器人、汽车式移动机器人、带拖车的轮式移动机器人、三轮全向移动机器人[1]。移动机器人因具有多种机构形式，使得它的应用也渗入到各个领域，包括深海无人潜水器、无人飞行器、服务机器人和工业机器人等。移动机器人的广泛应用使得人们的生活和生产发生了很大的变化，提高了生产效率和生活质量。因此移动机器人的协调和协作、导航定位、路径规划、控制等问题的研究引起了广大科研工作者的关注。其中自主导航技术是其研究的核心[2,3]，而定位是完成导航首先要解决的问题[4]。

本文主要对轮式移动的差速底盘的机器人的定位导航问题展开研究，着重分析导航算法中直线导航和圆弧导航，针对这两种导航算法只是基于单一的角度变量进行纠偏的问题进行分析和改进，并提出新的改进算法，为移动机器人的更深入的研究奠定坚实的基础。

如图1所示为移动机器人路径规划导航定位结构图。

1 轮式机器人差速定位算法

1.1 差速轮式机器人的系统介绍

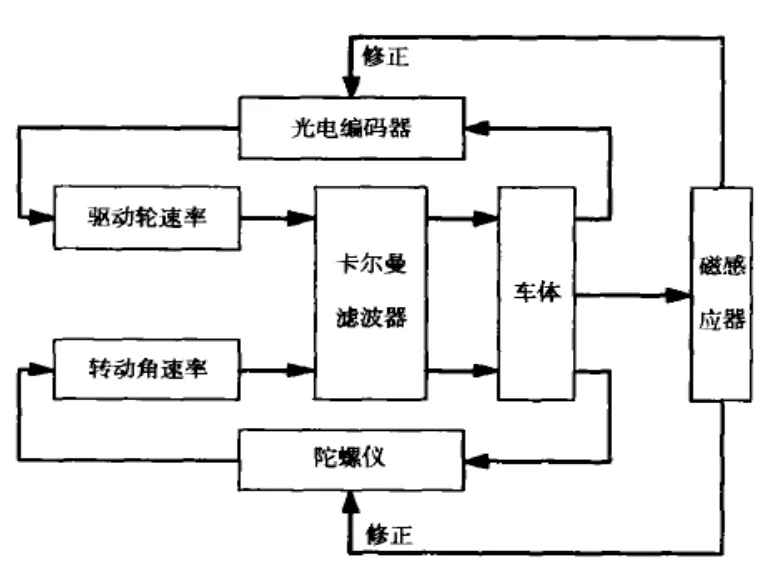
图1 移动机器人导航结构图

差速轮式移动机器人，主要依靠后边的驱动轮驱动前方的轮子进行控制，使机器人按照预定的轨迹行走。这种结构底盘的机器人灵活转向，依靠速率和方向的不同，实现直线行走和转弯的目的[5]。

本系统机器人采用光纤陀螺与光电码盘实现机器人的定位，使用光纤陀螺的信号可以读取相对于起始点的角度数据，这样就可以通过相对位置、角度信息解算得到机器人相对于起始坐标系的坐标信息，从而实现机器人的定位。

1.2 轮式机器人差速定位

如图2所示为系统定位的示意图，[xyθ]表示机器人的系统定位信息。

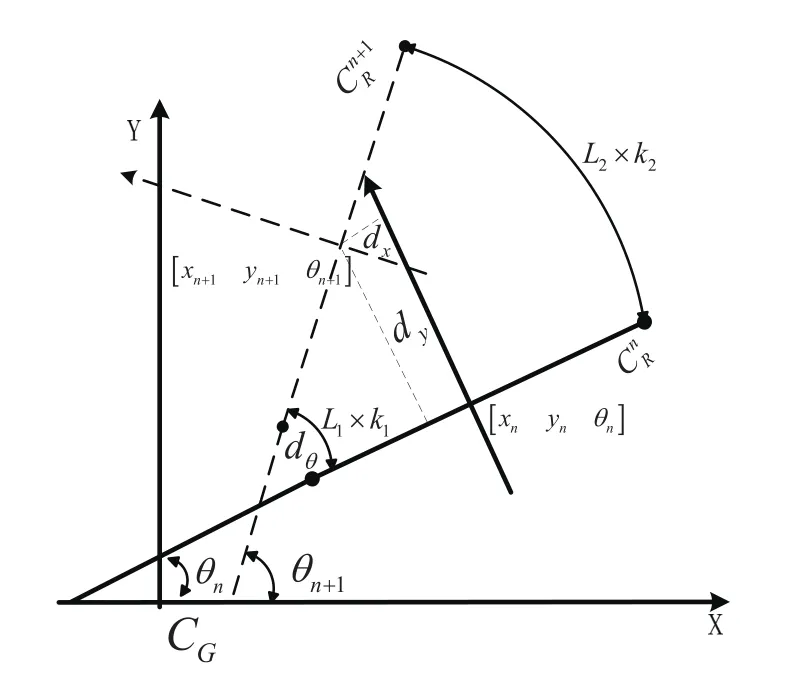
图2 系统定位示意图

图中：x,y为机器人全局坐标系下的坐标；θ为机器人的方位角；Cg，CR为全局、局部坐标系。

假设机器人由第m个状态到达第m+1个状态时，即经实线到达虚线时，产生很小的位移量。从图中可以看出从动轮会行走一段很短的圆弧。假定机器人左侧编码器的变化量为L1，右边的变化量为L2。N表示编码器的分辨率，r表示从动轮半径，Len为两边编码器从动轮的中心轮距[6]。则有以下公式：

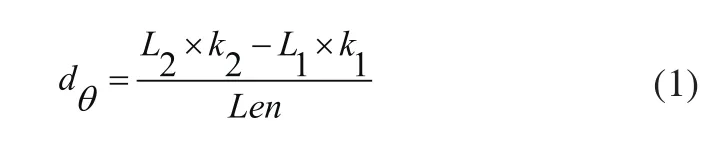
式中：dθ表示机器人旋转的角度，k1=2πr1/N和k2=2πr2/N表示两侧编码器的矫正系数，再由dθ值能够求出在CR中x,y方向的变化量：

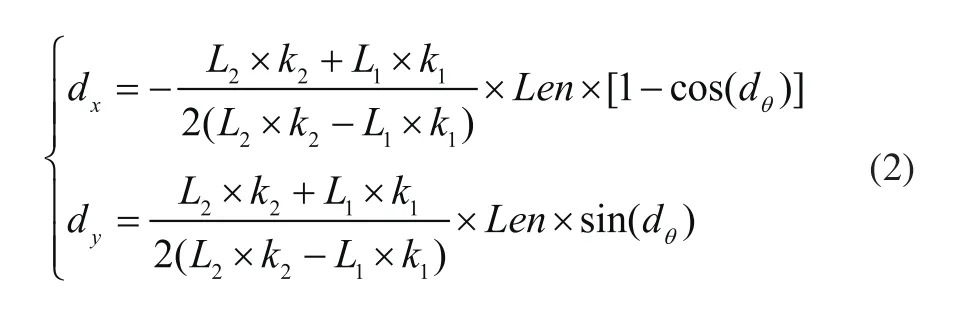
进行以下公式的变换，可以将dy，dx，dθ转换为在全局坐标系中的角度与位置信息：

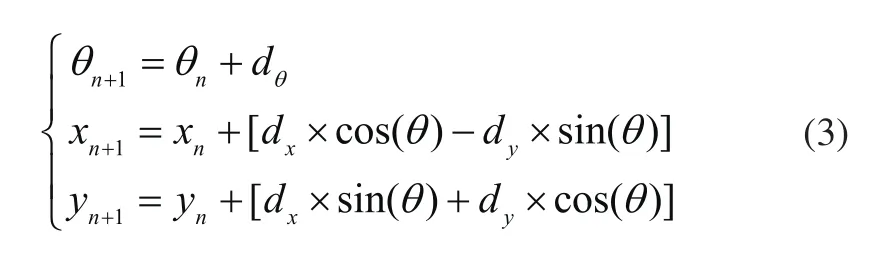
其中[xnynθn]表示前一时刻的定位信息，[xn+1yn+1θn+1]表示当前时刻的位置信息。得到的坐标信息和陀螺得到的坐标信息做数据融合后经过累加得到机器人的实时坐标信息。

由以上的运算可知，这个过程存在累积误差，经过长时间的作业之后，累计误差使机器人的定位信息出现偏差。以下使用累计误差修正算法对误差进行消除[7]。圆形的中心与从动轮中心的距离为l，圆的坐标为则机器人的当前的位置信息如下公式所示：

实验表明，通过以上的累计误差修正算法的机器人，在没有受到严重的破坏的条件下能够很好的实现系统的定位信息，文献[7]也通过具体的实例验证了这种累计误差修正法的有效性和正确性。

2 直线导航算法

将差速底盘机器人底盘的定位信息通过串口传送到以ARM和FPGA为控制核心的主机上，在主机上采用直线、圆弧导航算法实现机器人的导航。通过分析和对比，发现了这两种导航算法中存在的问题，以下分别对这俩种导航算法进行了改进。提高了机器人导航的精度。

2.1 直线导航算法

如图3所示为机器人直线导航算法的示意图，根据系统的位置与角度来实现机器人的反馈。利用目标点和编码器中心点的连线和当前机器人行走方向的夹角作为反馈参数，使用机器人与目标点的距离作为判断是否到达的条件[8]。

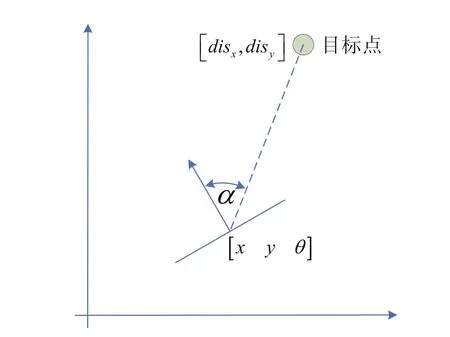
图3 直线导航算法示意图

如图3所示，机器人车头方向与目标点的夹角为α，目标点的坐标为[disx，disy]，利用下面的公式可以把目标点的坐标转化为机器人的局部坐标值：

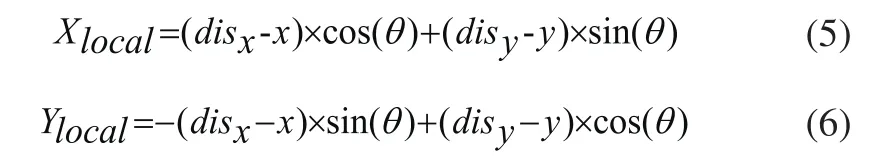
利用得到α值（当Xlocal＜0时取负号），由α的值使用PID反馈调节，通过下面的公式对车头方向进行调整。

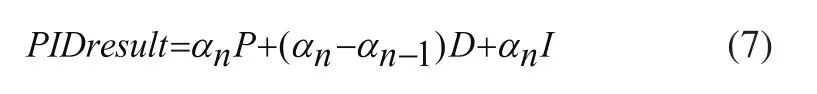
式中，PIDresult为调整量，αn与αn-1为当前时刻和上一时刻的α值。

2.2 改进的直线导航算法

上述的导航算法是针对角度单一变量进行纠偏，越接近终点时纠偏效果越剧烈，当PID参数很大时，会导致很大超调，因而该算法需要做一定改进，设计直线导航算法：

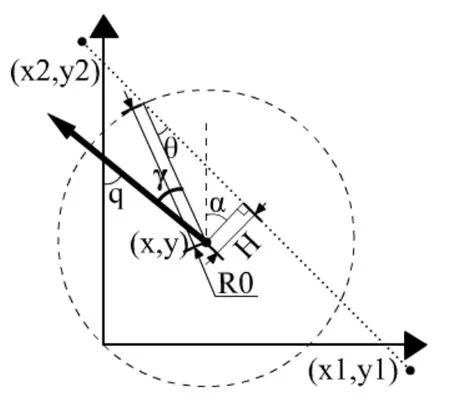
图4 改进的直线导航示意图

在平面坐标系中，机器人位置为（x，y）朝向角度为q。设定机器人半径为R0，目标直线为由点（x1，y1）和（x2，y2）确定。有以下关系：

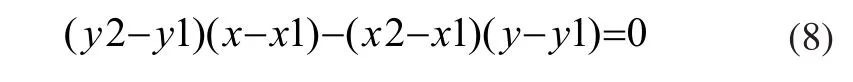
H为点到直线距离：

又有：

可以求出角度γ，然后对角度αn进行PID控制就行了。

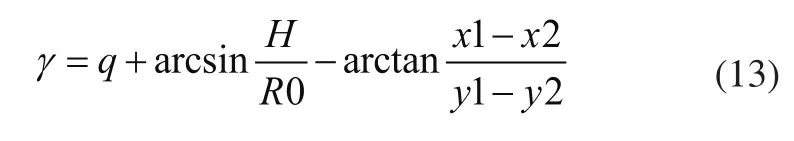
3 圆弧导航

圆弧的导航可以参照图3。只不过目标点改为了圆心，我们所要PID的角度变成了机器人现有角度与圆切线间的夹角。利用下面的公式可以把目标点的坐标转化为机器人的局部坐标：

之后使用来求出α值。

调整公式依然是：

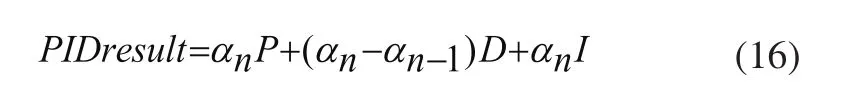
3.1 改进的圆弧导航算法

由于原有导航算法是针对角度单一量进行纠偏，越接目标时纠偏效果越剧烈，当PID参数很大时，会导致很大超调，因而该算法需要做一定改进，设计直线导航算法圆弧导航算法，设计算法图示如图5所示。

图5 圆弧导航示意图

首先将目标圆心进行坐标系转化，得到其在机器人的坐标系（机器人所在位置为原点，机器人运动方向为x轴方向）内的坐标（x0，y0）。以直线与目标圆交点处切线方向进行改进的直线导航即可。有：

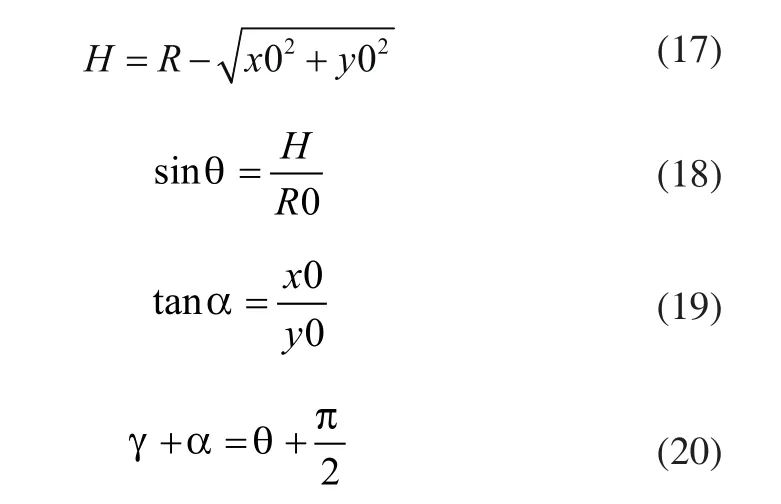
可以求出角度γ：

对角度γ进行PID之后，对于轨迹是直线和圆弧相切时，导航的目标点也是一个连续变化的点，不会出现导航的突变，机器人的运动会更平滑精确。

3.2 驱动轮速分配

基于对多种情况的考虑，可以将速度分配写成一个通式，V,V1,V2表示机器人实时的平均、右轮、左轮速度。

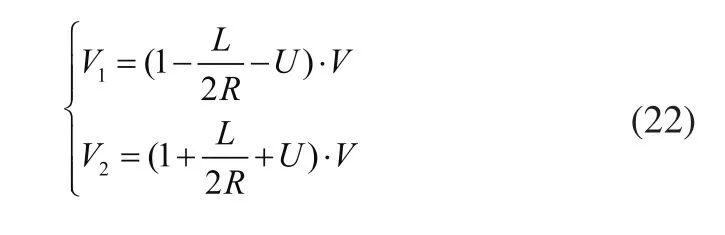
式中：R为圆弧半径（向量），规定圆心在路径右侧为正，左侧为负；L为驱动轮间的距离；U为由偏差产生的控制量；

将U定义为向量，基于不同的情况进行考虑，总结控制量与偏差量符号变化情况，将其归纳为一个统一公式。

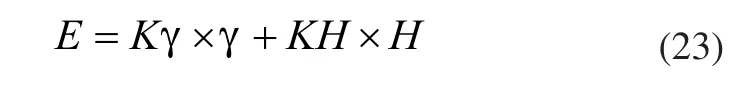
之后再将偏差E经过PID控制，然后使用控制量U分配左右轮的速度从而达到纠偏的用途。

4 Simulink仿真验证

针对以上提出的改进算法，对圆弧导航算法的改进前后进行仿真验证，仿真数学模型如式(24)所示：

上述模型能够表示出机器人在行进时轮速与偏差量随时间变化的关系，H,为距离与角度偏差初值；H,,V1,V2,V,KH,K如上述介绍；为了让仿真变得简单，设定KH的值，只让K的值发生改变，如图6所示的就是仿真得到的改进前后的圆弧导航算法的路径。

图中实线为改进后的圆弧导航算法的路径，虚线改进前的圆弧导航算法的路径，横纵坐标轴的都是以mm计量的。由图6知，改进前与改进后在初始时基本没有差异，但是在最后只有大约15mm的误差。从导航数据可以分析出，此偏差主要是由陀螺引起的。由陀螺传送的与真实角度存在一个误差Δα，机器人就会纠偏，Δα主要有以下的两点产生：

1）由于本文使用的是单轴陀螺，即使旋转一圈是2π，Δα会出现从0逐步增大，再逐不减小到0的过程。

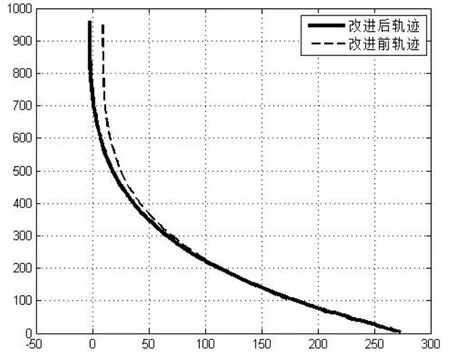
图6 改进前与改进后结果对比图

2）理想中的陀螺的精度可以满足实际的情况，但是现实这一定会有误差。

5 结论

轮式的差速底盘移动机器人的导航算法中的直线和圆弧导航只是针对单一角度变量进行纠偏，且越接近终点时纠偏效果越剧烈，当PID参数很大时，会导致超调很大，因此对该算法进行了改进，提出了新的导航算法。最后建立Simulink模型进行仿真。仿真结果表明新的导航方法取得了良好的效果。

参考文献：

[1]沈猛.轮式移动机器人导航控制与路径规划研究[D].陕西:西北工业大学,2006:3-4.

[2]Bashiri M,Vatankhah H, Ghidary S. Hybrid adaptive Differential Evolution for Mobile Robot Localization[J].Intelligent Service Robotics.2012,5(2):99-107.

[3]Cheng P Y,Chen P J.Navigation of mobile robot by using D+algorithm[J].Intelligent Service Robotics.2012,5(2):229-243.

[4]贝旭颖,平雪良,高文研.轮式移动机器人里程计系统误差校核[J].计算机应用与研究,2017,35(9).

[5]亢海龙,徐娅萍,王涛,等.基于卡尔曼滤波器的轮式机器人定位方法[J].机械与电子,2009,72-74.

[6]王鸣.机器人实时定位与导航系统仿真设计研究[J].计算机仿真,2012,12(03):216-218.

[7]李毅,吴焱岷,宏英.机器人实时定位与导航系统的设计研究[J].制造业自动化2012,34(4):132-134.

[8]朱磊磊,陈军.轮式移动机器人研究综述[J].机床与液压,2009,37(8):242-247.