一种有效解决离轴数字全息相图倾斜畸变的数字参考平面方法∗

李芳 王明清 郑明 卢苇 于庆南 贾燕 吴坚

(北京航空航天大学物理科学与核能工程学院,北京 100191)

1 引 言

离轴数字全息由于参考光的倾斜入射可以使零级衍射、重建像及共轭像在波场的重建过程中彼此分离,从而方便地在成像中消除零级衍射和共轭像的影响而获得广泛的应用[1,2].其中,平面光波由于计算简单,是离轴数字全息中广泛使用的一种参考光波形[3−5].然而,这种离轴成像方式由于引入了参考波的附加载波频率会导致重建像产生倾斜相位畸变[6].针对此问题最直接的解决方案就是设法测得平面参考波的附加载波频率或倾角,然后将其代入重建算法而消除倾斜畸变.这种方法的核心问题在于如何准确地测得平面参考光波的附加载波频率或倾角值.因为到目前为止,通过实验方法很难准确地测出参考光波的附加载波频率值或倾角.

为解决这个问题,国内外的研究者提出了多种解决方案,大致可以分为双曝光法[7]、数字参考波法[8−13]、频谱中心法[14−16]及自动修正算法[17−21].其中,双曝光法通过分别记录包含物体和不含物体的两幅双光束干涉全息图并进行相减以对重建相图的倾斜畸变做出修正.由于该方法需要记录两幅全息图和要求系统具有高稳定性,因此难以用于动态成像.而数字参考波法是通过建立和开展数字参考波的计算以确定其载波频率,从而达到对重建相图的倾斜畸变修正的目的.该方法需要一些特殊的条件,例如在全息图平面的物波场需为缓变场、针对微小物体或平坦物体成像.除此以外,像素大小对条纹分辨率的影响也限制了获取参考波载波频率的精确性,因此该方法具有一定的局限性.频谱中心法是将全息图变换到频域,通过寻找和定位物体频谱的最大值点并移动到坐标中心而消除重建相图倾斜畸变的方法.这种方法易受像素分辨率及噪声的影响而难以准确定位物体频谱的最大值,因此重建像仍会存在一定的残留畸变.自动修正算法通过在波场的重建计算中引入相位掩模来修正相位畸变.该方法更多地用于透镜导致的二次相位畸变的修正,是一种理论上的理想模型,如果存在噪声和环境扰动的影响,则会出现较大误差.

为了找到能更好地解决离轴数字全息成像中相图倾斜畸变修正问题的方法,本文提出了一种基于无透镜离轴数字全息成像的倾斜相位畸变修正的数字参考平面算法.对该方法的论述包括:1)相图的解包裹重建和抑噪处理;2)从相图选点以构建一个能准确反映相图倾斜的数字参考平面;3)建立数字参考平面参量与平面参考波载波频率的数学关系;4)以构建的数字参考平面为判据进行倾斜相位畸变修正的迭代计算;5)实验验证.

2 算法原理

2.1 理论模型

离轴数字全息成像中,物平面、全息图平面以及像平面的坐标关系如图1所示.

图1 离轴数字全息成像中的物平面、全息图平面以及像平面的坐标关系Fig.1.Coordinate systems of object,hologram and reconstructed image planes for digital o ff-axis holography.

物光波和参考光波在全息图平面干涉产生的全息图强度可表达为

其中,和分别表示物光波和参考光波的复振幅;||2+||2表示零级衍射强度;分别表示再现像及其共轭像强度.对于无透镜离轴数字全息系统,在全息图平面(z=0)处的平面参考光波复振幅(x,y)可以表示为

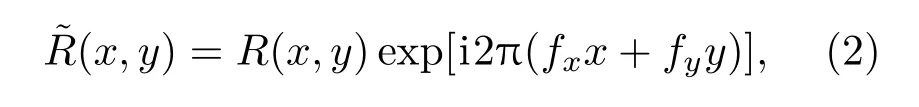
其中,R(x,y)是参考光波的实振幅,(fx,fy)是平面参考光波分别在x和y方向上的实际载波频率.

通过对参考光波倾角的适当设计可以方便地使(1)式中的三项在成像平面彼此完全分离,如此零级衍射和共轭像可以通过简单的频域滤波消除.因此,将(2)式代入(1)式并去除零级斑和共轭项,则滤波后的全息图强度可表示为

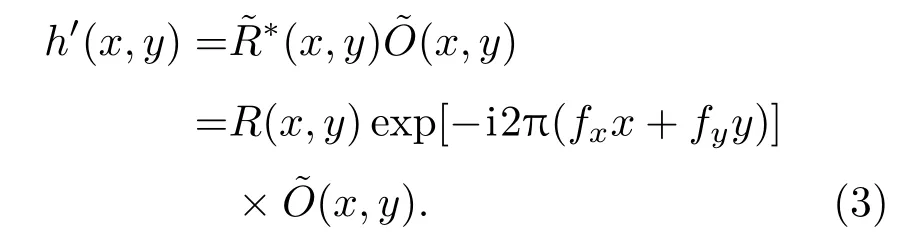
依据傅里叶光学和基尔霍夫衍射理论,在像平面重建的物波场可以写为

式中,i/λ是系数;λ是光波长;r是全息图平面和像平面上任意两点间的距离;是用于图像重建计算的参考波复振幅,其表达式为

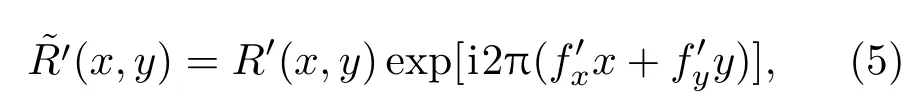
其中R′(x,y)是实振幅,是参考波分别在x′和y′方向上的名义载波频率值,它等于平面参考光波载波频率的设计值.由于实际记录全息图的平面参考光波的载波频率难以准确测知,因此用于图像重建的参考波的名义载波频率并不严格地等于参考光波的实际载波频率(fx,fy),即设计值不等于实际值.因此,两个参考波的载波频率与(fx,fy)会存在一定的频差,这个差值将导致重建相图的倾斜畸变.将(3)和(5)式代入(4)式得到重建像的光场为

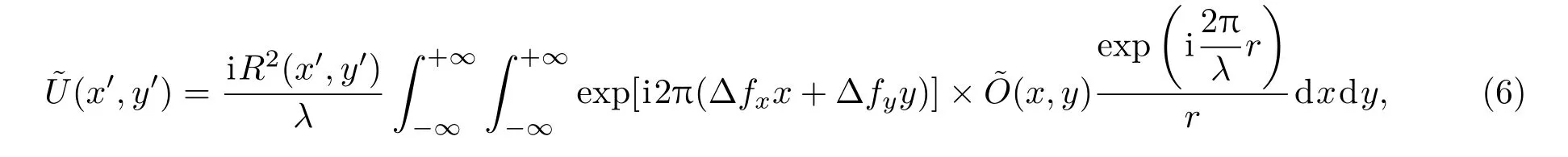
其中,根据傅里叶光学理论,由于积分中第一项的相位因子2π(∆fxx+∆fyy)是线性相因子,因此重建的图像会发生一定的偏转而偏离图像平面中心,即导致图像的倾斜相位畸变.根据(6)式,显然如果∆fx和∆fy等于零,则重建的图像会准确地呈现在平面中心而没有倾斜畸变.由于在数字全息中用于图像重建的参考波是以数字波函数的形式体现,因此可以通过修正该参考波的名义载波频率值使(∆fx,∆fy)=0,即达到与全息图记录使用的参考光波实际载波频率一致.

为实现这个目标,我们构建了一种能够准确反映图像重建中倾斜相位畸变程度的数字参考平面.具体方法是首先获得三维重建相图并做抑噪处理以减小修正误差.然后在相图的平坦区域内随机选取三个点的空间坐标值以建立数字参考平面方程:

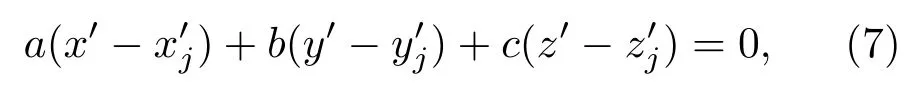
其中,(a,b,c)是反映数字参考平面倾斜程度的系数,它对应于重建图像的倾斜.数字参考平面的法向量指示了倾斜的方向和大小,可以表示为

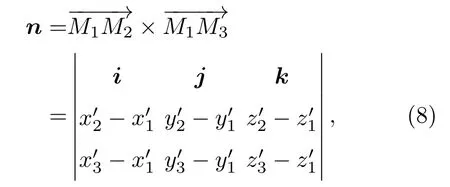
其中,(i,j,k)对应于(x′,y′,z′)方向的单位向量;系数(a,b,c)的值可以通过计算n的行列式来获得.由于(6)式中的线性相因子引起的图像偏转倾斜和(7)式中差分系数(a,b)表示的图像平面倾斜指示的是同样的结果,因此以下的对应关系能够被建立:

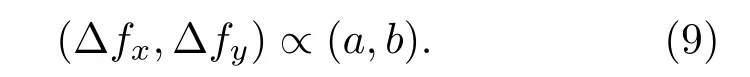
以上关系显示,如果系数(a,b)的值等于零,则显然(∆fx,∆fy)也等于零,即图像重建的数字平面参考波的名义载波频率将等于全息图记录的实际平面参考光波的载波频率值(fx,fy).在这种情况下,实际平面参考光波的载波频率值(fx,fy)也得以准确地确定.基于这种考虑,在随后对名义载波频率值的修正计算中,将数字参考平面参量(a,b)值的变化设为判定∆fx和∆fy是否为零的判据.修正名义载波频率值和倾斜相位畸变的迭代计算过程如图2所示.

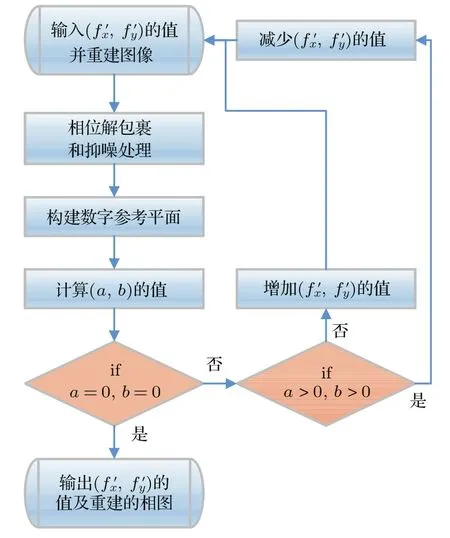
图2 修正数字参考波名义载波频率和倾斜相位畸变的迭代计算流程Fig.2.Flow-chart for correcting nominal carrier frequencies,of the numerical reference wave and tilt phase distortion.

2.2 模拟分析和验证

对该方法的计算机模拟实验结果如图3所示,图3(a)是原始物体.模拟实验中,引入高斯噪声作为对激光散斑噪声的模拟[22].假设用于全息图记录的斜入射平面参考光波的载波频率设计值为实际值为fx=890 cm−1,fy=890 cm−1.因此,用于全息图重建的数字参考波的名义载波频率值为与参考光波的实际载波频率不等.利用菲涅耳重建算法[23]和PUMA相位解包裹技术[24]获得的重建相图如图3(b)所示,其结果不仅显示了明显的相位倾斜畸变,而且还有噪声引起的相位畸变.因此,为了有效地修正相图的倾斜畸变,在使用平稳的PUMA解包裹算法的基础上,做了进一步的抑噪处理.首先通过双边滤波[25]以有效保留去噪后的图像高对比度边缘特征信息,然后进一步通过包含小波收缩的短时傅里叶变换以更好地保留图像纹理特征等低对比度信息[26].抑噪处理的基本原理可以在数学上表示为

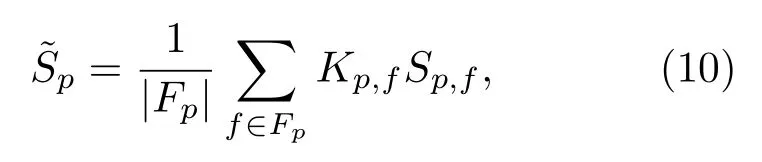
其中,Sp,f是噪声傅里叶系数;Fp是所有小波收缩信号的平均值;Kp,f是与噪声标准差σn有关的收缩系数;p表示噪声被抑制后的结果.然而,由于残余噪声的不确定性,很难确定已解包裹相位的噪声标准差σn.对此,我们使用噪声标准差的评估公式,该值表示为

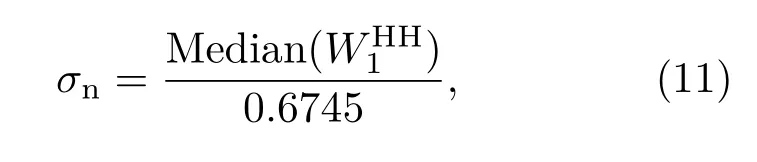
其中,是高频子频带的正交小波转换系数,Median表示在计算中的中值,0.6745是基于经验公式获得的参数[27].经上述抑噪处理的结果如图3(c)所示.解包裹后的重建相图中的噪声得到有效抑制,为随后的数字参考平面构建和倾斜畸变的修正提供了保障.

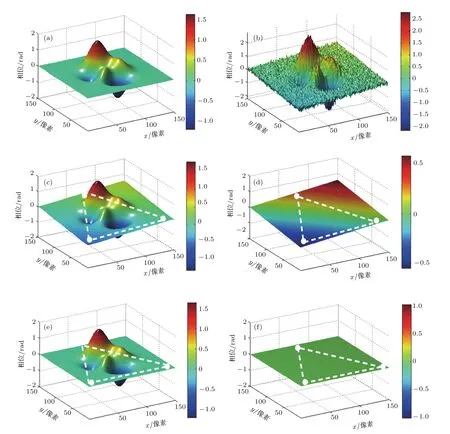
图3 仿真计算结果 (a)原始物体;(b)包含噪声的PUMA解包裹相图;(c)抑噪处理后的相图;(d)构建的数字参考平面;(e)倾斜相位畸变修正后的相图;(f)倾斜相位畸变的误差分析Fig.3.Simulation results:(a)Original object;(b)reconstructed phase map with noise using PUMA phase unwrapping technique;(c)phase map with noise removed;(d)constructed numerical reference plane;(e)phase map with tilt phase distortion corrected;(f)error analysis of the tilt phase distortion correction.

根据上述的数字参考平面构建原理,在图3(c)的平坦区域选择三个点的坐标,利用(7)式建立数字平面方程,获得反映图像倾斜程度的数字参考平面,如图3(d)所示.显然,在这种情况下(a,b)值不等于零.然后,利用图2的流程,对参考波的名义载波频率进行修正的迭代计算,计算的误差值控制在|a|<10−5和|b|<10−5.当频率值为时,倾斜相位畸变修正的结果如图3(e)所示.修正的误差如图3(f)所示.此时,(a,b)值为 (−5.4976×10−6,−5.8756×10−6).重建的相图(如图3(b)或图3(c))的倾斜畸变得到了很好的修正.同时,由(9)式和(a,b)值可知,(∆fx,∆fy)足够小,因此获得平面参考光波的实际载波频率为

作为比较,图4和表1给出了采用双曝光法[7]、数字参考波法[13]、频谱中心法[15]和线性拟合法[18]获得的相图倾斜畸变修正的仿真计算结果.图4(a)的双曝光法结果显示,相图的倾斜畸变能够得到很好的修正,但这仅仅是一种理想情况.由于该方法需要记录两幅全息图,因此不能有任何扰动的影响,也就很难在实际环境中获得理想结果.图4(b)是使用数字参考波法得到的计算结果,由于该算法仅在振幅域对图像进行处理,因此在相位域上仍会存在一定的误差和残余畸变,即相图的倾斜畸变未能完全修正.而图4(c)显示的频谱中心法计算结果是通过选取频谱最大值点并将其移至频谱中心实现相图畸变修正.该方法在像素分辨率及噪声的影响下,仅能定位物频谱的最大值点,参考波倾角或载波频率很小时,重建的相图仍会存在一些残留畸变而不能完全修平.图4(d)显示了采用线性拟合法获得的相图倾斜畸变修正结果.显然该方法的结果优于数字参考波法和频谱中心法的结果.由于线性拟合法是从相图中做直线拟合,即使取(x,y)双方向做直线拟合,仍然存在所取的直线区域过于狭小而难以准确表征整个二维平面,因此重建相图在使用该方法后仍然存在少量的残余畸变.

图4 不同方法的仿真结果对比 (a)双曝光法;(b)数字参考波法;(c)频谱中心法;(d)线性拟合法Fig.4.Comparison of the simulation results from different methods:(a)Double exposure technique;(b)numerical reference wave technique;(c)spectrum-centering algorithm;(d)linearly fitting method.

表1列出了图3和图4结果的量化对比分析.由于a和b是表征图像倾斜畸变修正程度的关键特征参量,因此对图4中不同方法得到的图像倾斜畸变修正结果,通过(7)式建立对应的平面方程可求得其(a,b)值.结果显示,本文提出的方法在修正相图倾斜畸变上更加精确.同时,基于图4的几种方法获得的实际平面参考光波的载波频率值与已知的890 cm−1比较也存在一定的误差.其中,双曝光法无法通过图像倾斜畸变的修正结果推算出实际平面参考光波的载波频率.

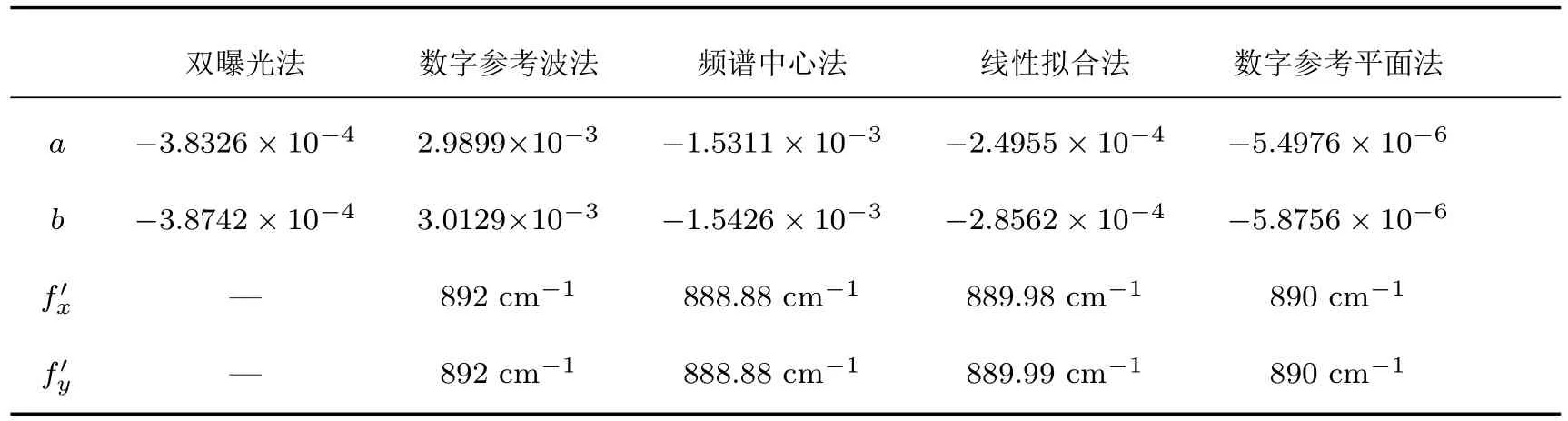
表1 不同方法的图像倾斜畸变修正结果Table 1.Results of image tilt distortion correction with different methods.

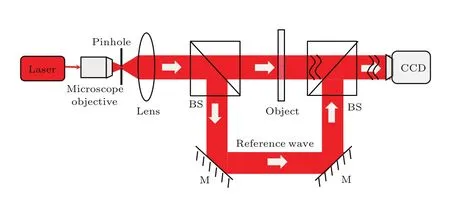
图5 离轴数字全息的实验光路图Fig.5.Experimental setup for digital o ff-axis holography.

图6 实验结果 (a)重建的分辨率板局部振幅像;(b)解包裹和去噪后的局部分辨率板相图;(c)构建的数字参考平面;(d)倾斜畸变修正后的分辨率板相图Fig.6.Experimental results:(a)Reconstructed amplitude image of a partial resolution plate;(b)unwrapped and de-noised phase map of the partial resolution plate;(c)constructed numerical reference plane;(d)phase map of the resolution plate with the tilt phase distortion corrected.

3 实验测量和验证

离轴数字全息实验光路如图5所示.其中,波长λ=632.8 nm的激光束经扩束系统和分束镜形成物光束和参考光束;被测物为三维分辨率板;用于记录全息图的电荷耦合器(CCD)传感器像素数1280×1024,像素尺寸5.2µm×5.2µm.倾斜的平面参考光名义载波频率设置为

实验结果如图6所示.其中图6(a)是利用菲涅耳算法重建的分辨率板局部振幅像,其结果包含了散斑等噪声信息;图6(b)是通过PUMA解包裹算法结合双边滤波及小波收缩短时傅里叶变换处理后得到的物体相图.显然,在重建物体三维图像的同时,实验中的噪声得到了有效的消除.但由于参考光的倾斜入射引入了附加的载波频率,重建相图出现一定的倾斜畸变.在相图的平坦部分取三点构建表征图像倾斜程度的数字参考平面,如图6(c)所示.此时,(a,b)值明显不等于零.利用图2的方法对数字参考波的名义载波频率进行修正迭代计算,实验单次迭代计算时间为7.8 s,迭代计算步长d的初始值为10,为提高计算精度,设置步长d=0.1×d.当计算的载波频率值为时,获得(a,b)=(2.43946×10−6,−7.43256×10−6),计算完成.其中,迭代计算33次,用时258 s.此时,图6(b)的倾斜相图得到了非常好的修正,如图6(d)所示.因此,获得的实际参考光波的载波频率值为fx=−291.47 cm−1,fy=−137.43 cm−1.误差在10−6量级.

4 结 论

在离轴数字全息中,使用倾斜的平面参考波以消除成像中的零级衍射和共轭像是一种简捷和广泛使用的方法,但由于倾斜平面参考波引入了附加的载波频率并很难通过实验测量准确地获得倾斜参考波的附加载波频率值,因此会导致重建的物体相图存在一定的倾斜畸变而无法完全修正的问题.对此本文提出了一种数字参考平面算法用以解决这一问题.该算法利用重建相图的平坦区域选点构建一个能准确表征相图倾斜的数字参考平面,并建立该平面参量与参考波附加载波频率的数学关系和作为随后相图畸变修正计算的判据.同时,所提出的方法不仅使用了平稳的PUMA相位解包裹重建算法,而且结合了双边滤波及小波收缩短时傅里叶变换的抑噪处理,最大限度地在消除噪声对修正倾斜相位畸变影响的同时获得较好的图像分辨率.因此该方法在环境和系统噪声的影响下仍然有效,不仅能很好地实现对倾斜相位畸变的准确修正,而且能准确地获得倾斜平面参考波的附加载波频率.模拟分析和实验结果均证明了该方法的有效性.对离轴数字全息获得准确的重建图像具有重要意义.

参考文献

[1]Wang H Y,Liu F F,Song X F,Liao W,Zhao B Q,Yu M J,Liu Z Q 2013Acta Phys.Sin.62 024207(in Chinese)[王华英,刘飞飞,宋修法,廖薇,赵宝群,于梦杰,刘佐强2013物理学报62 024207]

[2]Gu T T,Huang S J,Yan C,Miao Z,Chang Z,Wang T Y 2015Acta Phys.Sin.64 064204(in Chinese)[谷婷婷,黄素娟,闫成,缪庄,常征,王廷云 2015物理学报 64 064204]

[3]Wu Y C,Wu X C,Yao L C,Xue Z L,Wu C Y,Zhou H,Cen K 2017Fuel195 12

[4]Yuan C J,Zhong L Y,Wang Y P,Xu L X,Qian X F 2004Laser Technol.28 482

[5]Rong L,Xiao W,Pan F,Liu S,Li R 2010Chin.Opt.Lett.8 653

[6]Cuche E,Marquet P,Dahlgren P,Depeursinge C 2000Interferometry in Speckle Light(Berlin: Springer-Verlag)pp213–218

[7]Ferraro P,de Nicola S,Finizio A,Coppola G,Grilli S,Magro C,Pierattini G 2003Appl.Opt.42 1938

[8]Liebling M,Blu T,Unser M 2004J.Opt.Soc.Am.A21 367

[9]Colomb T,Cuche E,Charrière F,Kühn J,Aspert N,Frédéric M,Pierre M,Christian D 2006Appl.Opt.45 851

[10]Miccio L,Al fieri D,Grilli S,Ferraro P 2007Appl.Phys.Lett.90 041104

[11]Cui H K,Wang D Y,Wang Y X,Liu C G,Zhao J,Li Y 2011Acta Phys.Sin.60 044201(in Chinese)[崔华坤,王大勇,王云新,刘长庚,赵洁,李艳2011物理学报60 044201]

[12]Belashov A V,Petrov N V,Semenova I V,Vasyutinskii O S 2014J.Phys.C536 012003

[13]Pang T 2015J.Mod.Opt.62 816

[14]Cuche E,Marquet P,Depeursinge C 2000Appl.Opt.39 4070

[15]Cui H,Wang D,Wang Y,Zhao J,Zhang Y 2011Opt.Commun.284 4152

[16]Liu Y,Wang Z,Li J,Gao J,Huang J 2016Opt.Laser Eng.86 115

[17]Nguyen T,Bui V,Lam V,Raub C B,Chang L C,Nehmetallah G 2017Opt.Express25 15043

[18]Kim D C,Cho H J,Shin S,Jung W,Yu Y H 2009J.Opt.Soc.Korea13 451

[19]Wang H Y,Liu F F,Song X F,Liao W,Yu M J,Liu Z Q 2013Chin.J.Lasers40 196(in Chinese)[王华英,刘飞飞,宋修法,廖微,于梦杰,刘佐强 2013中国激光 40 196]

[20]Liu S,Xiao W,Pan F 2014Opt.Laser Technol.57 169

[21]Zhang D,Fan J,Zhao H,Lu X,Liu S,Zhong L 2014Optik125 5148

[22]Wang D Y,Wang Y X,Guo S,Rong L,Zhang Y Z 2014Acta Phys.Sin.63 154205(in Chinese)[王大勇,王云新,郭莎,戎路,张亦卓2014物理学报63 154205]

[23]Schnars U,Falldorf C,Watson J,Jüptner W 2015Digital Holography and Wavefront Sensing(Berlin:Heidelberg)pp39–68

[24]Bioucas-Dias J M,Valadao G 2007IEEE Trans.Image Process.16 698

[25]Durand F,Dorsey J 2002Acm.T.Graphic21 257

[26]Allen J B 1977IEEE.T.Acoust.Speech.25 235

[27]Donoho D L,Johnstone J M 1994Biometrika81 425