填充墙竖向不规则布置对框架结构抗震性能的影响

刘资玉

(合肥工业大学土木与水利工程学院,合肥 230009)

0 引 言

传统设计中,填充墙作为框架结构的非受力构件,一般只用作分隔空间和围护,不承担水平荷载的作用。但历次震害研究[1]表明,填充墙与框架梁柱协同工作、共同抵抗地震作用。填充墙为结构提供了较大的侧向刚度,在地震作用下能够承担一定的水平剪力,从这个角度来说,填充墙对于抗震是有利的。但是,不合理的布置填充墙会导致结构在竖向刚度分布不均匀,受力不合理,由此导致结构的薄弱层破坏也会给人民财产带来巨大的损失[2],如图1所示。

现行规范仅考虑填充墙刚度的贡献,采取乘以0.6～0.7的周期折减系数[3]的粗略方法,而对于填充墙的布置形式没能充分考虑,填充墙的竖向不规则布置会导致结构刚度在竖向不连续,可能导致结构薄弱层的产生,在地震作用下将会发生严重的破坏。本文将基于填充墙的宏观力学模型,对三种填充墙竖向不规则布置的框架进行整体建模,分析填充墙竖向不规则布置对于框架结构抗震性能的影响,并对地震响应最大的模型的竖向不规则布置提出改进方案。

图1 薄弱层震害Fig.1 Seismic damage of the weak layer

1 等效斜撑的计算

1956年,Polyakov首次提出单个等效斜撑模型的概念[4]。根据刚度等效的原则,将填充墙看作一根与墙同厚、具有一定有效宽度的斜杆,该斜杆只承受压力,与框架梁柱平面铰接,共同抵抗侧向力,而填充墙的自重则以竖向均布荷载的形式施加在梁间。该等效模型最核心的部分就是计算等效斜杆的有效宽度。本文采用Hashemi 和他的导师 Mosalam根据FEMA356修正的计算公式[5],等效斜杆单元有效宽度w,计算公式如式(1)、式(2)所示。

w=0.175 (λhcol)-0.4r

(1)

λ= [(Emtsin2θ)/(4EfeIhinf)]0.25

(2)

式中：hcol为框架柱的高度;r为填充墙的对角线长度;Em为砌体填充墙的弹性模量;t为填充墙的厚度;θ为填充墙对角线与水平方向的夹角;Efe为框架柱的弹性模量;I为框架柱的惯性矩;hinf为填充墙的高度。

2 工程概况

以一栋6层带填充墙钢筋混凝土框架结构为例,层高为3.6 m,各层柱截面尺寸为500 mm×500 mm,主梁截面尺寸为250 mm×500 mm,次梁截面尺寸为200 mm×400 mm,柱混凝土强度采用C30,梁、板混凝土强度取C25,钢筋均选用HRB400钢筋。填充墙采用蒸压粉煤灰加气混凝土砌块,厚度为200 mm,重度为5.5 kN/m3,砌筑砂浆强度等级为M5.0,线膨胀系数为8×10-6,泊松比取0.2,填充墙受压本构根据文献[6]提出的本构模型确定。抗震设防烈度7度,场地类别为Ⅱ类,设计地震分组第一组。轴网布置如图2所示。

图2 轴网布置图(单位:mm)Fig.2 Plan of axis net (Unit:mm)

3 有限元建模

本文采用SAP2000建立了4个模型,图3(a)为纯框架结构,仅考虑填充墙的重量;图3(b)为底部两层不布置填充墙,上面四层满布;图3(c)为中间两层不布置填充墙,其他四层满布;图3(d)为顶部两层不布置填充墙,下部四层满布。通过纯框架模型与带填充墙框架模型的对比来分析填充墙竖向布置不规则对结构抗震的影响。

图3 有限元分析模型Fig.3 Finite element models

3.1 模态分析

对4个模型进行模态分析,选取结构前三阶振型的分析结果如表1所示。纯框架模型周期最长,布置填充墙后,从模型二到模型四,随着填充墙的布置位置逐渐下移,结构自振周期逐渐减小,说明填充墙的加入增大了结构的侧向刚度,且随着墙体布置的下移,结构的刚度还有所增大。模型四在第二振型下主要表现为扭转属性,相比其他三个模型,前两阶振型主要为X向和Y向的平动。

表1 结构前三阶振型自振周期和质量参与系数Table 1 Period and quality participation factor of first three vibration modes

3.2 多遇地震下的反应谱分析

反应谱分析从根本上来说是一种拟动力分析方法,它使用动力方法得到质点地震响应,统计形成反应谱曲线,再用静力方法对结构进行分析。反应谱分析得到的结构响应信息可以很方便地在设计中应用[7]。图4为在反应谱工况下得到的各模型楼层最大水平位移。

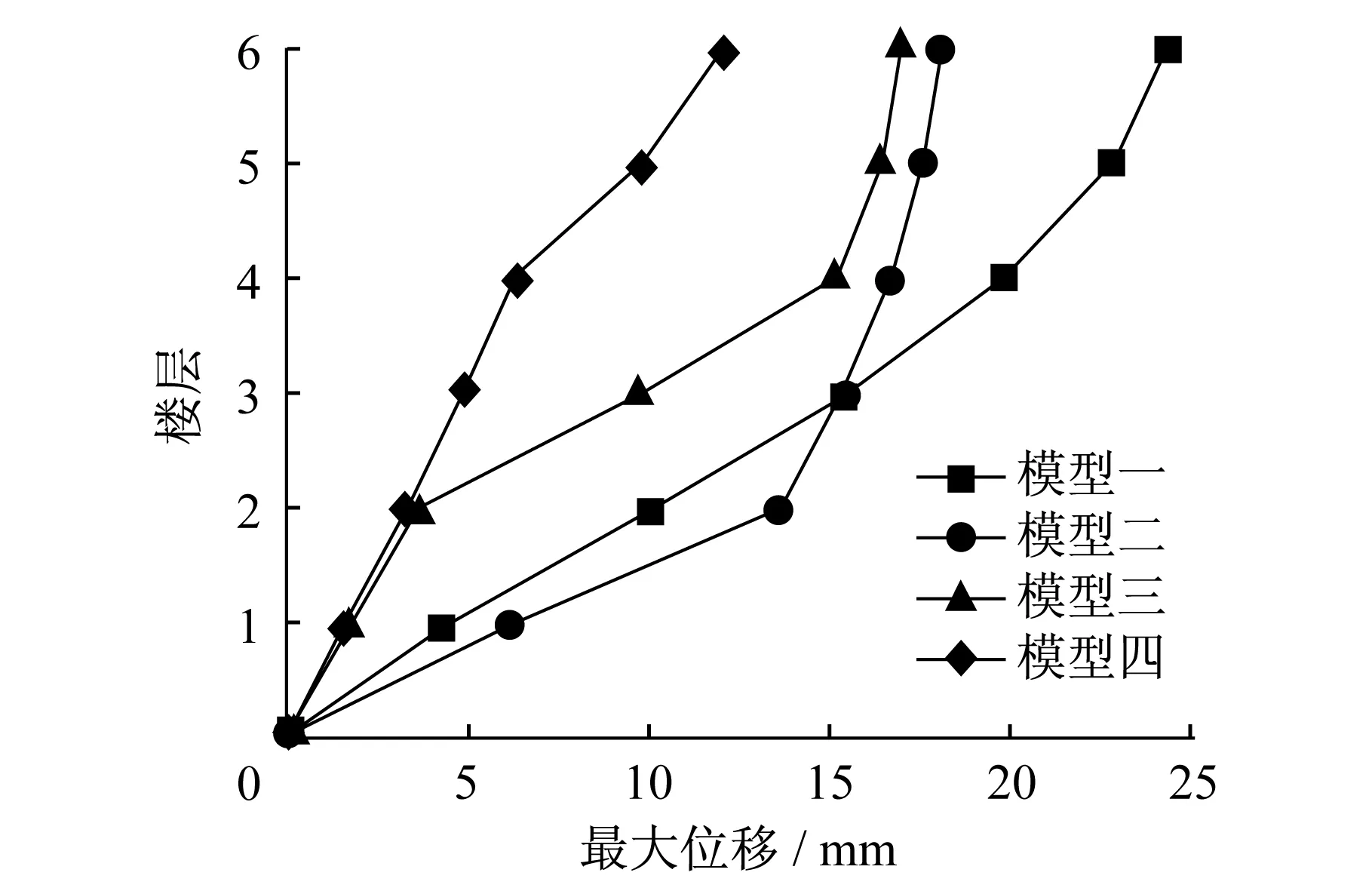
图4 各模型楼层最大水平位移Fig.4 Maximal horizontal displacement of each model

由图4可以看出,模型一最大水平位移曲线较为均匀连续,模型二至模型四分别在各自未布置墙体的楼层出现了位移的突变。以模型二为例,结构在一层和二层处变形较大,而在布置了填充墙的其他各层则变化均匀。

图5为各模型最大层间位移角信息。模型二、模型三、模型四布置了填充墙的楼层层间位移角均小于模型一纯框架下的层间位移角,说明填充墙的加入增加了结构的侧向刚度,减小了结构的地震反应。而模型二、模型三、模型四在结构竖向未布置填充墙的楼层,其层间位移角都发生了突变,且都超过了模型一下的层间位移角,说明结构在竖向刚度不连续的楼层产生的地震响应较为剧烈。这三种填充墙的竖向不规则布置中,模型二最为不利,其最大层间位移角为1/641,略小于规范限值1/550,虽然满足弹性层间位移角规范要求,但已经导致结构薄弱层的显现,在地震持续作用下,薄弱层将率先发生破坏。填充墙在竖向的不规则布置导致结构在竖向的刚度不均匀,在未布置墙体的楼层,刚度骤减,形成薄弱层。

图5 反应谱工况下各模型层间位移角Fig.5 Interlayer displacement angle of each model under response spectrum conditions

3.3 Pushover分析

Pushover分析即静力非线性分析,是一种基于性能的评估方法。本文所选用的侧向加载模式为基本振型加载和均匀加载,逐渐增加侧向力直至所选择的监测点达到所设定的位移或者倒塌。从侧向加载至结构失效的分析中,我们能够探究结构的薄弱层和破坏机制,从而为设计人员提供有效的结构信息[8]。

3.3.1塑性铰的力-位移曲线

图6为塑性铰的力-位移曲线。A为原点,B是塑性铰的屈服点,C点达到塑性铰的极限承载力,D点为塑性铰残余强度,E点表示塑性铰失效。在BC 段还有三个点IO(直接使用)、LS(生命安全)、CP(防止倒塌)代表塑性铰的三个能力水平。

图6 力-位移曲线Fig.6 Force-displacement curve

本文中框架柱选用PMM铰,框架梁选用M3塑性铰,分别定义在柱端和梁端。

3.3.2塑性铰的发展过程与分析

图7为纯框架结构塑性铰的发展过程。塑性铰首先出现在底部的梁端(图7(a));随着侧向荷载的增加,塑性铰向顶部楼层梁端发展,随后在一层柱底出现塑性铰(图7(b));随着继续加载,底部三层梁端的大部分塑性铰达到极限承载力,即将退出工作(图7(c))。

图8为底部两层不布置填充墙框架塑性铰的发展过程。塑性铰首先在未布置填充墙的底层梁端开展,而布置了填充墙的上部四层没有产生塑性铰(图8(a));随着侧向荷载的增加,未布置填充墙的两层梁端全部出现塑性铰,一层柱底和二层柱顶也出现了塑性铰,而上部四层梁、柱均未屈服(图8(b));继续加载,塑性铰开始向上层发展,但底部梁、柱部分塑性铰已经达到了承载能力极限,即将失效破坏(图8(c))。由于底部两层没有布置填充墙,上面四层满布,导致结构刚度在竖向不连续,下部较柔,虽然在一定程度上抑制了塑性铰向上部结构开展,但使得结构的塑性变形主要在底部两层集中发生,显然会加剧底部两层的破坏,与反应谱分析得出结论一致。

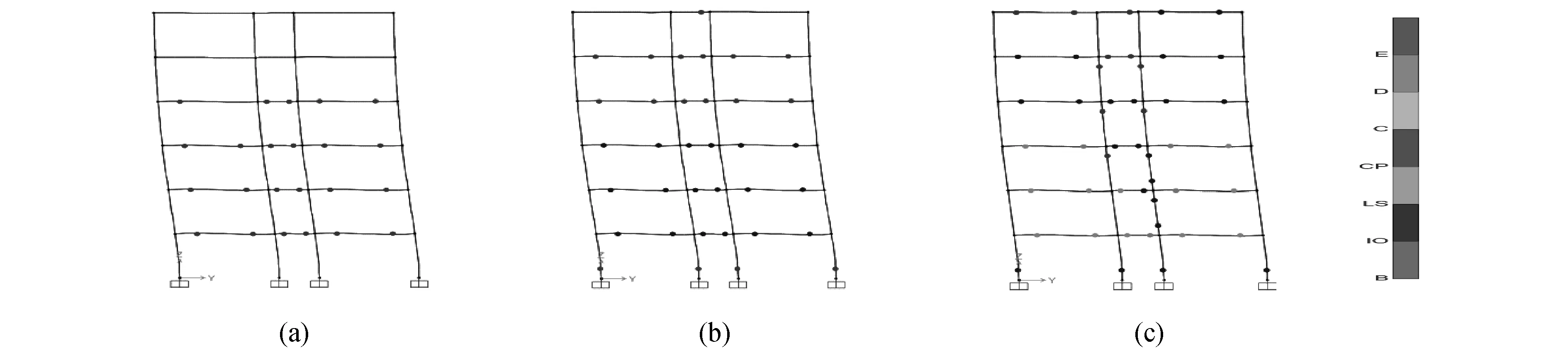
图7 模型一塑性铰的发展Fig.7 Plastic hinge development of model 1

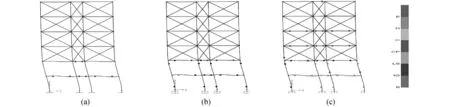
图8 模型二塑性铰的分布Fig.8 Plastic hinge development of model 2

图9为中间两层未布置填充墙框架塑性铰的发展过程。与模型二(图8(a))相似,塑性铰首先出现在未布置填充墙的楼层梁端(图9(a));随着侧向荷载增加,塑性铰向上部和下部楼层梁端开展,柱端塑性铰首先在三、四层中柱的柱底和柱顶产生,其他楼层柱子未屈服(图9(b));继续加载后,底部两层柱端也开始产生塑性铰,但是三层梁端塑性铰已经达到承载能力极限状态(图9(c)),结构将在中间薄弱层先行破坏。

图10为顶部两层未布置填充墙框架塑性铰的发展过程。塑性铰先在底部梁端和顶部梁端发展(图10(a));随着侧向荷载增加,所有梁端几乎都出现塑性铰,随后一层柱底出现塑性铰(图10(b));继续加载,底部梁端部分塑性铰达到极限承载力,即将失效退出工作(图10(c))。模型四塑性铰的发展过程没有出现明显的在未布置填充墙的顶部两层发生破坏的现象,这是由于结构顶部所受剪力较小,虽然未布置填充墙导致顶部较下部柔弱,但是顶部两层变形相对较小,其最终还是在底层先发生破坏。

图9 模型三塑性铰的分布Fig.9 Plastic hinge development of model 3

图10 模型四塑性铰的分布Fig.10 Plastic hinge development of model 4

3.3.3Pushover曲线以及性能点分析

对三个填充墙竖向不规则布置的模型进行Pushover分析,得到三条抗侧能力曲线,如图11所示。

图11 基底剪力-位移曲线Fig.11 Base shear force-displacement curves

根据能力谱法求得能力谱线与需求谱线的交点,即性能点。在罕遇地震下,模型二的性能点为(5 047 kN,63 mm),模型三性能点为(5 137 kN,55 mm),模型四性能点为(6 388 kN,49 mm)。三个模型在Pushover分析达到性能点时的层间位移角如图12所示。

图12 性能点处层间位移角Fig.12 Interlayer displacement angle at performance points

三种模型在性能点时的层间位移角规律和反应谱分析得到的相似,依旧表现为在各模型未布置填充墙的楼层层间位移角发生突变,且三种填充墙的不利布置中,模型二的竖向不规则布置在其薄弱层引起的地震响应最大。

4 填充墙竖向不规则布置的改进方案

由上述分析可知,填充墙的竖向不规则布置会导致结构产生薄弱层,使得结构在地震作用下偏于不安全。实际工程中常常可以见到结构底部作为商业用途很少布置填充墙的情况,即本文中模型二填充墙的布置形式,且这种布置形式在上述分析中最为不利,针对这种情况提出改进方案。出现薄弱层的本质原因是结构底部两层未布置填充墙使其侧向刚度较上部四层小,通过增大底部薄弱层框架柱的截面尺寸来提高其侧向刚度,即由原来的500 mm×500 mm增大为600 mm×600 mm,来减小刚度突变带来的不利影响。

4.1 改进方案的有效性分析

将改进前后的模型进行Pushover分析,得到改进前后模型的性能点分别为(5 047 kN,63 mm)和(6 005 kN,51 mm)。改进后的模型在达到性能点时监控点处的位移小于原模型,而基底剪力却比原模型高,说明结构的性能点提升,结构整体刚度变大,抗侧能力得到加强。

图13为改进前后模型达到性能点时的层间位移角。

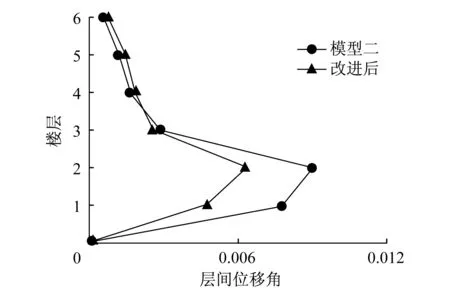
图13 性能点处层间位移角Fig.13 Interlayer displacement angle at performance points

增大底部两层框架柱截面尺寸后,结构在较为薄弱的一层和二层的层间位移角有了明显的降低。在推覆分析达到性能点时,模型二改进前后在第二层的最大层间位移角分别为0.009 01和0.006 33,地震响应降低幅度达到29.7%,说明通过增加框架柱截面尺寸这种方法行之有效。

5 结 论

(1) 弹性分析下,填充墙的加入增大了结构的侧向刚度,减小了结构的自振周期和层间位移,而未布置填充墙的楼层层间位移角均发生突变。填充墙在竖向的不规则布置导致结构在竖向的刚度不均匀,在未布置墙体的楼层,刚度骤减,形成薄弱层。

(2) Pushover分析下,填充墙对于结构的塑性铰有一定的抑制作用,其竖向不规则布置导致结构的塑性变形集中在薄弱层发生,这种集中效应显然会加剧薄弱层的破坏。

(3) 通过增大薄弱层框架柱截面尺寸,试图改善由于填充墙竖向不规则布置带来的不利影响,经过验证,该方案有效地降低了结构地震反应,方案简单可行,可为设计人员提供参考。

参考文献

[1] 周云,廖奕发,郭阳照,等.摩擦阻尼填充墙简易摩擦层性能试验研究[J].工程抗震与加固改造,2014,36(5):46-51.

Zhou Yun,Liao Yifa,Guo Yangzhao,et al.Performance experimental study on simple frictional damped layrer for frictional damped infill wall[J].Earthquake Resistant Engineering and Retrofitting,2014,36(5):46-51.(in Chinese)

[2] 周云,彭水淋,尹庆利,等.新型框架阻尼填充墙的设计与分析[J].工程抗震与加固改造,2010,33(4):79-83.

Zhou Yun,Peng Shuilin,Yin Qingli,et al.Design and analysis of a new infilled damping wall[J].Earthquake Resistant Engineering and Retrofitting,2010,33(4):79-83.(in Chinese)

[3] JGJ 3—2010 高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2010.

JGJ 3—2010 Technical specification for concrete structure of tall building[S] Beijing:China Building Industry Press,2010.(in Chinese)

[4] Polyakov S V.On the interactions between masonry filler walls and enclosing frame when loaded in the plane of the wall[J].Translations in Earthquake Engineering Research Institute,1956,125:558-562.

[5] Hashemi S A,Mosalam.Seismic evaluation of reinforced concrete buildings including effects of infill masonry walls[D].Pacific Earthquake Engineering Research Center,PEER,2007.

[6] 秦士洪,倪校军,曹桓铭,等.蒸压粉煤灰砖砌体应力-应变全曲线研究[J].建筑结构学报,2010,31(8):94-100.

Qin Shihong,Ni Xiaojun,Cao Hengming,et al.Research on stress strain full curves of autoclaved fly ash brick masonry[J].Journal of building Structures,2010,31(8):94-100.(in Chinese)

[7] 罗瑞,唐曹明,罗开海,等.常见填充墙竖向不均匀布置对框架结构抗震性能的影响研究[J].建筑结构,2016,46(3):24-31.

Luo Rui,Tang Caoming,Luo Kaihai,et al.Research on the influence of the vertical irregularities of infilled wall on the seismic performance of frame structures[J].Building Structure,2016,46(3):24-31.(in Chinese)

[8] 李碧雄.地震中砌体填充墙和RC框架梁柱协同作用机理[J].建筑结构,2015,45(4):97-101.

Li Bixiong.Interaction mechanism between masonry infilled wall and bounding RC frame under earthquakes[J].Building Structure,2015,45(4):97-101.(in Chinese)