评价桥墩地震自恢复能力的新指标及其应用

刘笑显 ,*

(1.同济大学土木工程防灾国家重点实验室,上海 200092; 2.中国公路工程咨询集团有限公司,北京 100089)

0 引 言

常规桥梁的抗震研究以及设计主要关注桥墩的延性,通过允许桥墩在地震中发生较大的位移来延长结构周期和耗散地震能量,防止桥梁在地震中倒塌。近期地震中的桥梁震害表明,虽然一些桥梁免于倒塌,但是由于墩顶残余位移过大而在震后丧失了使用性能[1]。通过对这些桥梁震害的重新认识,一些国家的学者提出了自恢复结构这一理念[2]。自恢复结构不仅允许构件在地震中进入非线性并通过构件滞回耗散地震能量,同时能在震后恢复到初始位置,从而减少或消除结构的残余变形。自恢复结构的滞回曲线一般呈旗帜形。与传统弹塑性结构相比,其能量耗散小、每个循环刚度变化频繁、残余位移小[3]。目前常见的自恢复结构的恢复力通常由无粘结预应力钢筋、自恢复框架支撑、形状记忆合金或结构自重来提供。

设置无粘结预应力钢筋的混凝土桥墩是桥梁领域常用的自恢复结构。Ikeda[4]进行了部分预应力混凝土柱的静力和拟动力试验,认为竖向预应力能有效减小强震下钢筋混凝土墩柱的残余位移。高婧[5]对节段拼装桥墩进行了研究,发现采用无粘结预应力钢筋的节段拼装桥墩残余位移较小,而采用耗能钢筋的节段拼装桥墩残余位移较大。Palermo[6]提出采用普通钢筋和无粘结预应力钢筋的混合配筋桥墩,发现其可以有效控制桥墩的峰值位移和残余位移。

拟静力循环分析是研究桥墩自恢复能力的常用方法[7-8]。Riddell和Newmark[9]发现残余位移的大小和滞回曲线形状密切相关。在桥墩从目标位移卸荷过程中,桥墩横向抵抗力恢复为零时的墩顶位移即为目标位移对应的拟静力残余位移[10]。拟静力残余位移代表了桥墩卸荷过程中能保持自身静力平衡的最大位移。地震作用下桥墩的残余位移小于拟静力残余位移。可以通过研究桥墩的拟静力残余位移来获得桥墩自恢复能力的影响因素及变化规律[7]。

目前国内外评价桥墩地震自恢复能力的指标主要有两类。一类指标是Hieber[11]针对设置无粘结预应力钢筋的钢筋混凝土柱提出的。该指标定义为轴向压力(包括预应力钢筋的预张力和静载)和截面粘结钢筋的屈服力之比。新西兰规范NZS3101[12]采用了该指标。但是该指标只针对设置无粘结预应力钢筋的钢筋混凝土柱,若结构中采用其他自恢复单元,则难以采用该指标进行评价。另一类指标是Kam[8]对由双线性弹塑性弹簧和双线性弹性弹簧并联成的理想旗帜形滞回模型分析提出了指标λ1,如图1所示。该模型是由设置无粘结预应力钢筋的桥墩简化得到。λ1定义为结构中弹性单元提供的恢复力和弹塑性单元提供的能量耗散力的比值。普通钢筋混凝土桥墩在其墩顶位移超过屈服位移时,桥墩底部钢筋和混凝土进入塑性,其墩底剪力-墩顶位移关系简化为双线性弹塑性模型,其提供的能量耗散力Fdis为屈服点的纵坐标,如图1(a)所示。无粘结预应力钢筋对桥墩的作用简化为双线性弹性模型[8],其提供的恢复力Frec为刚度折点纵坐标,如图1(b)所示。则λ1的表达式如式(1)所示。λ1值越大,桥墩自恢复能力越强。当λ1>1时桥墩拟静力残余位移较小,桥墩具有完全自恢复能力。但是该指标的求解要求结构中弹塑性构件和弹性构件对结构抵抗力的贡献可方便分离,且构件力学参数确定。对于实际结构,弹塑性构件和弹性构件在结构中共同作用,两者共同提供抵抗力,难以分别求解能量耗散力Fdis和恢复力Frec的数值,因此该指标在应用于实际结构时存在局限性。

图1 旗帜形模型组成Fig.1 Composition of flag-shape system

(1)

本文以一个由双线性弹塑性模型和双线性弹性模型并联而成的理想旗帜型滞回模型为背景,通过理论分析提出了实用的衡量桥墩自恢复能力的指标,建立了该指标和拟静力残余位移的关系。同时以一个实际单墩模型为算例,采用拟静力循环推拉分析和非线性时程分析方法,依据该指标检验预应力钢筋预张力、纵筋配筋率和预应力钢筋布置对桥墩自恢复能力的影响。

1 实用的自恢复能力指标的定义

定义新的自恢复指标S1为

(2)

(3)

(4)

(5)

当ap=0时,

(6)

此时S1与文献[8]中定义的指标λ1数值相等。

图2 旗帜形模型的分解Fig.2 Disintegration of flag-shape system

当要求结构具有完全自恢复能力时,即要求D点位于x轴上方:

(7)

(8)

此时拟静力残余位移为滞回曲线和x轴交点的横坐标。当D点位于x轴上方时,拟静力残余位移为

(9)

此时自恢复指标S1与拟静力残余位移xre有如下关系:

(10)

2 参数分析和算例

2.1 理想旗帜形滞回模型的自恢复性能的参数分析

选取一个单自由度理想旗帜形滞回模型进行拟静力循环加载分析。模型的各项参数初始值如下:双线性弹性弹簧刚度折点位移xe=0.08 m,第一刚度ke=25 000 kN/m,恢复力Frec=2 000 kN,第二刚度与第一刚度比值ae=0.05;双线性弹塑性弹簧屈服位移xp=0.05 m,初始刚度kp=40 000 kN/m,屈服力Fdis=2 000 kN,屈服后刚度比ap=0.05。对质点进行拟静力等幅强迫位移加载,位移幅值0.3 m。在模型性能评价时,主要对拟静力残余位移、等效阻尼比、λ1和S1进行分析和比较。

通过改变双线性弹性弹簧的第一刚度来改变其恢复力Frec,令其分别为0 kN (即模拟没有双线性弹性弹簧的工况)、1 000 kN、2 000 kN、3 000 kN,其余参数均为初始值。对模型进行强迫位移加载,模型的力-位移滞回曲线如图3所示,模型响应如表1所示。由图3和表1可知,当弹性弹簧恢复力增大后,拟静力残余位移减小,等效阻尼比减小,滞回曲线形状由平行四边形变化为旗帜形。当弹性弹簧恢复力由1 000 kN增大到2000 kN时,滞回曲线与x轴的交点由卸荷平台末端移动到刚度折点附近,因此拟静力残余位移减小显著。在弹性弹簧恢复力变化时λ1和S1均能反映结构恢复力和耗散力的相对大小关系。由于S1考虑了弹塑性弹簧的屈后刚度的自恢复贡献,因此各工况下S1均略大于λ1。

图3 不同恢复力时力-位移滞回曲线Fig.3 Force-displacement hysteresis of systems with varying restoring forces

表1 不同恢复力时模型性能Table 1 Properties of systems with varying restoring forces

改变双线性弹塑性弹簧的能量耗散力Fdis,令其分别为0 kN(即模拟没有弹塑性弹簧的工况)、1 000 kN、 2 000 kN、 3 000 kN,其余参数均为初始值。对模型进行强迫位移加载,模型的力-位移滞回曲线如图4所示,模型响应如表2所示。由图4和表2可知,当弹塑性弹簧屈服力增大后,结构的能量耗散力增大,λ1和S1相应减小,拟静力残余位移和等效阻尼比增大。当弹性弹簧屈服力由2 000 kN增大到3000 kN时,滞回曲线与x轴的交点由刚度折点附近移动到卸荷平台末端,因此拟静力残余位移增大显著。在弹性弹簧屈服力变化时λ1和S1均能反映结构恢复力和耗散力的相对大小关系。

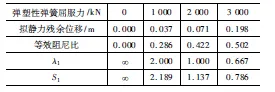
表2 不同能量耗散力时模型性能Table 2 Properties of systems with varying values of energy dissipation forces

图4 不同能量耗散力时模型力-位移滞回曲线响应Fig.4 Force-displacement hysteresis of systems with varying values of energy dissipation forces

改变弹塑性模型的屈后刚度比ap,令其分别为0.0、0.05、0.1、0.2,其余参数均为初始值。各情况下模型的力-位移滞回曲线如图5所示,模型响应如表3所示。由图5和表3可知,当弹塑性弹簧屈后屈前刚度比增大后,等效阻尼比和拟静力残余位移均减小,λ1始终保持不变而S1逐渐增大。在此过程中,只有指标S1能反映模型自恢复能力的变化。

图5 不同弹塑性弹簧屈服后刚度比时模型力-位移滞回曲线Fig.5 Force-displacement hysteresis of systems with varying values of post-yield stiffness ratio

表3 不同弹塑性弹簧屈后刚度比时模型性能Table 3 Properties of systems with varying values of post-yield stiffness ratio

对于实际桥墩,S1可以通过如下步骤求得:①对桥墩进行拟静力变幅循环推拉,最大位移为设定的目标位移,对桥墩的滞回曲线的包络线进行双线性化,如图6(a)所示,由此得到xe,双线性化的具体方法可以参考文献[15]附录A;②依据旗帜形滞回曲线中A点和D点横坐标相同,在目标位移对应的滞回曲线上绘制出直线x=xe,其与滞回曲线的两个交点的纵坐标分别为FA和FD,如图6(b)所示。最后按照式(2)计算得到S1。

图6 由滞回曲线得到S1Fig.6 Evaluating S1 from hysteretic loop

新指标S1的物理意义为结构中恢复力和能量耗散力的比值。当S1大于1.0时,结构残余位移小,自恢复能力强。当S1小于1并继续减小时,结构自恢复能力下降,残余位移迅速增加。可以采用该指标评价结构的自恢复能力。两结构的S1数值相同仅代表其自恢复能力相同,不能表明结构地震反应相同。与已有的自恢复指标λ1相比,新指标S1的优势主要体现在以下几点:①在实际结构中,自恢复构件和能量耗散构件相互耦合,新指标可以通过分析力-位移滞回曲线得到,避免了对能量耗散力Fdis和恢复力Frec的求解,因此可以直接应用于实际结构;②考虑了弹塑性构件的屈后刚度对结构自恢复性能的影响;③对于具有完全自恢复能力的结构可以从理论上建立自恢复指标和拟静力残余位移的关系。

2.2 无黏结预应力桥墩的自恢复性能研究算例

2.2.1模型介绍

选取一个设置无黏结预应力钢筋的混凝土桥墩验证S1的指标合理性并探索桥墩的自恢复能力影响因素。该模型各项参数初始值如下:桥墩高12 m,截面为圆形,半径R=1 m,保护层厚度5 cm。截面沿圆周布置有48根直径28 mm的钢筋,纵筋配筋率ρl=1%。箍筋直径18 mm,间距8 cm。纵筋和箍筋型号均为HRB400,屈服强度fy为400 MPa,混凝土采用C40混凝土,预应力钢筋为钢绞线。预应力钢筋面积0.015 4 m2,其布置在桥墩截面中心。预应力筋的预张拉力为P,预张力轴压比P/fc0Ag=0.05,其中fc0为混凝土轴心抗压强度,Ag为桥墩净截面积。墩梁固结,梁体简化为一个质点,质点质量m=343 000 kg。桥墩墩底固结。桥墩及模型示意图如图7所示。采用加州大学伯克利分校开发的抗震专业软件OpenSees (open system for earthquake engineering simulation)进行建模。建模时桥墩采用纤维单元[16]模拟,其中混凝土数值模型采用OpenSees中的concrete01模型,普通钢筋采用OpenSees中的steel02钢筋模型。预应力钢筋采用可以施加预应力的桁架单元,梁体质点通过刚臂与墩顶连接。在拟静力分析中,对梁体质点施加水平强迫位移,最大位移对应墩高的3%,即0.36 m。无黏结预应力钢筋对桥墩自恢复能力的贡献由两部分组成:无黏结预应力钢筋施加的轴向压力可以有效地限制墩身纵向钢筋的非线性拉应变[6,17],同时在桥墩大位移时预应力钢筋轴力的水平分力可以提供恢复力。由于前者涉及自恢复构件和能量耗散构件的相互作用,二者作用难以量化,因此较难计算自恢复指标λ1的数值。此处仅给出不同工况时的自恢复指标S1,通过残余位移的数值变化验证S1指标的合理性。

2.2.2地震波选取

采用来自太平洋地震工程中心的地震波数据库( PEER Strong Motion Database)的8组地震加速度记录,地震动参数如表4所示。在对桥墩地震残余位移进行参数分析中,采用峰值加速度调整为1.2g的地震动输入是因为此时桥墩峰值位移接近拟静力分析中的最大位移0.36 m。图8为地震动峰值加速度调整为1.2g后8条时程曲线对应的反应谱。在增量动力分析中,将8条地震波的峰值加速度从0.2g每隔0.2g增加到1.6g。模型的地震残余位移取8条地震波计算结果的平均值。

图7 桥墩及模型示意图Fig.7 Bridge column and analytical model

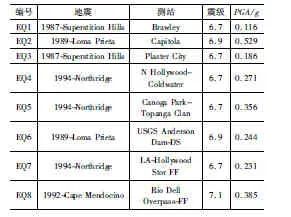
表4 地震动输入Table 4 Characteristics of considered seismic records

图8 加速度反应谱Fig.8 Acceleration response spectra

2.2.3预应力筋张拉力对桥墩自恢复能力的影响

改变预应力筋的张拉力,使预张力轴压比P/Fc0Ag分别为0、0.05、0.1、0.15,计算桥墩在拟静力循环荷载下的响应。拟静力分析结果如图9所示。在表5中,当P/Fc0Ag增大,桥墩的拟静力残余位移和地震残余位移减小,S1增大；同时桥墩的基底剪力增大,等效阻尼比减小。增量动力分析结果如图10所示,随着输入地震波峰值加速度的增大,地震残余位移增大。当预张力轴压比由0增加到0.05时,地震残余位移显著减小,随着预张力轴压比继续增加,地震残余位移减小幅度放缓。预张力轴压比为0.1和0.15两个工况时的地震残余位移相近。

图9 不同预张力下桥墩力-位移滞回曲线Fig.9 Hystereses of columns with varying prestressing force ratios

表5 不同预张力下桥墩性能Table 5 Properties of columns with varying prestressing force ratios

为了进一步研究残余位移随预张力轴压比的变化趋势,将预张力轴压比从0每隔0.01变化到0.2,拟静力残余位移和地震残余位移变化趋势如图11所示。随着预张力轴压比增加,残余位移先下降而后趋于平缓。当S1超过1时,残余位移下降速度放缓。因此为了有效提高桥墩自恢复能力,在设计无黏结预应力桥墩时,可以参考S1=1时预张力轴压比数值决定预张力的大小。

2.2.4普通钢筋配筋率对桥墩自恢复能力的影响

令桥墩的普通钢筋配筋率分别为0.25%、0.5%、1%和1.5%,计算桥墩在拟静力循环加载和增量动力分析的响应。拟静力分析结果如图12所示。在表6中,随着纵筋配筋率增大,桥墩的拟静力残余位移和地震残余位移增大,桥墩自恢复能力下降。当纵筋配筋率小于0.5%时,S1数值大于1,认为桥墩具有完全自恢复能力。增量动力分析结果如图13所示,当纵筋配筋率由1.5%降至0.5%,桥墩地震残余位移下降显著,若纵筋配筋率继续下降,地震残余位移下降幅度较小。考虑到配置无黏结预应力钢筋的桥墩由于轴压比较大,其屈服强度大于相应的普通桥墩,而减小纵筋配筋率可以降低桥墩屈服强度。因此将桥墩设计成配置无黏结预应力钢筋的桥墩时应减小纵筋配筋率,保证桥墩的屈服强度不变,从而在基础能力保护设计时不会提高基础的地震需求。

图10 不同预张力下桥墩地震残余位移的增量动力分析曲线Fig.10 IDA curves of earthquake residual displacements of columns with varying prestressing force ratios

图11 不同预张力轴压比下桥墩残余位移Fig.11 Residual displacement of columns with varying prestressing force ratios

2.2.5预应力钢筋布置对桥墩自恢复能力的影响

将预应力钢筋按照面积平均分为4束,对称布置在距截面圆心0.5倍半径和0.95倍半径处,具体布置如图14所示。拟静力分析结果如图15所示。随着预应力钢筋位置由圆心向圆周变化,拟静力残余位移下降了15%,等效阻尼比略有减小,最大剪力和屈后刚度增大,桥墩自恢复能力略有提高。增量动力分析结果如图16所示,在较大地震动激励时(PGA>0.8g),采用分散的预应力钢筋布置可以减小桥墩的地震残余位移。

图12 不同纵筋配筋率下桥墩力-位移滞回曲线Fig.12 Force-displacement hystereses of columns with varying longitudinal reinforcement ratios

表6 不同纵筋配筋率下桥墩性能Table 6 Properties of columns with varying longitudinal reinforcement ratios

图13 不同纵筋配筋率下桥墩地震残余位移的增量动力分析曲线Fig.13 IDA curves of earthquake residual displacements of columns with varying longitudinal reinforcement ratios

图14 预应力钢筋布置示意图Fig.14 Cross sections of columns with different strand configuration

图15 不同预应力钢筋布置时桥墩力-位移滞回曲线Fig.15 Force-displacement hystereses of columns with different strand configuration

表7 不同预应力钢筋布置下桥墩性能Table 7 Properties of columns with different strand configuration

图16 不同预筋布置下桥墩地震残余位移的增量动力分析曲线Fig.16 IDA curves of earthquake residual displacements of columns with varying strand configuration

3 结 论

(1) 以一个由双线性弹性弹簧和双线性弹塑性弹簧并联的理想旗帜形滞回模型为算例,增大弹性弹簧恢复力或弹塑性弹簧的屈服后刚度、减小弹塑性弹簧的能量耗散力均能减小残余位移,提高结构自恢复能力。

(2) 自恢复能力指标S1考虑了桥墩中弹性单元的恢复力、弹塑性单元屈服力和屈服后刚度对自恢复能力的影响,其可以通过公式计算或者对桥墩的滞回曲线分析求得该指标,而不必求出恢复力和耗散力的大小,因此其适用于实际结构。

(3)对设置无黏结预应力钢筋的桥墩进行分析,发现在一定范围内增大预应力钢筋的预拉力和减小普通钢筋的配筋率均可以显著减小桥墩残余位移,提高桥墩的自恢复能力。当自恢复能力指标S1大于1时,桥墩残余位移下降幅度放缓。因此在自恢复桥墩设计时,推荐S1取值等于1。采用分散的预应力钢筋布置时桥墩自恢复能力略有提高。

参考文献

[1] 刘丰,魏红一,王志强.PRC 桥墩抗震性能研究现状和展望[J].结构工程師,2007,23(5):48-51.

Liu Feng,Wei Hongyi,Wang Zhiqiang.State of the art of seismic performance of PRC bridge piers[J].Structural Engineers,2007,23(5):48-51.(in Chinese)

[2] 吕西林,陈云,毛苑君.结构抗震设计的新概念——可恢复功能结构[J].同济大学学报(自然科学版),2011,39(7):941-948.

Lü Xilin,Chen Yun,Mao Yuanjun.New concept of structural seismic design:earthquake resilient structures[J].Journal of Tongji University (Natural Science ),2011,39(7):941-948.(in Chinese)

[3] Christopoulos C,Filiatrault A,Bertero V V.Principles of passive supplemental damping and seismic isolation[M].IUSS Press,2006.

[4] Ikeda S.Seismic behavior of reinforced concrete columns and improvement by vertical prestressing[C].13th FIP Congress on Challenges for Concrete in the Next Millennium.1998,2:879-884.

[5] 高婧,葛继平,林铁良.干接缝节段拼装桥墩拟静力试验研究[J].振动与冲击,2011,30(4):211-216.

Gao Jing,Ge Jiping,Lin Tieliang.Pseudo static test for pre-cast segmental bridge columns with dry joints[J].Journal of Vibration and Shock,2011,30(4):211-216.(in Chinese)

[6] Palermo A,Pampanin S,Calvi G M.Concept and development of hybrid solutions for seismic resistant bridge systems[J].Journal of Earthquake Engineering,2005,9(6):899-921.

[7] Sakai J,Mahin S.Analytical investigations of new methods for reducing residual displacements of reinforced concrete bridge columns[R].Pacific Earthquake Engineering Research Center,University of California,Berkeley,CA,2004.

[8] Kam W Y,Pampanin S,Palermo A,et al.Self-centering structural systems with combination of hysteretic and viscous energy dissipations[J].Earthquake Engineering & Structural Dynamics,2010,39(10):1083-1108.

[9] Riddell R,Newmark N M.Statistical analysis of the response of nonlinear systems subjected to earthquakes[R].University of Illinois,Urbana,Illinois,1979.

[10] Cardone D.Re-centring capability of flag-shaped seismic isolation systems[J].Bulletin of Earthquake Engineering,2012,10(4):1267-1284.

[11] Hieber D G,Wacker J M,Eberhard M O,et al.Precast concrete pier systems for rapid construction of bridges in seismic regions[R].Washington State Department of Transportation Technical Report WA-RD,611,2005.

[12] SANZ,Concrete Structures Standard (NZS3101:2006)[S].Standards Association Wellington,NZ,2006.

[13] Katsaras C P,Panagiotakos T B,Kolias B.Restoring capability of bilinear hysteretic seismic isolation systems[J].Earthquake Engineering & Structural Dynamics,2008,37(4):557-575.

[14] 汤虎.中小跨径板式橡胶支座梁桥横桥向抗震设计理论与试验研究[D].上海:同济大学,2014.

Tang Hu.Experimental and theoretical research on transverse seismic deign of small and medium span bridges on elastomeric pad bearings[D].Shanghai:Tongji University,2014.(in Chinese)

[15] Chopra A K,Goel R K.A modal pushover analysis procedure to estimate seismic demands for buildings:theory and preliminary evaluation[R].PEER Report,2001.

[16] Mazzoni S,McKenna F,Scott M H,et al.OpenSees command language manual[J].Pacific Earthquake Engineering Research (PEER) Center,2006.

[17] Tobolski M J.Improving the design and performance of concrete bridges in seismic regions[D].University of California,San Diego,2010.