基于神经网络的钢绞线加固RC柱抗震性能评估
曹忠民
(华东交通大学土木建筑学院,南昌 330013)
0 引 言
高强钢绞线网-聚合物砂浆加固钢筋混凝土结构是近年发展起来的加固技术,具有显著提高加固构件刚度、耗能能力,耐火性能好,抗腐蚀、耐老化,对结构自重增加少等优点[1-2]。通过施加一定的预应力水平,可以有效地改善钢绞线应力滞后的现象,使得钢绞线的高强性能得到充分的发挥,同时也可以封闭已有裂缝和抑制其发展[3-5]。
延性是评价构件抗震性能的重要指标,良好的延性能避免构件发生脆性破坏,可以为构件在偶然超载作用下提供一定的安全储备[6]。目前,高强钢绞线网-聚合物砂浆加固钢筋混凝土结构已经在抗震加固领域受到关注,但关于其在工程实际中延性变形能力的研究还相对匮乏。
加固混凝土柱结构中的许多问题都是非线性的,影响混凝土柱延性的因素非常复杂,各因素对构件延性的影响存在一定的耦合作用。而人工神经网络具有联想推理、模拟思维和自适应识别的能力,通过学习可以找到输入-输出之间的映射关系[7-8]。因此,人工神经网络非常适合于结构工程中的非线性推理和预测。
人工神经网络中,BP神经网络与 RBF神经网络运用最为广泛。RBF神经网络是一种局部逼近网络,可以根据问题确定相应的网络拓扑结构,相比BP神经网络,具有学习速度快,有唯一确定的解,能获得全局最小点等优点,不存在BP网络中所遇到的局部极小值问题[9-10]。正是因为这些优良特性使得BP神经网络在越来越多的领域被RBF神经网络所替代。
鉴于以上情况,本文采用文献[4-5]中的试验数据结果,应用RBF神经网络得到高强钢绞线加固混凝土柱延性和各影响因素之间的映射关系,并用检验样本数据验证了神经网络的正确性。表明采用神经网络预测加固柱延性的可行性和准确性,在减少人为因素影响的同时,使得延性的计算更加高效、准确。本文在所提出方法的基础上,还对其延性进行了参数分析,所得结果可为此类问题的评定提供科学依据,并可供工程实际参考。
1 径向基神经网络基本原理
径向基神经网络示意图如图1所示,xi(i=1,2,3,…,m)为样本输入节点,m为输入节点个数。ti(i=1,2,3,…,r)为隐含层节点,r为隐含层节点的个数,可以根据网络训练算法的特点事先设定或者根据误差要求由网络训练时确定。wji为输入层到隐含层的权重,wki为隐含层到输出层的权重。yi(i=1,2,3,…,l)为样本输出。
其数学模型如式(1)所示:
(1)
(2)
式中:X为r维输入向量;ki为第i个隐节点中心;‖·‖通常为欧氏范数;θk为第k个输出节点的阀值;g(·)通常取为高斯函数,如(2)式所示。

图1 径向基网络结构示意图Fig.1 Structure of radial basis function neural network
RBF网络的学习算法由无导师学习和有导师学习两部分组成。无导师学习是对所有样本的输入进行聚类,求得各隐含层节点的RBF中心ki。当ki确定后,训练由隐含层至输出层之间的权值。
2 神经网络模型建立和预测
2.1 影响因素的灰色关联分析
对钢绞线加固RC柱建立神经网络模型时,首先要确定输入层变量,即影响钢绞线加固RC柱延性系数的主要因素,以取得更好的分析精度。本文拟采用灰色关联分析方法对各因素的影响程度进行量化,评价各因素与延性系数的相关性,以确定其主次影响因素,对输入层变量进行取舍。
灰色关联度分析法是一种因素比较分析方法,它通过数据序列曲线发展态势的相似程度来判断序列联系是否紧密,其紧密程度用关联度量化,进而寻求系统内部影响目标值的主要因素。数据序列曲线越接近,相应序列之间的关联度越大,反之就越小[11]。
(3)
设X0=(x10,x20,…,xh0)T为母序列(参数序列),取延性系数序列,X1=(x11,x21,…,xh1)T,X2=(x12,x22,…,xh2)T,…,Xq=(x1q,x2q,…,xhq)T为子序列(比较序列),分别取混凝土强度、轴压比、体积配箍率、钢绞线间距、预应力水平和剪跨比序列,h为实验数,取h=27,q为待分析的影响因素数,取q=6。则定义Xj与X0在第k点的关联系数为:
L0j(k)=(a+ρ·b)/(Δj(k)+ρ·b)
(4)

则Xj与X0之间的关联度为:
(5)
其大小即为各影响因素与延性系数的相关程度。文献[4-5]的试件主要数据见表1,关联度计算结果如表2所示。
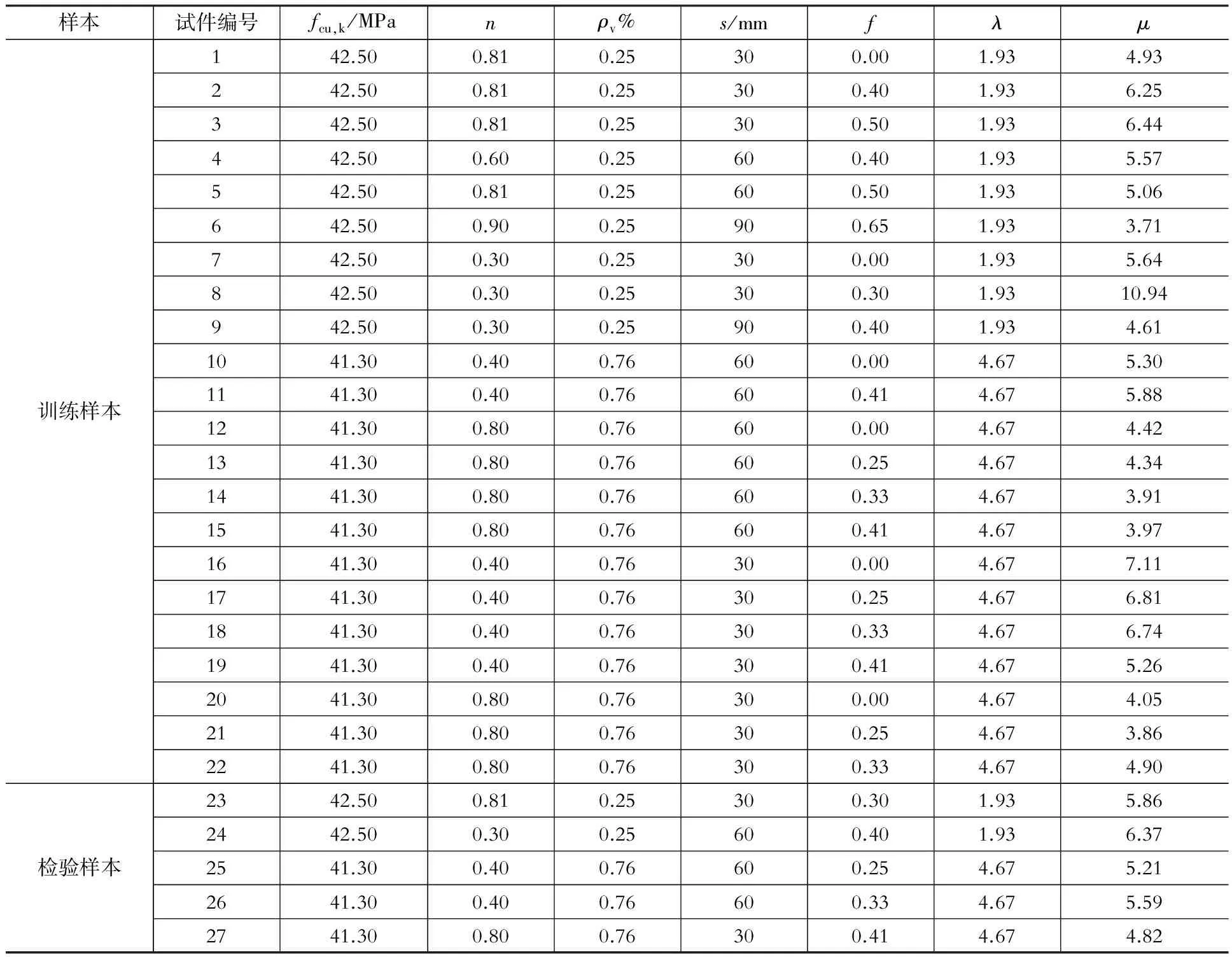
表1 试件主要数据Table 1 Primary data of specimens

表2 关联度分析结果Table 2 Analysis results of correlation
从表2中可以看出,关联度均介于0.50~0.63,说明本文取得各因素对钢绞线加固柱延性系数的影响均较大,而混凝土强度、钢绞线间距和预应力水平的关联性相对较强。
2.2 径向基神经网络模型的实现
RBF网络的实现过程如下:
(1) 选择主要影响因素。根据灰色关联分析的结果,输入参数取为6个,选择影响钢绞线加固RC柱延性的主要因素。
(2) 构造神经网络训练样本。由于RBF神经网络的训练是根据误差的大小来拓扑的,因此不存在训练样本个数的问题,只要其具有足够的代表性即可。根据文献[4-5]的试验结果,以其中22组数据作为训练样本,以5组无关数据作为检验样本。为减小网络训练误差,一般需在训练之前对训练样本进行归一化处理。
(3) 训练神经网络。把样本输入到精确的RBF神经网络中,并设定其确定输入单元个数,输出单元个数,扩展量spread,开始对网络进行训练。训练过程中,隐含层节点的个数不断地增加,直到达到最大节点个数或者达到误差要求时,训练完成,从而确定其隐含层节点个数和各权重值。其中,RBF神经网络参数的设定仅为一个,即spread,通过调试训练,本文取值为16。
(4) 用神经网络进行仿真。选定实测评价指标量,按输入样本的顺序组合成一个向量,输入到训练好的网络中得到相关信息。利用检验样本集,通过均方根误差(RMSE)和平均绝对误差(MAE)这两个指标对RBF神经网络进行评价,验证其应用于钢绞线加固RC柱延性预测的准确性。
(6)
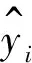
检验结果见表3,均方根误差(RMSE)为0.260 5,平均绝对误差(MAE)为0.043 9,训练得到的网络模型的预测值与试验值吻合较好。检验结果反映了神经网络模型的准确性,可用于延性的预测,而且,随着试验数据量的积累,该模型的模拟精度将进一步提高。
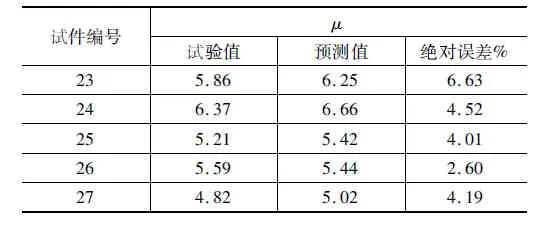
表3 样本检验Table 3 Sample test
3 神经网络模型的应用
由于试验量受到试验经费、工作量和时间期限等因素的影响,因此进行试件设计时往往采用正交试验设计等方法,以最少的试件、最小的人力和经费得到最多的数据。然而,当研究延性与影响因素间的变化规律时,得到的试验数据难以直接给出准确的变化趋势。利用训练好的神经网络模型,参照文献[5]试验中混凝土强度、剪跨比、体积配箍率的取值,考虑不同的轴压比、钢绞线间距和预应力水平三个参数,对钢绞线加固柱进行延性仿真模拟,实现在减少试验成本的前提下,更好地探究加固柱的延性规律。
3.1 轴压比的影响
轴压比对钢绞线加固柱延性的影响主要体现在两个方面。首先,试件截面边缘混凝土的主压应变及主压应力随着轴压比的增加而增大,从而导致试件的变形能力变差。其次,轴压比增大到一定程度后,由竖向荷载引起的P-Δ效应较明显,致使试件产生较大的附加变形,故达到最大荷载后,试件的稳定性与延性变差。
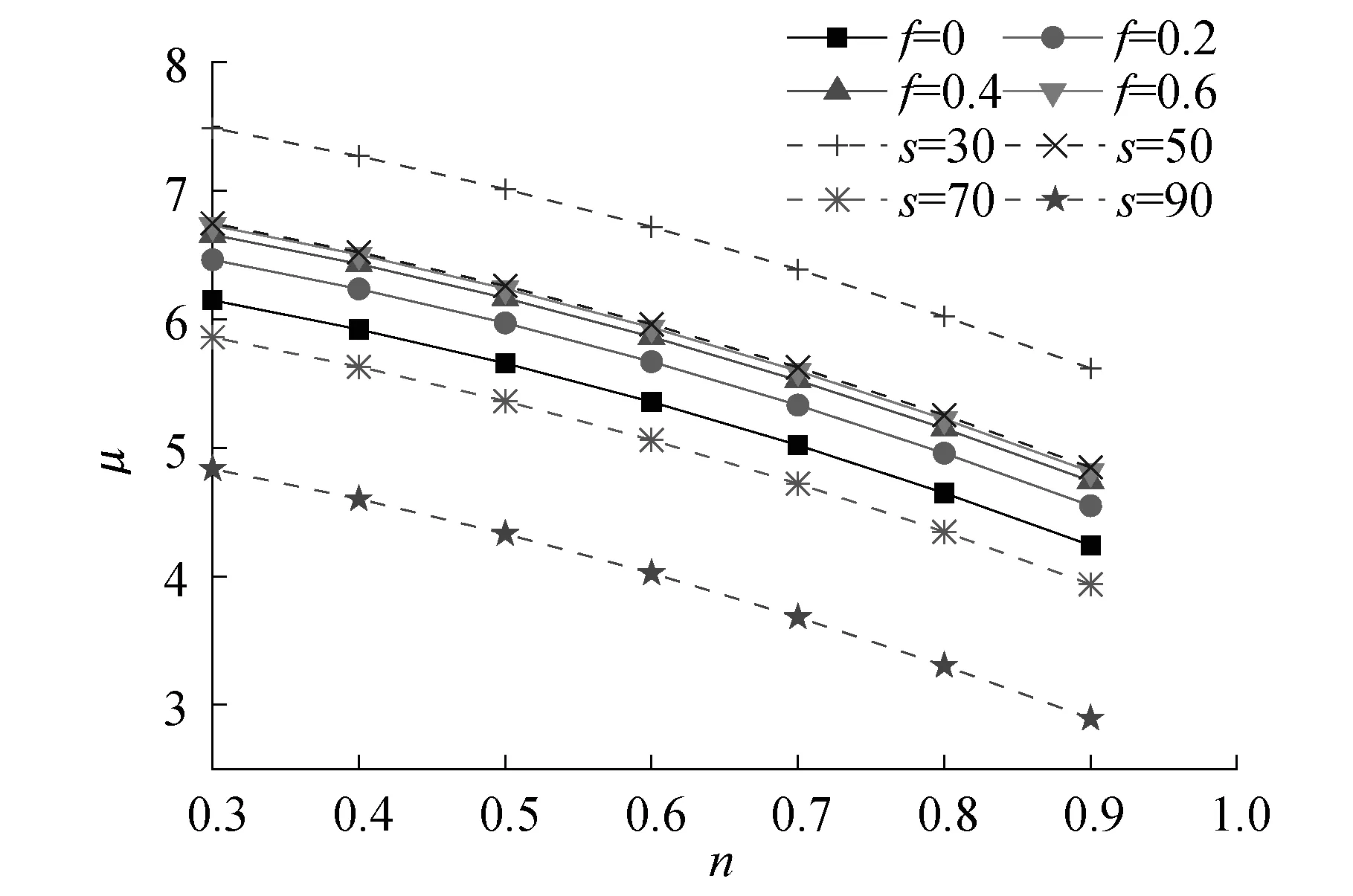
注:图中实线为试件钢绞线间距保持60, 虚线为试件预应力水平保持0.1
总体来说,随着轴压比的提高,加固柱的延性呈现快速下降。在同一轴压比情况下,预应力水平的提高,加固柱的延性增幅先大后小,整体呈上升趋势;钢绞线间距由密变疏,加固柱的延性呈下降趋势。对比可以发现,钢绞线间距的变化显著大于预应力水平对加固效果的影响,这和文献[4]中的结论不谋而合。由此可知,不论是长柱还是短柱,均有钢绞线间距变化对加固效果的影响显著大于预应力水平变化这一现象。
3.2 钢绞线间距的影响
配置钢绞线是体外配筋的一种形式,由于钢绞线对混凝土受力性能的改善,使得钢绞线加密对加固柱的延性产生积极影响。首先,试件的核心区混凝土在钢绞线的有效约束作用下,处于多向受力状态,使其极限变形能力得到提高。其次,通过配置钢绞线可以延缓外层混凝土和砂浆的脱落和剥离。
如图3所示,当预应力水平保持0.1时,随着轴压比的提高,钢绞线间距由密变疏,加固柱的延性呈快速下降趋势。而保持轴压比不变,随着预应力水平的提高,钢绞线间距对加固柱延性的影响趋势相同,限于篇幅,其图示从略。故当轴压比较高时,应配置较密的钢绞线,使得加固柱具有足够的抗震性能。

图3 延性与钢绞线间距的关系曲线Fig.3 Relation of ductility and space of steel wire
3.3 预应力水平的影响
预应力水平的施加,使得钢绞线的被动约束变为主动约束,可以有效改善被加固构件钢绞线应力滞后,充分发挥钢绞线的高强性能,同时也可以封闭已有裂缝和抑制其发展,对延性存在一定的影响。
如图4所示,当钢绞线间距保持60 mm时,随着预应力水平的提高,加固柱的延性呈现先升后降的趋势。当预应力水平小于0.4时是加固柱延性的变化较大;预应力水平以0.6为分界点,预应力水平小于0.6时提高对延性是有利的,预应力水平大于0.6时再提高将对延性不利。而保持轴压比不变,随着钢绞线间距变大,预应力水平对加固柱延性的影响趋势相同,限于篇幅,其图示从略。由于试验的局限性,文献[5]仅提出预应力水平不小于0.40时可获得较好的抗震性能,而通过神经网络研究其变化规律不仅可以弥补这一缺陷,而且可以便捷、高效地提供更为精确的结论以辅助相应的科学研究。

图4 延性与预应力水平的关系曲线Fig.4 Relation of ductility and prestressing level
4 结 论
(1) 本文结合27根钢绞线加固RC柱的试验数据首次应用神经网络预测钢绞线加固柱的位移延性,建立的径向基神经网络模型学习和预测的整体精度较高,在样本空间范围内,可较准确地预测在轴压比、钢绞线间距、预应力水平等因素影响下钢绞线加固RC柱的延性。故可用本文建立的径向基神经网络模型分析各因素对加固柱位移延性的影响规律。同时值得指出的是,本文建立的评估构件抗震性能的神经网络模型是动态的通过对实验数据量的积累,还可以进一步提高模型预测的精度和应用范围。
(2) 基于试验数据,利用灰色关联理论对延性的影响因素进行关联度分析,表明钢绞线间距和预应力水平对加固柱延性关联性较强。
(3) 该方法能够反映加固柱延性与影响因素间的非线性变化规律,随轴压比的提高而降低;随钢绞线间距由密变疏而降低;随预应力水平的提高而上升。不论是长柱还是短柱,钢绞线间距的变化对加固效果的影响显著大于预应力水平的变化;当剪跨比较小时,预应力水平以0.6为分界点,预应力水平小于0.6时提高对延性是有利的,预应力水平大于0.6时再提高将对延性不利。
(4)通过该模型进行仿真模拟,并结合试验数据,可在节约试验成本的前提下,更好地研究延性与影响因素间的变化规律,更准确地探究延性的变化趋势,为工程实际和抗震与优化设计提供参考。
参考文献
[1] 陈亮.高强不锈钢绞线网用于混凝土柱抗震加固的试验研究[D].北京:清华大学,2004.
Chen Liang.Experimental study of the seismic behavior of RC column strengthened with high strength steel wire[D].Beijing:Tsinghua University,2004.(in Chinese)
[2] Kim S H,Choi J H.Repair of earthquake damaged RC columns with stainless steel wire mesh composite[J].Advances in Structural Engineering,2010,13(2):393-402.
[3] 郭俊平,邓宗才,林劲松,等.预应力钢绞线网加固混凝土圆柱的轴压性能[J].工程力学,2014,31(3):129-137.
Guo Junping,Deng Zongcai,Lin Jinsong,et al.Axial compression performance of concrete columns strengthened with prestressed high strength steel wire mesh[J].Engineering Mechanics,2014,31(3):129-137.(in Chinese)
[4] 郭俊平,邓宗才,林劲松,等.预应力钢绞线网加固钢筋混凝土柱抗震性能试验研究[J].建筑结构学报,2014,35(2):128-136.
Guo Junping,Deng Zongcai,Lin Jinsong,et al.Experimental study on seismic behavior of RC colunms strengthened with prestressed high strength steel wire mesh[J].Journal of Building Structures,2014,35(2):128-136.(in Chinese)
[5] 邓宗才,李辉.预应力钢绞线加固混凝土短柱抗震性能研究[J].应用基础与工程科学学报,2014,22(5):941-951.
Deng Zongcai,Li Hui.Experiment study on the seismic behavior of RC short columns strengthened with prestessed steel wire[J].Journal of Basic Science and Engineering,2014,22(5):941-952.(in Chinese)
[6] 郑山锁,王帆,魏立,等.型钢高强混凝土框架柱位移延性系数研究[J].工业建筑,2014 (12):137-141.
Zheng Shansuo,Wang Fan,Wei Li,et al.Study of displacement ductility factor of steel reinforced high strength concrete frame columns[J].Industrial Construction,2014(12):137-141.(in Chinese)
[7] 冯清海,袁万城.BP 神经网络和 RBF 神经网络在墩柱抗震性能评估中的比较研究[J].结构工程师,2007,23(5):41-47.
Feng Qinghai,Yuan Wancheng.Comparative study on BP neural network and RBF neural network in performance evaluation of seismic resistance for pier columns[J].Structural Engineers,2007,23 (5):41-47.(in Chinese)
[8] 傅荟璇,赵红.MATLAB 神经网络应用设计[M].北京:机械工业出版社,2010,7.
Fu Huixuan,Zhao Hong.MATLAB neural network application design[M].Beijing:Mechanical industry press,2010,7.(in Chinese)
[9] Kim K B,Sim K B,Ahn S H.Recognition of concrete surface cracks using the ART1-based RBF network[J].Lecture Notes in Computer Science,2006 (3972):669-6751.
[10] 冯清海,袁万城.型钢高强混凝土柱抗剪承载力 RBF 神经网络预测方法及参数分析[J].结构工程师,2008,24(3):60-65.
Feng Qinghai,Yuan Wancheng.A method based on RBFNN to predict the shear strength of steel reinforced high-strength concrete columns[J].Structural Engineers,2008,24(3):60-65.(in Chinese)
[11] 刘思峰,谢乃明.灰色系统理论及其应用[M].北京:科学出版社,2008,12.
Liu Sifeng,Xie Naiming.Grey system theory and its application[M].Beijing:Science Press,2008,12.(in Chinese)

