近场地震下采用板式橡胶支座的简支梁桥横向位移控制

龚 ,*

(1.重庆交通大学土木工程学院,重庆 400074; 2.同济大学土木工程防灾国家重点实验室,上海 200092)

0 引 言

板式橡胶支座是中、小跨径梁桥使用最广泛的支座类型,通常直接放置在墩台的垫石上,而主梁则直接搁置在它上面。板式橡胶支座与垫石、主梁之间没有任何固定连接措施,而是通过接触面的摩擦力来防止三者在水平作用下的相对滑动。为了限制这种弱连接方式在地震中导致的大位移,在盖梁和台帽的两侧设置钢筋混凝土横向挡块是最常见的做法,挡块也因此被称之为“抗震挡块”。由于我国现行规范[1-2]对挡块的规定非常欠缺,挡块的功能定位、构造和配筋、设计方法等都没有成文的依据,导致板式橡胶支座+挡块这种连接方式的有效性被削弱。汶川震害调查表明,中、小跨径梁桥的典型横向震害是橡胶支座滑动产生过大的墩梁相对位移,造成挡块破坏,并进一步引发落座甚至落梁,而下部结构的损伤一般都较轻微[3]。因此,如何控制这类桥梁的横向位移成为近年来国内外的研究热点[4-9]。现有研究中,有些偏向研究板式橡胶支座的滑移效应[4-5],有些重点探讨挡块的作用及其合理参数取值[6-7],有些注重桥梁横向抗震设计理念和方法的改进[8-9]。总体来说,针对近场地震作用下桥梁横向位移控制方法的研究非常欠缺。在汶川地震中,许多发生严重横向位移震害的桥梁都位于断裂带附近,遭受了强烈的近场地震作用。有鉴于此,本文以汶川震区某简支梁桥为研究对象,基于OpenSEES开源平台,研究桥梁在汶川地震及典型近场地震波作用下的位移响应特征,探讨桥梁横向位移控制方法,以期对我国量大面广的中、小跨径梁桥提供抗震设计参考。

1 分析条件

1.1 桥例概况

本文选取映秀岷江桥作为研究桥例,该桥为213国道映秀至汶川方向的第一座桥,距断层不足100 m。在汶川地震中,该桥上部结构发生显著的移位,桥跨结构纵向脱离支座约20 cm,横向位移达140 cm,导致汶川岸的边梁掉落折断。如图1所示,该桥为4 m×30 m预应力混凝土简支T梁桥,横向设5片梁,桥宽10 m。每片T梁的两端各设置1个板式橡胶支座,中墩支座为GJZ400×400×99,边墩支座为GJZ300×300×85。双柱式圆形墩直径为1.5 m,两柱中心距为6.1 m,盖梁高1.5 m,宽1.7 m,长9.1 m。1#～3#墩分别高8 m、16 m和12 m。墩柱纵筋为30根φ36的HRB335钢筋,箍筋为φ18的光圆箍筋,墩柱两端的箍筋间距为115 mm。基础为桩柱式,直径1.8 m。主梁和盖梁采用C50混凝土,桥墩和基础分别采用C35和C30混凝土。

1.2 有限元建模

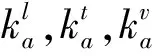
板式橡胶支座采用OpenSEES中的平滑动支座单元模拟,摩擦系数μ根据Coulomb理论假定在整个滑动过程中保持不变,不受滑动速度和支反力的影响。支座在竖向为只受压单元,即当支座受拉时,竖向刚度为零;受压时,竖向刚度为

(1)

如图3所示,支座在水平向上为双线性本构关系,水平刚度计算公式为

(2)

支座发生滑动时的临界摩擦力为

Fcr=μN

(3)

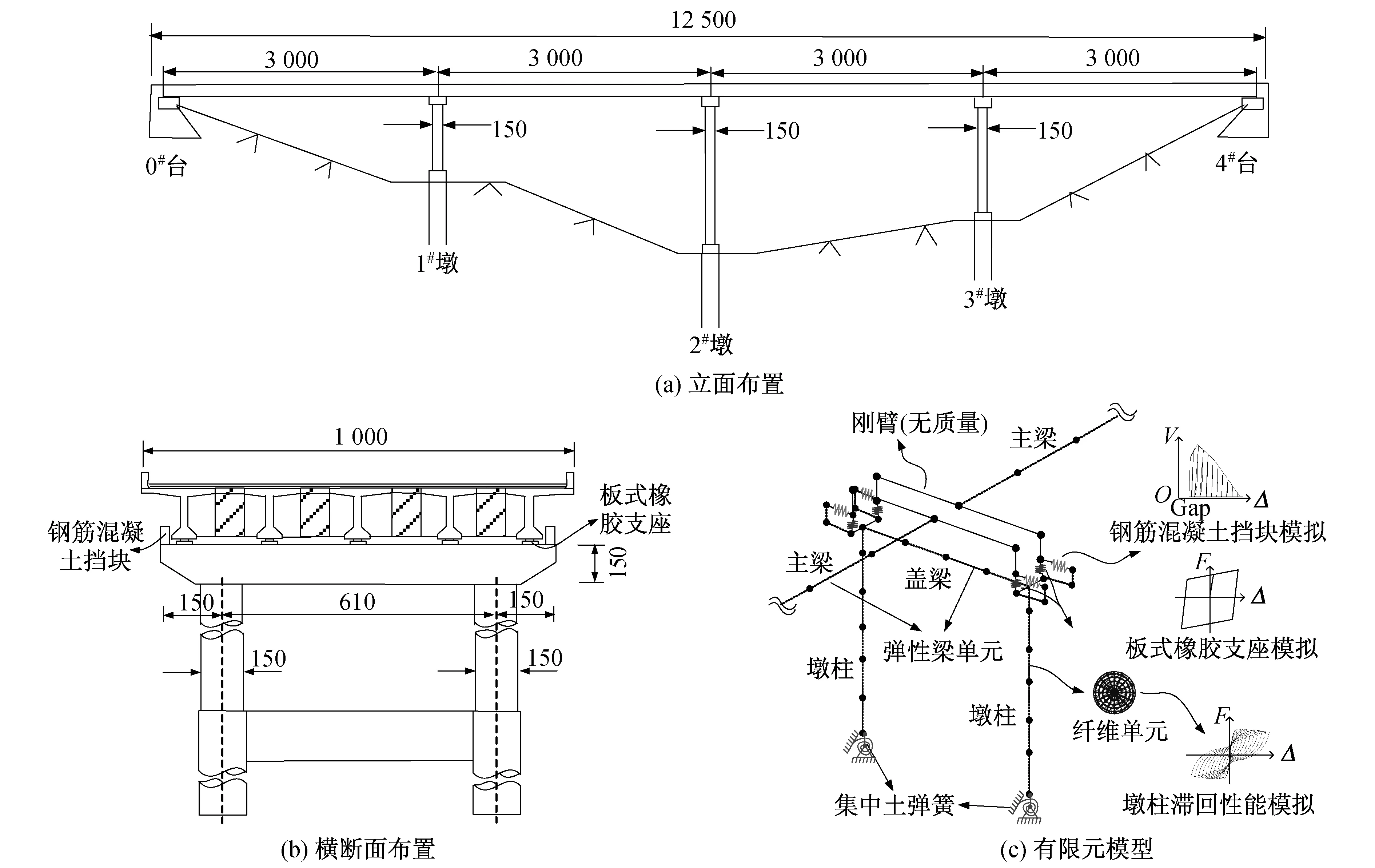
图1 桥例布置与有限元建模(单位:mm)Fig.1 Structural layout and finite element model of selected model (Unit:mm)

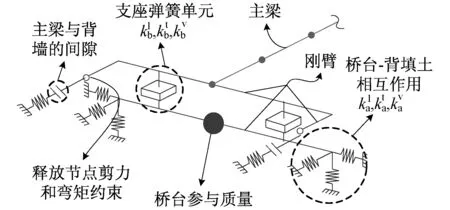
图2 桥台-背土作用模型[11]Fig.2 Model of abutment-backfill interaction

图3 支座模型Fig.3 Model of elastomeric bearing

桥例的原始设计采用钢筋混凝土挡块,根据文献[7]的研究成果,可采用如图4(a)所示的两分量弹簧模型模拟。其中,两分量弹簧分别代表混凝土贡献Vc和钢筋贡献Vs。在图4(a)中,V1对应挡块开裂时的强度;V2对应剪切钢筋屈服时的强度;V3对应剪切钢筋断裂时强度;V4对应混凝土贡献完全丧失时的强度;Δ1～Δ4分别对应挡块强度V1～V4时的变形;Δ5对应挡块的极限变形,此时剪切钢筋全部断裂,挡块彻底失效。上述参数的计算公式详见文献[7]。在实际工程中,挡块与梁体间存在间隙,为了模拟挡块与主梁之间的碰撞效应,挡块采用只受压的间隙单元模拟,由于混凝土挡块延性较低,容易脆断,因此忽略碰撞过程中的能量损失,采用如图1(c)所示的模型模拟。

为了进行对比,本文还对X形弹塑性钢挡块进行了研究。根据文献[12],弹塑性钢挡块的滞回曲线饱满圆滑,可近似采用双折线模拟,如图4(b)所示。弹塑性钢挡块可采用初始刚度K0、屈服强度Fy、屈服位移Δy和屈服后刚度比α这4个参数来表征。其中,屈服强度Fy可通过改变X型钢片的厚度和片数来调整,详见文献[12]。

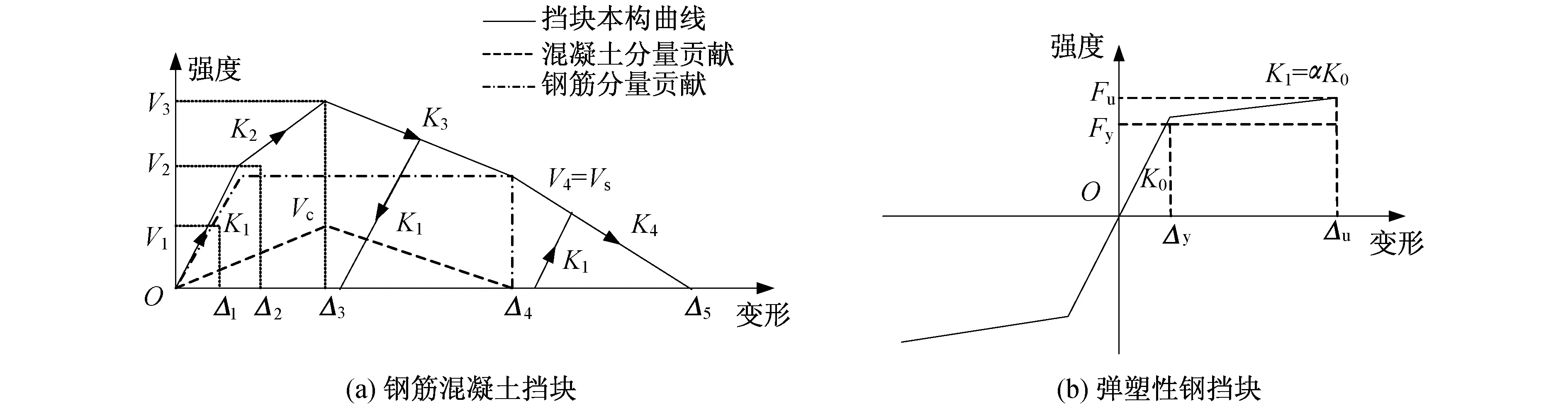
图4 挡块分析模型Fig.4 Model of side retainer

1.3 分析工况

在原始桥例中,钢筋混凝土挡块按照构造配筋,强度非常低,在地震中发生了剪断破坏,没有产生有效的限位效果。为了探讨两种挡块的位移控制效果,分析工况如下:

(1) 假设挡块非常弱,地震一开始就发生剪断破坏,分析时不考虑其有效贡献,后文简称“无挡块”工况。

(2) 沿用钢筋混凝土挡块,但对挡块进行加强。假设挡块的名义强度(图4(a)中的V3)分别等于各墩恒载支反力的20%和40%(美国Caltrans规范[13]建议30%,本文进行参数分析),挡块间隙分别为0.02 m和0.05 m,后文分别简称为“混凝土挡块20%-0.02 m”、“混凝土挡块40%-0.02 m”、“混凝土挡块40%-0.05 m”工况。

(3) 采用弹塑性钢挡块,使其屈服强度(图4(b)中的Fy)分别等于各墩恒载支反力的20%和40%。钢挡块与主梁通过螺栓连接,无间隙,后文分别简称“钢挡块20%”、“钢挡块40%”工况。

挡块的参数取值详见表1、表2。根据文献[7]的试验研究,混凝土挡块采用不同配筋时,尽管强度差别很大,但变形能力很接近。因此,本文仅仅改变其强度,不改变其变形能力。为了对比,将钢挡块的刚度K0人为设定成与混凝土挡块的K1相同。此外,本文在对结果进行分析时,为了直观对比,将“有挡块”的5个工况分别除以“无挡块”工况,进行标准化处理,后文将进一步详细。

表1 混凝土挡块关键参数取值Table 1 Parameter values of reinforced concrete retainers

表2 钢挡块关键参数取值Table 2 Parameter values of steel retainers

2 近场地震输入

近场地震具有滑冲效应、破裂方向性效应、速度大脉冲和上盘效应等特点,对桥梁结构具有极大的破坏力。本文选取汶川地震及国内外其他4条典型的近场地震动记录进行非线性时程分析,地震波沿着横桥向输入,不考虑竖向和纵桥向地震的影响。表3为6条地震波的基本信息。

图5为6条地震波的傅里叶幅值谱,该谱可反映地震动能量在频域内的分布情况。由图5可知,2条汶川波在高频带能量较丰富,且卓越频率也分布在较高的频率范围之内,即1.0～10.0 Hz;其余4条波主要在低频带能量较丰富,且卓越频率分布在较低的频率范围之内,即0.1～1.0 Hz。图6为6条地震波对应的加速度和位移反应谱。

表3 地震波基本信息Table 3 Basic information of selected ground motions

图5 各地震波的傅里叶幅值谱Fig.5 Fourier amplitude spectra of ground motions

图6 地震波加速度和位移反应谱Fig.6 Acceleration and displacement spectra of ground motions

3 结果分析

考虑到数据繁多,后文对6个工况、6条波的计算结果处理如下:对每一条地震波,以“无挡块”工况(对应原始桥例)为基准,将其余工况(“有挡块”工况)的结果分别除以“无挡块”工况,得到每一条地震波下“有挡块”工况对“无挡块”工况的比值。虽然本文在时程分析中没有对地震波进行调幅,但经过“比值”处理后,5个“有挡块”工况体现的是相对计算结果,即相对于原始桥例的位移控制效果。因此,对6条波的比值结果进行平均处理就合乎情理了。

3.1 支座变形分析

表4为采用混凝土挡块时支座的变形比值结果,由于是简支梁桥,因此每个墩都分别给出了两排支座的计算结果。由表可知,提高混凝土挡块的强度,可降低支座的变形;增大间隙可降低部分支座的变形,但同时也会引起其余支座变形增加。如对比“混凝土挡块20%-0.02 m”和“混凝土挡块40%-0.02 m”两个工况,增大挡块的强度使P2处支座的最大变形比下降75%左右,残余变形比下降77%～91%;对比“混凝土挡块40%-0.02 m”和“混凝土挡块40%-0.05 m”两个工况,增大间隙可使A0、P1上的支座最大变形比下降10%左右,残余变形比下降18%～54%。从数值上看,相对于“无挡块”,采用各种不同强度和间隙的混凝土挡块都只能降低部分支座的横向变形,同时还会增大其余支座的变形(比值大于1.0),说明混凝土挡块的位移控制效果较差。其原因在于混凝土挡块一方面改变了桥梁横向刚度和动力特性,进而改变桥梁的位移响应;另一方面混凝土挡块延性较低,容易发生剪断破坏而失去限位效果,因此它对桥梁位移的控制机理是两部分效应的叠加。图7和图8分别列举了P2墩上的支座与挡块在地震波NO.1作用下的力-变形关系响应曲线。由图可知,在“无挡块”和“混凝土挡块20%-0.02 m”两个工况下,支座均发生了明显的滑移,混凝土挡块也发生剪断破坏而完全失效;而在“钢挡块20%”工况下,支座的变形很小,钢挡块的滞回耗能对支座的限位效果非常显著。

表4 采用混凝土挡块时支座变形比Table 4 Deformation ratios of bearings when concrete side retainers used

混凝土挡块限位效果不太理想的主要原因是其变形能力和延性较差。表5为采用变形能力和延性更强的钢挡块得到的支座变形比值结果。与“无挡块”相比,所有支座的最大变形和残余变形都大幅降低,降幅最大超过90%。由图7(c)和图8(b)可知,采用钢挡块以后,支座的变形和滑移都得到限制,钢挡块的延性水平还未完全得到发挥。表明在相同强度下,变形能力和延性水平是提高挡块限位能力的关键指标。

图7 地震波NO.1作用下P2(P1侧)支座力-变形曲线Fig.7 Force-deformation curves of bearing at P2 (towards P1) underground motion NO.1

图8 地震波No.1作用下P2挡块力-变形曲线Fig.8 Force-deformation curves of side retainer at P2 under ground motion No.1

表5 采用钢挡块时支座变形比Table 5 Deformation ratios of bearings when steel side retainers used

3.2 主梁位移分析

图9和图10分别给出了在地震波No.1作用下主梁位移包络图和梁端位移时程图。采用混凝土挡块时,主梁位移呈现出“W”形。与“无挡块”相比,当混凝土挡块强度为20%时,两侧梁端附近的位移略有下降,但跨中附近的横向位移反而略有增大;当混凝土挡块强度达40%时,主梁的横向位移得到了一定程度的限制,梁端和跨中分别降低了17%和20%。对比“无挡块”、“混凝土挡块40%-0.02 m”和“混凝土挡块40%-0.05 m”可知,增大间隙会造成主梁横向位移的增大,跨中位移相比“无挡块”时增大了67%,说明增大挡块间隙虽然有助于橡胶支座柔性的发挥,但对主梁横向位移控制不利。采用钢挡块时,主梁位移呈现出“M”形,梁端位移大幅降低(图10),有效地保护了桥台处的支座(这是混凝土挡块无法做到的),尽管跨中附近的位移略有增大,但由于墩柱的柔性使墩上支座的变形明显小于桥台处的支座。因此,钢挡块对保护支座非常有效。

图9 主梁位移包络图(地震波No.1)Fig.9 Displacement envelope of girder (ground motion No.1)

图10 梁端位移时程图(地震波No.1)Fig.10 Displacement time history of girder end (ground motion No.1)

3.3 桥墩内力分析

表6列举了4个典型工况下双柱墩左、右墩底截面的内力与“无挡块”工况的比值。不论是采用混凝土挡块,还是钢挡块,都会增大墩底内力,且挡块强度越高,内力增幅越大。如对比“混凝土挡块20%-0.02 m”和“混凝土挡块40%-0.02 m”两个工况,混凝土挡块强度提高一倍以后,P1墩底弯矩和剪力比增大约43%;对比“钢挡块20%”和“钢挡块40%”两个工况,钢挡块强度提高1倍以后,P1墩底最大弯矩比提高34%,剪力比提高38%。与“无挡块”工况相比,虽然钢挡块的位移控制效果很好,但它会显著增大下部结构的内力响应,增幅远远超过混凝土挡块。原因在于钢挡块延性能力良好,在地震过程中始终保持对主梁的限制,不断将主梁的惯性力传递至下部结构;而混凝土挡块容易发生剪断破坏,传力能力有限。由此可见,采用挡块控制桥梁的横向位移,不宜盲目增大挡块的强度。

4 结 论

本文主要结论如下:

(1) 采用混凝土挡块进行位移控制时,不论是提高强度还是改变间隙,都无法保证所有支座不发生滑移,尤其是两侧桥台上的支座;采用钢挡块以后,强度只需要达到支反力的20%,就可以保证所有支座不发生滑移。说明变形能力和延性水平是挡块限位能力的关键指标。

表6 墩底截面内力比Table 6 Force ratios of pier base sections

(2) 采用混凝土挡块时,主梁的横向位移呈“W”形,提高挡块强度可使主梁位移下降,但两侧桥台处的位移始终无法得到控制;采用钢挡块时,主梁的横向位移呈“M”形,位移控制效果良好。

(3) 传统的混凝土挡块由于变形能力小、延性水平低,在近场地震下无法发挥位移控制作用。

(4) 挡块会增大墩柱的地震内力,挡块的强度越高,内力增幅越大,且钢挡块的增幅远远大于混凝土挡块。说明挡块限位效果越好,对下部结构的地震响应越不利。因此,采用挡块控制桥梁的横向位移时,其强度应经过慎重的设计优化。

参考文献

[1] JTG/TB 02-01—2008 公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.

JTG/TB02-01—2008 Guidelines for seismic design of highway bridges[S].Beijing:China Communication Press,2008.(in Chinese)

[2] JTG B 02—2013 公路工程抗震规范[S].北京:人民交通出版社,2014.

JTG B 02—2013.Specification of seismic design for highway engineering[S].Beijing:China Communication Press,2014.(in Chinese)

[3] 陈乐生,庄卫林,赵河清,等.汶川地震公路震害调查:桥梁[M].北京:人们交通出版社,2012.

Chen Lesheng,Zhuang Weilin,Zhao Heqing,et al.Report on highways’ damage in the Wenchuan Earthquake:bridge[M].Beijing:China Communications Press,2012.(in Chinese)

[4] 汤虎,李建中.地震动特性对公路桥梁板式橡胶支座滑动反应影响[J].工程力学,2013,30(10):154-161.

Tang Hu,Li Jianzhong.Effect of ground motion characteristics on sliding response of elastomeric pad bearings in highway bridges[J].Engineering Mechanics,2013,30(10):154-161.(in Chinese)

[5] 李悦,李冲,李茜.地震作用下板式橡胶支座滑移对中小跨径梁桥抗震性能的影响[J].土木工程学报,2014,47(S1):124-129.

Li Yue,Li Chong,Li Qian.Effect of elastomeric bearings slide on seismic performance of small and medium span girder bridges in earthquake[J].China Civil Engineering Journal,2014,47(S1):124-129.(in Chinese)

[6] Vasseghi A.Energy dissipating shear key for precast concrete girder bridges[J].Scientia Iranica A,2011,18(3):296-303.

[7] 徐略勤,李建中.挡块对规则连续梁桥横向地震反应的影响[J].公路交通科技,2013,30(4):53-59.

Xu Lueqin,Li Jianzhong.Effect of retainers on transverse seismic response of a standard continuous girder bridge[J].Journal of Highway and Transportation Research and Development,2013,30(4):53-59.(in Chinese)

[8] 王克海,韦韩,李茜,等.中小跨径公路桥梁抗震设计理念[J].土木工程学报,2012,45(9):115-121.

Wang Kehai,Wei Han,Li Qian,et al.Philosophies on seismic design of highway bridges of small or medium spans[J].China Civil Engineering Journal,2012,45(9):115-121.(in Chinese)

[9] 李建中,汤虎.中小跨径板式橡胶支座梁桥横向抗震设计研究[J].土木工程学报,2016,49(11):69-78.

Li Jianzhong,Tang Hu.Study on transverse seismic design of small and medium span bridges with elastomeric bearing pads[J].China Civil Engineering Journal,2016,49(11):69-78.(in Chinese)

[10] Mazzoni S,McKenna F,Scott M H,et al.Open system for earthquake engineering simulation:OpenSEES command language manual[M].California:University of California,Berkeley,2007.

[11] 徐略勤,乔万芝,何路平,等.地震下高墩刚构桥桥台-背土相互作用分析方法对比[J].土木建筑与环境工程,2016,38(6):105-112.

Xu Lueqin,Qiao Wanzhi,He Luping,et al.Comparison of analytical methods for the abutment-backfill interaction of a rigid frame bridge with high piers under seismic loading[J].Journal of Civil,Architectural & Environmental Engineering,2016,38(6):105-112.(in Chinese)

[12] 黄小国.连续梁桥防落梁装置试验和理论研究[D].上海:同济大学,2009.

Huang Xiaoguo.Experimental and theoretical research on unseating-prevention device for continuous bridges[D].Shanghai:Tongji University,2009.(in Chinese)

[13] SDC.Caltrans seismic design criteria version 1.7[S].California:California Department of Transportation,2013.