一种改进的混合蛙跳算法及其在变压器设计中的应用
杜 江,袁中华
(河北工业大学 电磁场与电器可靠性省部共建重点实验室,天津 300130)
变压器是应用最为广泛的电力设备之一,在电力系统中具有重要的地位,铁心柱截面设计为其设计过程中的重要一环.合理安排铁心级数及各级尺寸,使铁心柱更充分占用线圈内的圆形空间,即增大铁心柱截面积,可以达到节约生产材料、降低运行损耗的目的,具有非常重要的意义.目前常用的铁心柱截面优化设计方法有图解法、解析法、动态规划法等[1-2],但都存在设计结果粗糙、计算量大等问题,设计效果很难让人满意.
混合蛙跳算法[3](shuffled frog leaping algorithm, 简称SFLA)是结合模因算法(memetic algorithm, 简称MA)和粒子群优化算法(particle swarm optimization, 简称PSO)的一种全新智能仿生算法,具有结构简单、参数少、鲁棒性强等优点,一经提出便在计算机和工程领域得到广泛应用[4-6].然而,基本混合蛙跳算法(SFLA)只能求解无约束条件的优化问题,对有约束条件的优化问题,必须首先对约束条件进行处理.罚函数法[7]是目前最常用的约束条件处理方法,但是,常常因为罚因子选取不当,导致算法的搜索效率严重下降.另外,针对基本混合蛙跳算法易陷入局部最优、收敛精度不高的缺陷,国内外学者从不同角度进行了改进.文献[8]对算法的解向量进行离散化并采用阈值选择策略,增强了算法全局寻优能力,提高了收敛速度;文献[9]把加速因子引入子种群内部迭代,提高了算法整体寻优能力;文献[10]将差分进化有机地嵌入进化过程,改善了种群的多样性,提高了算法复杂问题寻优能力.笔者借鉴文献[11]的约束条件处理方法,引入移动步长变异算子,自适应调整移动步长,提出一种求解约束优化问题的自适应混合蛙跳算法(adaptive shuffled frog leaping algorithm for solving constrained optimization problems,简称CASFLA),且将此改进算法用于变压器铁心柱截面优化设计.
1 优化设计问题描述
变压器铁心柱截面优化设计就是在线圈内圆直径D和铁心级数n一定的情况下,合理安排铁心每级的片宽Bi和片厚Ti,使叠成后的铁心柱截面积达到最大.显然,级数越多,铁心柱截面就越趋近于圆形,铁心柱截面积就越大,线圈匝数就越少,就越节省材料;然而级数越多,铁心叠片的种类也就越多,铁心的制造工艺就越复杂.铁心柱直径与级数的对应关系如表1所示.

表1 铁心柱直径与级数的对应关系
1.1 目标函数
因为铁心柱截面积越大,越能节约材料、降低损耗,所以优化设计的目标函数为铁心柱截面积S最大,即
(1)
1.2 约束条件
(1) 铁心柱每级片宽必须为5的倍数,即
Bk%5=0.
(2)
(2) 第k级宽度一半的平方与从第1级(第1级记一半厚度)累加到第k级厚度平方之和,小于或等于线圈内圆半径的平方,即
(3)
(3) 考虑铁心柱与线圈间支撑件的存在,要求铁心柱第1级宽度不小于26 mm,第n级厚度不小于20 mm,即
B1≥26 mm,Tn≥20 mm.
(4)
(4) 第j级的宽度必须大于第j+1级宽度,即
Bj>Bj+1.
(5)
1.3 数学模型
根据上述分析可得到变压器铁心柱截面积优化设计的数学模型为
使得
(6)
2 改进的混合蛙跳算法
2.1 基本混合蛙跳算法
基本混合蛙跳算法寻优本质上是模拟自然界中青蛙的扑食动作.该算法的迭代可分为以下操作:种群混合排序、子种群划分和子种群内部更新.
设青蛙种群由分布在S维解空间内的F个青蛙个体组成,参与更新的青蛙个体属性由个体位置和移动步长来描述,它们分别为Xi=(xi1,xi2,…,xiS),Di=(di1,di2,…,diS),其中:1≤i≤m,-Dimax≤Di≤Dimax,Dimax为青蛙最大移动步长.
青蛙位置更新方法如下
Di=rand()×(X-Xw),
(7)
Xw(new)=Xw(old)+Di,
(8)
Xw(new)=Xw(old)+rand()×Dimax.
(9)
式(7)为移动步长公式,其中rand()为(0,1)之间的随机数.当式(8)为局部深度搜索时,X为子种群最优个体位置Xb;当式(8)为全局深度搜索时,X为整个种群最优个体位置Xg,Xw(old),Xw(new)分别为位置更新前后的青蛙个体位置.式(9)为随机移动公式.
根据适应度判断位置的优劣,每次更新均由子种群的最差个体参与,且每次更新只选择3种操作(局部深度搜索、全局深度搜索和随机移动)中的一种.
2.2 约束条件的处理
由前文对优化问题的描述可知,变压器铁心柱截面积优化设计是一个多约束条件优化问题.利用混合蛙跳算法求解约束优化问题,首先对约束条件进行处理,使其转化为无约束条件的优化问题.借鉴文献[11]约束条件的处理方法,使目标函数与约束条件分离,将原问题转化为
(10)
其中:fitness(x)对应优化问题的目标函数f(x);violation(x)对应优化问题的约束条件,反映解x对约束条件的违反程度;gi(x)是第i个不等式约束条件;hj(x)是第j个等式约束条件;p,q分别是优化问题中等式约束条件和不等式约束条件的个数.
在解空间内,满足所有约束条件的解x称为可行解,否则称为不可行解.基于以上对解x的适应度和对约束条件违反程度的规定,该文采用以下原则判断解空间内任意两个解(x1和x2)的相对优劣(以最小化问题为例):
(1) 当解x1和x2都为可行解,如果fitness(x1) (2) 当解x1和x2都为不可行解,如果violation(x1) (3) 当解x1为可行解,x2为不可行解,则x1优于x2. 对这类多变量、离散型、非线性、多约束条件的复杂优化问题,效仿遗传算法,添加变异操作机制,自适应改变移动步长,可以同时兼顾算法收敛速度及收敛精度,是一种非常有效的提高求解性能的方法.该文在种群进化的移动步长中引入变异算子,式(7)改写为 Di=rand()×di×(X-Xw), (11) 其中:di为移动步长变异算子. 由式(11)可以看出,变异算子的大小直接影响移动步长的大小,进而影响解空间的搜索范围.显然,di取值越大,搜索的解空间就越大;反之,搜索的解空间就越小.当算法处于迭代前期,较大的移动步长可以提高算法收敛速度,使蛙群迅速聚集在最优解附近;当算法处于迭代后期,较小的移动步长可在一定程度上避免粒子在最优解附近往复震荡,使算法更精确地收敛于最优解.另外,当算法最优解的进步速度较快时,较小的移动步长有助于避免粒子跳过解空间内的较优位置;当算法最优解的进步速度较慢时,算法很有可能陷入局部最优,此时较大的移动步长有助于算法跳出局部最优. 通过上述分析,该文最终确定了移动步长变异算子di的控制量为“算法迭代阶段测量值S”和“算法进步速度测量值V”.通过这两个控制量,共同决定di的取值. (1) 设t为当前算法的混合迭代次数(即进行全局信息交换次数),N1为预设算法的最大混合迭代次数.该文用比值t/N1表示算法所处的迭代阶段测量值S.设pmin,pmax为算法当前所处迭代阶段的阈值,且pmin∈[0,1),pmax∈(0,1],pmin≤pmax.当S∈[0,pmin] 时,则认为算法处于迭代前期,此时应使di取较大值,即扩大解空间搜索范围;当S∈(pmax,1]时,则认为算法处于迭代后期,此时应使di取较小值,以提高算法收敛精度并保证算法收敛;S∈(pmin,pmax]时,di取适中值. (2) 设Yg1,Yg2分别表示相邻两次混合迭代种群最优解,用它们的差(Yg2-Yg1)表示算法当前的进步速度.设Vmin,Vmax为算法进步速度的阈值,当(Yg2-Yg1)∈[0,Vmin],则认为进步速度较小,说明可能收敛于局部最优解附近,此时应使di取较大值,这样有助于算法跳出局部最优解;当(Yg2-Yg1)∈(Vmax,+∞)时,则认为进步速度较大,此时应使di取较小值,避免移动步长太大而漏掉解空间内较好的解;当(Yg2-Yg1)∈(Vmin,Vmax],即进步速度适中时,此时应使di取适中值. (3) 当这两个控制量的“意见”出现分歧时,应综合考虑这两个控制量对算法的影响,进而确定给变异算子di赋3个值(较大值dib、适中值dim和较小值dil)中的一个. 基于以上分析,并借助模糊控制思想,得到变异算子控制规则表(见表2). 表2 控制规则表 改进算法(CASFLA)对变压器铁心柱截面进行优化设计的步骤如下: 步骤1 对铁心柱参数(直径、级数等)、算法参数(种群规模、迭代次数、变异系数等)及青蛙种群个体位置进行初始化; 步骤2 计算每只青蛙个体的适应度或约束条件违反程度; 步骤3 对青蛙种群从优到劣进行排序; 步骤4 将该青蛙种群划分为m个青蛙子种群; 步骤5 对每个子种群进行指定次数的子种群内部更新; 步骤6 计算更新后每只青蛙的适应度或约束条件违反程度,并找出青蛙种群最优青蛙个体; 步骤7 如果算法当前迭代次数t<2,则执行步骤8;否则根据表1调整步长变异算子di的取值; 步骤8 判断是否满足结束条件,即判断是否达到最大混合迭代次数di或者满足最小允许误差Δ,如果不满足结束条件,则执行步骤3,否则输出变压器铁心柱优化结果并结束. 笔者将提出的求解带约束条件的自适应混合蛙跳算法(CASFLA)应用到3种典型直径的变压器铁心柱截面优化中,并与现有的算法比较,证实CASFLA的有效性. 首先以直径300 mm的铁心柱为例,CASFLA分别以8级和11级对300 mm的铁心柱截面积进行优化.算法参数为:青蛙个体数F=80,子种群数m=8,最大移动步长Dimax=0.3,最大混合迭代次数N1=100,子种群内部迭代次数N2=10;各控制参数为:pmin=0.5,pmax=0.75,Vmin=0.05,Vmax=0.5,dib=2,dim=1,dil=0.8;运行平台为Visual Studio 2010.对比结果如表3所示. 表3 不同算法300 mm铁心柱截面积优化结果比较 注:叠片系数为1,片宽以5结尾,直径偏差为0. 同样的方法对直径125,220 mm的铁心柱截面积进行优化设计,比较结果分别如表4,5所示. 表4 不同算法125 mm铁心柱截面积优化结果比较 注:叠片系数为1,片宽以5结尾,直径偏差为0. 表5 不同算法220mm铁心柱截面积优化结果比较 注:叠片系数为1,片宽以5结尾,直径偏差为0. 从表3~5可看出,采用笔者提出的改进算法(CASFLA)对变压器铁心柱截面积进行优化设计,得到的结果要优于其他算法.在计算复杂度方面,对Windows XP系统、AMD双核2.5 GHz CPU、1.94 G内存的计算机,混合迭代100次得到最优解所花费的时间仅为1.2 s左右,大大缩短了设计周期.另外,通过表4还可以看出,级数越大,越能得到更大的铁心柱截面积.在实际应用中,采用铁心柱截面优化设计结果,可节约生产材料、降低运行损耗,进而使综合经济效益进一步提高. 该文以铁心柱截面积最大为目标函数建立了变压器铁心柱截面优化设计模型,并结合混合蛙跳算法的特点,提出了一种求解约束优化问题的自适应混合蛙跳算法(CASFLA),且将其用于变压器铁心柱截面优化设计.3种典型直径变压器铁心柱截面优化设计结果表明,该算法具有更强的全局搜索能力,能增加铁心柱截面积,对节省材料、降低损耗有很大帮助. 参考文献: [1] 谢卫, 田程, 魏永国. 电力变压器铁心最佳截面的计算[J]. 上海大中型电机, 2010 (3): 8-9. [2] 王娟, 杨奕, 盛苏英. 电力变压器铁心柱截面的优化设计[J]. 变压器, 2011, 48 (9): 26-27. [3] EUSUFF M M, LANSEY K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Water Resour Plan Manage, 2003, 129 (3): 210-225. [4] 耿超, 王丰华, 苏磊, 等. 基于人工鱼群与蛙跳混合算法的变压器Jiles-Atherton模型参数辨识[J]. 中国电机工程学报, 2015, 35 (18): 4799-4807. [5] 张沈习, 陈楷, 龙禹, 等. 基于混合蛙跳算法的分布式风电源规划[J]. 电力系统自动化, 2013, 37 (13): 76-82. [6] 王介生, 高宪文. 基于改进蛙跳算法的电渣重熔过程多变量PID控制器设计[J]. 控制与决策, 2011, 26 (11): 1731-1734. [7] 龙文, 赵东泉, 徐松金. 求解约束优化问题的改进灰狼优化算法[J]. 计算机应用, 2015, 35 (9): 2590-2595. [8] 王茜, 张粒子, 舒隽, 等. 基于阈值选择策略的改进混合蛙跳算法在电网规划中的应用[J]. 电力系统保护与控制, 2011, 39 (3): 34-39. [9] ELBELTAGI E, HEGAZ Y T, GRIERSON D. A modified shuffled frog-leaping optimization algorithm application to project management[J]. Structure and Infrastructure Engineering, 2007, 3 (1): 53-60. [10] 赵鹏军, 邵泽军. 一种新的改进的混合蛙跳算法[J]. 计算机工程与应用, 2012, 48 (8): 48-50. [11] 王锡淮, 郑晓鸣, 肖健梅. 求解约束化问题的人工鱼群算法[J]. 计算机工程与应用, 2007, 43 (3): 40-42. [12] 王祝荣, 胡鹏, 孟庆民. 变压器铁心截面优化工程软件的开发[J]. 变压器, 2005, 42 (1): 1-3. [13] 汤赐, 张志文. 基因控制遗传算法在变压器铁心截面优化设计中的应用[J]. 变压器, 2006, 43 (2): 1-3.2.3 变异算子的引入
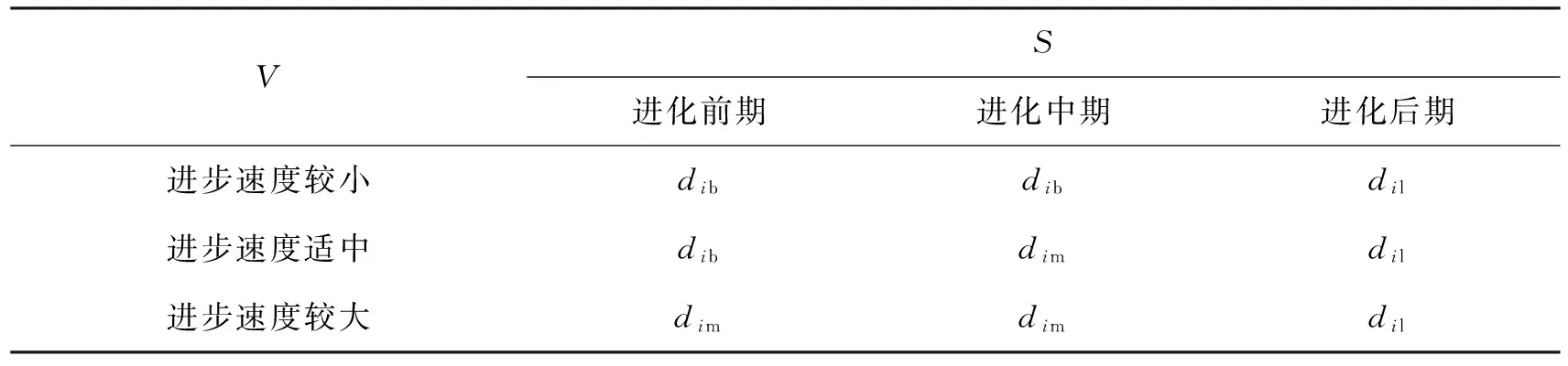
2.4 算 法
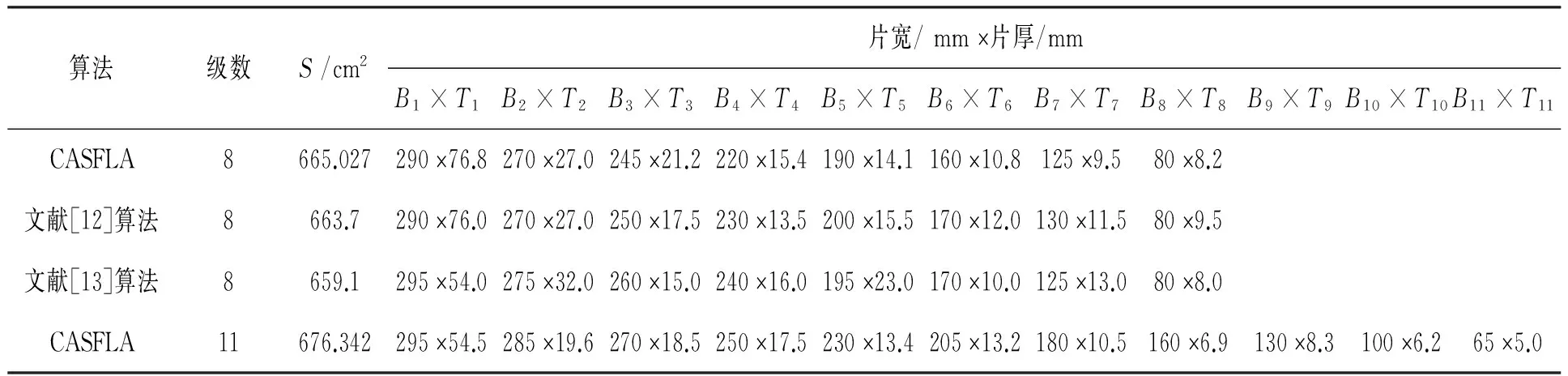
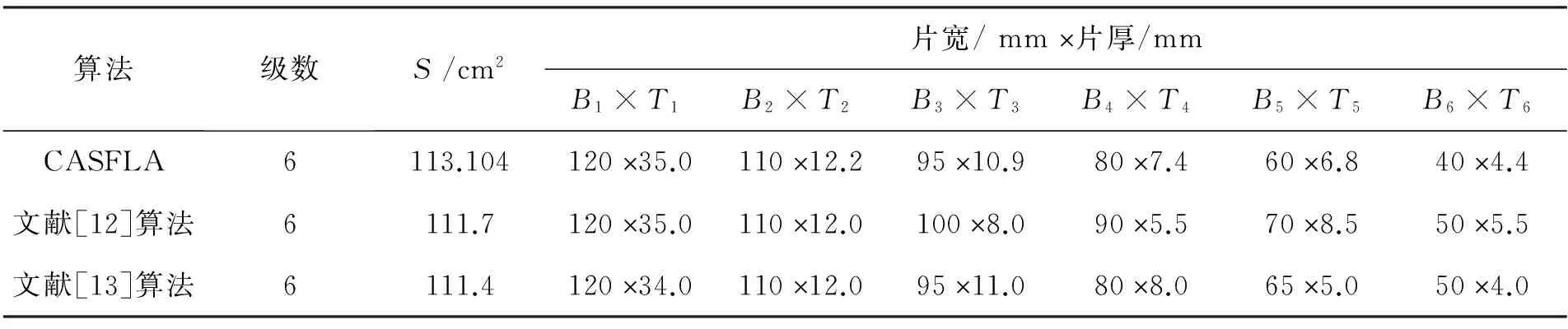
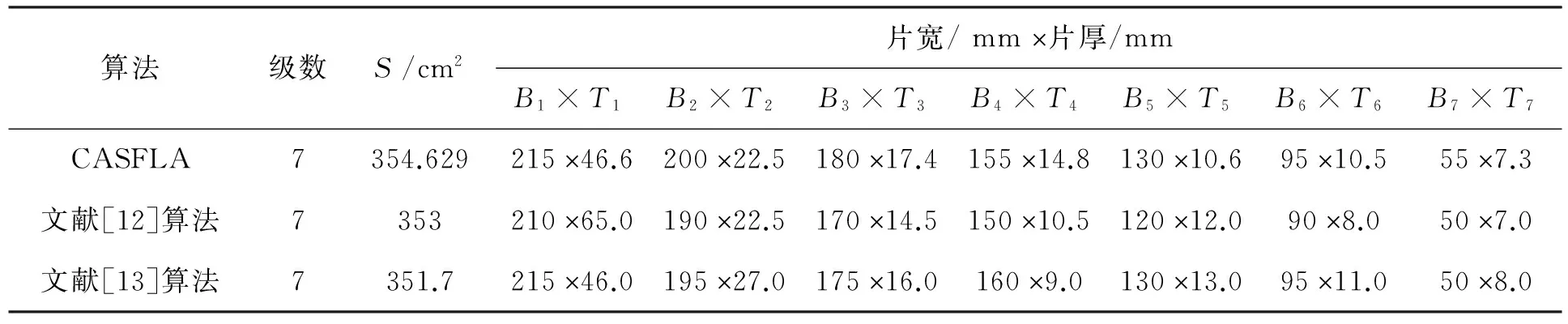
3 应用实例
4 结束语

