量子三元Werner态的抗噪声干扰特性

李国锋

(安徽大学 物理与材料科学学院，安徽 合肥 230039)

量子系统与周围环境发生相互作用是不可避免的，因此研究各种环境噪声对量子系统的作用是一件很有意义的事情，科研人员已研究噪声对量子系统的影响[1-2].另外，超纠缠的量子关联作为一种重要的量子资源，已引起人们极大关注[3-5]，这是因为其在未来的量子网络中有很多潜在应用，如态合并(state merging)[6-7]、远程态制备(remote state preparation)[8]、援助态辨别(assisted state discrimination)[9]和量子计算(quantum computation)[10-11].量子系统受环境噪声影响，其内在的量子关联也受环境噪声影响.通常情况下，噪声被认为总是损害(减少)量子系统的量子关联，而实际上并非如此，一些研究者已经发现某些特殊噪声在一定条件下能够增加系统的量子关联[12-13].研究人员的注意力集中到了所谓的关联动力学领域[14-15]，此领域的研究对象为开放系统及与其作用的环境，这些环境的作用可视为噪声.

谢传梅等[16]已研究两种噪声(移相噪声和旋转噪声)[17-18]对量子二元(qubit) Werner态量子关联的影响，其研究显示：在量子失协[3]和几何失协[4]框架下，量子关联在这两种噪声的作用下并不发生改变.笔者将考虑在量子失协和测量扰动框架下，量子三元(qutrit)Werner态的量子关联在移相噪声和旋转噪声作用下的行为.

1 量子三元Werner态

在考虑这两种噪声之前，先简单介绍一下量子三元Werner态.量子三元Werner态的表达式为

(1)

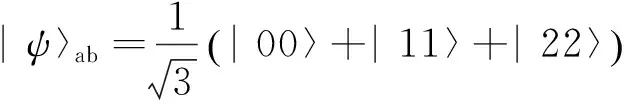
2 移相噪声作用下的量子三元Werner态

根据移相噪声的性质，经历一个移相噪声通道，量子三元的各元分别变为

|0〉→eiθ0|0〉, |1〉→eiθ1|1〉, |2〉→eiθ2|2〉,

(2)

其中：|0〉，|1〉，|2〉分别表示相应的态；θ0，θ1，θ2(均为实数)则分别表示在噪声的作用下这三态的相位变化.根据式(2)可得到

|00〉→ei2θ0|00〉， |01〉→ei(θ0+θ1)|01〉， |02〉→ei(θ0+θ2)|02〉，

|10〉→ei(θ1+θ0)|10〉， |11〉→ei2θ1|11〉， |12〉→ei(θ1+θ2)|12〉，

|20〉→ei(θ2+θ0)|20〉， |21〉→ei(θ2+θ1)|21〉， |22〉→ei2θ2|22〉.

(3)

经过严格的推导和计算，移相噪声作用后的量子三元Werner态变为

|11〉〈11|+e-i2γ01|11〉〈00|+e-i2γ02|22〉〈00|+e-i2γ12|22〉〈11|+|22〉〈22|].

(4)

通过近一步的观察，发现方程(4)还可以写成

(5)

其中：U=eiφ0|0〉〈0|+eiφ1|1〉〈1|+eiφ2|2〉〈2|是单粒子幺正算符，且φ0=θ0-θ1-θ2，φ1=θ1-θ0-θ2，φ2=θ2-θ0-θ1.从式(5)可知： 移相噪声对量子三元 Werner态的作用等价于局域幺正操作.文献[19]明确指出：任意局域幺正操作下的Werner态，其量子关联不因操作改变，所以可以得到如下结论：经过移相噪声作用后的量子三元 Werner态，其量子关联量值不发生改变.

3 旋转噪声作用下的量子三元Werner态

3维空间的任意角度的旋转可分解为3个垂直方向的定轴平面旋转.在旋转噪声通道中，旋转被加到量子三元的每一元上，即

(6)

其中

(7)

逐项考虑各平面(2维)旋转对各元的影响，将3平面旋转叠加起来就是综合效果.考虑噪声分量R3(γ)作用下两体矢量的改变，在旋转噪声分量R3(γ)作用下，新产生的矢量(箭头右边)与原矢量(箭头右边各项)的关系为

(8)

其中：γ为|0〉，|1〉因噪声扰动而旋转的角度，且为实数.

经过繁琐的多步计算，可得到

|00〉〈00|→cos4γ|00〉〈00|+sinγcos3γ|00〉〈01|+sinγcos3γ|00〉〈10|+sin2γcos2γ|00〉〈11|+

sinγcos3γ|01〉〈00|+sin2γcos2γ|01〉〈01|+sin2γcos2γ|01〉〈10|+sin3γcosγ|01〉〈11|+

sinγcos3γ|10〉〈00|+sin2γcos2γ|10〉〈01|+sin2γcos2γ|10〉〈10|+sin3γcosγ|10〉〈11|+

sin2γcos2γ|11〉〈00|+sin3γcosγ|11〉〈01|+sin3γcosγ|11〉〈10|+sin4γ|11〉〈11|，

(9)

|01〉〈01|→sin2γcos2γ|00〉〈00|-sinγcos3γ|00〉〈01|+sin3γcosγ|00〉〈10|-sin2γcos2γ|00〉〈11|-

sinγcos3γ|01〉〈00|+cos4γ|01〉〈01|-sin2γcos2γ|01〉〈10|+sinγcos3γ|01〉〈11|+

sin3γcosγ|10〉〈00|-sin2γcos2γ|10〉〈01|+sin4γ|10〉〈10|-sin3γcosγ|10〉〈11|-

sin2γcos2γ|11〉〈00|+sinγcos3γ|11〉〈01|-sin3γcosγ|11〉〈10|+sin2γcos2γ|11〉〈11|，

(10)

|10〉〈10|→sin2γcos2γ|00〉〈00|-sinγcos3γ|00〉〈01|+sin3γcosγ|00〉〈10|-sin2γcos2γ|00〉〈11|-

sinγcos3γ|01〉〈00|+cos4γ|01〉〈01|-sin2γcos2γ|01〉〈10|+sinγcos3γ|01〉〈11|+

sin3γcosγ|10〉〈00|-sin2γcos2γ|10〉〈01|+sin4γ|10〉〈10|-sin3γcosγ|10〉〈11|-

sin2γcos2γ|11〉〈00|+sinγcos3γ|11〉〈01|-sin3γcosγ|11〉〈10|+sin2γcos2γ|11〉〈11|，

(11)

|11〉〈11|→sin4γ|00〉〈00|-sin3γcosγ|00〉〈01|-sin3γcosγ|00〉〈10|+sin2γcos2γ|00〉〈11|-

sin3γcosγ|01〉〈00|+sin2γcos2γ|01〉〈01|+sin2γcos2γ|01〉〈10|-sinγcos3γ|01〉〈11|-

sin3γcosγ|10〉〈00|+sin2γcos2γ|10〉〈01|+sin2γcos2γ|10〉〈10|-sinγcos3γ|10〉〈11|+

sin2γcos2γ|11〉〈00|-sinγcos3γ|11〉〈01|-sinγcos3γ|11〉〈10|+cos4γ|11〉〈11|，

(12)

|00〉〈11|→sin2γcos2γ|00〉〈00|-sinγcos3γ|00〉〈01|-sin3γcosγ|00〉〈10|+sin4γ|00〉〈11|-

sin3γcosγ|01〉〈00|-cos2γcos2γ|01〉〈01|-sin2γcos2γ|01〉〈10|+sinγcos3γ|01〉〈11|+

sin3γcosγ|10〉〈00|-sin2γcos2γ|10〉〈01|-sin2γcos2γ|10〉〈10|-sin3γcosγ|10〉〈11|+

cos4γ|11〉〈00|+sinγcos3γ|11〉〈01|+sinγcos3γ|11〉〈10|+sin2γcos2γ|11〉〈11|，

(13)

|11〉〈00|→sin2γcos2γ|00〉〈00|+sin3γcosγ|00〉〈01|+sin3γcosγ|00〉〈10|+sin4γ|00〉〈11|-

sinγcos3γ|01〉〈00|-sin2γcos2γ|01〉〈01|-sin2γcos2γ|01〉〈10|-sin3γcosγ|01〉〈11|-

sinγcos3γ|10〉〈00|-sin2γcos2γ|10〉〈01|-sin2γcos2γ|10〉〈10|-sin3γcosγ|10〉〈11|+

cos4γ|11〉〈00|+sinγcos3γ|11〉〈01|+sinγcos3γ|11〉〈10|+sin2γcos2γ|11〉〈11|，

(14)

|02〉〈02|→cos2γ|02〉〈02|+sinγcosγ|02〉〈02|+sinγcosγ|12〉〈02|+sin2γ|12〉〈12|，

(15)

|12〉〈12|→sin2γ|02〉〈02|-sinγcosγ|02〉〈02|-sinγcosγ|12〉〈02|+cos2γ|12〉〈12|，

(16)

|20〉〈20|→cos2γ|20〉〈20|+sinγcosγ|20〉〈21|+sinγcosγ|21〉〈20|+sin2γ|21〉〈21|，

(17)

|21〉〈21|→sin2γ|20〉〈20|-sinγcosγ|20〉〈21|-sinγcosγ|21〉〈20|+cos2γ|21〉〈21|，

(18)

|00〉〈22|→cos2γ|00〉〈22|+sinγcosγ|01〉〈22|+sinγcosγ|10〉〈22|+sin2γ|11〉〈22|，

(19)

|11〉〈22|→sin2γ|00〉〈22|-sinγcosγ|01〉〈22|-sinγcosγ|10〉〈22|+cos2γ|11〉〈22|，

(20)

|22〉〈00|→cos2γ|22〉〈00|+sinγcosγ|22〉〈01|+sinγcosγ|22〉〈10|+sin2γ|22〉〈11|，

(21)

|22〉〈11|→sin2γ|22〉〈00|-sinγcosγ|22〉〈01|-sinγcosγ|22〉〈10|+cos2γ|22〉〈11|，

(22)

|22〉〈22|→|22〉〈22|.

(23)

把式(9)～(23)代入方程(1)，可发现受到旋转噪声分量R3(γ)作用后的量子三元Werner态并没有发生改变，即

(24)

类似地，可以得到

(25)

(26)

显然，可以得到

(27)

也就是说旋转噪声作用后的量子三元Werner态仍然为量子三元Werner态，等价于态整体发生了空间旋转，各相对矢量之间的关系没变.

4 结束语

笔者研究了在移相噪声和旋转噪声作用下的量子三元Werner态，结果表明：这两种噪声不改变量子三元Werner态中的量子关联.换句话讲，量子三元Werner态的量子关联具有抵抗噪声扰动的特性，这一结果与文献[16]的互为印证，并把研究结论从量子二元Werner态推广到量子三元Werner态.文献[20]在度量量子三元Werner衍生态量子关联的过程中，忽略了这两种噪声的存在及影响，笔者该文的结论表明这种忽略是合理的.

参考文献：

[1] ZYCZKOWSKI K, HORODECKI P, HORODECKI M, et al. Dynamics of quantum entanglement[J]. Phys Rev A, 2001, 65: 012101.

[2] ROGHANI M, HELM H, BREUEr H P. Entanglement dynamics of a strongly driven trapped atom[J]. Phys Rev Lett, 2011, 106: 040502.

[3] OLLIVIER H, ZUREK W H. Quantum discord: a measure of the quantumness of correlations[J]. Phys Rev Lett, 2001, 88: 017901.

[4] DAKI B, VEDRAL V, BRUKNER C. Necessary and sufficient condition for nonzero quantum discord[J]. Phys Rev Lett, 2010, 105: 190502.

[5] RULLI C C, SARANDY M S. Global quantum discord in multipartite systems[J]. Phys Rev A, 2011, 84: 042109.

[6] MADHOK V, DATTA A. Interpreting quantum discord through quantum state merging[J]. Phys Rev A, 2011, 83: 032323.

[7] CAVALCANTI D, AOLITA L, BOIXO S, et al. Operational interpretations of quantum discord[J]. Phys Rev A, 2011, 83: 032324.

[8] DAKIC B, LIPP Y O , MA X, et al. Quantum discord as resource for remote state preparation[J]. Nature Phys, 2012, 8: 666-670.

[9] LI B, FEI S M, WANG Z X, et al. Assisted state discrimination without entanglement[J]. Phys Rev A, 2012, 85: 022328.

[10] KNILL E，LAFLAMME R. Power of one bit of quantum information[J]. Phys Rev Lett, 1998, 81: 5672-5675.

[11] DATTA A, SHAJI A, CAVES M. Quantum discord and the power of one qubit[J]. Phys Rev Lett, 2008, 100: 050502.

[12] STRELTSOV A, KAMPERMANN H, BRU D. Behavior of quantum correlations under local noise[J]. Phys Rev Lett, 2011, 107: 170502.

[13] CICCARELLO F, GIOVANNETTI V. Local-channel-induced rise of quantum correlations in continuous variable systems[J]. Phys Rev A, 2012, 85: 022108.

[14] MAZIERO J, WERLANG T, FANCHINI F F, et al. System-reservoir dynamics of quantum and classical correlations[J]. Phys Rev A, 2010, 81: 022116.

[15] LANYON B P, BARBIERI M, ALMEIDA M P, et al. Experimental quantum computing without entanglement[J]. Phys Rev Lett, 2008, 101: 200501.

[16] XIE C M, LIU Y M, LI G F, et al. A note on quantum correlations in Werner states under two collective noises[J]. Quantum Inf Process, 2014, 13: 2713-2718.

[17] BOILEAU J C, GOTTESMAN D, LAFLAMME R, et al. Robust polarization-based quantum key distribution over a collective-noise channel[J]. Phys Rev Lett, 2004 92: 017901.

[18] ZHANG Z J. Robust multiparty quantum secret key sharing over two collective-noise channels[J]. Physica Astatistical Machanic and Its Applications， 2006, 361: 233-238.

[19] TOHYA H, SATOSHI I. Local and nonlocal properties of Werner states[J]. Phys Rev A, 2000, 62: 044302.

[20] LI G F, LIU Y M, TANG H, et al. Analytic expression of quantum correlations in qutrit Werner states undergoing local and nonlocal unitary operations[J]. Quantum Inf Process, 2015, 14: 559-572.