飞行器控制翼动特性分析

解海鸥， 郭鹏飞， 万爽， 孙兵， 张晓慧

（中国运载火箭技术研究院研发中心，北京100076）

0 引言

飞行器控制翼为飞行器产生操纵力和力矩的操纵机构[1]，是靠控制翼面在相对气流中的偏转产生操纵力，实现对飞行器俯仰、偏航和滚转的控制。控制翼作为飞行器的关键控制部件，对飞行器的飞行成败起着关键作用，而飞行器控制翼的动特性参数为控制专业提供可靠的设计依据。获得飞行器控制翼的动特性参数对飞行器可靠性设计和安全飞行具有重要的意义和参考价值，本文采用有限元软件

ANSYS Workbench对某飞行器控制翼进行了动特性分析，并与实验结果进行了比较，验证了计算模型的正确性。

1 动特性分析流程

动特性分析对于飞行器设计有重要的意义[2]，基于模态叠加法可以开展振动/噪声响应预示等结构线性动力学特性分析，用于开展颤振、气动弹性等流固耦合非线性动力学特性分析，作为飞行器弹道特性仿真分析的重要设计输入条件，用于飞行器弹道设计及稳定性分析，同时具有其它重要的用途，如频率设计与分配、结构设计缺陷及故障检查定位、结构布局及参数优化等。因此动特性分析的准确性对于飞行器研制起着至关重要的作用。

动特性分析的流程见图1所示，包括有限元分析和实

验研究两方面内容。首先经过研究绘出结构的理想模型，即通过一定假设把实际结构系统简化为一定精度的分析模型，并为分析模型赋予参数（尺寸、材料等）数据，再将分析模型化为可以计算的数学模型，采用合理的方法与程序进行动力学分析得到计算结果，通过实验来验证计算结果的正确性，最后将计算结果用于结构优化设计和飞行控制系统设计。

2 动特性分析理论

图1 动特性分析流程

动模态分析技术是现代机械产品结构动态设计和分析的基础，也是近年来迅速发展起来的系统结构动态特性分析的强有力工具。而ANSYS Workbench是用ANSYS解决实际问题的新一代软件产品，软件界面友好、使用方便，为解决工程实际问题提供了强大的功能和途径，同时也保证了很好的CAE结果，是解决实验难题较好的办法，目前使用比较广泛。动特性分析用于确定设计结构或机器部件的振动特征，即结构的固有频率和振型。

动特性分析可以确定一个结构的固有频率和振型,它们是承受动态载荷结构设计中的重要参数[3]。动特性是线性分析，任何非线性特性即使定义也将被忽略[4-5]。建立有限元系统运动方程可采用达朗贝尔原理、哈密尔顿原理、虚位移原理和最小势能原理等不同的方法。采用最小势能原理来建立有限元系统运动方程。最小势能原理指出，在给定的外力作用下，满足已知位移边界条件和协调条件的所有各组位移中，真实的一组位移应使总势能为极值。根据文献[6]中的推导可得单元的运动方程：

式中：qe为单元节点位移向量，是时间的函数（下标e表示单元）为单元质量矩阵单元阻尼矩阵为单元刚度矩阵；B为几何矩阵；N为单元位移插值函数矩阵，是空间的函数；Fe=为节点载荷向量；fe为单元内力向量；c为黏性阻尼系数；ρ为密度；D为弹性矩阵；Ω为结构上的给定体力边界；Γ为结构上的给定面力边界。

通过与单元分析相同的方法可导出运动方程为

式中：t为时间；a（t）为系统节点位移向量¨（t）和分别是系统节点的加速度向量和速度向量；M、C、K和Q（t）分别是系统的质量矩阵、阻尼矩阵、刚度矩阵和载荷向量，并分别由各自的单元矩阵和向量集成。式（2）中所有符号均为总体坐标系下的向量。

若无外力作用，可得系统自由振动方程。在实际计算中，有时考虑阻尼影响很小，可以忽略，此时便可得到无阻尼系统自由振动运动方程：

由此式可解得系统的固有频率和固有振型，所以式（3）又称为动力特性方程。

假设系统结构作如下的简谐运动：

式中：Φ是与时间无关的n阶向量；ω是振动圆频率；θ是初相位。将式（4）代入式（3），并考虑到sin（ωt+θ）的任意性，可得：

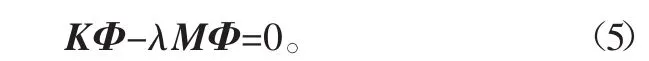
式（5）为广义特征方程，其中λ=ω2为特征值，而Φ为特征向量。其中K、M假设均为定值，因此要求材料是线弹性，使用小位移理论。同时假设无阻尼C，无激振力F。因此可知动特性分析为结构的固有频率，与外界激励无关[7-8]。

3 有限元建模

飞行器控制翼结构见图2所示，由翼面、支座、挂轴及轴承组成，对于飞行器控制翼建模而言，其动特性由4个环节组成，包括翼面、支座、挂轴、轴承。控制翼动特性分析中非线性问题突出，包括间隙、摩擦等外部因素，如何实现轴承的有效模拟是控制翼动特性建模分析的关键所在，在有限元建模中通过模拟轴承的等效刚度及质量来实现。

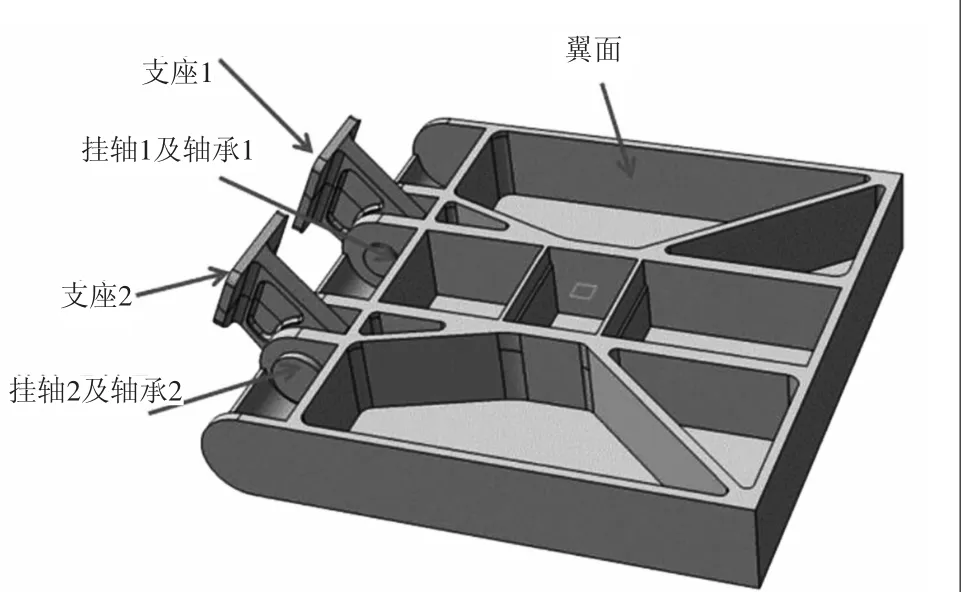
图2 飞行器控制翼结构示意

轴承的材料为钢，飞行器控制翼中其它所有部件均采用铝材料，材料参数见表1所示。

影响轴承刚度特性的因素包括轴承尺寸、轴承组合方式、轴承接触角和预紧力[9-10]，在有限元中真实建模存在困难，而且在动特性分析中也没有必要真实建模，需要等效处理。通过对轴承自身的实验测得控制翼轴承的综合刚度为3.83×108N/m，本文中采用虚拟材料层[11]对轴承进行等效模拟，虚拟材料层的几何构型、质量及刚度与轴承一致，与支座及挂轴的连接方式按接触问题计算。非线性模型能够反映出结构实际的传力路线，但其缺点是建模复杂、计算时间长，且只能进行静力学分析，无法直接进行动特性计算，因此建模过程中需将非线性结构简化为线性模型，并着重使模型能够符合结构的传力路线。在ANSYS Workbench中接触类型bonded为线性接触，因此建模中接触类型选取bonded。因此本文的计算研究中，分两步来开展，首先为虚拟材料层选取合适的弹性模量来模拟轴承的刚度，其次再建立飞行器控制翼整体的有限元模型。

表1 材料参数

通过有限元方法分析对虚拟材料层进行静力分析，通过迭代得到作用集中力1000 N，位移为2.6113 μm，得到虚拟材料的弹性模量为2.98 GPa。此时虚拟材料层的刚度与轴承刚度一致。

由于动特性分析对结构的网格要求不高，本文网格划分采用尺寸控制方法和分网方法控制[12-13]，尺寸控制方法参数通过Element Sizing选项设置，分网方法控制通过Hex Dominant来实现，运用四面体和六面体结合的方法划分，得到167 109个节点，58 489个单元。

根据控制翼的工作情况，边界条件为2个支座处固支，即分别约束6个自由度：即约束X、Y、Z三个方向的平动与转动。

4 控制翼动特性分析

有限元分析中利用Block Lanczos算法提取控制翼的振型及频率。飞行器控制翼的前3阶频率见表2所示，振型图见图3～图5所示。结果显示1阶频率80.522 Hz，远远超过舵机系统回路控制要求，可在此基础上对结构进行进一步优化，既能满足控制要求，又能实现轻质化[14]。

同时针对本文的控制翼开展了实验研究[15]，实验中通过柔性绳索给控制翼施加拉力消除机构的间隙，变化拉力值得到控制翼的动特性参数，实验结果见表3所示。由于设计中仅关注300 Hz以内控制翼的动特性参数，因此实验中仅给出了前3阶的实验结果。从计算结果与实验结果对比可知，计算结构和试验结果各阶模态振型基本一致，计算结果的频率略高，计算结果与实验结果频率最大相对偏差约9%。这是由于实验中控制翼固定在飞行器上，飞行器本身刚度低，根据GJB2076A-2008《航天器模态实验方法》可知，固定边界条件的模拟应该是支撑基础的频率应高于结构分析最高频率的5倍，而飞行器本身的频率为45.2 Hz，不满足高于控制翼分析最高频率5倍这一固支条件，不满足固支条件，而计算中的约束采用固支，约束加强，因此会提高控制翼的频率。通过计算结果与实验结果的比对，说明本文的建模方法正确可行。

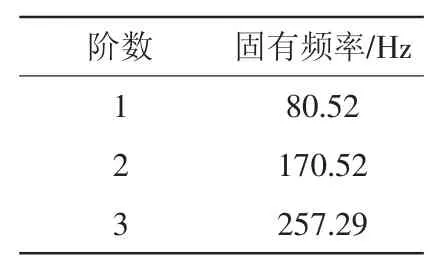
表2 飞行器控制翼前3阶频率计算结果

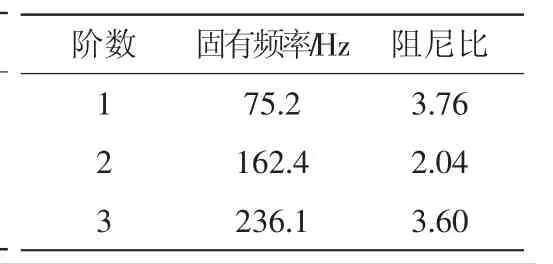
表3 飞行器控制翼前3阶频率实验结果

图3 飞行器控制翼1阶振型

图4 飞行器控制翼2阶振型

图5 飞行器控制翼3阶振型

5 结论

本文以动特性相关理论为依据，采用有限元软件ANSYS Workbench建立了飞行器控制翼的动特性模型，完成了控制翼的动特性分析，并通过计算结果与实验结果比对，证明了有限元模型的正确性，为结构优化提供了重要的参考，模型的建立为后续动力学响应分析、颤振分析等提供了重要的输入，同时分析结果为飞行控制提供重要的设计依据。

［参考文献］

[1] 龙乐豪,方心虎,刘淑贞,等.总体设计(上)[M].北京：中国宇航出版社,1993.

[2] 龙乐豪,方心虎,刘淑贞,等.总体设计(中)[M].北京：中国宇航出版社,1993.

[3] 李兵,何正嘉,陈雪峰.ANSYSWorkbench设计、仿真与优化[M].北京：清华大学出版社,2008.

[4] 张洪信,王怀敏,孟祥踪,等.ANSYS基础与实例教程[M].北京：机械工业出版社,2013.

[5] 刘赛,吴飞科,严剑刚,等.基于ANSYS边界约束条件对斜齿轮动力学模态分析的影响[J].上海第二工业大学学报,2015,32(1)：46-50.

[6] 余旭东.飞行器结构动力学[M].西安：西北工业大学出版社,2012.

[7] 王勖成.有限单元法[M].北京：清华大学出版社,2003.

[8] 凌桂龙.ANSYS Workbench13.0从入门到精通[M].北京：清华大学出版社,2012.

[9] 王硕桂,夏源明.过盈配合量和预紧力对高速角接触球轴承刚度的影响[J].中国科学技术大学学报,2006,36(12)：1314-1320.

[10] 陈宗农,董荣歌.角接触球轴承静态刚度计算[J].轴承,1993(3)：2-7.

[11] 孙丽娜,李沈,花纯利,等.柴油机曲轴连杆组合结构动态特性分析[J].东北大学学报(自然科学版),2012,33(12)：1762-1765.

[12]何军.基于ANSYS Workbench的雷达天线折叠升降机构模态分析[J].机械工程师,2015(3)：116-117.

[13] 吴腾庆,刘恒,景敏卿,等.高速电主轴支承刚度计算及模态分析[J].机械设计与制造,2013(8)：5-7.

[14] 段勇军,顾吉丰,平丽浩,等.雷达天线座模态分析与试验研究[J].机械设计与制造,2010(2)：214-216.

[15] 黄寿康.流体动力·弹道·载荷·环境[M].北京：宇航出版社,1991.