10 t桥式起重机主梁结构动态特性分析研究

刘海强， 赵坚， 洪学武， 高志鹏， 王达， 贺艺龙， 范贤安

（天津城建大学控制与机械工程学院，天津 300384）

0 引言

桥式起重机是重要的装载起重设备，广泛应用于车间、港口等场所，大大提高了生产效率[1]。主梁是桥式起重机的主要承载部分，工作时吊重的频繁起降和大、小车的频繁启动制动，极易引起主梁的剧烈振动，影响桥式起重机的吊装精度和工作效率，也对生产安全造成严重威胁[2]。在设计阶段对主梁进行模态分析获得固有频率和振型，能够有效评估结构的动态性能，再通过结构优化可以在工作频率范围避免共振[3]。

有限元法[4]解决了传统解析法设计桥式起重机主梁的局限性，能全面地对起重机主梁按实际工作的结构边界条件进行定量的分析[5]。本文使用SolidWorks软件建立了10 t桥式起重机箱型主梁的三维实体模型，利用有限元分析软件ANSYS建立有限元模型，并分别进行自由模态和约束模态分析。

1 模态分析理论

桥式起重机主梁是一个多自由度系统，视作n个单自由度系统的总和，其振动系统的运动方程为

式中：M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；f是作用力向量分别表示加速度、速度和位移列向量，其分量分别为各个自由度的广义加速度、速度和位移。

桥式起重机主梁为机械结构，其阻尼较小，可用实模态理论分析。讨论系统的固有频率和振型，先忽略阻尼和外力，其自由振动运动方程[6]为

不妨假定当系统偏离平衡位置做无阻尼自由振动时，存在一种各坐标xi作同频率ωi同相角θ的简谐振动：xi=φisin（wit+θ），代入式（2），再解系统的特征方程得到n个特征值λi及对应的特征向量φi。将n个特征向量组成矩阵：

对系统方程（2）解耦，作坐标变换：x=Φq。由特征向量的正交性有：

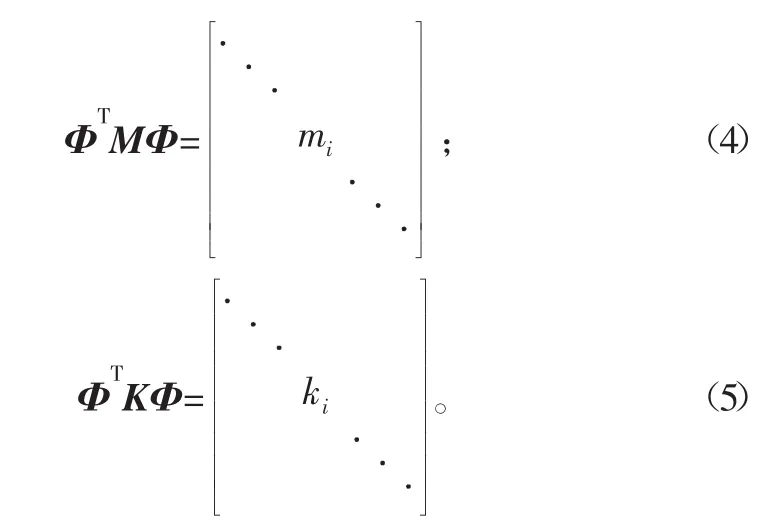
则式（2）可表示为

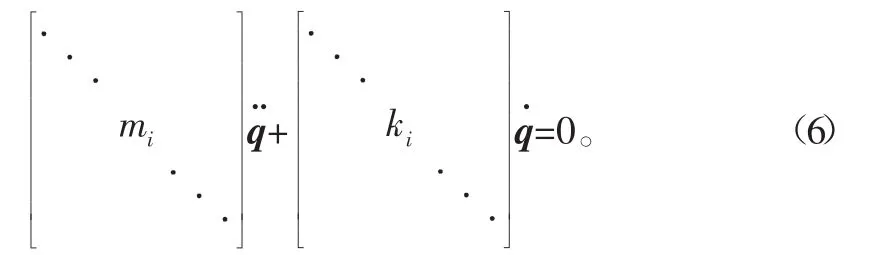
式（6）为式（2）的解耦形式。在广义坐标q下，各自由度运动方程独立：第i阶模态振动的固有频率ωi、特征值λi和模态质量mi及刚度ki存在关系：

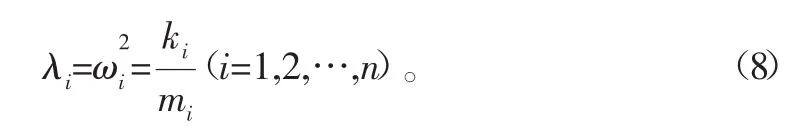
系统各自由度在作频率ωi的同相角振动时，其振幅比为第i阶固有振型。

2 主梁有限元模型

2.1 建立实体模型

本文研究的桥式起重机主梁[7]为箱型结构，它主要由上下两块盖板、左右两块腹板和若干隔板及加强筋组成。利用三维制图软件SolidWorks建立箱型主梁的实体模型，如图1所示。

图1 桥式起重机箱型主梁实体模型

其主要参数为：材料为Q235；额定起重量为10 t；跨度为22.5 m；主梁宽度为546 mm；主梁高度为1353 mm；上下盖板均为12 mm；左右腹板均为10 mm[8]。

2.2 建立有限元模型

结构的质量分布与刚度决定了固有频率和模态振型（见式（8）），为了减少有限元模态分析计算量[9]，建模时可将结构中的细小部分忽略[10]，这样不会对计算结果有较大影响。故建模时简化了主梁翼缘板伸出端梁部分的焊接板、主梁上的小车轨道和起辅助稳定作用的小加强筋及箱内纵向加强筋。

图2 桥式起重机箱型主梁有限元模型

将主梁的简化实体模型导入ANSYS，采用体单元20SOLID95进行自由智能网格划分[11]，得到单元个数为81 563，节点个数为162 656，建立的有限元模型[12-13]如图2所示。材料参数：弹性模量为206 GPa；泊松比为0.3；密度为7800 kg/m3。

3 主梁有限元模态分析

3.1 自由模态分析

桥式起重机主梁的自由模态是其自由振动的固有特性[14]，在进行自由模态有限元分析时，不考虑任何激励，也不施加任何约束。通过自由模态分析可以得到主梁各个部分振动的强弱分布，由ANSYS后处理的振型动画能直观地看到主梁的刚度薄弱区域。计算主梁的自由模态（0～100 Hz范围内），取前4阶模态[15]结果见表1，振型见图3～图6。

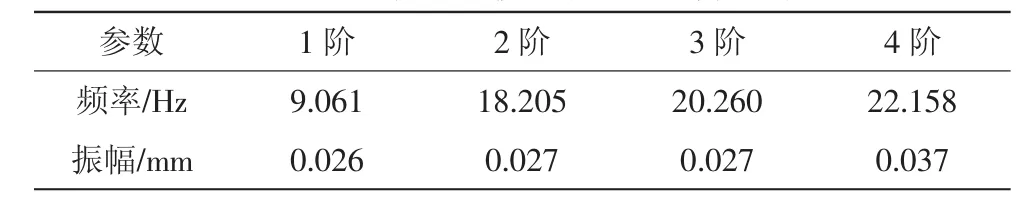
表1 主梁自由模态前4阶计算结果

图3 主梁自由模态第一阶振型

图4 主梁自由模态第二阶振型

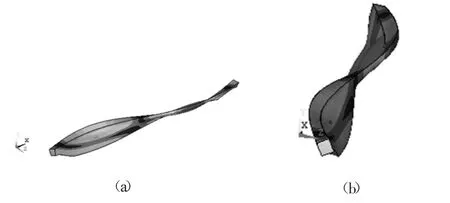
图5 主梁自由模态第三阶振型

图6 主梁自由模态第四阶振型

由主梁的各阶振型图可知：第一阶振型Z向弯曲摆动，最大变形发生在主梁两端和腹板中部，应避免小车在主梁中部时对腹板施加的水平激励；第二阶振型Y向弯曲变形，最大变形发生在主梁两端和盖板中部，应避免在主梁中部起吊对盖板施加的竖直激励；第三阶振型发生扭转变形，最大变形发生在接近主梁中部两侧的上盖板，起重机吊重运动时极易在此处产生共振；第四阶振型腹板发生水平方向变形，且变形量最大，最大振幅为0.037 mm。

3.2 约束模态分析

通过对主梁施加约束，约束模态分析反映了主梁工作时的振动状态。实际工作时，主梁两端横跨在高大的钢架或建筑上，做分析前对主梁两端施加全约束。计算主梁的约束模态（0～100 Hz范围内），取前4阶模态结果见表2，振型图见图7～图10。

表2 主梁约束模态前4阶计算结果

图7 主梁约束模态第一阶振型

图8 主梁约束模态第二阶振型

图9 主梁约束模态第三阶振型

图10 主梁约束模态第四阶振型

对比主梁的自由模态和约束模态计算结果可知：1）约束模态的固有频率整体小于自由模态的频率，且随着阶次的增加，对应阶次的频率差值逐渐减小，约束模态的第四阶频率与自由模态几乎相等。2）约束模态的各阶振型与自由模态的振型一致，在主梁两端施加约束的地方不同。3）第三阶约束模态振型的扭转变形比自由模态小，这是施加约束造成的。而且，各阶自由模态振型的主梁中部变形量在0.015 mm左右，约束模态的为0.018 mm。4）由于施加约束，主梁整体的变形量减少。

4 结语

1）施加约束后，桥式起重机主梁的频率整体向低频发展，没有出现等效刚度增加效应。这是因为约束引起主梁整体的刚度分布不均匀性增加，约束处的刚度增加而其它部位的刚度相对变差，由于主梁跨度大造成整体刚度减弱，最后导致约束模态频率比自由模态低。

2）从主梁的各阶振型可知，主梁的腹板是结构的薄弱区，可以通过结构优化提高主梁的整体振动特性。

3）在实际工作时，尽量将大车运行的水平激励避开第一阶模态频率；将起吊激励避开第二阶模态频率；将载重运行的激励避开第三阶频率。

4）运用有限元法，得到了主梁自由模态和约束模态的固有频率及对应振型，找到了结构的薄弱环节，给主梁结构的优化设计提供了数据，缩短了设计周期。

［参考文献］

[1] 张玉琴,冯山岭,张淑红.桥式起重机的动力学模型与仿真计算[J].重型机械科技,2005(3)：1-4,43.

[2] 施科益.基于经验模态分解的桥式起重机振动模态分析[J].中国特种设备安全,2014(4)：21-25.

[3] 董杰,程文明,漆静.门式起重机起升过程动态特性研究[J].机械设计与制造,2014(6)：79-83.

[4] 郗永磊,刘勇.基于ANSYS的桥式起重机结构动力学分析[J].建材世界,2017(2)：88-90,99.

[5] 程文明,李亚民,张则强.桥式起重机与门式起重机轻量化设计的关键要素[J].中国工程机械学报,2012(1)：41-49.

[6] 刘曰奇,薛伟.基于有限元的箱型桥式起重机主梁模态分析[J].森林工程,2012(2)：54-57.

[7] 杨明亮,徐格宁,常争艳,等.基于有限元法的桥式起重机桥架模态分析[J].机械科学与技术,2012(1)：135-137.

[8] 王军,杜壮,王文娜,等.基于ANSYS的桥式起重机主梁三维有限元分析[J].河北工业科技,2010(6)：361-363,377.

[9] 黄涛,王涛,杨先勇,等.桥式起重机桥架的三维有限元分析[J].武汉科技大学学报,2009(6)：623-626.

[10] 凌波,王玺,李东.基于ANSYS和数值解法的桥式起重机主梁优化方法比较[J].机械工程师,2017(1)：101-103.

[11] 刘继鹏,胡莲君,姜少伟.基于ANSYS的某种新型导轨滑块的拓扑优化[J].机械工程师,2016(8)：27-29.

[12] 焦洪宇,周奇才,李英,等.桥式起重机轻量化主梁结构模型试验研究[J].机械工程学报,2015(3)：168-174.

[13] 杨金堂,周诗洋,李公法.基于ANSYS的桥式起重机桥架结构有限元分析[J].武汉科技大学学报,2011(3)：219-222.

[14] 秦东晨,齐玉红.基于ANSYS的30t桥式起重机主梁结构优化设计[J].矿山机械,2011(5)：46-49.

[15] 赵广立,杨瑞刚,徐格宁,等.基于Pro/E三维建模的桥式起重机桥架有限元分析[J].起重运输机械,2011(1)：8-11.