双臂工业机器人设计与协调运动研究
王勇, 黄俊杰, 郑彬峰, 周际
(合肥工业大学 机械工程学院,合肥 230009)
0 引言
随着智能装备自动化技术、多传感系统信息融合技术等科学技术不断发展,机器人技术的应用领域越来越广泛[1],使用工况越来越复杂,经常需要通过两个或多个操作臂协调操作来实现单臂机器人无法完成的作业任务[2]。
双臂机器人需要两个操作臂之间的双臂协调控制[3-4],GUO Yi-shen等[5]提出了通过自适应神经网络控制双臂空间机器人系统协调运动过程中的不确定参数,Rodrigo S.Jamisola Jr.等[6]提出了针对双臂机器人的模块化、组合化设计方法。关于双臂机器人在装配过程中的应用研究方面,彭键清[7]对双臂空间机器人执行在轨装配任务中需要双臂协调操作的问题进行了研究,提出了目标捕获前及捕获后的双臂协调轨迹规划算法;魏明明等[8]将移动机器人行为动力学理论扩展到操作机器人三维空间,应用到机器人轴孔装配中,并证明了其可行性。上述方法的计算和运用过程都相对复杂,本文拟设计可分别应用于圆柱体零件的轴向约束装配和径向约束装配这两种工况下的双臂工业机器人,通过运动学、动力学仿真验证模型可行性,并分析双臂协调规划方法。
1 用于典型工况的双臂工业机器人结构设计
1.1 两种典型工况特点分析
轴向约束装配和径向约束装配是圆柱体零件典型装配,其中具有代表性的是轴孔装配和对称圆盘类装配,如图1所示。现针对这两类装配的特点进行分析,并以此来设计合适的本体机构。
轴孔装配和对称圆盘类的装配过程自动化,可通过双臂工业机器人的协调控制来实现。其中轴孔装配过程需要使两轴线在装配过程中时刻保持重合,并对两零件沿中轴线的相对运动进行控制;对称圆盘类零件的装配过程中,要保证在装配工作完成时两零件的装配部分能够完全重合。

图1 轴孔装配和对称圆盘类装配示意图
1.2 两种典型工况双臂工业机器人结构设计
这两类装配实际上都可以抽象为一维的直线运动,但考虑到实际工作中的上下料等问题,同时增加机器人的通用性,需要对其工作空间进行拓展。SCARA机器人具有结构轻便、响应快,适用于平面定位,垂直方向升降作业等特点,现基于SCARA机器人对双臂工业机器人进行本体结构设计。

图2 两种典型工况双臂工业机器人结构示意图
双臂工业机器人如图2所示,其中用于轴孔装配的工业机器人采用上下对称布置,末端分别装有吸附轴套零件的装置;用于对称圆盘类零件装配工作的双臂工业机器人左右对称布置,末端装有圆盘类零件的夹持装置。根据实际工况,将双臂工业机器人各单臂本体主要技术参数确定如表1所示。
大小臂关节处均采用了伺服电动机与减速器和推力圆柱滚子轴承相联合的驱动方式,腕部驱动方式选用电动机与同步带和滚珠丝杠配合使用来实现转动和直线升降运动。根据计算,各个关节的电动机选型如表2所示。

表1 双臂工业机器人的基本技术参数表
2 双臂工业机器人运动学与动力学分析
由于两类双臂工业机器人具有相同的单臂结构,这里以用于对称圆盘类零件装配工作的双臂工业机器人为例,对双臂工业机器人进行运动学和动力学分析,对上述的设计选型进行验证。
2.1 双臂工业机器人运动学分析

表2 关节电动机选型及其基本参数表
可建立双臂工业机器人单臂的D-H模型,各参数如表3所示。
可建立机器人基座与手爪之间的正运动变换矩阵如式(1):


表3 双臂机器人的D-H参数表
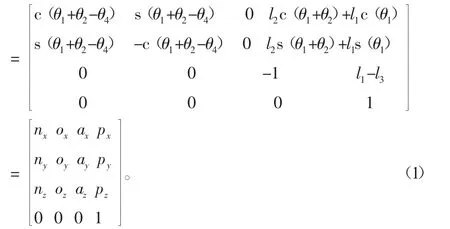
借助Matlab Robotics Toolbox工具箱建立双臂工业机器人参数模型,如图3所示,显示的是关节变量p1=[0,-pi/3,-5pi/8,-200,0],p2=[pi,pi/3,5pi/8,-100,0]时机器人的形态,其中第一个关节变量表示基座。如图3所示,得到的模型与通过正运动学公式计算得到的结果一致。
设置关节在初始和最终位置的关节变量分别为qz=[0,-pi/2,0,0,0],qr=[0,-pi/3,-5*pi/8,-100,0],其中第一个关节变量为0是为了方便建模而将双臂机器人的肩部固定,第四个关节变量表示末端执行器的竖直方向移动。采用5次多项式拟合法,仿真时间为3 s,采样间隔为0.1 s,起始点和终止点之间采样30个点,可以得到各关节角的变化情况,其中大臂关节和小臂关节角的位移、速度、加速度的变化情况如图4所示。

图3 p1=[0,-pi/3,-5pi/8,-200,0],p2=[pi,pi/3,5pi/8,-100,0]时机器人形态图
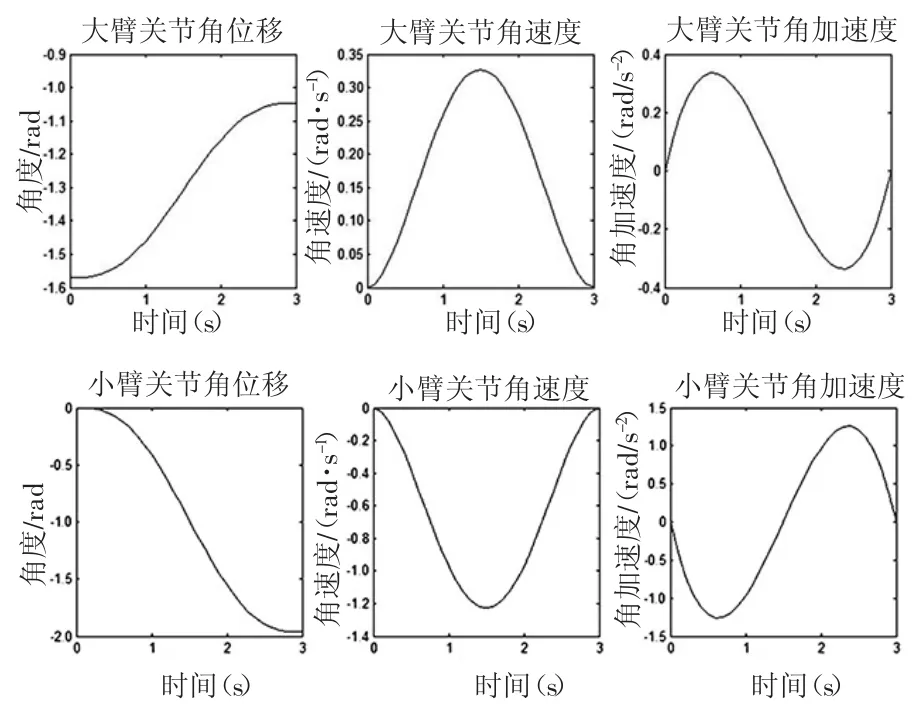
图4 大、小臂关节角位移、角速度、角加速度变化
得到的机器人大小臂关节角的变化曲线都是连续、平稳、光滑的,没有出现突变情况,无明显的冲击和振动,保证双臂机器人运动的平稳性。
2.2 双臂工业机器人动力学仿真
将得出的大臂和小臂关节位移变化的数据离散点导入到ADAMS中,作为大臂和小臂关节的驱动,用于对双臂机器人进行动力学仿真分析。将载荷和驱动定义好之后,将仿真时间设置为3 s,仿真步数设置为5000。得到大臂关节和小臂关节的驱动力矩变化如图5所示。

图5 大、小臂铰接点处力矩大小变化
可以看出曲线平滑,没有出现较大波动,满足稳定性要求;大、小臂关节处所受最大力矩分别为为361.26 N·mm和613 N·mm,均小于电动机额定转矩1270 N·mm,满足使用要求。
由运动学和动力学分析结果,可知本文设计的双臂工业机器人本体结构设计合理可行。
3 两种典型工况下双臂工业机器人运动规划方法
根据运动特点,双臂工业机器人本体结构只有竖直方向上的平移运动和旋转运动,运用投影法将机器人转换成二维数学模型,以下分别对双臂工业机器人的协调运动规划方法进行说明。
3.1 轴孔装配双臂工业机器人运动规划方法
如图6所示,装配过程中的轴、孔零部件轴线始终平行,不需要对机器人末端位姿的协调计算工作。ABC与A′B′C′分别是左臂与右臂的初始位置,o为AA′中点。α、α′分别AB、A′B′与x轴的夹角,β、β′分别AB与BC,A′B′与B′C′的夹角。设OA=OA′=a,AB=A′B′=b,BC=B′C′=c,则有:A点坐标(xA,yA),B点坐标(xB,yB),C点坐标(xC,yC),有:

图6 用于轴孔装配的双臂工业机器人运动规划示意图

这里若通过C点坐标直接求解α、β,会出现2个解,因此可先通过B点坐标确定α的值,再根据C点坐标求β的值。当左臂末端执行器移动至设定的D(xD,yD)处时,左臂处于AB1C1位置。根据式(2),同理对D点的坐标有:

式(3)中,α1、β1为未知量,求解过程中会有2组解,这里可通过比较的值,选取较小的那组作为需要的解。左臂运动过程即大臂转角α→α1,小臂转角β→β1。当两臂末端投影移动到同一位置时,轴、套零件中轴线重合,通过腕部升降、旋转两关节配合运动,可完成装配任务。右臂同理。
3.2 对称圆盘类装配双臂工业机器人运动规划方法
如图7所示,ABC与A′B′C′分别是左臂与右臂初始位置,左臂与右臂沿中轴线对称,因此有α=α′=β=β′,且BC和B′C′沿中轴线对称;CD和C′D′分别表示夹持装置,保持夹持装置方向与小臂平行并固定。根据零件尺寸,可计算得到各关节所需转动的θ角。若左右大臂、小臂运动规律相同,设为θ(t),则有:α+θ(t)= β+θ(t)=α′+θ(t)=β′+θ(t),即BC与B′C′时刻都保持平行且沿中轴线对称,同时末端执行器也能保证对齐,保证了待装配两零件也能够对齐。由于对称圆盘这种特殊形状,装配过程中两零件不会发生碰撞。

图7 用于对称圆盘类装配的双臂工业机器人运动规划示意图
4 结论
本文针对圆柱体零件的轴向约束和径向约束这2种典型装配工况下的双臂机器人分别提出了可行方案,基于SCARA机器人设计出简单可行的本体结构,避免了对双臂协调、避障等方面所要做的大量计算工作,提高了双臂机器人的实用性和可操作性,也为双臂工业机器人应用于径向与轴向约束装配时的协调运动控制方法研究提供了新的思路。
[参 考 文 献]
[1] 王东署,朱训林.工业机器人技术与应用[M].北京:中国电力出版社,2016.
[2] 赵京.冗余度机器人、弹性关节冗余度机器人及其协调操作的运动学和动力学研究[D].北京:北京工业大学,1997.
[3] ZHENG Y F,LUH J Y S.Optimal load distribution for two industrial robots handling a single object[C]//IEEE International Conference on Robotics and Automation.1988:344-349.
[4] LEE S.Dual redundant arm configuration optimization with task-oriented dual arm manipulability[J].IEEE Transactions on Robotics&Automation,1989,5(1):78-97.
[5] GUO Yishen,CHEN Li.Adaptive neural network control for coordinated motion of a dual-arm space robot system with uncertain parameters[J].Applied Mathematics and Mechanics,2008,29(9):1131-1140.
[6] JAMISOLA R S JR,KORMUSHEV P S,ROBERTS R G,et al.Task-Space Modular Dynamics for Dual-Arms Expressed through a Relative Jacobian[J].Journal of Intelligent&Robotic Systems,2016,83(2):205-218.
[7] 彭键清.双臂空间机器人捕获与操作目标的协调控制研究[D].哈尔滨:哈尔滨工业大学,2014.
[8] 魏明明,傅卫平,蒋家婷,等.操作机器人轴孔装配的行为动力学控制策略[J].机械工程学报,2015,51(5):14-21.

