RV减速器的运动学研究

赵盛， 段素爽， 赵利锋

（国机智能技术研究院有限公司，北京 100083）

0 引言

RV(Rotary Vector)减速器是一种在关节型工业机器人上被广泛用作关节减速器的精密减速器，具有体积小、重量轻、寿命长、精度高、刚度大、传动比范围大、传动效率高等一系列优点[1]9-126，在全球的工业机器人关节减速器市场上占有约60%的市场份额。RV减速器由两个行星传动部分构成，这两部分不是串联或并联，而是构成封闭差动轮系[2]181。对RV减速器的运动原理，目前还缺乏专门

的论述。一些文献给出了RV减速器的传动比计算公式[3-4]，但推导方法理论性强、不直观，且只涉及一种安装方式下的传动比。对RV减速器中各运动件的运动关系，尤其是影响受力分析的运动关系，尚无阐述。本文从RV减速器的构成、运动传递过程以及各构成部分的运动原理等方面，对RV减速器的运动原理进行了分析；直观地推导了RV减速器在各种安装方式下的传动比的计算公式；总结了RV减速器各运动件的运动关系，尤其是对与受力分析相关的运动关系做了说明。本文有助于相关研究人员理解RV减速器的运动原理、传动比计算公式以及各运动件的运动关系，进而在受力分析过程中将运动件的运动状况纳入考虑，从而使受力分析结果更符合实际。

1 RV减速器的运动原理

RV减速器的运动原理，主要包括RV减速器的构成、运动传递过程以及各构成部分的运动原理。

1.1 RV减速器的构成及运动传递

图1是RV减速器的机构运动简图[5]，借此可以说明RV减速器的构成及运动传递过程。

如图1所示，针齿壳固定作为机架，输入齿轮与行星轮相啮合并作为输入轴，行星轮与曲轴固联，曲轴的非偏心段通过回转副支承于行星架上，曲轴的偏心段通过回转副支承摆线轮，摆线轮与针齿相互啮合，针齿通过回转副支承于针齿壳内，行星架通过回转副支承于针齿壳内并作为输出轴。

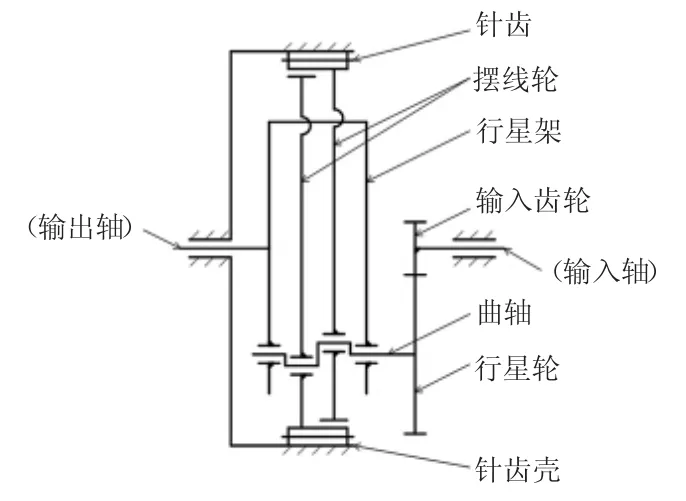
图1 RV减速器的机构运动简图

行星架位于摆线轮的两侧，在摆线轮上开有孔，供行星架穿过摆线轮。图1借鉴了电路图中交叉线的画法，使用半圆弧表示行星架穿过摆线轮。

下面分析RV减速器的运动传递过程。为简化分析，以针齿壳轴心为坐标原点建立机架坐标系OXY，如图2所示。

RV减速器是一个封闭差动轮系。其中，差动轮系部分由输入齿轮、行星轮以及行星架构成；封闭部分是一个摆线针轮行星传动机构，由曲轴、摆线轮、针齿以及针齿壳构成；两部分之间，行星轮与曲轴固联，行星架、曲轴与摆线轮构成等角速传动机构。差动轮系部分的自由度为2，封闭部分通过两部分之间的连接关系对差动轮系部分进行封闭，减少了1个自由度，从而构成自由度为1的RV减速器。

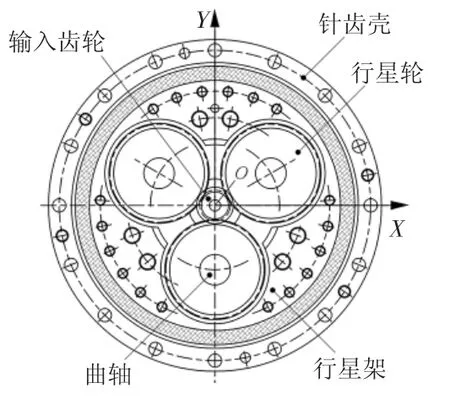
图2 机架坐标系

在RV减速器中，行星轮、曲轴和摆线轮均做行星运动，三者既自转又公转。本文约定：自转是运动件相对于自身轴线的转动，因此自转角速度就是运动件的绝对角速度；公转是运动件轴心（运动件轴线在图2中的投影点）相对于机架坐标系原点O的转动，因此公转角速度就是运动件的牵连角速度。公转角速度实际上也就是运动件系杆（连接机架坐标系原点O和运动件轴心的真实杆件或虚拟杆件）的角速度。根据角速度合成定理[6]，运动件相对于其系杆转动的相对角速度就等于其绝对角速度（自转角速度）减去牵连角速度（公转角速度）。

当RV减速器的输入齿轮转动时，行星轮与输入齿轮啮合而自转，但行星轮的公转处于自由状态。行星轮的自转带动曲轴自转，从而使摆线轮发生公转。摆线轮在公转时，与针齿啮合而发生自转。摆线轮的自转通过曲轴传递给行星架。行星架的转动带动曲轴和行星轮公转，从而使整个机构实现具有一定角速度关系的确定运动。

接下来，分别说明RV减速器三个主要构成部分——差动轮系部分、封闭部分以及等角速传动机构的运动原理。

1.2 差动轮系部分的系杆

差动轮系部分由输入齿轮、行星轮以及行星架构成。连接机架原点O和行星轮轴心的虚拟杆件，其转动速度与行星架的转动速度一致，因此行星架是行星轮的系杆。

1．3 封闭部分的系杆

封闭部分是一个摆线针轮行星传动机构，由曲轴、摆线轮、针齿以及针齿壳构成。连接机架原点O和摆线轮轴心Oc的虚拟杆件，其转动速度与曲轴的自转角速度一致，因此可以认为曲轴是摆线轮的系杆。解释如下：RV减速器通常有2～3个曲轴（图2所示的RV减速器有3个曲轴）。曲轴既做自转，又做公转。定义曲轴的轴心为其非偏心段的轴线在图2中的投影点，则如图3所示，各曲轴的轴心H、I、J组成一个正三角形，此正三角形的中心与机架原点O重合；各曲轴偏心段的中心（也即摆线轮上安装曲轴偏心段的孔的中心）A、B、C也组成一个正三角形，此正三角形的中心与摆线轮的轴心Oc重合。因此，摆线轮轴心Oc相对于机架原点O的转动角速度，就等于曲轴偏心段中心相对于曲轴轴心的转动角速度，也即曲轴的自转角速度。

1．4 等角速传动机构

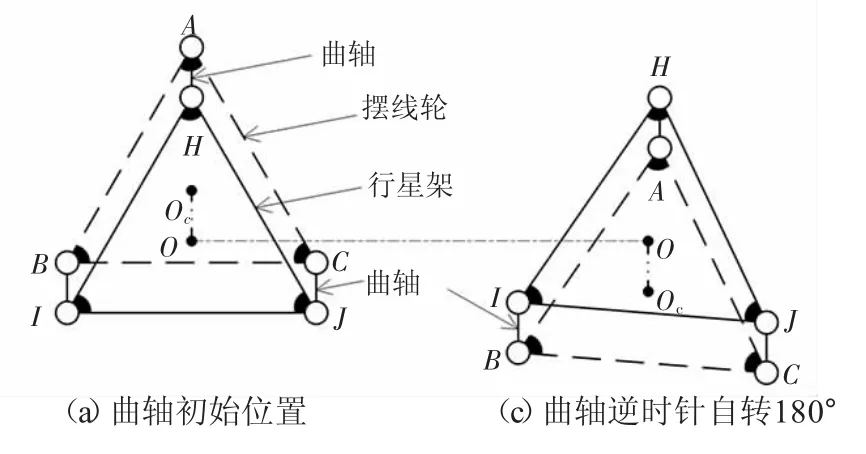
图3 行星架、曲轴及摆线轮的运动简图

行星架、曲轴与摆线轮构成等角速传动机构，其运动简图如图3(a)所示。该机构使行星架的角速度等于摆线轮的自转角速度，说明如下。

如图3(a)所示，AH与BI大小相等且在运动过程中保持平行，故四边形ABIH为平行四边形（有时候该四边形退化成线段，但不影响此处的推理过程），所以摆线轮的AB与行星架的HI在运动过程中将始终保持平行。因此，摆线轮将始终与行星架等速同向转动[2]211。

2 RV减速器的传动比

在分析了RV减速器的运动原理后，可以推导出其传动比。当RV减速器的安装方式不同时，其固定端、输入端、输出端不局限于前述针齿壳固定、输入齿轮输入、行星架输出的安装方式。本节将通过分析RV减速器各构成部分的传动比，来获得RV减速器在各种安装方式下的传动比。

2.1 差动轮系部分的传动比

在差动轮系部分，行星架为系杆H′，输入齿轮为轮1，行星轮为轮2，轮1与轮2为外啮合，因此其转化机构的传动比为

式中：ω1为输入齿轮的角速度；ω2为行星轮的自转角速度（也即绝对角速度，下文不再赘述）；ωH′为行星架的角速度；z1为输入齿轮的齿数；z2为行星轮的齿数。

2.2 封闭部分的传动比

封闭部分是一个摆线针轮行星传动机构，其中，曲轴为系杆H″，摆线轮为轮3，针齿壳及针齿组成的针轮为轮4，轮3与轮4为内啮合，因此其转化机构的传动比为：

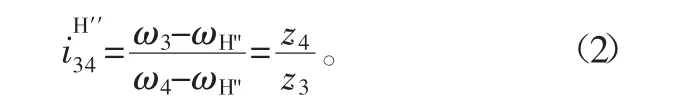
式中：ω3为摆线轮的自转角速度；ω4为针轮（或针齿壳）的角速度；ωH"为曲轴的自转角速度；z3为摆线轮的齿数；z4为针轮的齿数，也即针齿的个数。在RV减速器中，z4=z3+1。

2.3 两部分之间的传动比

行星轮与曲轴通过花键固联，因此有：

行星架、曲轴与摆线轮通过等角速传动机构连接，因此有：

2.4 RV减速器传动比的计算式

联立式(1)～式(4)，并将固定端的角速度用0代入，就可得出RV减速器在各种安装方式下的传动比。

2.4.1 针齿壳固定、输入齿轮输入、行星架输出

此时针齿壳的角速度ω4=0，RV减速器的传动比为

式中，i1H′的符号为正，说明输入齿轮与行星架的角速度方向相同。

2.4.2 行星架固定、输入齿轮输入、针齿壳输出

此时行星架的角速度ωH′＝0，RV减速器的传动比为

式中，i14的符号为负，说明针齿壳与输入齿轮的角速度方向相反。

2.4.3 输入齿轮固定、针齿壳输入、行星架输出

此时输入齿轮的角速度ω1=0，RV减速器的传动比为

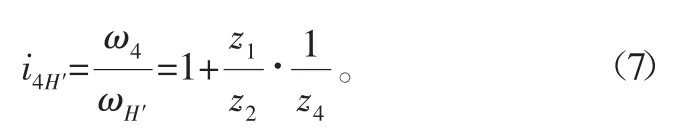
式中，i4H′的符号为正，说明针齿壳与行星架的角速度方向相同。

以RV-320E-201减速器为例，z1=14，z2=70，z4=40，所以其各种安装方式下的传动比分别为i4H′=201，i14=-200，i4H′=1.005。

3 RV减速器的运动学

基于上述分析，可以得出RV减速器各运动件的运动关系。本节以针齿壳固定、输入齿轮输入、行星架输出的安装方式为例进行说明，其他安装方式可类似进行分析。

3．1 RV减速器各运动件的运动关系

联立式（1）～式（4），令针齿壳的角速度ω4=0，则可得RV减速器在输入齿轮以角速度ω1转动时各运动件的运动关系，如表1所示。

表1 RV减速器各运动件的运动关系

从表1可知，当输入齿轮逆时针转动时，行星轮顺时针自转并逆时针公转，曲轴与行星轮相同，摆线轮逆时针自转并顺时针公转，行星架逆时针转动。摆线轮的自转角速度等于行星架的角速度，等于行星轮或曲轴的公转角速度；摆线轮的公转角速度等于行星轮或曲轴的自转角速度。行星轮的自转角速度等于行星轮公转角速度的-z3倍，这正是封闭部分对差动轮系部分所增加的约束，即：行星轮自转和公转的未定角速度关系，通过固联和等角速传动机构连接，转化成摆线针轮行星传动机构中曲轴自转和摆线轮自转的确定角速度关系。

从表1还可得出，曲轴与摆线轮之间向心滚针和保持架组件的等效内外圈的相对转速为ω2-ω3=-（ω1/i1H′）·z4，曲轴与行星架之间圆锥滚子轴承的内外圈的相对转速为ω2-ωH′=-（ω1/i1H′）·z4。

表2 RV-320E-201减速器各运动件的运动关系 r/min

以RV-320E-201减速器为例，i1H′=201，z3=39，z4=40，其各运动件的运动关系如表2所示（使用转速表示）。其向心滚针和保持架组件的等效内外圈的相对转速为-40 r/min，圆锥滚子轴承的内外圈的相对转速也为-40 r/min。

3.2 摆线轮和针轮啮合节点的运动

摆线轮和针轮的啮合节点P是摆线轮和针齿相互作用力的作用线上的点，对受力分析具有重要意义。下面对节点P的运动加以说明，以供受力分析时参考。

根据摆线轮和针轮的啮合原理[1]9-84，摆线轮和针轮的啮合节点P位于针轮（或针齿壳）轴心O和摆线轮轴心Oc的连线上，。因此，节点P相对于机架原点O的转动角速度，就等于摆线轮轴心Oc相对于机架原点O的转动角速度，即摆线轮的公转角速度（或曲轴的自转角速度，见图3）。基于此，由表1即可得出节点P相对于机架原点O转动角度θ时各运动件的转动角度，如表3所示。

表3 节点P转动角度与运动件转动角度的关系

从表3还可得出，节点P转动角度θ时，曲轴相对于摆线轮的转动角度为θ－（-θ/z3）=（θ/z3）·z4，节点P相对于摆线轮的转动角度为θ－（-θ/z3）=（θ/z3）·z4。

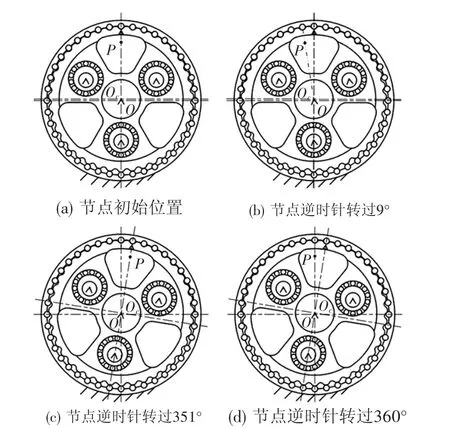
图4 RV-320E-201减速器摆线轮和针轮啮合节点P的运动

下面以RV-320E-201减速器为例对节点P的运动进行说明，其中i1H′=201，z3=39，z4=40。如图4所示，在摆线轮上设置一个三角形标记，在曲轴轴心到曲轴偏心段中心设置一个箭头，在机架原点O到摆线轮轴心Oc设置同样的箭头。

根据摆线轮和针轮的啮合原理[1]9-84，当针齿的轴心落在直线OOc（也即直线OP）上时，该针齿及其所在的摆线轮齿槽可关于同一条直线对称，称二者处于对称位置，如图4中直线OP上的针齿及摆线轮齿槽；其他针齿和其所在的摆线轮齿槽不处于对称位置。

在图4(a)中，直线OOc竖直，节点P正上方的摆线轮齿槽（以三角形标记）和针齿处于对称位置，以此为初始位置。如图4(b)所示，当节点P逆时针转过9°时，根据表3，摆线轮公转9°，曲轴自转9°，摆线轮自转仅约-0.23°，直线OP上的摆线轮齿槽和针齿处于对称位置。在图4(c)中，当节点P逆时针转过351°时，摆线轮公转351°，曲轴自转351°，摆线轮自转-9°，直线OP上的摆线轮齿槽和针齿处于对称位置。可见，节点P逆时针每转动9°（也即曲轴逆时针每自转9°）时，摆线轮的齿槽从图4(a)开始，逆时针逐个和对应针齿进入对称位置，直至节点P转动351°（也即曲轴自转351°）时，处于对称位置的摆线轮齿槽完成一个周期，此时曲轴相对于摆线轮转过360°。在图4(d)中，当节点P逆时针转过360°时，摆线轮公转360°，曲轴自转360°，摆线轮自转约-9.23°，直线OP上的摆线轮齿槽和针齿处于对称位置，处于对称位置的针齿完成一个周期，此时曲轴相对于摆线轮转过约369.23°。

4 结 论

本文分析了RV减速器的运动原理。RV减速器是一个封闭差动轮系，由差动轮系部分和封闭部分两部分构成。差动轮系的自由度是2，封闭部分给差动轮系部分增加了1个约束，二者构成自由度为1的RV减速器。差动轮系部分是一个渐开线齿轮行星传动机构，行星架为其系杆。封闭部分是一个摆线针轮行星传动机构，曲轴为其系杆。差动轮系部分和封闭部分之间有两处连接，分别是行星轮和曲轴之间的固联以及行星架和摆线轮之间的等角速传动机构连接。通过这两处连接，行星轮和行星架之间未定的运动关系转化成曲轴和摆线轮之间确定的运动关系。

在使用转化机构法分析了差动轮系部分和封闭部分各自的传动比之后，推导出了RV减速器在各种安装方式下的传动比计算公式。同时，得出了RV减速器中各运动件的运动关系。由于摆线轮和针轮的啮合节点在受力分析中具有重要意义，因此对节点P的运动情况进行了特别说明。本文可供相关研究人员理解RV减速器的运动学,掌握其各种安装方式下的传动比的计算方法,明确其运动件的运动关系，尤其是对受力分析有一定参考价值的摆线轮和针轮的啮合节点的运动情况。

[参 考 文 献]

[1] 闻邦椿.机械设计手册：第2卷[M].5版.北京：机械工业出版社,2010.

[2] 申永胜.机械原理教程[M].2版.北京：清华大学出版社,2005.

[3] 饶振纲.行星传动机构设计[M].2版.北京：国防工业出版社,1994：432-433.

[4] 陈姗姗.工业机器人关节用RV减速器运动学分析及关键零部件制造工艺探索[D].宁夏：宁夏大学,2015：8.

[5] 摆线针轮行星传动第2部分：图示方法：GB/T 10107.2-2012[S].

[6] 李俊峰.理论力学[M].北京：清华大学出版社,2001：45-46.