用纸片折出特殊的多边形

毛亚玲 郝四柱

同学们，我们都会折纸.那么如何用一张纸片折出平行四边形呢？

下面，让我们一起进入“做”数学的天地.

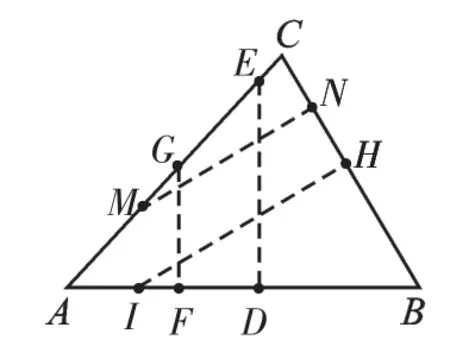
图1

图2

活动1：给出一个任意的三角形或者四边形纸片，你能折出平行四边形吗？首先你能折出两条平行的线吗？如图1，使AB边对折两次（第一次使得A与B重合，然后再对折一次），得到的两个折痕（DE和FG）就是一组平行线.同理，用四边形纸片折也是如此.

其实，不需要对折也是可以的.只要折后点A落在AB所在的直线上，那么得到的折痕就平分了AB边所在的平角，得到两个相等的角.同样，再按相同原理折一次就得到了一组平行线.

如图1，在得到一组平行线后，只需要再将三角形的另一条边BC对折两次，再得到一组平行线（IH和MN），则这两组平行线围成的图形即为所求的平行四边形.同理，用四边形纸片折也是如此.

活动2：在不规则的纸片中折出平行四边形.

由活动1的经验，只要折出两组相交的平行线即可.

图3

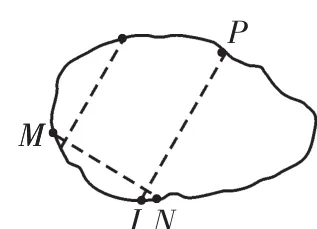
图4

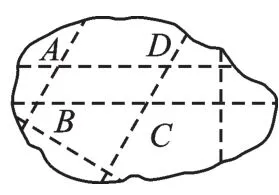
图5

第一步：如图4，在不规则的纸片中折一道折痕MN，以此为边，视这条边为平角，折两次，均使得平角的边重合，即得到一组平行线.

第二步：重复第一步操作得到第二组平行线.两组平行线相交得到平行四边形ABCD.

活动3：在不规则的纸片中折出矩形.

如图6，在活动2第一步的基础上，只要再折出折痕MN的平行线即可.将折痕IP视为平角，折一次使得I落在平角的边上，再将纸片沿着MN折一次，得到折痕EF，此时便得到了矩形GHWX.

图6

图7

活动4：在不规则的纸片中折出菱形.

在活动2的基础上，构造平行四边形的一组邻边相等即可得到菱形.

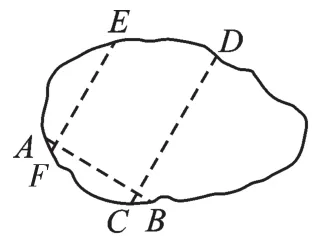
图8

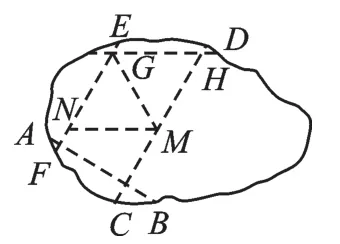
图9

第一步：如图8，在活动2的基础上先折出两条平行线CD和EF.

第二步：如图9，任意折一道折痕GH，使得GH与两条平行线CD、EF分别相交于G、H.

第三步：如图9，以G为顶点，使得GH与EF边重合，得到折痕GM，并且GM交CD于M.接着，沿着HM再折一次便得到了点N.则四边形GHMN即为所求的菱形.

活动5：在不规则的纸片中折出正方形.

在活动2的基础上，只要使得矩形的邻边相等即可.

图10

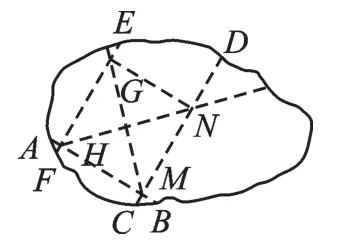
图11

第一步：如图10，由活动2先得出一组垂直于AB的平行线CD与EF，设CD与EF分别交AB于M、H.

第二步：如图11，以H为顶点，使得HM与HE重合，得到折痕HN.过N点折GH的垂线NG即可得到正方形.

活动6：利用平行线先折出等边三角形，再折出正六边形.

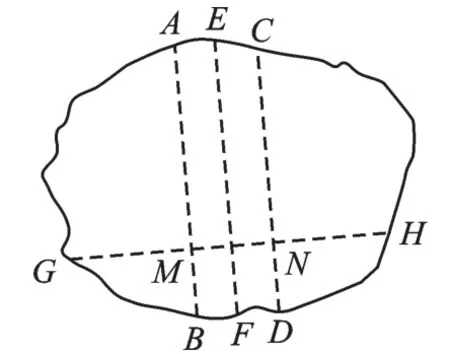
图12

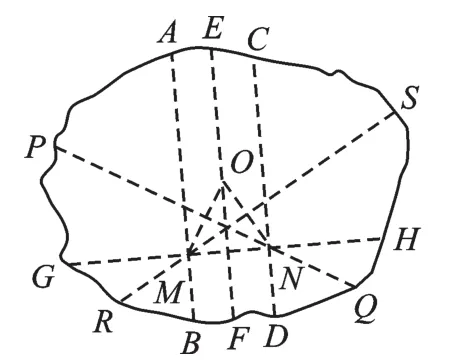
图13

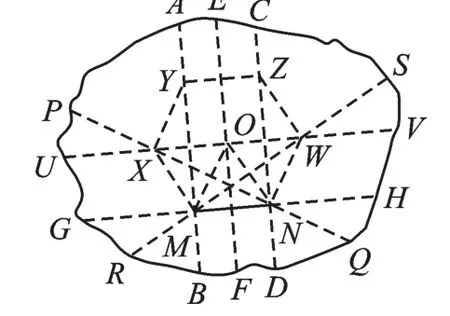
图1414

第一步：如图12，利用前面的活动经验，先折出两条平行线AB与CD，再对折，使得AB与CD所在折痕重合，得到折痕EF.设GH与AB、CD相交于M、N.

第二步：如图13，过M点将MN向上翻折，使得N点落在EF上，得到折痕RS和点O，同理得到折痕PQ.

第三步：如图14，过O点折出GH的平行线UV，则UV交折痕PQ、RS于X、W.

第四步：沿着UV将纸片对折，再将纸片沿MN折一次，得到折痕YZ，此时YZ与AB、CD分别相交于Y、Z.由此得到正六边形MNWZYX.

同学们，对于活动5和活动6，你知道为什么这么折吗？